悬浮水轮回复现象的探究
2021-08-19沈君宇姚关心
沈君宇,陈 鑫,姚关心
(安徽师范大学 物理与电子信息学院, 安徽 芜湖 241002)
2019年全国大学生物理学术竞赛中提出了这样一个探究性问题:在靠近水柱的边缘小心地朝上放置一个轻质物体,如聚苯乙烯泡沫塑料盘(称悬浮水轮),在一定条件下,物体将在悬浮的同时开始旋转.文献上对这种现象的解释有不少报道[1-3],本文将利用流体力学中的边界层理论与康达效应对这一现象进行研究,并对它随水柱冲击点变化产生的回复现象作出合理的解释.
1 预实验猜想
轻质聚乙烯球会在水柱侧边稳定高度悬浮并快速旋转;旋转过程中水流会沿其表面运动并泼洒出大量水花.通过预实验,可以作出稳定时轻质物体受力平衡的条件与水柱冲击点位置有关的判断.
2 悬转水轮的力学模型
2.1 水轮旋转的原因
根据康达效应可以知道:1)流体(水流或气流)有偏离原本流动方向,改为随凸出的物体表面流动的倾向;2)当流体与它流过的物体表面之间存在表面摩擦时(即流体粘性),只要曲率不大,流体会沿该物体表面流动; 3)据牛顿第三定律,物体施与流体一个偏转的力,流体也必施与物体一个反向偏转的力.这种力在轻质物体表面动力学过程非常明显,这种力产生的力矩会使轻质物体旋转起来.
2.2 力学模型构建
如图1所示的x-y系中,将沿水轮表面水流速度分解为法向vcosθ与切向vsinθ.

图1 悬转水轮表面速度分量与受力示意图
现对轻质物体做受力分析
G=mg
(1)
如图1,水流在dt时间内对球体的冲击导致其沿球体法向动量变为0而只沿球体表面切向运动,由动量定理此法向冲击力P满足
Pdt=vcosθdm
(2)
沿球体切向运动的水流会对球体产生黏滞阻力[4],即流体流经物体表面产生的沿切向的湿摩擦力R[5]:
R∝v2cos2θ
(3)
当水流速度小于球体线速度时,同理会在球体表面产生反向的黏滞阻力Q:
Q∝v2sin2θ
(4)
水轮在这4种力及其产生的力矩的作用下最终达到平衡 .
在dt时间内,v=Const,喷出水柱高度及喷出水柱质量分别为
dl=vdt
(5)
dm=ρdV
(6)
其中
dV=Sdl
(7)
冲击点法向单位时间内喷出的水的质量可写为
dm/dt=ρSvcosθ
(8)
代入式(2)可得
P=ρSv2cos2θ(>cosθj-sinθi)
(9)
因为R、Q两力的大小正比于水流的切向速度的平方,故其两者合力大小必正比于水流切向速度的平方,即
R,Q∝v2sin2θ→FR,Q∝v2sin2θ
(10)
由于球体受力平衡,此模型下两种力矢量和FR,Q的方向指向第一象限,假设其与x轴夹角同为θ,由边界层理论[6]知
(11)
其中,CD为阻力系数,Re为雷诺数,S为流体喷射截面面积,且其满足如下式子[7-8]
(12)
其中,ρ为流体密度,ω为球体旋转角速度,μ为流体动力黏度,r为流体喷射截面半径.由此,水轮在水平方向上所受外力矢量和可写成

(13)
2.3 稳定性的研究
实验中观察到:对于同一球体,在达到稳定悬浮后,冲击点总是在偏离球心的固定位置;当冲击点稍偏离平衡位置时,球都会受到水施加的“回复力”,将之拉回平衡位置.利用式(13),并以式中角度为横坐标、水平合力大小为纵坐标绘制成的图像配合探究此平衡点的位置并解释这一现象.
当水平方向外力为0,有
(14)
当sinθcosθ≠0时,有
当sinθcosθ=0时,有
即水柱冲击点在θ角度满足以下条件时,水轮所受横向合外力为零
水柱沿竖直方向冲击球体时:θ3=0

表1 实验中相关系数测量记录表
3 实验数据结果及分析
固定喷水口喷射截面积不变,形状为半径r为0.3 cm的圆形,并假设水柱上升过程中不会散开;黏度μ取室温值:1.01×10-3Pa·s.通过对不同尺寸的水轮进行悬浮实验,测量式(11)、(12)中给出的其余相关物理量(见表1),取g=10 m/s2,将所得CD值带入(14)中,以式(14)中角度为横坐标、水平合力大小为纵坐标利用软件绘制不同实验参数下两者之间的图像关系(见图2—图4),即经过数值计算得到的理论上水平合力与冲击角度之间的关系.设R0为球体半径.
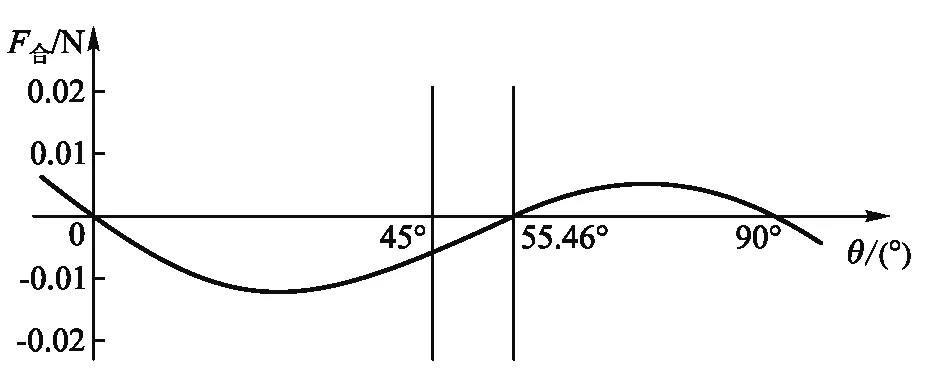
图2 角度θ与水平合力F合的关系(2R0=8 cm)

图3 角度θ与水平合力F合的关系(2R0=10 cm)

图4 角度θ与水平合力F合的关系(2R0=12 cm)
由图2—图4可解释“回复力”现象产生的原因即由水平分力的合力产生,即是当冲击水柱的位置右移时,轻质球体将会受到水流产生的向左的水平合力;当冲击水柱的位置左移时,轻质球体将会受到水流产生的向右的水平合力.
4 结论
通过上述理论分析和实验数据结果表明:
1) 水轮稳定悬浮的条件是由重力G,冲击力P,黏滞力R,水的反向黏滞阻力Q的共同作用下达到受力平衡;在黏滞力R与水的反向黏滞阻力Q产生的力矩作用下达到力矩平衡.

3) 由(13)知,在水柱冲击点偏移时,水轮会受到类似“回复力”的作用是P、Q、R3种力的水平合力共同作用产生,平衡位置与竖直方向所夹圆心角受流体速度,冲击面积等条件影响.
