麦克斯韦-玻尔兹曼分布在易辛模型中的应用

应 涛，裴延波，王晓鸥，张 宇

(哈尔滨工业大学 物理学院，黑龙江 哈尔滨 150001)

在统计物理的教学中，麦克斯韦-玻尔兹曼统计是一个重点内容. 但这部分的内容比较抽象，学生学习的时候往往是一知半解，需要有更多实例来给学生讲解，特别是联系到我们现实生活的关于麦克斯韦-玻尔兹曼应用的实例.

我们生活在一个丰富多彩的世界里，身边的万事万物各有各的特点，比如水是柔软流动的，石头是坚硬的等等.但是从微观的角度来看，这些各式各样的宏观物体都是由大量的微观粒子构成的，这些微观粒子的无规则热运动导致了宏观物体的不同特性.也就是说，为了了解宏观物体特性出现的原因，我们需要从这个宏观物体的微观构成来进行研究.对单个的微观粒子来说，它的个体行为是无规律的，难以捉摸的.但是大量的微观粒子一起则会遵循统计规律，而这个统计规律在宏观上就表现出实际物体的特征[1-4].

1 统计物理中的麦克斯韦-玻尔兹曼分布

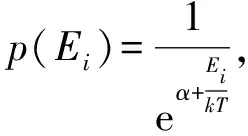
在平衡态统计物理中，我们通常考虑处于某一个环境中的平衡系统，该系统的能量并不是精确固定的，因为它是在不断的和外界环境进行能量的交换，因此这个系统的微观状态也不是固定的.根据等概率假设，系统有一定的概率处于任意的一个微观状态|n〉，而该概率就是归一化后的玻尔兹曼分布

(1)

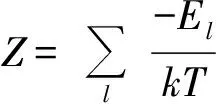
我们在实际中观测到的宏观物理量都是对应微观量的统计平均值，但是进行这些统计平均时需要考虑到系统处于不同状态的玻尔兹曼概率，也就是进行加权平均.对某个观测量A(比如系统能量)而言，我们观察到的统计平均值可以表达为

(2)

其中An表示观测量A处于状态|n〉时的值.根据公式(2)，系统的平均能量可以表示为

(3)

2 麦克斯韦-玻尔兹曼分布计算统计平均值的困难

上述理论基于麦克斯韦-玻尔兹曼分布给出了计算宏观观测量即统计平均值的方法.但对一个实际的物理系统而言，其微观结构是非常复杂的，为了进行理论研究，人们通常通过建立模型来简化真实的系统.即便如此，可能出现的微观状态数目也是非常多的，而且通常其中很大一部分的微观状态出现的概率非常小.如果通过以上公式进行直接计算，其效率会非常低，即使使用超级计算机也需要消耗大量的时间.我们不妨从一个磁性材料来看，由于电子的自旋指向只有两种，自旋向上和自旋向下，我们可以建立一个简单的晶格模型——易辛模型来进行研究，该模型认为每个晶格格点会被一个电子占据，每个电子的状态可能会是自旋向上和向下，在数学上可以用+1和-1来表示.我们可以想象该模型是极度简化后的系统，实际物理系统要远比该模型描述的系统复杂.尽管如此，我们也会发现该模型很难进行直接计算：假设系统有N个电子，每个电子的状态(即自旋)用Si来表示，则Si可以取值+1或-1.那么，系统可能出现的微观状态数为2N个.对于一个真实的物理系统，N通常是一个很大的值(通常是和阿伏加德罗常数6×1023一个量级)，对应的状态数2N则是一个天文数字.也就是说，系统的状态数随系统的自由度是一个指数增长的关系，人们无法在任何计算机上演化所有这些可能的状态，更无法精确地数值计算系统的统计平均值[8].

3 按概率分布近似求解易辛模型

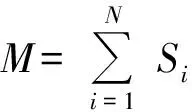
(4)

如果我们定义平均每个自旋的磁化率

(5)

上述情况我们考虑了自由电子的情况，但在实际物质中，电子间是存在相互作用的，为了简化问题，我们只考虑相邻近的自旋间存在相互作用的情形.此时系统的能量可以用下式来表达，也就是易辛模型的哈密顿量

(6)

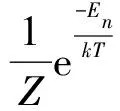
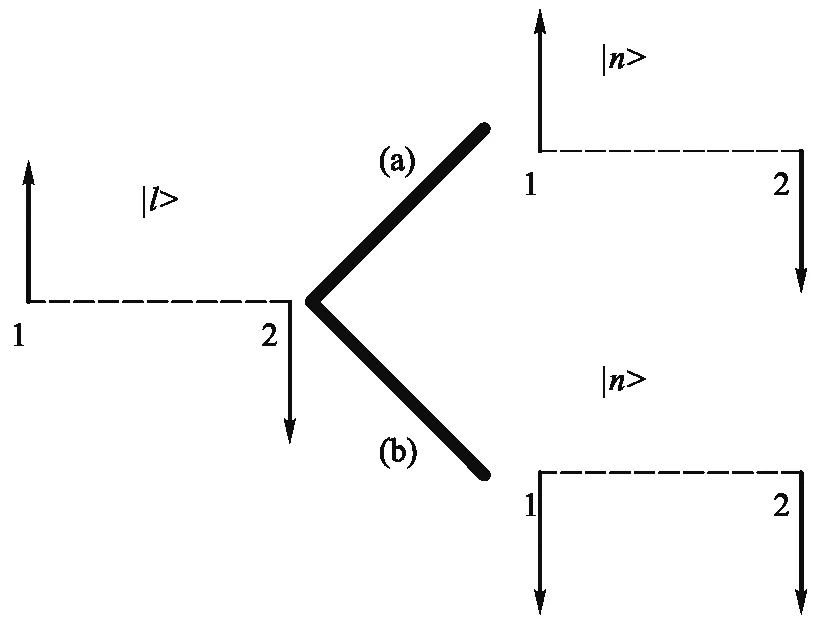
图1 以两个电子的自旋指向为例，演示系统状态的演化过程：初始时刻两个格点上电子自旋分别为向上和向下.(a) 尝试翻转自旋1但该翻转被拒绝，则系统的新状态|n>和之前的状态|l>一致；(b) 尝试翻转自旋1并接受该反转，系统状态由|l>转变为|n>，即两个自旋均向下

通过上面的状态演化过程，我们可以发现，对任意一个初始的系统状态，它向更高概率状态演化的可能性要大于向更低概率状态演化的可能性.也就是说，即使初始状态的玻尔兹曼概率非常小，它也会逐渐向高概率状态进行演化，并且不会再回到小概率的状态，而是在一些高概率的状态间进行演化.而且我们知道这些高概率状态的数目是非常少的，从而能够用计算机实现这些状态间的演化，计算这些高概率状态的玻尔兹曼概率并计算统计平均值.在有限长的演化过程中，可以近似得到系统宏观统计平均值的近似值：

(7)

其中Mm是观测的次数.对比式(2)可以发现，这里计算A的统计平均值只是一个简单的平均，没有进行加权.这是因为每个状态出现的权重已经在微观状态的演化过程中体现出来了.这种方法可以在无穷多的可能微观状态中找到概率较大的微观态，而忽略概率很小的微观态(这样的态往往占绝大多数)，从而使得求统计平均值变得简单.当然这种方法忽略了小概率的状态，会带来一定的统计误差.但根据大数法则和中心极限定理，当观测次数Mm较大时，该近似的效果和精确值达到一致，统计误差可以忽略.

4 在易辛模型中的计算结果

使用这种方法，我们计算了二维正方晶格中易辛模型的平均每自旋的基态能量和平均每自旋的磁化率随温度的变化关系，分别如图2和图3所示.在该计算中，我们选取相互作用强度J=1，即系统具有铁磁性，并且设置玻尔兹曼常数k=1.
图2和图3的横坐标都是温度T，我们选取离散的T的值进行计算，T的选取范围从0到3，步长选取为0.02，由于该步长选取的足够小，所以图2和图3中给出的不是离散的点，而是连续的曲线.由于该计算是在有限大小的晶格上进行的，不同大小的晶格上的计算结果会有所不同，即会出现有限尺度效应.通常情况下，晶格越小，有限尺度效应越明显，而当晶格足够大的时候，有限尺度效应可忽略，即所得计算结果接近于热力学极限下的值.对所有的T的值，我们首先选取正方晶格大小为100×100，即N=10000个格点.那么对每一组参数设置(如N=10000，T=0.1，J=1和k=1)，我们可以从任意一个系统状态(即10000个格点上自旋的任意分布)出发，通过玻尔兹曼概率来进行系统新旧状态的演化，最终使得系统达到平衡态，然后在系统动态平衡下进行大量的测量并求统计平均值，即可得到感兴趣的物理量如能量E和每自旋的磁化率m等.对部分的T的值，我们还进行了N=120×120的计算得到的结果与N=100×100的结果几乎没有差别，说明所选的系统尺寸已经足够大，有限尺度效应可忽略.

图2 二维易辛模型中 每自旋的能量随 温度的变化曲线

图3 二维易辛模型中 每自旋的磁化率m 随温度的变化曲线

从图3中我们可以看到，m随T的变化曲线有两条，即随着T的降低，一条趋向于m=1，一条趋向于m=-1.在具体的计算中，m出现正值或者负值与初始状态的选择有关.这二者是完全等价的，前者对应着最终所有的自旋都是向上的，后者对应着最终所有的自旋都是向下的，它们都表示系统最终趋于铁磁态，而且温度越低，铁磁性越明显.该结果说明系统的铁磁性随温度的降低越来越强，并且有一个转变的温度Tc≈2.27，当温度高于该转变温度时，系统铁磁性完全消失.

5 结论

综上所述，我们讨论了麦克斯韦-玻尔兹曼方法在统计物理中的应用，并以易辛模型为例进行了求解，研究了易辛模型中出现不同微观态的概率，进而计算了该模型的基态能量和磁化率.我们首先考虑系统所有的粒子间无相互作用的情况，此时系统所有微观状态都具有相同的能量，微观态的数目是随着平均每个自旋的磁化率m的增大迅速减少的，说明系统最可能出现的状态是对应着m=0的.由此可见，在系统所有可能的2N个微观状态中，大多数状态对应的概率很小甚至可以忽略不记，所以可以只考虑少数玻尔兹曼概率较大的状态即可.当考虑粒子间相互作用时，由不同微观状态的玻尔兹曼概率之比可以进行系统微观状态间的演化，只抽样出现概率大的微观态而忽略概率很小的微观态，从而得到宏观观测量的近似值，并且该近似值随着观测的次数增加而趋于精确值.这说明麦克斯韦-玻尔兹曼方法并不仅仅告诉我们系统某个微观状态的玻尔兹曼概率，而且可以极大的简化统计观测量的求解.该思想并不局限于求解本文中举例的易辛模型，我们可以将该方法推广到更复杂的模型来求解更多复杂的宏观观测量如压缩率和结构因子等，说明麦克斯韦-玻尔兹曼方法在统计物理模型中具有广阔的研究前景.