双层转角石墨烯结构的构建方法浅析
2021-08-19陈明星
陈明星
(湖南师范大学 物理与电子科学学院,湖南 长沙 410081)
2004年,英国曼切斯特大学A. Geim教授小组从石墨中剥离出碳的单层结构——石墨烯,从此掀起了二维材料的研究热潮[1]. 石墨烯也因此在过去的十多年中一直是凝聚态物理领域的研究热点. 由于石墨烯的层状结构,且层间相互作用很弱,因此人们可以通过不同的堆叠方式设计具有新奇物理性质的新结构. 比如,双层石墨烯中两者相对旋转一个较小的角度时可形成莫尔条纹,该转角结构产生的摩尔周期势将石墨烯原胞的能带折叠到一个很小的超胞布里渊区中,并且导致两层石墨烯中的狄拉克电子态杂化,从而对其电子的费米速度等一系列性质产生重要影响[2-7]. 当转角在大约1.1°时,转角石墨烯形成的莫尔周期势作用导致平带的出现[8]. 该角度的双层石墨烯被称之为魔角石墨烯. 2018年,美国麻省工学院Pablo Jarillo-Herrero研究组在魔角石墨烯中实现莫特绝缘体和超导电性[9,10],再次将石墨烯的研究推向高潮.
将凝聚态物理前沿科研成果引入固体物理和固体电子结构相关的课程教学,既能使学生了解前沿研究动态、培养学生的学习兴趣,又能增强学生运用书本知识解决实际问题的能力. 石墨烯由于其简单的晶体结构和特殊的能带结构,已经被同行作为固体物理等相关课程教学的经典例子[11-14].
晶体结构决定其性质,了解晶体结构是进一步研究晶体电子结构和物理性质的前提,因此固体物理教学大纲要求学生掌握描述晶体结构的数学方法.本文结合笔者自身的教学经历,以转角石墨烯为例,向学生展示如何构造双层转角石墨烯的结构,增进学生对描述晶体结构的数学方法和晶体具有周期性这一特性的理解.
1 石墨烯的晶体结构
石墨烯具有六角蜂窝状结构(见图1).假设其晶格常数为a,则原胞基矢为
(1a)
(1b)

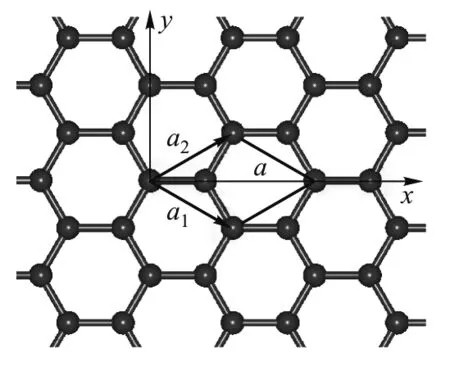
图1 石墨烯的结构. a为晶格常数,平行四边形代表原胞,黑色箭头代表原胞的两个基矢a1和a2.
2 石墨烯超胞的构建
2.1 变换矩阵
石墨烯超胞基矢Ai与原胞基矢ai的变换关系为
(2)
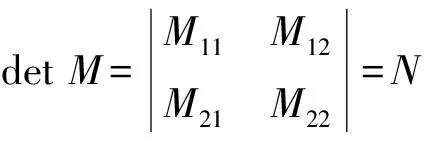
(3)
2.2 超胞结构的构造
假设原胞中第α个原子的坐标为Pα=xαa1+yαa2, 即Pα用分数坐标(xα,yα)表示,并且满足0≤xα,yα<1,则晶体中该原子通过平移一个正格子格矢得到的原子位置坐标Pn为
Pn=(n1+xα)a1+(n2+yα)a2
(4)
ni为整数.Pn也可用超胞的基矢表示为
Pn=XαA1+YαA2
(5)
由此,可以得到
(6)
将式(3)代入式(6)可得
(n1+xα,n2+yα)M-1=(Xα,Yα)
(7)
上式给出了如何计算Pn用超胞基矢表示的分数坐标(Xα,Yα).Xα、Yα的取值可以是任意数值.若Pn位于坐标轴原点的超胞中,则0≤Xα,Yα<1.

图2 石墨烯超胞结构.其晶格常数为黑色和浅色平行四边形分别原胞和超胞. 黑色和浅色箭头代表分别代表原胞和超胞的基矢. 超胞基矢用A1、A2表示.

表1 石墨烯超胞结构中各原子的坐标.

X′α=Xα-Nx
(8a)
Y′α=Yα-Ny
(8b)
Nx、Ny为可正可负的整数.上述过程还需排除重复得到的原子.上述超胞的构建也可以借助当前的晶体结构可视化软件VESTA完成. 具体操作流程:打开VESTA操作界面并输入相应的原胞结构,之后点击Edit—Edit Data—Unit Cell—Transform matrix. 在Rotation matrix填入上述变换矩阵的转置即可.
3 双层转角石墨烯的构建
转角石墨烯由两个大小相等的石墨烯超胞堆叠而成,其层间距强烈依赖于局部的原子堆垛方式,平均层间距大约在3.5 Å左右. 两层石墨烯的相对转角越小,超胞越大. 为保证上下两层有转角,其超胞变换矩阵需不同.

图3 转角石墨烯的构造. 黑色和浅色平行四边形代表两石墨烯超胞,其基矢分别用Ai和A′i表示,θ为两超胞的相对转角,浅色虚线沿Ri=ia1+ia2.

(9a)
(9b)

表2 部分小转角双层石墨烯中超胞与原胞之间的变换矩阵.
采用分数坐标的好处之一是旋转超胞基矢时,若原子分数坐标保持不变,则晶体结构做相应的转动.从图3可以看出,同一原子在不同的超胞中分数坐标不同.如果使上层石墨烯超胞的基矢与下层石墨烯超胞保持一致,且原子的分数坐标(Xα,Yα)保持不变,则上层石墨烯相对下层石墨烯有θ角度的旋转.进一步将所有原子坐标放入一个文件,并做成晶体结构可视化软件(比如VESTA)可识别的文件格式,可得到双层转角石墨烯的结构图.
图4给出了2.13°转角双层石墨烯的结构俯视图.

图4 2.13°转角双层石墨烯的结构.两层原子分别用不同的颜色表示并给出了AA和AB堆叠的局部原子结构,黑色平行四边形代表一个超胞.
4 小结
本文介绍了石墨烯的晶体结构,阐述了结合晶体周期性和超胞-原胞之间的变换矩阵构造超胞结构的方法,并将其运用到双层转角石墨烯结构的构造,可作为固体物理课程教学的一个例子,有利于学生掌握描述晶体结构的数学方法.
