2020年山东卷21(2)之我解及文(1)纠正
2021-08-19许银伙
许银伙
(福建省泉州外国语中学 362000)
原题再现已知函数f(x)=aex-1-lnx+lna.
(1)当a=e时,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积;
(2)若f(x)≥1,求a的取值范围.

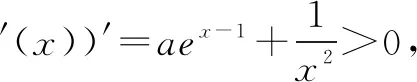
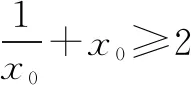
我解方法二(特值代入法)由f(1)=a-lna≥1得a≥1,所以a<1不符合要求.
(1)当a=1时,f(x)=ex-1-lnx,要证f(x)≥1,即证ex-1≥1+lnx.易证:
ex-1≥x(当且仅当x=1时取等号)且lnx≤x-1(当且仅当x=1时取等号),所以ex-1≥1+lnx成立.
(2)当a>1时,f(x)=aex-1-lnx+lna>ex-1-lnx,由(1)得f(x)>1恒成立.
综上得:所求a的取值范围是[1,+∞).
评注函数f(x)中含有ex-1和lnx很自然会想到取x=1代入尝试,以缩小关于参数分类讨论的范围.当a=1时,本解法中利用两个常见不等式结论解决;当a>1时,运用放缩法利用当a=1时的结论.本解答参考了文[3]和文[4]的技巧,也参考文[1]和2013年全国高考理科(Ⅱ)卷21题的解答.

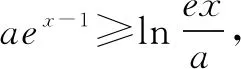
综上得:所求a的取值范围是[1,+∞).
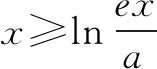

3.函数y=ex过原点的切线是y=ex,结合图形或者通过导数可以得出不等式ex≥ex恒成立,是解决函数导数问题的常用结论.

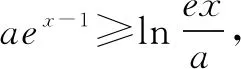

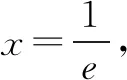
评注虽然上面的两种方法都是通过构造新函数解决,但因为构造的函数g(x)=xlnx并不是在原来函数f(x)定义域上的单调函数,因此必须分段讨论.构造的函数选择能在定义域内单调,通常是减少思维量和运算量的诀窍.
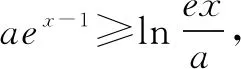
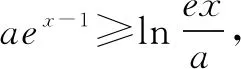

通过对文[1]的学习,可以大大加深对同构函数解决问题的印象和技巧的掌握,针对文[1]给出高考压轴题的同构函数的两类常见形式,笔者给出更宽泛的概括:凡是见到式子中同时含有三个变量x,ex,lnx,都可以考虑把式子变形成其中一侧含x,ex类型,另一侧含elnx,lnx类型,然后构造函数,且争取让构造的函数具有单调性.
