例谈表格模型在高中化学计算中的应用
2021-08-19迟宇前
迟宇前
(云南师范大学附属中学呈贡校区 650500)
一、建立表格模型
若有AaBb和CcDd两种物质(A、B、C、D为原子种类,a、b、c、d为原子个数),其中A、B、C、D原子的相对原子质量分别为为MA、MB、MC、MD.即可求出两种物质中A、D原子个数比为a∶d;A、D元素质量比为aMA∶dMD;具体过程见表1.

表1 建立表格模型
本文中m代表质量,Mr代表相对分子质量,M代表摩尔质量,n为物质的量,N为微粒个数,NA为阿伏加德罗常量约为6.02×1023,V为体积,Vm为气体摩尔体积,标况下气体的摩尔体积约为22.4L·mol-1,p为压强,T为温度,ρ为密度,c为摩尔浓度.
二、表格模型的应用
1.利用n、N、NA、m、M、V、Vm之间的关系,求比值
高中化学教学中,利用n=m/M;n=N/NA;n=V/Vm之间的计算是高中化学计算中的重点和难点,由于公式间转化错综复杂,学生计算过程中综合性比较强,利用表格模型,可以帮助学生轻松、快速的理清思路,解决问题.
例1质量比为3∶2的O2和O3,下列说法正确的是( ).
A.分子数之比3∶2
B.原子数之比1∶1
C.同温同压下气体的体积之比9∶4
D.物质的量之比4∶9
分析A中n=m/M,即物质的量之比为9∶4,因为分子个数与物质的量成正比,故分子个数比为9∶4,故A错误;B中一个O2分子中有2个氧原子,一个O3分子中有3个氧原子,故氧原子个数比为9×2∶4×3=3∶2,B错误;C中同温同压下气体的体积与物质的量成正比,故体积比为9∶4,故C正确;D错误.故选C.建立表格模型,具体过程见表2.
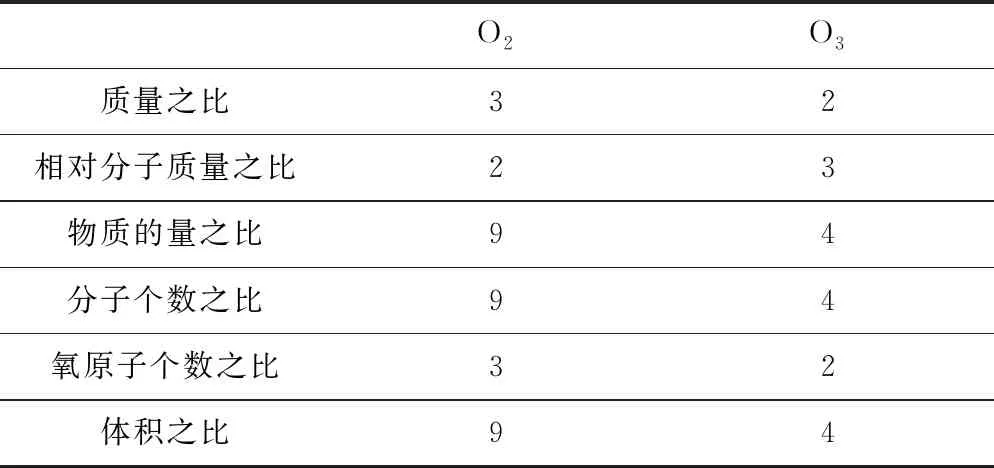
表2 利用n、N、NA、m、M、V、Vm之间的关系,求比值
2.与阿伏加德罗定律及其推论有关的求比值问题
阿伏加德罗定律说的是同温同压气体的体积与物质的量成正比.结合玻意耳定律和盖·吕萨克定律可得出理想气体状态方程pV=nRT(R=8.314J·mol-1·K-1).利用理想气体状态方程决阿伏加德罗定律及其推论的相关计算是高中化学学习的重点.
(1)利用pV=nRT,求比值.
例2标准状况下,关于22.4 L CO和17 g NH3的说法错误的是( ).
A.物质的量之比21
B.原子数之比1∶2
C.体积之比1∶1
D.分子数之比1∶1
分析A中,标况下22.4 L CO气体的n=22.4L/22.4L·mol-1=1 mol;17g NH3的n=17g/17g·mol-1=1mol,物质的量之比等于1∶1,故A错误;B中一个CO分子中有2个原子,一个NH3分子中有4个原子,故原子个数比为1×2∶1×4=1∶2,B正确;C同温同压下气体的体积与物质的量成正比,故体积比为1∶1,故C正确;D中分子个数与物质的量成正比,分子个数比为1∶1,D正确.故选A.建立表格模型,具体过程见表3.
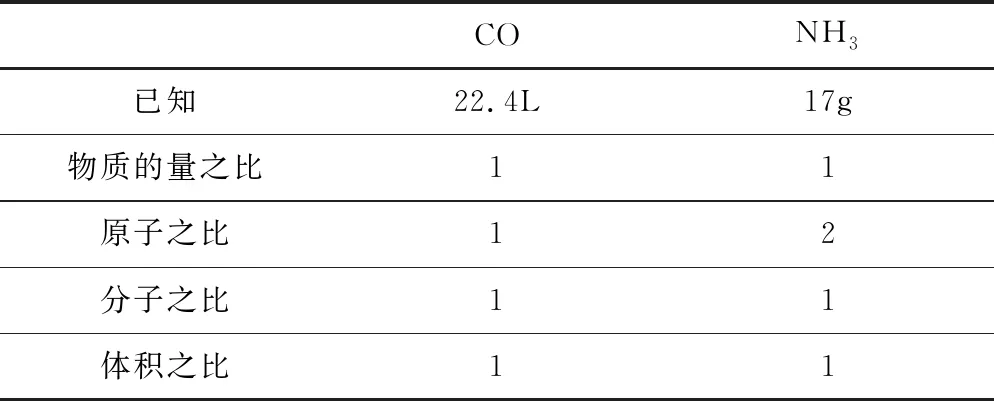
表3 利用pV=nRT,求比值
(2)利用pM=ρRT,求比值.
例3在标准状况下空气的平均式量为29,相同条件下下列四种气体中密度比空气大的有____.
①H2②CO2③HCl ④Cl2

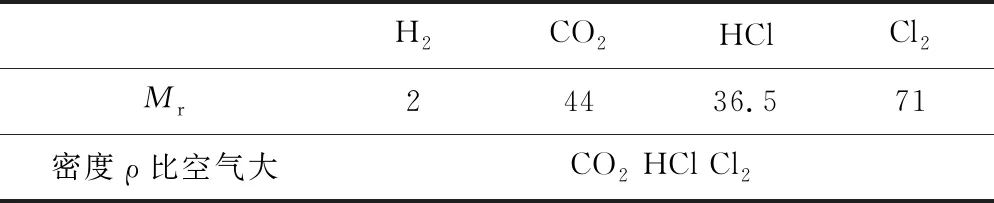
表4 利用pM=ρRT,求比值
3.利用c、n、V之间的关系,求比值
例4等体积的Na2SO4、KAl(SO4)2、Al2(SO4)33种溶液分别与等体积、浓度的BaCl2溶液完全反应,则3种溶液的摩尔浓度之比为:____.
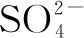
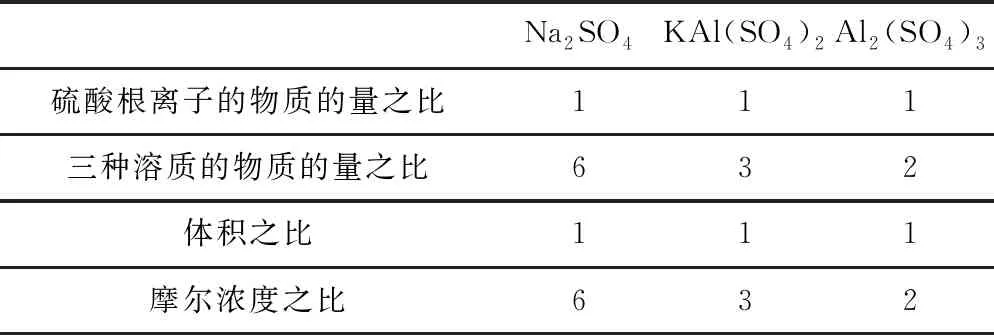
表5 利用c、n、V之间的关系,求比值
通过构建思维模型,把相关的问题合并为一类问题,实现“多题一解”.此方法还可用于化学反应速率,平衡移动,电化学等问题,同时也为其他复杂计算中寻找“多题一解”,提供了思路.
