对一类椭圆定值问题的探究

蒋 振

(广东省惠州仲恺中学 516229)

一、问题引入

题目(2020年南昌市NCS20200607项目第一次模拟考试理科第20题)己知圆F1：(x+1)2+y2=r2(1≤r≤3)，圆F2：(x-1)2+y2=(4-r)2.

(1)证明圆F1与圆F2有公共点，并求公共点的轨迹E的方程；

(2)已知点Q(m,0)(m<0)，过点F2斜率为k(k≠0)的直线与(1)中轨迹E相交于M,N两点，记直线QM的斜率为k1，直线QN的斜率为k2，是否存在实数m使得k(k1+k2)为定值？若存在，求出m的值，若不存在，说明理由.

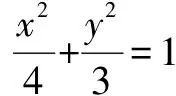
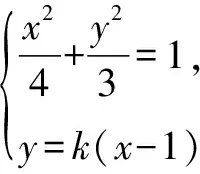
(4k2+3)x2-8k2x+4k2-12=0.

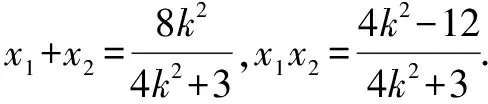
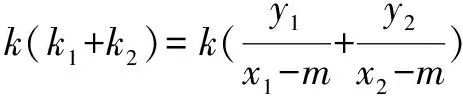
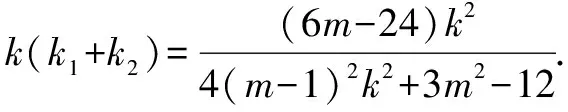
因为m<0，所以当3m2-12=0时，即m=-2时，k(k1+k2)=-1.

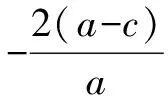
二、问题探究

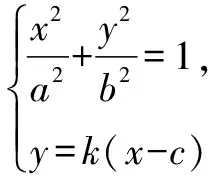
(a2k2+b2)x2-2a2k2cx+a2k2c2-a2b2=0.

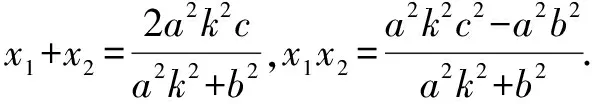
①

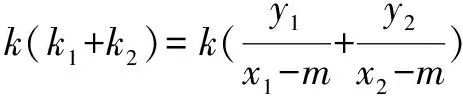
三、问题推广