高中生数学解题中错误原因分析与教学策略探析

徐 丽

(安徽省广德市第三中学 242200)

素质教育改革要求对学生的教学要以培养学生的学习能力、开发学生的思维为中心，特别是在高中数学课堂上，要重视对学生的解题能力的锻炼，促进他们思维和创造力的培养.而在解题中，教学效果不够理想，当前的教学模式比较单一和固定，在方式和手段上不够科学，也不具有针对性，没有对学生出现的错误类型和原因进行深入分析，导致很多学生在同一个问题上出现了多次问题，特别是一些基础概念性问题成为了部分学生常常出现的错误，导致解题能力一直无法提升.因此教师要引导学生学会分析自己在解题过程中出现的问题，有针对性地培养解题思维.

一、高中生数学解题中出现的错误原因

1.运算能力差，出现计算失误

高中数学学习中，对学生的思维能力要求较高，很多题目都需要实现思维的转换，利用新旧知识的结合，将函数、几何甚至是代数的知识融合起来，才能解决问题，这也就导致很多学生在解题的过程中，过于关注解题思路的发展和研究，长此以往，自己的计算能力也出现了问题，导致很多基本的计算概念知识逐渐遗忘，在实际解题的过程中，就容易出现各种计算错误.而很多高中数学题的解题过程是环环相扣的，如果出现了一次错误，会影响后续的运算过程全部出现问题，这就导致学生在解题的最后就会面临无解以及解答错误的结果.而一旦出现了问题，学生可能由于思维定势的原因会忽视计算问题，过多地关注自己的解题思路，对学生自信心的打击比较大.

2.审题不清，忽视隐含条件

审题问题是很多高中生普遍存在的错误原因，而不同于小学和初中数学解题过程中出现的看错条件、单位或者数字等低级错误，高中生犯得最多的错误是对题目的条件和结论等信息缺乏整理、推论和分析的能力，这就导致他们无法找到有用的条件，对于题目不同的形式以及内容背后隐藏的条件不理解，学生就无法找到快速有效的解题方案，导致解题过程比较复杂，思路繁琐，学生的解题信心也会受到打击.所以很多高中生没有掌握审题的技巧，不能根据题目的条件进行深入分析和推导，给解题带来更多的困难.

3.概念原理掌握不牢靠，运用时容易混淆

虽然高中数学题一般包含了不同类型的知识内容，解题思路也比较复杂，对学生思维能力和变通能力的要求比较高，但是归根结底还是需要从基本的数学概念上进行延伸，了解数学理论的本质和内涵，才能达到熟练应用的效果.但是很多高中生在学习时眼高手低，忽视了对基本概念性质的学习和掌握，针对某些概念的运用方式和使用的范围还模糊不清，不能够分清不同概念之间的联系和区别，运用时就会出现各种错误.而一旦基础知识出现问题，解题时必然会困难重重.在选择解题策略时，也会因为对概念不熟悉而无法选择科学的方式进行解题.例如,已知函数y=1/2cos2x+√3/2sinxcosx+1,该函数的图像可由y=sinx图像经过怎样的平移和伸缩变换得到.而很多学生在解题是对周期变换和相位变换的概念混淆，得出的答案自然也会偏离方向.

二、高中生数学解题教学的有效策略

1.加强概念性知识教学，提升基本运算能力

在高中数学解题学习中，基本的概念性知识是解题的钥匙，也是学生必须掌握的，很多基本的定理在运用中可以发挥重要的作用.所以教师在新课教学中应该以培养学生扎实的基本功为目的，从不同的角度引导学生理解概念和性质，比如,集合的分类和性质，函数的定义，变量、自变量、因变量之间的关系，而这些基本的知识在后面各种函数知识的学习中发挥着重要的作用，是学生在解题中必须要引用和牢记的性质.其次计算仍然是基本功，而很多高中生会忽视基础的计算训练，基本的运算技巧掌握不牢靠.教师要对学生进行有目的地训练，在平常的课堂教学中，有意识地引导学生进行计算训练，可以从基本的概念着手，实现概念和计算同步教学，引导学生从概念入手训练运算能力，提升学生的综合实力.

2.重视理论和实际结合，提升分析能力

教师在教学中要引导学生去把握解题的思路，引导学生将理论和实际问题结合起来，理清自己的思维，有条不紊地对题目进行深入分析，从而找到正确的解题方向，逐步推演出解题的思路.其中，学生必须在审题之后，去分析出题的意图和考察的知识点，根据自身的经验，结合所学的知识，将可能应用到的理论都理出来，再通过深入探索，找到一些解题的路径，不断尝试和排除，迅速找到最简便快捷的解题方法.

例1 若不等式2x-1>m(x2-1)对于所有的-2≤m≤2都成立 ，则x的取值范围是多少？

本题可以把m视为主变元，将原不等式化为m(x2-1)-(2x-1)<0,令f(m)=m(x2-1)-(2x-1)，再由题意得到f(-2)<0,f(2)<0,当-2≤m≤2时，f(m)<0恒成立，只需要满足-2(x2-1)-2(2x-1)<0,2(x2-1)-2(2x-1)<0,即可解得x的取值范围.

在上述例题中，分离参数时，会出现分离出参数与变量，所以需要进行思维角度的变换，实现“反客为主”，将习惯上的主元变与参数变量的地位进行变换，变个视角来重新审查恒成立的问题，从而可以实现对题目的降次和化简的目的.因此在教学中，教师要根据实际问题和条件来进行解题，帮助学生实现思维的变换，才能掌握巧妙的解题技巧.

3.实施科学训练，培养学生的数学思维

在解题过程中，学生的思维转换能力尤为重要，学生不仅要掌握基本的解题方法，还要不断提升自身的创造力，才能培养举一反三的能力，在面对千变万化的题目时，能够挖掘题目中的有效信息，找到更多创新的解题思路，从而提升解题能力.首先，教师要对学生进行科学训练，以质量为前提，摒弃传统模式，让学生能够有更多的空间和时间去思考和反思.教师可以让学生准备错题集，定期对自己的错题进行整理，发现自己易错的知识点，才能更加准确地进行反思和巩固，弥补自己的错误，不断优化自身的知识体系，提高解题的质量.

例2已知a,b为正实数，2b+ab+a=30,求函数y=1/ab的最小值.

该题是一个二元函数的最值问题，教师可以先引导学生思考可以通过什么途径进行解答，比如可以使用消元，转化为一元函数问题；或者只用基本不等式的公式，考虑放缩后，通过解不等式的方式来解答.然后教师可以让学生深入思考需要用到什么相关的公式，帮助学生理清思路，才能更好地提高解题能力.

4.巧用画图技巧，掌握科学解题方法

在高中数学解题中，画图作为一种重要的辅助方式，对提升学生的解题能力具有重要意义，而学生在解题中出现的思路不清晰、分析不到位等情况，都可以通过画图来实现对题目的分解，从而对具体的题目进行灵活变形.比如f(x)≥g(x)，就能够非常容易画出不等号两边函数的图像，可以直接通过画图来得出结果，因此在选择题和填空题的解题上，会更加方便和快捷.

例3求证：f(x)=(x+1-a)/(a-x),对于x∈[a+1,a+2]，该函数单调且恒有-2≤f(x)≤-3/2成立.

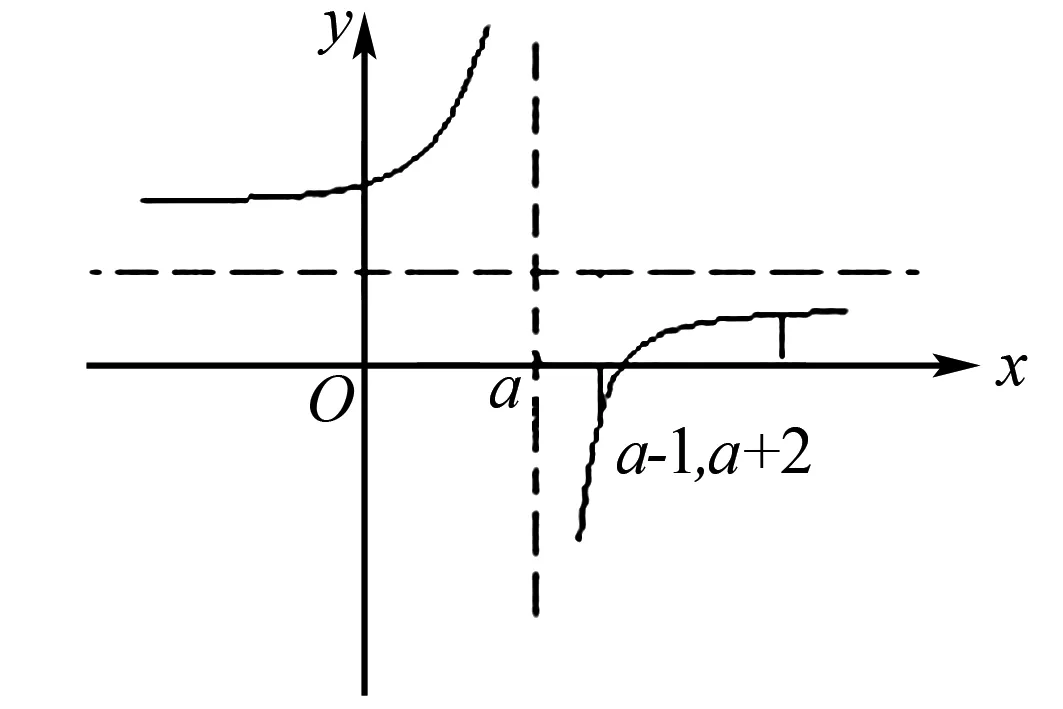
解析原方程可以化为y=1-1/(x-a),由图像可知，x∈[a+1,a+2],该函数单调递增，f(x)≤f(a+2)=1.5,f(x)≥f(a+1)=-2,所以可以得证.

综上所述，在高中数学课堂上，学生在解题中容易出现各种错误，面对学生出现的各种问题以及教学中的各种阻碍因素，教师应该保持耐心，深入分析原因，找到问题所在，再结合不同学生的问题来优化教学和指导方式，根据不等式知识的特点科学教学，重视对学生审题意识、创造能力以及思维方式的培养，帮助其掌握正确的解题思路，提高学生整体的解题能力.