晶体双折射理论的回旋分解波法
——以单轴晶体为例
2021-08-19何健
何 健
(绵阳师范学院数理学院,四川绵阳 621006)
0 引言

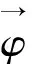
1 晶体双折射理论的波动方程
1.1 介质中的麦克斯韦方程组
光波是一种电磁波,晶体中光的传播可用麦克斯韦方程组和晶体的光学性质来分析[6].在均匀、不导电、非磁性的各向异性介质中,如果没有自由电荷的存在,麦克斯韦方程组为:
(1)
在描述介质中的电磁场,除麦克斯韦方程组的积分形式外,还需要物质方程:

(2)
1.2 介电张量下的非典型波动方程
对(1)第二式两边取旋度,考虑其第一式及(2)二式,可得[8]:

(3)
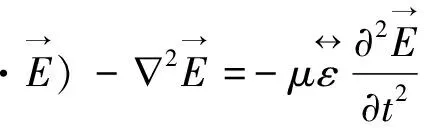
(4)
(5)

2 回旋波分解法
2.1波动函数的分解及约束条件

(6)
伴随约束条件:
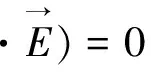
(7)
(8)

(9)
可见,此部分描述的是具有典型波动行为的解:
所以由上式,考虑非磁性介质特性(μ=μ0)可得:
(10)
可解得:
(11)
其中:
(12)
故:
(13)

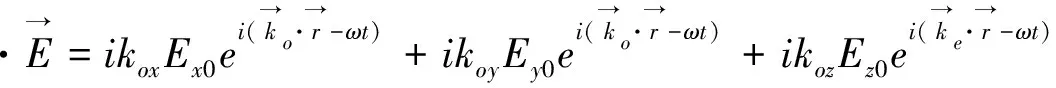
(14)
故:
(15)

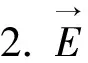
(16)
此时不构成行波,故不能传播能量.
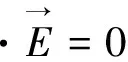
则需kez=0,kox=0,koy=0,得:
(17)
此时的光波由x、y方向的电振动形成的波数为ko且沿z方向传播的波与由z方向振动形成的波数为ke且沿垂直于z轴方向传播的波动的合成,其合成波矢(及折射率)将与方向有关,此即为e光.因此其合成波数取值介于z向的为ko及垂直于z向(或表为r向)的ke之间,自然表达为:
(18)
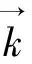
(19)
及折射率关系:
(20)
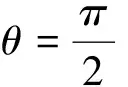
2.3 解的回旋波部分
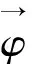
代入(4)式有:
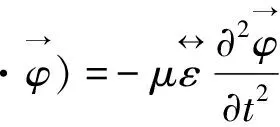
(21)
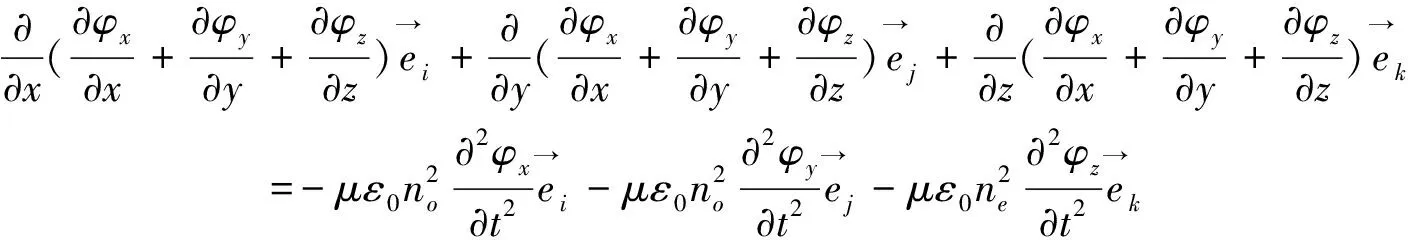
所以有:
(22)
由(22)式有:
(23)
(24)
代入(23),可得:
(25)
故:
(26)
进而得出:
(27)
将(27)代入(22)第一式,可得:
(28)
由此可得:
φx=φx0ei(kxx+kyy+kzz-ωt)
(29)

在此背景下,为了提高糖尿病肾病患者的早期诊断效果,对尿液 α1-MG、β2-MG、TRF、mAlb和 Cys-C 进行联合检测。其中α1-MG由人体的肝脏和淋巴细胞合成的糖蛋白。正常情况下α1-MG存在于人体各种体液和淋巴细胞膜的表面,但当人体出现异常情况时,如肾小球的过滤能力不足、肾小管吸收α1-MG能力降低时,可导致α1-MG升高。因此α1-MG可用于糖尿病肾病患者肾小球早期损伤的判定指标之一。
(30)
而对于(30)式中的kx,ky以及kz.可以通过下面的运算,将其做出代换.首先将(29)代入(28),可得:
(31)
又(31)式两边同时乘ikx,可得:
(32)
又由于其满足限制条件:
所以有:
∇2φx=0
将(29)代入上式有:
即:
(33)
将(33)代入(32),可得
(34)
通过上式解得:
(35)

(36)
正晶体的情况则为:
(37)
又如图1所示,可得:
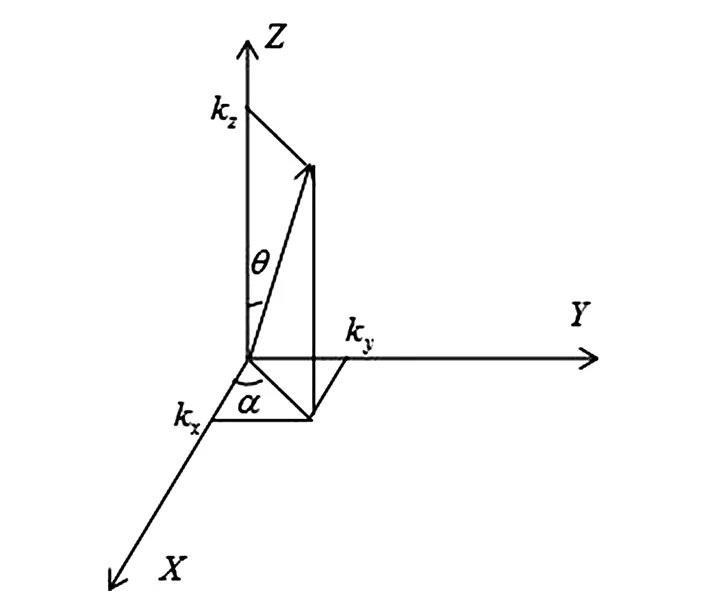
图1 回旋波波矢结构示意图Fig.1 Schematic diagram of cyclotron wave vector structure
(38)
又将公式(38)代入公式(33),可得:
(39)
由上式可得
(40)
(41)
将(38)代入(41),又可得
(42)
再将(38)、(40)、(41)、(42)四式代入公式(36-37),可得
(43)
上式即为我们所求的回旋波的波动解.
对于负晶体有no>ne,则
(44)

而对于正晶体而言有ne>no,则
(45)
(46)
2.4 关于波矢及折射率的分析
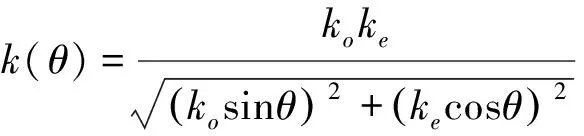
2.4.2 回旋波部分 对于回旋波部分的波矢及折射率的求解,我们可以由(34)式出发,可得
(47)
然后将(33)带入上式,可得
(48)

将上式代入(48)上式化为
(49)
又
(50)
将(50)式代入(49)式,可得
(51)
代入(51)式有
(52)
即为
(53)
又
(54)
代入(52)式有
(55)
进一步化简,可得
(56)
此时(56)化为
(57)
上式即为回旋波部分波矢的表达式,同时将(50)带入上式可得,回旋波波矢方向的折射率为:
(58)
3 小结

3.1 基础解与o/e光的成因分析
3.2 回旋波解与晶体椭球面形成的关系

3.3 后续工作
前面2.4的分析也意味着回旋波与基础解的波动拟合在折射率、波矢方面均相互吻合,两者的拟合只是造成波面沿不同取向的椭球曲率形态(并与晶体正负性质关联).当处理的问题涉及局域波动结构分析时,上述波动函数则提供了波动细节的诸多信息.而对于波矢与光线方向的关联、离散角等物理量几何量的表述则依赖于回旋波与基础解的拟合及几何分析,这也是本文的后续工作之一.
