关于H-矩阵Hadamard积的一个行列式不等式

刘俊同,李 龙

(1. 阜阳师范大学数学与统计学院,安徽阜阳 236041；2. 阜阳一中，安徽阜阳 236000)

0 引言

H-矩阵是一类特殊矩阵，它在计算数学、经济学、管理科学、神经网络和控制论等诸多学科都有着重要的应用.而矩阵的Hadamard积是一种特殊的矩阵乘积，它被广泛的应用于量子计算、编码理论、物理学和区组设计等问题中.基于这些重要的应用背景，H-矩阵的Hadamard积的特征值和行列式问题一直备受国内外专家学者的关注，关于这方面更多的内容请参见文献[1-9].

Oppenheim于1930年证明了下述不等式(见文献[1，P509])：给定两个n级半正定矩阵A和B，则有

(1)

其中A∘B表示矩阵A和B的Hadamard积，上述不等式称为Oppenheim行列式不等式.

Lynn[2]和Ando[3]分别推广了不等式(1)，它们差不多同时得到如下结果：给定两个n级半正定矩阵A和B，则有

等价地

(2)

Li 和Li在文献[4]中证明了如下结果：给定两个n级实的H-矩阵A和B，则有

(3)

其中Ak表示矩阵A的第k个顺序主子阵

Chen在文献[5]中推广了上述不等式(3)，得到了如下更整齐的结果：给定两个n级H-矩阵A和B，则有

(4)

其中μ(A)表示矩阵A的比较矩阵，具体定义见下一小节.

本文将利用数学归纳法、M-矩阵和H-矩阵的基本理论以及不等式的构造和放缩技巧推广不等式(4)到更一般形式.

1 符号、定义和引理

为了表述方便，首先介绍一些符号.设Cm×n(Rm×n)表示m×n复(实)矩阵的全体组成的集合，A≥0(A>0)表示矩阵A的所有元素都是非负(正)的 .对于两个相同级数的矩阵A和B，用A∘B表示矩阵A和B的Hadamard积，设A=(aij)∈Cn×n，常用Ak(k=1,2,…,n)表示矩阵A的第k个顺序主子矩阵，Aα表示矩阵A的指标位于α⊆{1,2,…,n}的主子矩阵.

定义1[10]称集合

Zn×n={A=(aij)∈Rn×n:aij≤0,i≠j,i,j∈{1,2,…,n}}

中的矩阵为Z-矩阵.

易知A=(aij)∈Rn×n是Z-矩阵的充分必要条件是存在α∈R，P∈Rn×n，且P≥0，使得A=αE-P.

定义2[10]设A=(aij)∈Cn×n，若A是Z-矩阵，且对任意的k=1,2,…,n，都有第k个顺序主子矩阵的行列式|Ak|>0，则称矩阵A是M-矩阵.

则称μ(A)为矩阵A的比较矩阵.

定义4[10]设A=(aij)∈Cn×n，若矩阵A的比较矩阵是M-矩阵，则称A是H-矩阵.

易证M-矩阵(H-矩阵)的每一个主子矩阵还是M-矩阵(H-矩阵).

为了陈述和证明主要结果，我们需要下述引理

引理1[3]设A=(aij)∈Rn×n是一个M-矩阵，若

特别地，有

(5)

引理2[2]若A和B是两个n级H-矩阵，且C=A∘B，则矩阵C也是一个n级H-矩阵.

引理3 设a和b是两个实数，且有a≥1，b≥1，则有ab≥a+b-1.

证明：因为a≥1，b≥1，于是有

ab-a-b+1=(a-1)(b-1)≥0

所以，有

ab≥a+b-1

2 主要结果

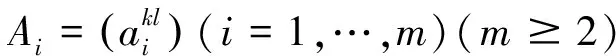
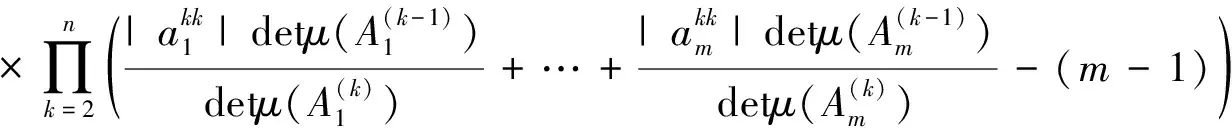
证明由引理2，知A1∘…∘Am仍是H-矩阵，对矩阵的个数k使用归纳证明.当k=2时，定理归结于Chen 的结果(4)，假设当k=m-1时，定理成立，即

成立，下证当k=m时，定理也成立，即证

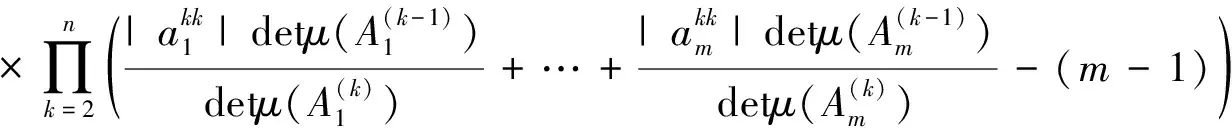
通过不等式(4)，有

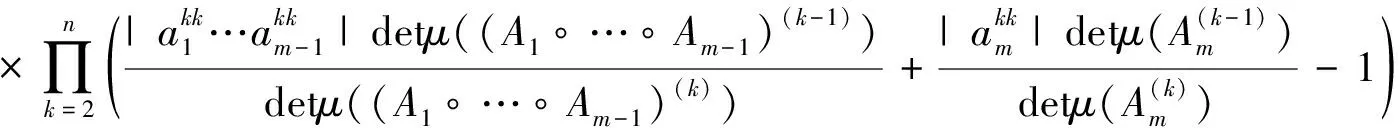
应用归纳假设，则有

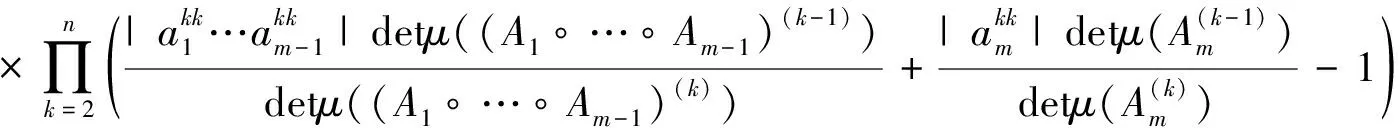
(6)

记

(7)

(8)

应用引理1，通过不等式(5)，有

(9)

因此有，

xk≥1,yk≥1

利用引理3，有

xkyk≥xk+yk-1

(10)

结合不等式(7)、(8)、(9)和(10)，不等式(6)进一步可化为

3 小结

本文结合H-矩阵的基本理论、矩阵Hadamard积的性质以及不等式的构造和放缩技巧，证明了H-矩阵Hadamard积行列式不等式的一个重要结果，推广了已有文献的结果.H-矩阵是一类应用范围极其广泛的矩阵，对H-矩阵理论展开研究一方面可以丰富H-矩阵理论，另一方面对矩阵理论也有一定的拓展意义.