基于工作空间的PUMA机器人臂长参数优化
2021-08-18胡旺宁
胡旺宁
(上海捷勃特机器人有限公司,上海,200030)
0 引言
机器人的工作空间是指机器人末端参考点(一般取手腕点)在关节角变化下所能达到的所有位置点的集合,是衡量机器人工作能力的一个重要的运动学指标[1]。在设计机器人本体时,这是首先需要考虑的问题。在选定了某一构型后,机器人的工作空间由臂杆长度和关节角范围决定[2]。机器人的工作空间有两个基本问题:一是已知机器人的臂杆长度和各个关节角范围,求取其工作空间,称为工作空间分析或工作空间正问题;二是已知机器人的工作空间要求,反过来求机器人的臂杆长度和各个关节角范围,称为工作空间综合或工作空间逆问题[1]。
工作空间正问题相比逆问题容易一些,但是从需求驱动的逻辑来说逆问题比正问题更具有实际意义。由于逆问题比较复杂,现有的很多研究方法往往是通过试凑法[3]或影响系数法[4]将逆问题转化为正问题求解。这种方法虽然可以将逆问题进行简化,但是只能得到次优可行解,无法做到结果优化。尽管可以在正问题中做到将工作空间体积最大化[5-6],然而也不等于逆问题求解的最优化,因为机器人的工作空间要求往往不是指整个工作空间,而是整个工作空间的一部分,通常为规则的几何形状。
本文以PUMA机器人为例,对其进行运动学分析,在此基础上通过数值法和图解法相结合的方法求解其工作空间,然后借助解析法建立基于工作空间的臂长参数优化模型(适当减小参数的个数),最后选择启发式的遗传优化算法对臂长参数进行优化求解,得到优化结果。
1 基于工作空间的PUMA机器人臂长优化建模
1.1 PUMA机器人运动学与工作空间分析
PUMA构型是一种典型的工业机器人构型,由6个旋转轴线垂直或平行的旋转关节串联而成[7]。如图1所示的弧焊机器人就是一款PUMA型机器人。

图1 弧焊机器人
按照John J. Craig的方法建立上述PUMA机器人的D-H连杆坐标系[7],如图2所示,其方法的特点是坐标系{i}固连于连杆i的首端关节副,其原点位于关节轴i上,坐标系的编号与关节轴的编号刚好一致。对应的D-H连杆参数表如表1所示。
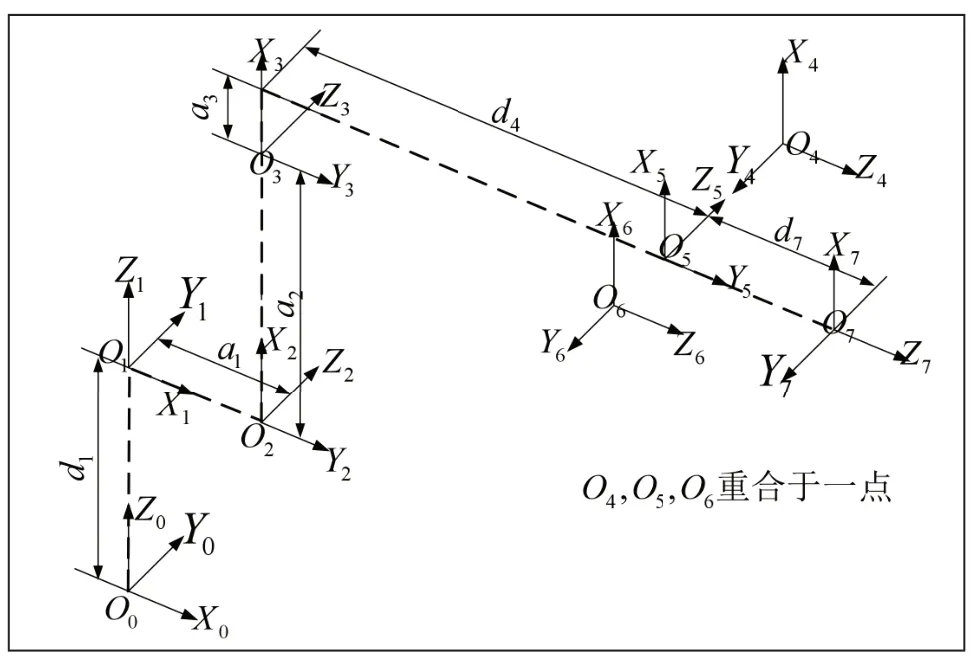
图2 PUMA机器人D-H连杆坐标系
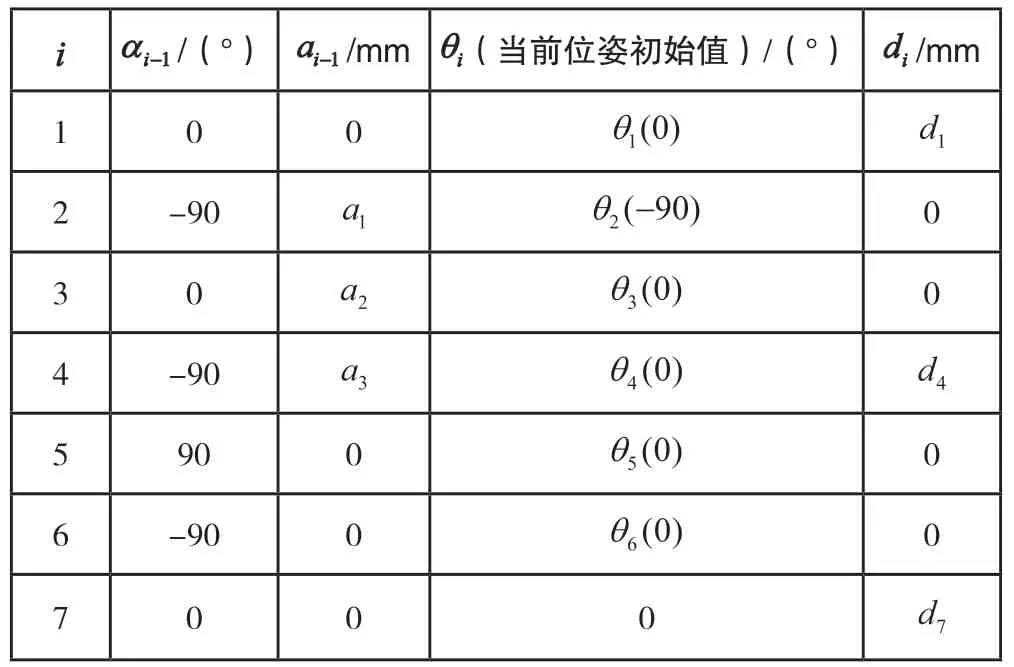
/(°)/mm (当前位姿初始值)/(°) /mm 1 0 0 2 -900 3 0 0 4 -90 5 90 0 0 6 -90 0 0 7 0 0 0

坐标系{3}相对于坐标系{0}的变换矩阵:


图3 PUMA机器人工作空间离散点分布图

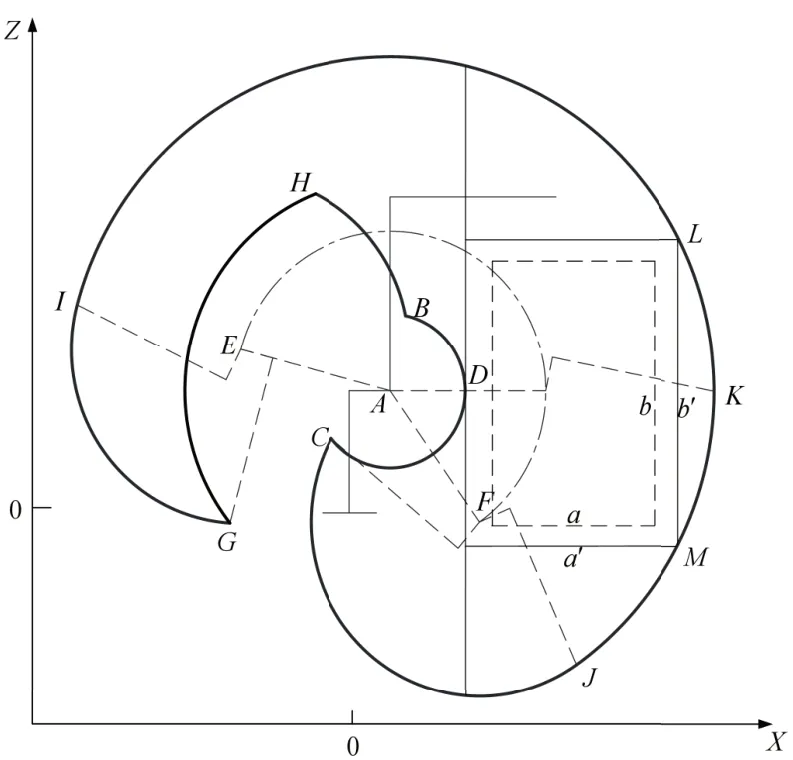
图4 PUMA机器人工作空间包络图
1.2 基于工作空间的臂长优化建模



1.3 基于工作空间的臂长参数优化模型
基于1.2节的分析,基于工作空间的 机器人臂长参数优化模型表述如下。

2 优化算法与实例分析
2.1 优化算法介绍
经典优化算法的原理是先建立目标函数与设计变量之间的梯度关系,然后沿初始值位置的负梯度方向进行搜索,当收敛差值小于设定的阈值即停止搜索,当前的设计变量值即为优化结果。经典优化算法的前提是目标函数与设计变量之间能够建立可以表达的映射关系。如果目标函数与设计变量之间是一种离散的、难以表达的复杂映射关系,那么就难以用经典优化算法来求解其优化问题。
启发式优化方法无需建立目标函数与设计变量之间可以表达的映射关系,是利用已有的经验,选择已经行之有效的解,以随机或近似随机方法搜索非线性复杂空间中的全局最优解。常见的启发式优化方法有模拟退火算法、遗传算法、蚁群算法、粒子群算法等。
遗传算法是一种模拟生物遗传选择和自然进化过程的搜索最优解的方法,其表达形式是针对一个群体中的所有个体,利用随机化的技术对一个被编码的参数空间进行高效搜索。其主要步骤有生成初始种群、编码、适应度评价、选择、交叉和变异,其中选择、交叉和变异构成遗传算法的遗传操作。
遗传算法的计算流程如图5所示:

图5 遗传算法计算流程
2.2 优化实例与结果分析


图6 初始变量下机器人工作空间


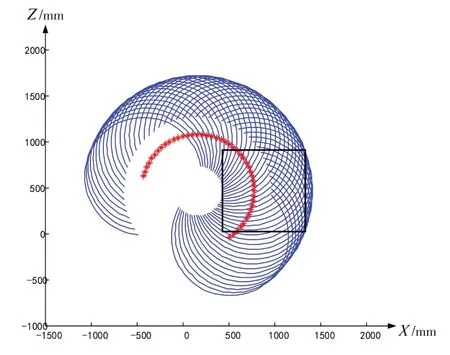
图7 优化变量下机器人工作空间

在初始设计变量条件下,目标函数值为1430,而在优化设计变量条件下,目标函数值为1351.5,优化率为5.5%。
3 结论
本文从实际需求出发,提出了一种基于工作空间的机器人臂长优化方法。首先建立机器人的运动学模型,基于运动学模型通过数值法和图解法相结合的方法求解机器人的工作空间,然后通过解析法建立基于工作空间的臂长参数优化模型,最后采用遗传算法对臂长参数进行优化求解。以PUMA机器人为例,给定工作空间要求,以臂长之和最小化为目标,采用上述优化方法,优化率达到5.5%。
