改进的Tietz-Hua势场Schrödinger方程的散射态解
2021-08-18陈文利冯晶晶
陈文利,冯晶晶,胡 艳
(西安培华学院 智能科学与信息工程学院,陕西 西安 710125)
引言
在非相对论、相对论量子力学的框架下,对于不同量子系统的精确解研究一直备受关注,但除氢原子、谐振子和Morse势等少数势场,大部分重要的势模型没有精确解,只能采用近似方法来处理并验证其有效性。此外,量子系统的精确解研究几乎都是针对束缚态而不是散射态的,不同于束缚态主要研究系统的离散能量本征值和本征态,散射态问题更多关注的是散射粒子的角分布以及散射过程中粒子性质的变化。近些年来,许多学者采用Pekeris类型的近似办法研究不同势场的薛定谔方程散射态问题,例如,Pöschl-Teller[1]、改良Rosen-Morse[2]和变形的Woods-Saxon[3]势等。Tietz-Hua势场是双原子分子振动能的最佳解析模型之一,在描述中、高转动量子数和振动量子数下的分子动力学时比Morse势场更有效[4-6]。在Tietz-Hua势场表达形式的基础上加上De(Ch-1/1-Che-bh(r-re))be-bh(r-re)项,就构建了一个改进的Tietz-Hua势场[7,8],其表达式为
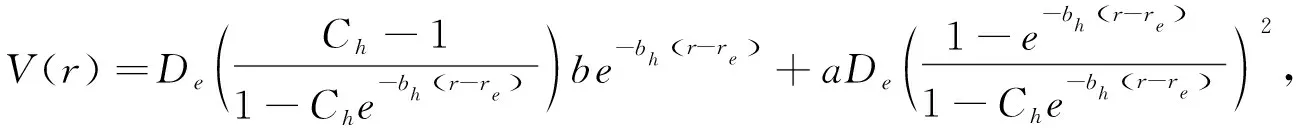
(1)
其中,De是离解能,re是平衡键长,Ch为优化参数,a,b为势常数(调整参数),bh=β(1-Ch),β为Morse常数。改进的Tietz-Hua势场添加了调整参数,应用范围更加广泛。 当参数a=1,b=0时,改进的Tietz-Hua势场退化为标准Tietz-Hua势场,对于b=0,a=1,Ch=e-bhre,bh=α,改进的Tietz-Hua势场退化为Morse势场。在文献(7)、(8)中,ONATE研究了该势场的束缚态解析解,验证了不同分子态的能级数值较好的吻合了实验观察数据,但据了解,该势场的散射态问题还没有被讨论。本文采用Pekeris类型近似办法,求解该势场的薛定谔方程的散射态问题,研究其散射振幅的解析性质,并将计算结果与相关文献进行了比较。
1 散射态的近似解析解
带有改进Tietz-Hua势场的薛定谔方程表达式为
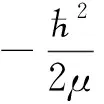
(2)
其中,E为系统本征值,设波函数为ψnlm(r,θ,φ)=r-1Rnl(r)Ylm(θ,φ),并代入(1)式化简得径向方程
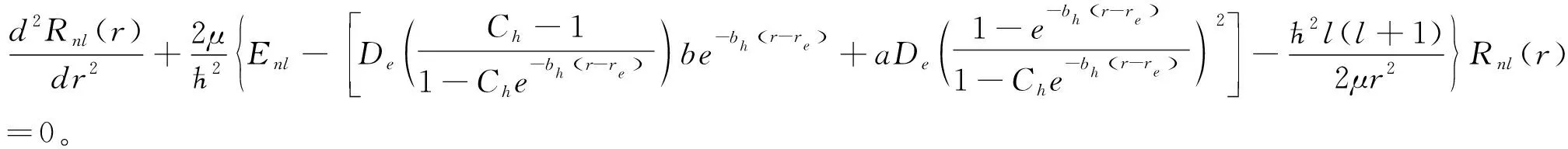
(3)
由于非线性离心项l(l+1)/r2的存在,仅当l=0时方程可解析求解,Pekeris类型的近似方法被验证是处理离心项的有效近似方法[9,10]。定义x=(r-re)/r,α=bhre,离心项可表达为

(4)
同时,离心项也可近似表达为[11]

(5)
在势函数最小值点r=re处对(5)式右侧级数展开,对比(4)和(5)近似表达式级数展开形式,可得到Pekeris类型近似表达式待定系数:
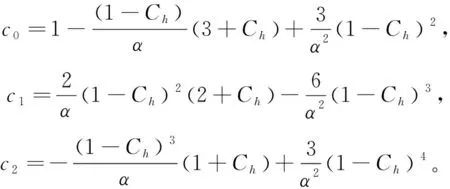
(6)
将近似表达式(5)式代入径向方程(3)式化简得

(7)
引入无刚量变量z=eax/(eax-Ch)并代入方程(7),化简得
(1-z)2z2α2R″(z)+z(1-3z+2z2)α2R′(z)+
R(z)=0。
(8)
根据波函数的边界条件z→1(r→∞),设径向波函数的形式为
R(z)=(1-z)-ik/αzηF(z),
(9)
其中参数

(10)
将所设波函数形式(9)式代入(8)式,可得如下超几何方程
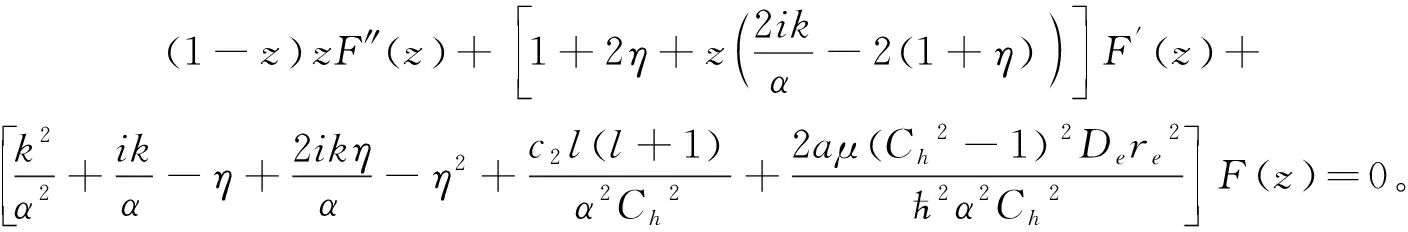
(11)
F(z)的解可用超几何函数表示为

(12)
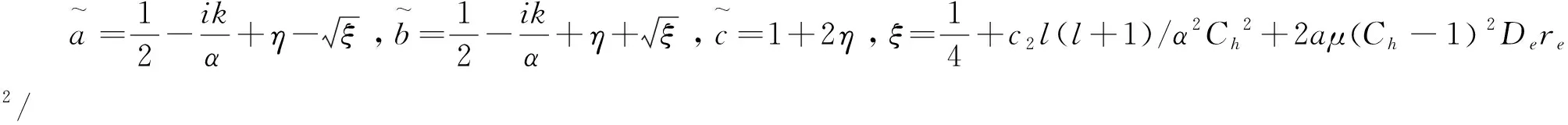
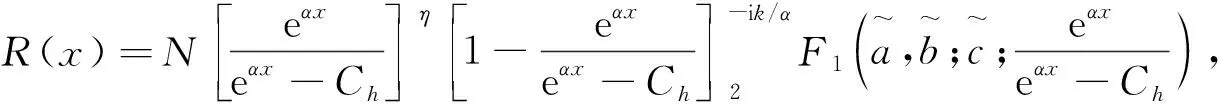
(13)
式中N为归一化常数。
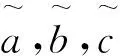

(14)
利用超几何函数的变换公式[12]

(15)
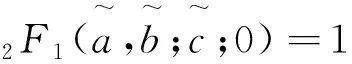
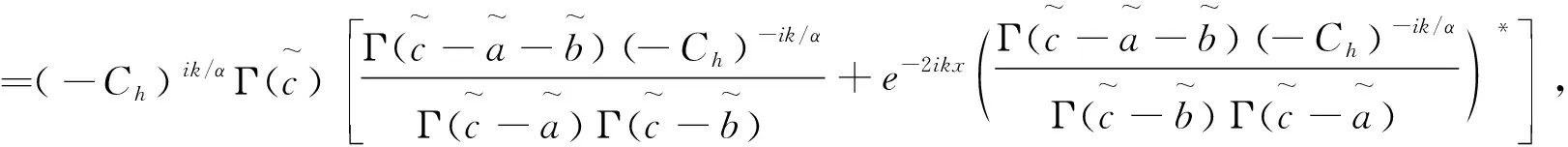
(16)
同时
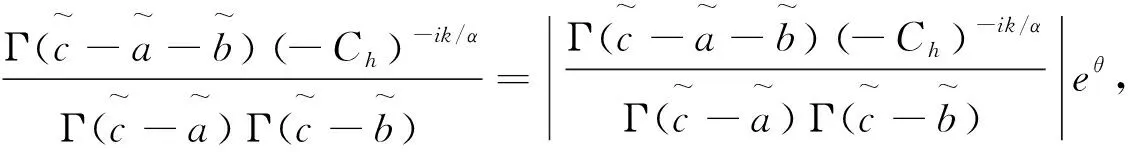
(17)
将(17)式代入(16)式得

(18)
结合公式(13),径向波函数可表示为

(19)
比较(19)式和波函数的渐进行为R(x)→2sin (kx-lπ/2+δl)(r→∞)[13],相移可表示为
(20)
众所周知,束缚态的分立能级相应于散射幅的单极点。进一步,散射振幅可表示为
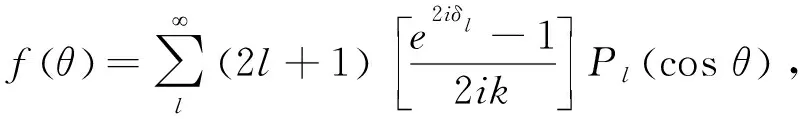
(21)
散射振幅作为能量的函数,其解析延拓到整个复平面上[14],考虑伽马函数在整个复z平面上不为零,利用伽马函数变换公式

(22)
其中,z=0,-1,-2,-3…是Γ(z)的极点,因此,表示为超几何函数的波函数渐近行为也取到极点0,-1,-2,-3,…,即
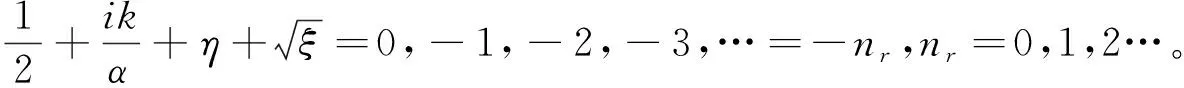
(23)
结合方程(6)、(10),解析求解方程(23),得到改进的Tietz-Hua势场的薛定谔方程本征值满足的方程:

(24)

2 讨论
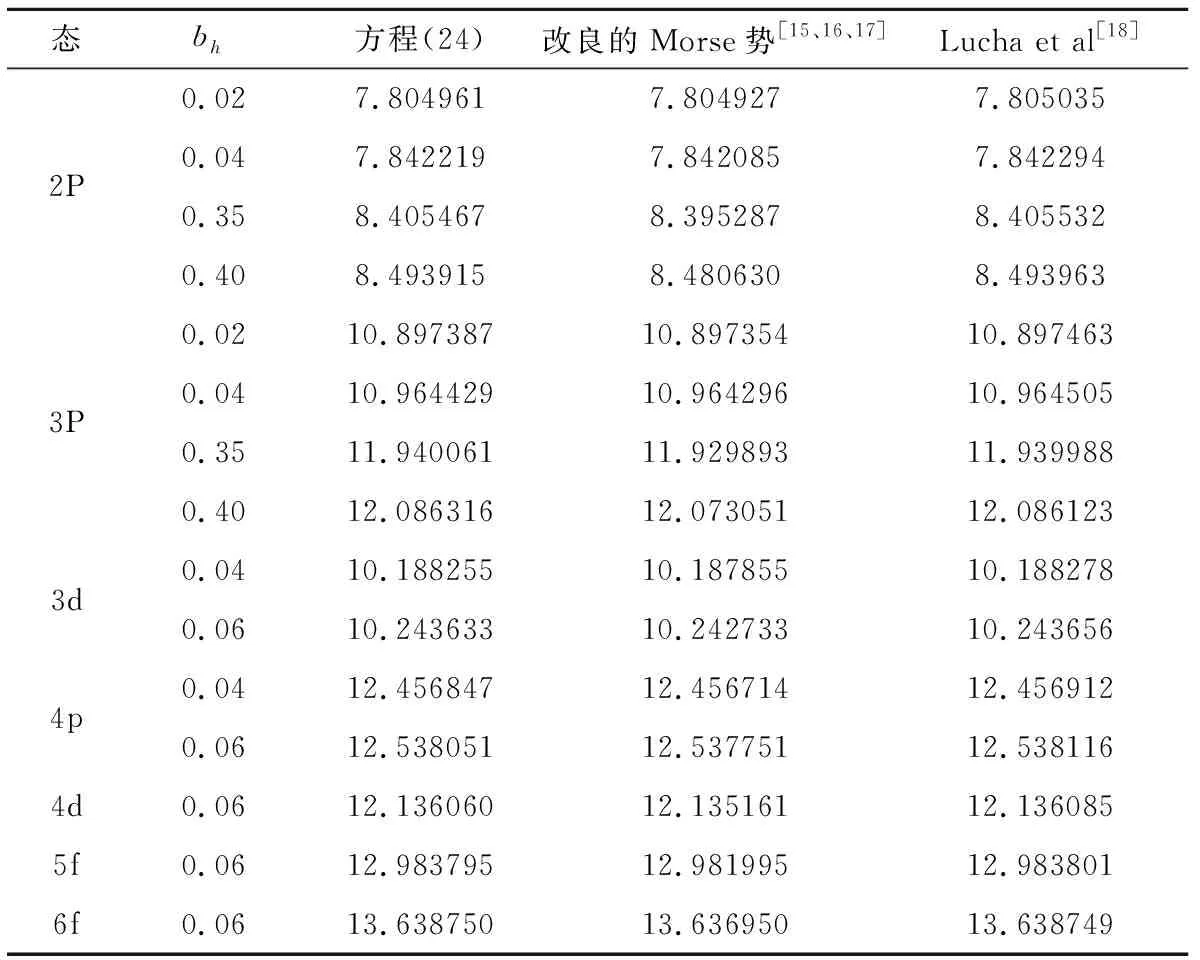
首先,优化势参数a,b取不同的值,改进的Tietz-Hua势函数可以变形为不同的势函数,以势参数a,b分别为变量,讨论其对本征值的影响。取De=10,a=0.9,b=0.01,bh=0.3,Ch=0.6,ћ=1,μ=1,图1为参数a对于本征值E的影响变化曲线,从曲线变化趋势分析,在不同态中,本征值E随着参数a的增大而增大。图2为参数b对于本征值E的影响变化曲线,在2P态情况下,当-3.61874 图1 优化参数a对特征值影响的变化曲线Fig.1 The change curve of the influence of optimization parameter a on the eigenvalue 图2 优化参数b对特征值影响的变化曲线 (25) 表1 改进的Tietz-Hua势场与改良的Morse势场所对应的本征值数值对比情况(De=15,re=0.4,a=1,b=0,Ch=e-bhre)Table 1 Comparison of eigenvalue values between the modified Tietz-Hua potential and the modified Morse potential(De=15,re=0.4,a=1,b=0,Ch=e-bhre) 表2 改进的Tietz-Hua势场与其退化后的势场本征值对比情况(De=10,re=1.6,Ch=0.6,bh=0.3)Table 2 Comparison of eigenvalue values between the modified Tietz-Hua potential and its degenerated potential(De=10,re=1.6,Ch=0.6,bh=0.3) 在表2中,文献(7)和文献(19)中的能级方程表达式中含有量子数的倒数,量子数等于零时,不能得到相应的本征值数据,进一步验证了本文解析解推导的正确性和有效性。 最后,取势参数De=10,a=0.9,b=0.01,bh=0.3,Ch=0.6,ћ=1,μ=1,数值求解了任意l态的本征值,并和MATHEMATICA程序包所得数据进行对比,本文所得数据较好的逼近真实值,见表3。 表3 特征值数值解Table 3 Numerical results of eigenvalues 散射态在量子物理还是核物理中都是非常重要的问题,本文采用Pekeris类型的近似办法处理非线性离心项,解析求解含优化参数的改进Tietz-Hua势场的薛定谔方程散射态问题,研究了该势场的散射振幅的解析性质,利用散射态的能级与散射振幅极点的束缚态的能级之间的关系,推导出束缚态能级方程。同时,为了研究优化参数对于能级的影响,绘制了优化参数与能级的变化曲线,给出不同值的优化参数情况下获得的能级数据与退化后的已求解的模型数据进行对比,进一步给出了任意l态本征值的数值解,并和MATHEMAICA程序包计算的真实值对比,自洽的验证本文推导的正确性。


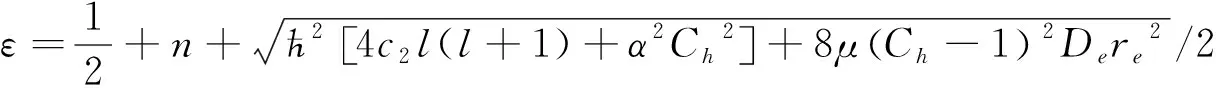


3 结论
