带有退化、拒绝和不可用区间的恒速机排序
2021-08-17赵玉芳富晓双
赵玉芳,富晓双,田 野
(1.沈阳师范大学 数学与系统科学学院,沈阳 110034;2.北京市第五中学通州校区,北京 101100)
0 引 言
Gupta和Gupta[1],Browne和Yechiali[2]分别提出了退化的概念,工件j的实际加工时间是aj+bjt(bj>0),aj是工件j的基本加工时间,bj是退化率,t是开始加工时间。以上都证明了对于最大完工时间问题,工件按aj/bj不减顺序排列可以得到最优解。Mosheiov[3]研究了极小化总完工时间的问题,工件j的实际加工时间为a+bjt,其中a是基本加工时间。进一步,对于简单的线性退化工件[4],分别提出了多项式时间算法来求解极小化最大完工时间、流程时间等问题。Ji和Cheng[5]对带有退化工件的平行机排序问题进行了研究,目标为极小化总完工时间,利用文献[6]的研究方法,给出了一个FPTAS。
Bartal等[7]首先考虑了带有拒绝的多处理机排序问题,目标函数是接受工件的最大完工时间与拒绝工件的总惩罚之和。对于离线问题,当m固定时,给出了一个FPTAS。Engels等[8]研究了带有拒绝的单机排序问题来极小化接受工件的总加权完工时间与拒绝工件的总拒绝惩罚之和,证明了其是NP-难的,并给出了动态规划算法和FPTAS。Cheng和Sun[9]考虑了带有退化和拒绝的单机排序问题,目标函数为接受工件的最大完工时间与拒绝工件的总拒绝惩罚之和,证明了该问题是一般NP-难的,给出了拟多项式时间的动态规划算法。Li和Yuan[10]讨论了同速机排序问题,当机器数固定时,给出了FPTAS。Zhao和Luo[11]研究了恒速机排序问题,给出了一个FPTAS。文献[12-13]也对带有退化和拒绝的问题进行了讨论。
Zhao和Tang[14]研究了带有退化和不可用区间的平行机排序问题,目标是极小化总加权完工时间,对于只有一台机器上有不可用区间的特殊情况,给出了一个FPTAS。Zhang和Luo[15]研究了带有退化工件、拒绝及不可用区间的2台同速机排序问题,目标为极小化接受工件的最大完工时间与拒绝工件的总拒绝惩罚之和,并提出了FPTAS。
本文考虑带有退化工件、拒绝及一台机器带有一个不可用区间的2台恒速机排序问题,目标是极小化接受工件的最大完工时间与拒绝工件的总拒绝惩罚之和。对于这个问题,给出了一个FPTAS。
1 问题描述
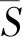
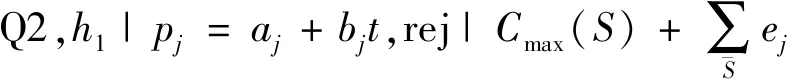
(1)
2 目标函数

1)工件在机器M1上T1之前加工的完工时间为
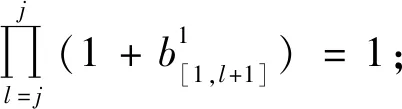
2)工件在机器M1上T2之后加工的完工时间为
3)工件在机器M2上加工的完工时间为
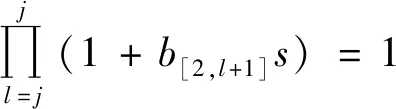
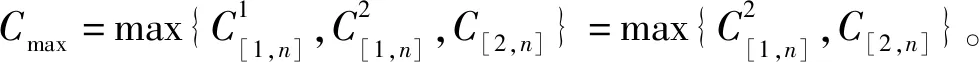
3 FPTAS
Liu等[16]证明了问题Qm|pj=aj+bjt|Cmax是NP-难的,因此问题(1)也是NP-难的,当不考虑拒绝与不可用区间时,问题1|pj=aj+bjt|Cmax按{aj/bj}不减顺序排序工件是最优的[1],因此有以下引理。
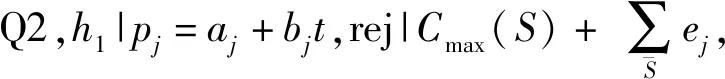
对于变量xj(j=1,2,…,n),如果Jj在机器M1的T1之前加工,令xj=1;如果Jj在机器M1的T2之后加工,令xj=2;如果Jj在机器M2上加工,令xj=3;如果Jj被拒绝,令xj=0。令X为所有向量x=(x1,x2,…,xn)的集合,其中xj∈{0,1,2,3}(j=1,2,…,n)。定义X上的递归函数如下:
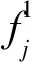
下面介绍由Kovalyov和Kubiak[6]给出的过程划分(A,h,δ),A∈X,h(x)是X上的一个非负整数函数且0<δ≤1,下面给出过程划分(A,h,δ)的步骤。
过程划分(A,h,δ)
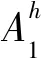
h(x(i1))≤(1+δ)h(x(1)),h(x(i1+1))>(1+δ)h(x(1))
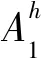
以上过程划分(A,h,δ)需要O(|A|log|A|)时间,下面的过程划分(A,h,δ)的主要性质将在本文FPTAS中使用。
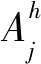
引理3[6]kh≤logh(x(|A|))/δ+2,这里h(x(|A|))≥1,0<δ≤1。
引理4 (1+x/n)n≤1+2x,对于任意0 算法Aε 步骤3 (求解)选择向量x0∈Yn满足 定理对于问题(1),算法Aε在O(n6L4/ε3)时间内找到一个解x0∈X使得F(x0)≤(1+ε)F(x*)。 令δ1=δ,考虑 因此,有 也就是 类似地,|gj+1(x*[j+1])-gj+1(x(a1,a2,a3,b))|≤(δ+δ1(1+δ))gj+1(x*[j+1])。 令δk=δ+δk-1(1+δ),k=2,3,…,n-j+1,那么有 对j+2,j+3,…,n重复论证,有x′∈Yn使得 又通过引理4,有 因此,当i=1,2,3时,可以得到 综上所述有 因此,在算法Aε的第3步中,向量x0被选择满足F(x0)≤F(x′)≤(1+ε)F(x*)。 本文研究的是带有退化工件、拒绝和一个固定的不可用区间的2台恒速机排序问题。目标函数是接受工件的最大完工时间与拒绝工件的总惩罚之和。本文根据Kovalyov和Kubiak[9]的过程划分的方法给出了一个FPTAS,确定了其时间复杂性为O(n6L4/ε3)。由于机器带有不可用区间以及拒绝惩罚同时存在的现象很普遍,因此,进一步研究机器带有不可用区间以及拒绝惩罚的排序问题具有广泛的应用价值和实际意义。对于具有其他退化效应的函数问题以及机器具有不可用区间的其他种类机器的排序问题,有待进一步研究。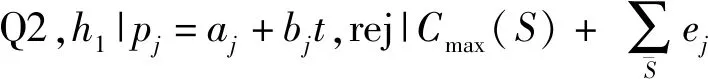
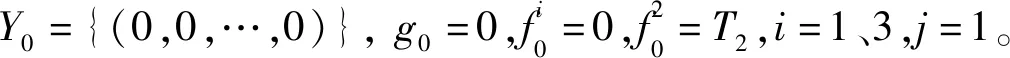

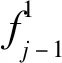
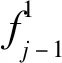
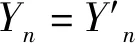
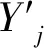
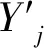
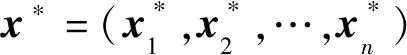
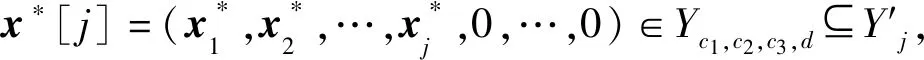
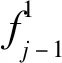


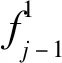




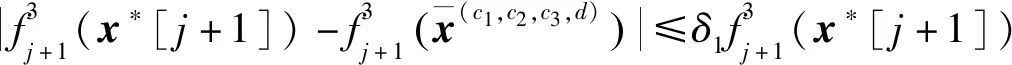

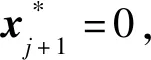
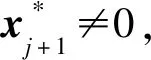
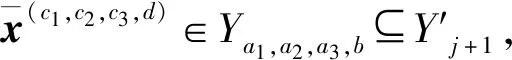
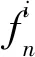
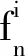

4 结 论
