光子纠缠态在non-Kolmogorov大气湍流中纠缠退化的研究

张钦伟,曹连振,刘霞,杨阳,赵加强,李英德

(潍坊学院物理与光电工程学院,山东省高校多光子纠缠与操纵重点实验室,山东 潍坊 261061)

0 引言

由量子力学与信息科学交叉融合形成的量子信息在保密通信、超快计算、精密测量及成像等方面具有得天独厚的优势,量子纠缠作为量子信息的一种重要资源可广泛用于量子通信[1]、量子计算[2]、量子精密测量[3],以及研究量子物理基础问题。目前,基于非线性晶体自发参量下转换过程制备纠缠态是比较成熟的技术,该技术可以实现时间-频率、偏振、路径、轨道角动量等多个自由度纠缠,中国在该领域一直处于领先地位,相继实现了10光子纠缠[4]和6光子18比特纠缠[5]、32比特高维纠缠[6]和100维路径集成纠缠[7]。非线性晶体的自发参量下转换过程满足动量守恒,因此高斯泵浦光在非线性晶体自发参量下转换产生空间分离的“信号光子”和“闲置光子”路径是关联的,所以常用路径自由度来定位收集纠缠光子。“京沪保密干线”的开通和“墨子号”量子科学实验卫星成功完成星地之间三大典型量子通信方案(量子密钥分发、量子隐形传态、量子纠缠分发),标志着量子通信已初步迈向实用化阶段。但是,星地间量子通信经过大气层时,由于空间温度、压强、密度等因素变化会导致大气空间折射率随机起伏,必会引起量子光场的波前畸变和振幅起伏,使得量子比特的相位趋向无规则化,进而会导致纠缠退化产生误码。由于湍流介质具有随机性,且介质折射率随机起伏较弱,因此处理光场在湍流介质中的传输问题常采用统计-微扰近似的方法。光场在湍流介质中的光学空间统计特性既可以由结构函数和相干函数解析描述,又可以由相位屏仿真模拟[8,9]。针对偏振纠缠态、路径纠缠态以及轨道角动量纠缠态在各向同性的Kolmogorov大气湍流中的纠缠退化、相位起伏、光强闪烁等问题进行了相关报道[10-19],相应纠缠保护、纠错方案也相继提出[18]。但是Kolmogorov大气湍流折射率功率谱只能描述各向同性的惯性区,不能完全描述大气湍流的统计规律。为了更好地描述大气湍流的统计规律,Toselli等[20]提出non-Kolmogorov折射率功率谱,该大气湍流统计模型可描述大气对流层、平流层等,适用范围更广,更接近真实湍流环境。双量子比特路径光子纠缠态在Kolmogorov大气湍流传输过程中的退相干问题虽被研究[10],但是双量子比特路径纠缠态在更为复杂的non-Kolmogorov大气湍流传输过程中退相干问题研究甚少,但后者更具有实际意义。

本文基于量子化光场和大气湍流相位结构函数统计近似处理方法,研究了双量子比特路径纠缠态在non-Kolmogorov大气湍流下的纠缠退化问题。通过建立物理模型,得到了双量子比特路径纠缠态在non-Kolmogorov大气湍流中纠缠退化的解析表达式,并在此基础上进行了数值仿真,定量分析了各种影响因素。研究结果表明:双量子比特路径纠缠态在大气信道中传输退化程度受大气湍流环境和纠缠光子对空间分布双重因素的制约,该研究为自适应远距离低误码率的量子通信提供了理论参考。

1 理论分析

通常认为大气由层流和湍流两种运动所组成,由于气体的运动粘滞度很小,其运动状态几乎每时每刻都处于折射率随机起伏的湍流状态。大气空间折射率随机起伏主要是由空间温度、密度和压强的不均匀性造成的。描述接近实际湍流大气运动状态的物理模型non-Kolmogorov折射率功率谱可通过对大气空间折射率自相关函数的傅里叶变换修正得到,其形式可表示为[20-22]

图1 双量子比特路径纠缠态在湍流大气中传播示意图Fig.1 Schematic of spatial two-qubit states propagation through atmospheric turbulence

为了制备高关联性的双量子比特路径纠缠态,两对闲置光子和信号光子小孔分别设置在对称的位置,即ρs1=-ρi1和ρs2=-ρi2。因此,双量子比特路径纠缠态在non-Kolmogorov大气湍流中传输的共生纠缠度可表示为

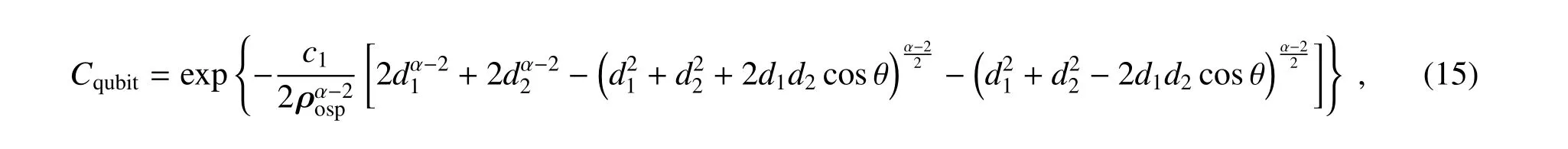
式中双量子路径纠缠态的空间物理尺度d1=|Δ(ρs1-ρi2)|,两个闲置小孔和信号小孔之间的距离d2=|Δ(ρs1-ρi2)|,θ为 (ρs1-ρs2)与 (ρs1-ρi2)之间的夹角。

2 数值计算与分析

本节采用数值仿真的方式分析了双孔实验装置与大气湍流等各种影响双量子比特纠缠态纠缠退化的因素。

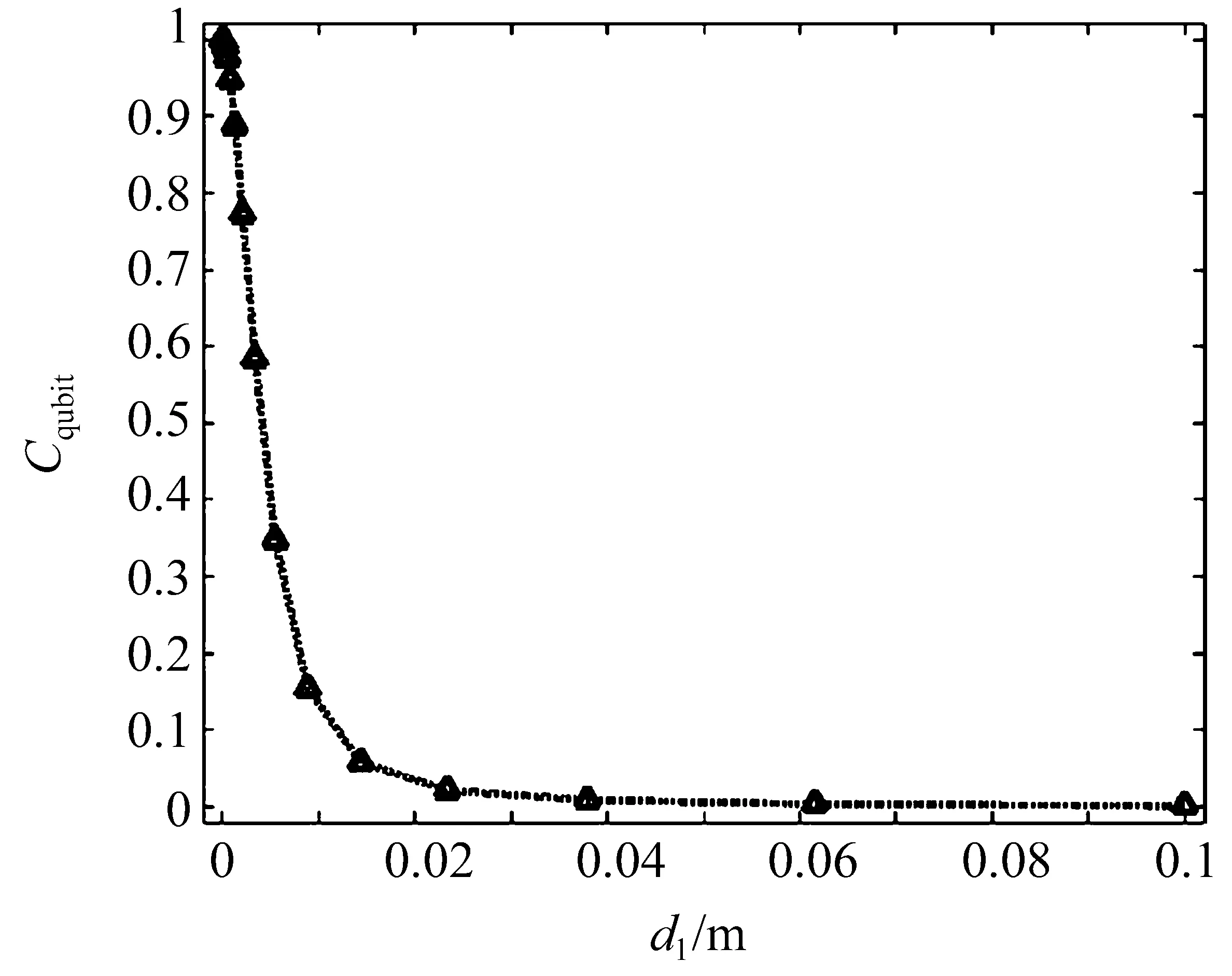
图2 Cqubit随d1的变化Fig.2 Change of Cqubitwith d1

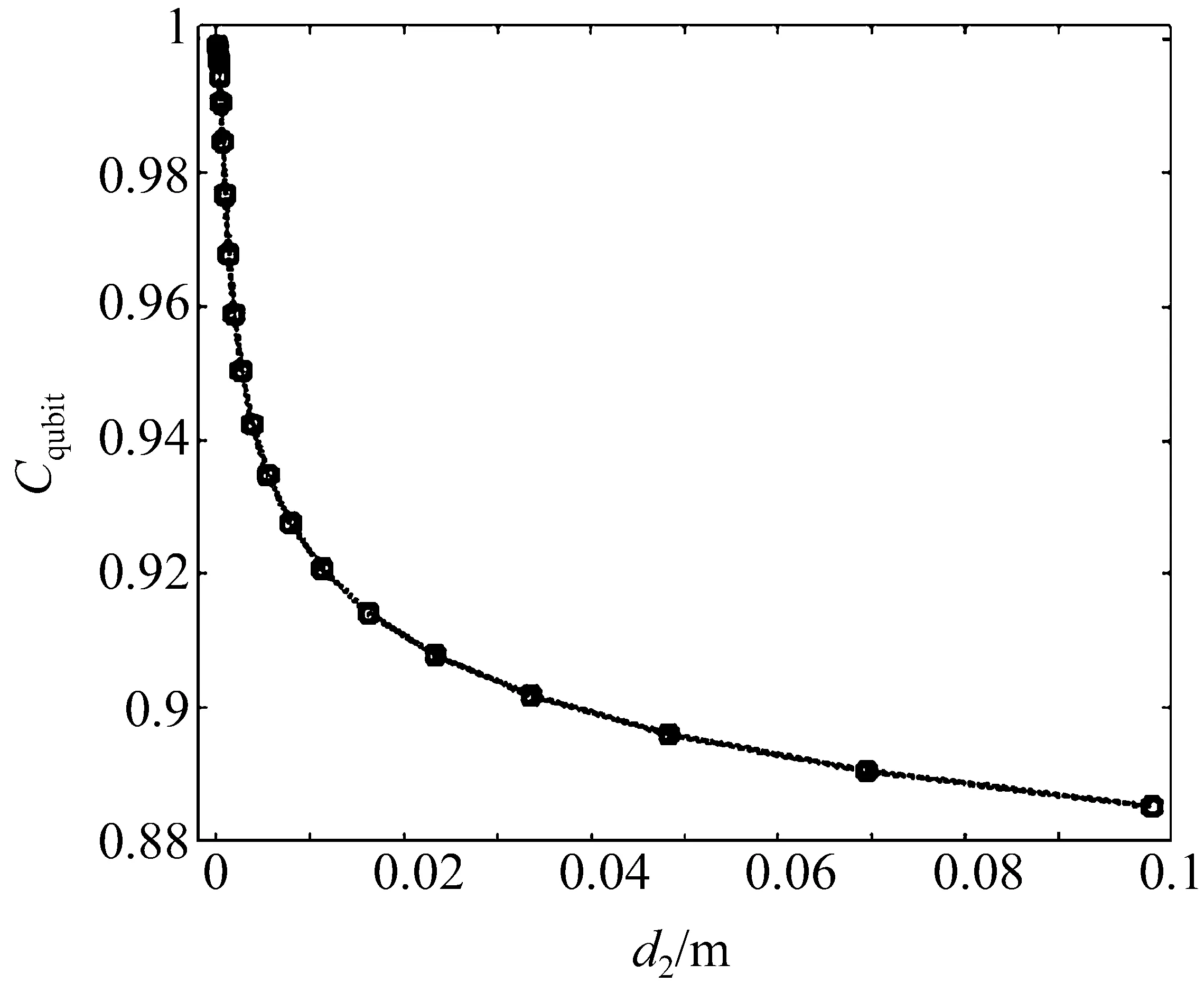
图3 Cqubit随d2的变化Fig.3 Change of Cqubitwith d2

为了进一步挖掘双孔系统实验装置与双量子比特路径纠缠态纠缠退化的关系,数值分析了在下,θ分别为 π/6、π/4、π/3时Cqubit随传输距离z的变化,如图4所示。由图可见,随着z的增加,Cqubit与θ的关系更明显,θ较大时,双量子比特路径纠缠态抗干扰能力相对好一些。

图4 不同θ情况下Cqubit随z的变化Fig.4 Change of Cqubitwith z under different θ

图5 不同λ情况下Cqubit随z的变化Fig.5 Change of Cqubitwith z under different λ

为了进一步发现大气湍流效应对纠缠态退相干的影响,分析了双量子比特路径纠缠态在不同折射率功率谱指数、广义湍流折射率结构起伏结构函数下的退化情况,模拟结果如图6所示。图6(a)分析了分别为3.1、3.6、3.9时Cqubit随z的变化。当α较大时,Cqubit依然保持较高,特别是在α=3.9的大气湍流中传输104m后,Cqubit可保持在0.75左右,这要比在Kolmogorov大气湍流(α=11/3)情况下纠缠度高。图6(b)展示了λ=780 nm、α=3.6、d1=0.001 m、d2=0.1 m、θ=π/4,广义湍流折射率结构起伏结构函数分别为5×10-15、1×10-15、1×10-16m3-α时Cqubit随z的变化。由图可见,对Cqubit的影响很明显,双量子比特路径纠缠态在传输相同的距离104m后,=10-15m3-α增大到=10-16m3-α时,Cqubit将由0.5左右降到0附近。通过图6可推断出随着大气湍流起伏波动增强,双量子比特路径纠缠态的相位起伏程度将进一步增大,纠缠度也会进一步降低。综上所述,大气湍流效应对纠缠态的影响很明显,需要高度重视。该研究将为自适应量子通信或量子通信纠错控制提供一定的理论指导。

图6 (a)不同α情况下Cqubit随z的变化;(b)不同C˜n2情况下Cqubit随z的变化Fig.6(a)Change of Cqubitwith z under different α;(b)Change of Cqubitwith z under different

3 结论

以自发参量下转换制备的双量子比特路径纠缠态为研究对象,分析了其在具有普适性的non-Kolmogorov大气湍流传输过程中的退相干问题。基于non-Kolmogorov大气湍流和共生纠缠度度量方法,得到了双量子比特路径纠缠态在non-Kolmogorov大气湍流中纠缠退化的解析表达式。为进一步挖掘具备抗噪特性的纠缠态以提高量子通信的成码率、降低误码率,分析了双孔实验系统和大气湍流效应对纠缠态的影响。研究结果表明:双孔实验系统存在影响双量子比特纠缠态退相干的因素,双孔的物理尺度和小孔间距随着大气湍流的起伏扰动增强,纠缠态的纠缠度会进一步降低,且随着传输距离增加,其退相干问题更严重。根据所建立的物理模型,得到的纠缠退化解析表达式可以定量分析纠缠退化问题,为自适应低误码率的远距离大气量子通信提供了可靠的理论参考。