基于微分博弈的移动目标防御最优策略

孙 岩 姬伟峰 翁 江 赵蓓英

(空军工程大学信息与导航学院 西安 710077)

日益严重的信息安全事件对网络空间造成巨大威胁，易攻难守是当前网络安全面临的核心问题之一[1].为增强网络防御能力，确保网络空间安全[2]，美国科学技术委员会提出了移动目标防御(moving target defense, MTD)技术，该技术是改变攻击和防御不对称状态的新方法，目的在于强化信息系统多样性、动态性和随机性的特征，增大攻击成本，提高抗攻击能力.但滥用MTD技术并不会提高防御能力，反而会增大防御成本、降低系统利用效率[3].如何科学决策移动目标防御行为已成为亟待解决的问题.网络空间对抗所展现出来的目标独立性、策略依存性和非合作性与非合作博弈理论的特征基本一致.目前已有学者运用博弈论分析网络空间攻防行为，开展移动目标防御决策研究.

网络攻防博弈中，当攻防双方均采用各自的最优策略时，二者无法通过独自偏离其最优策略得到更多收益，即认为攻防双方为理性决策者.在此条件下，运用于网络攻防策略选取研究中共有经典博弈、Markov博弈和微分博弈3种模型[4].

在经典博弈模型中，根据网络攻防双方信息是否透明、攻防行为是否同步、攻防博弈阶段是否单一，分别可以采用完全信息模型[5]与不完全信息模型[6]、静态模型与动态模型[7]、单阶段模型与多阶段模型[8].当进一步考虑攻防行为信息对攻防行为产生的影响时，可引入信号博弈模型.本文作者在文献[3]中考虑防御者自身系统存在无法避免的缺陷下，利用信号博弈模型提出移动目标防御最优策略选取算法与最优诱导信号算法，研究了不完全信息下动态多阶段的MTD策略选取问题.

在Markov博弈模型中，决策者认为过去的攻防行为会对现在及未来的攻防行为决策产生影响.文献[9]利用多目标Markov决策过程对攻击者和防御者之间的相互作用进行建模，设计一种有效的基于移动目标变换的DDoS攻击防御方案.文献[10]将网络漏洞的利用抽象为攻击面和探测面的变化，提出完全信息Markov博弈最优策略选择方法，但完全信息的假设不适用于未知漏洞下的网络对抗.文献[11]以文献[10]为基础提出了一种不完全信息Markov博弈方法IIMG-MTD来生成移动目标防御策略.

随着网络技术的不断发展，网络对抗过程逐渐具有动态性、连续性和实时性.经典博弈模型与Markov博弈模型均为时间离散博弈模型，以上工作只能分析单阶段攻防过程或时间离散的多阶段攻防过程，难以满足移动目标防御策略的时效性要求.因此，部分文献利用微分博弈理论进行网络攻防相关研究.文献[12]对连续时间的网络攻防过程进行研究分析，针对威胁预警需求，提出网络攻防定性微分博弈模型，构造攻防界栅以划分捕获区及躲避区，引入多维空间欧氏距离评估威胁程度，确定安全状态所处威胁预警等级并根据预警等级对网络防御提出针对性建议.但该文献未考虑攻防过程中的攻防目标收益，在成功预测威胁等级后无法针对攻击行为选取最优防御策略以最大化防御效益.文献[13]对连续过程中的网络攻防行为进行分析研究，借鉴传染病动力学理论构建了攻防微分博弈模型，提出了鞍点策略的求解方法和最优防御策略选取算法.但该文献仅分析了网络空间安全状态的宏观变化过程，未对网络内部的微观节点行为进行合理建模，导致无法针对网络内部某些关键节点量身定制防御策略.文献[14]探讨了如何合理地将可用的修复资源分配给可能不安全的主机，以减轻网络的潜在损失，基于一种新的期望状态演化方程，构建高级可持续威胁(advanced persistent threat, APT)响应微分博弈模型，提出了一种寻找APT修复博弈潜在纳什均衡算法.以上文献均基于微分博弈做出网络防御决策响应，但未能与MTD紧密结合.

考虑到网络内部微观个体行为与宏观传播现象之间的相互依赖会对网络攻防决策产生影响，本文利用节点级传染病理论方法构建基于微分博弈的MTD决策模型，分析网络攻击与MTD实时变化条件下的网络系统个体的安全状态演化过程，提出攻防策略决策函数与目标收益函数.通过设计该微分博弈模型的开环纳什均衡算法，得到最优MTD防御策略实时结果.

1 预备知识

1.1 微分博弈的概念与模型

微分博弈是时间连续的动态博弈，在n个参与者的微分博弈中，每位参与者i(i∈Γ={1,2,…,n})的目标函数可以表示为

(1)

其中，x(τ)∈X⊂m为博弈的状态变量或状态(X为状态空间)，这种变量在非微分博弈中是不存在的.ui(τ)∈Ui为参与者i的策略(Ui为策略空间)，但与非微分博弈中的策略不同，因为它代表一条随时间发展的策略路径.

τ∈[t0,tf]代表博弈的每一个时间点或者时刻，t0和tf分别为博弈的开始时刻和结束时刻，gi[τ,x(τ),u1(τ),…,un(τ)]≥0和qi[tf,x(tf)]≥0分别表示参与者i的瞬时支付与终点支付.

在式(1)中，状态变量x(τ)的进展变化取决于一个确定性动态系统，即

(2)

1.2 微分博弈的纳什均衡

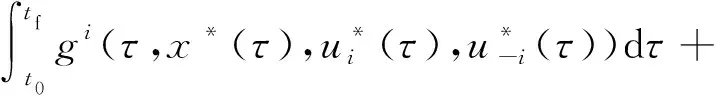
(3)

而在时间区间[t0,tf]中，有

(4)

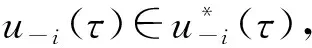
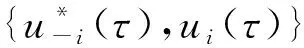
证毕.

2 MTD微分博弈

2.1 网络基础状态

现实中，网络内部主机状态是时变的，考虑带有数据库服务器和N个主机的网络，如图1所示.其中双箭头实线表示主机之间可以进行正常交互，双箭头虚线表示主机与数据库服务器之间的正常数据流，单箭头虚线表示已连接但未画出的其他主机.

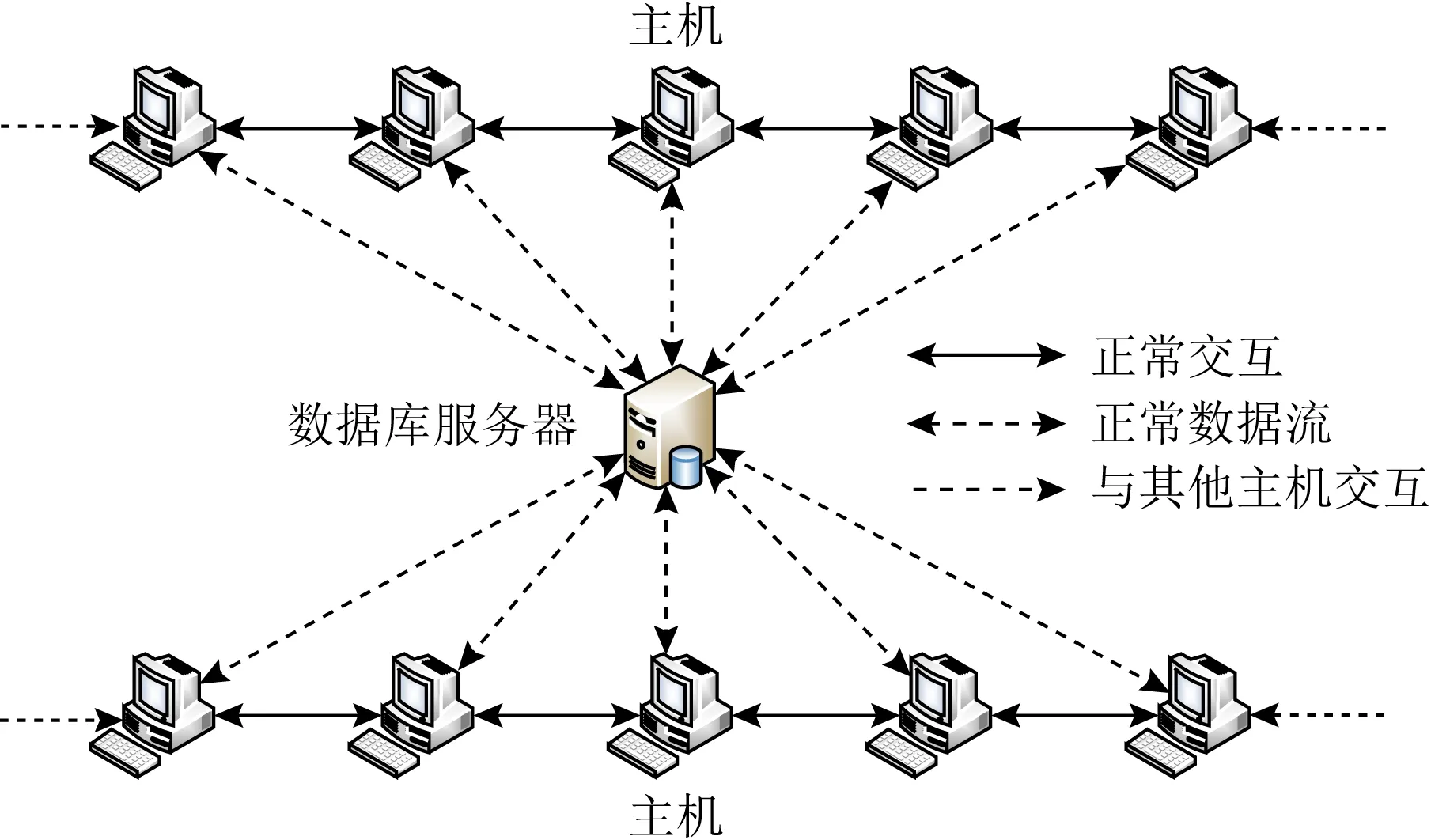
Fig. 1 Network topology图1 网络拓扑结构

定义1.网络基础状态模型(basic state model)MBS.可以表示为

MBS={τ,b(τ),R(τ),Xi(τ),Si(τ),Ii(τ)},

其中，τ代表攻防微分博弈的时刻，τ∈[t0,tf].

b(τ)=(b1(τ),b2(τ),…bN(τ))表示主机i在时刻τ的工作状态，bi(τ)=0或1表示主机i在时刻τ处于关机或开机状态.

R(τ)=(rij)N×N为网络连通状态矩阵.rij=0或1表示主机i与j不可相互通信或可以相互通信，规定rii=0.令cij(τ)=rijbi(τ)bj(τ)，根据定义1可知，当cij=1时，主机i与j可在时刻τ互相传递信息，此时攻击者的恶意攻击行为也可以进行传播，本文称之为横向攻击行为.

根据主机是否受到攻击来确定主机的状态是否安全，令Xi(τ)=0或1表示主机i在时刻τ处于安全状态或不安全状态.

利用概率表示主机i的安全状态程度，令Si(τ)=Pr{Xi(τ)=0}表示主机i在时刻τ处于安全状态的概率，Ii(τ)=Pr{Xi(τ)=0}表示主机i处于不安全状态的概率，且Si(τ)+Ii(τ)=1.

2.2 网络节点安全状态演化模型

网络攻防行为对网络空间的混合作用，造成网络节点的安全状态随着时间变化，本节对网络空间主要节点安全状态的演化过程进行建模.

定义2.网络节点状态演化模型(state evolution model)MSE.可以表示为

MSE={Θ,P(τ),C,B,MBS}.

Θ={A,D}表示攻防动作行为空间.其中，A={ax|x=1,2,…,n}，D={dy|y=1,2,…,n}分别表示攻击行为动作集与防御行为动作集.

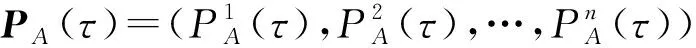
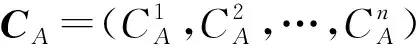
根据定义2可知，攻击者攻击主机i时，该主机将会受到来自攻击者的直接攻击和攻击者通过其他主机的发起的横向攻击.

当攻击者对主机i发起横向攻击时，会存在影响其成本与收益的传染系数，该传染系数与横向攻击的传染次数有关。令{ξ1(τ),ξ2(τ),…,ξn(τ)}表示传染系数集合，其中ξm表示当横向攻击进行m次传染时的传染系数.当横向攻击进行1次传染时，即攻击者以主机j→i顺序进行横向攻击，其传染系数为

(5)

当横向攻击进行2次传染时，即攻击者以主机k→j→i顺序进行横向攻击，其传染系数为

(6)

当横向攻击进行3次传染时，即攻击者以主机l→k→j→i顺序进行横向攻击，其传染系数为

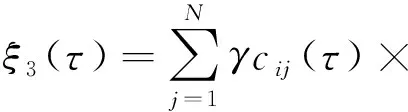
(7)

按式(5)～(7)规律可类推横向攻击传染m次时的传染系数ξm.

式(5)～(7)中，γ为传染衰减因子，表示相对于直接攻击，横向攻击的收益与代价会有一定程度的衰弱.

根据式(5)～(7)可知，该主机i状态满足以下微分演化方程：

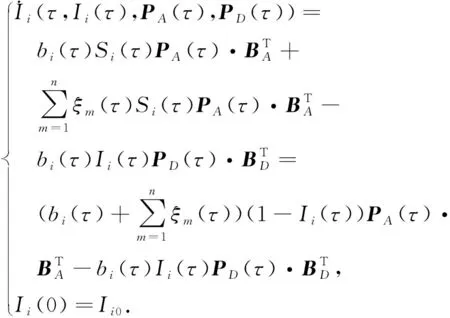
(8)

网络节点安全状态演化过程示意如图2所示：

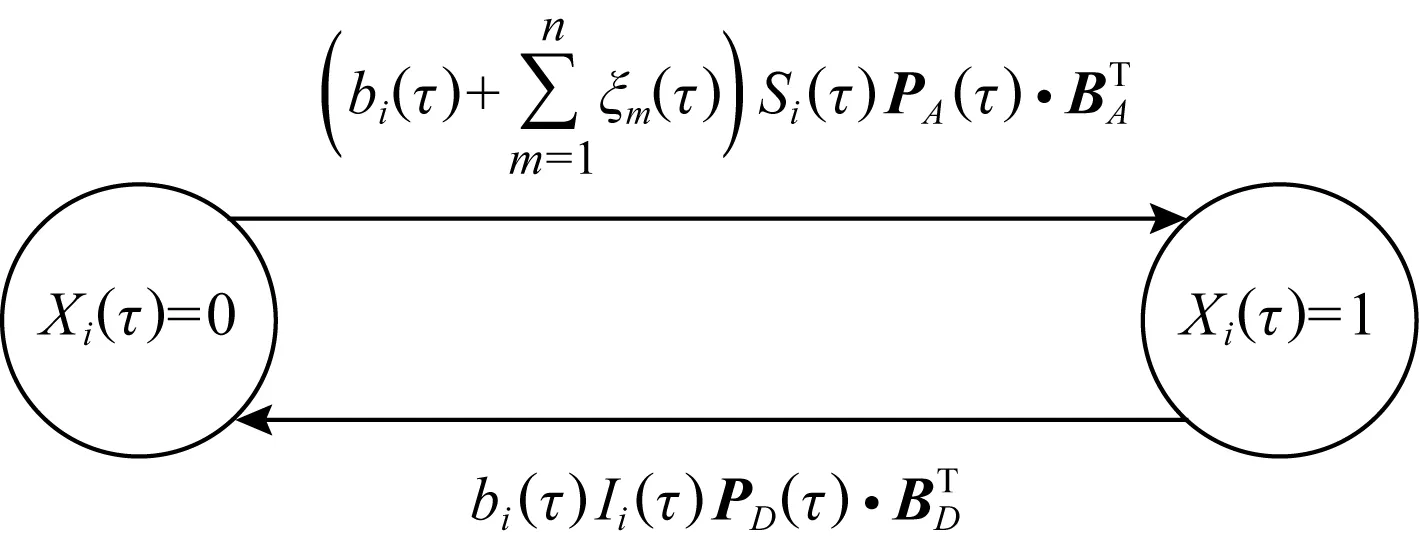
Fig. 2 Network node safe state evolution model图2 网络节点安全状态演化模型

2.3 移动目标防御微分博弈模型定义

定义3.移动目标防御微分博弈模型(moving target defense differential game model) MTDDG.可以表示为

MTDDG={Ω,G,U,MSE}.

Ω={ΩA,ΩD}为博弈人空间.ΩA为攻击者，ΩD为防御者.

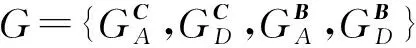
其中，在攻防持续时间内攻击者发动攻击的成本函数为

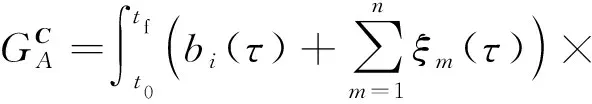
(9)

防御者启动MTD的成本函数为

(10)

在攻防持续时间内,攻击者发动攻击的收益函数为

(11)

防御者启动MTD的收益函数为

(12)

U={UA,UD}表示攻击者与防御者的收益目标函数.以主机i为例，攻击者与防御者的目标收益函数分别为式(13)(14)：

(13)

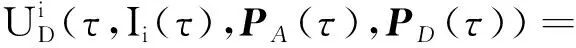
(14)

3 最优策略求解方法

3.1 MTDDG纳什均衡定义

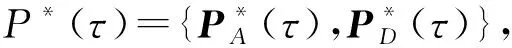
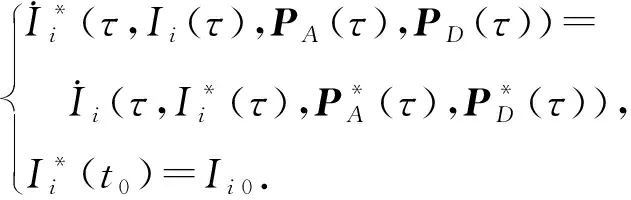
(15)

满足约束条件(式(15))的情况下，对于策略向量集合P*(τ)构成的微分博弈式(8)(13)(14)，以下不等式成立:

(16)

为易于分析处理与应用，本文选择开环纳什均衡方法求解攻防最优策略.

定理2.对于微分博弈式(8)(13)(14)，最优攻防策略集合P*(τ)构成开环纳什均衡.满足约束条件(式(12))的情况下,若存在共态函数{λA(τ),λD(τ)}:[t0,tf]→m，式(17)～(19)成立.

(17)

(18)

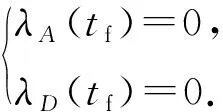
(19)

证明.受制于网络节点演化过程(式(15))，考虑式(17)中的第1个公式，即最大化攻击者目标收益

证毕.

基于定理2，为寻找该攻防系统的开环纳什均衡解，根据微分博弈理论，构建Hamiltonian函数

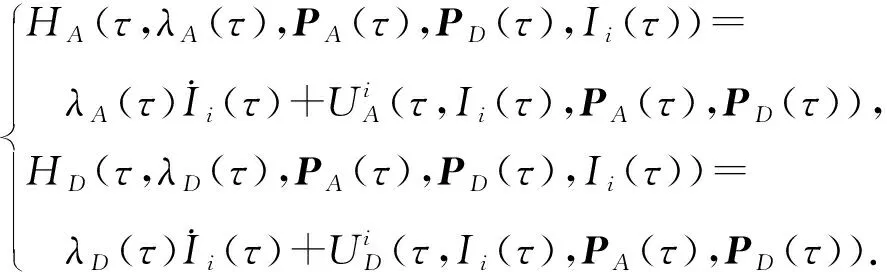
(20)

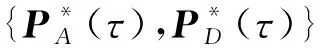
1) 满足式(19)的条件下，式(21)成立;

2) 当1≤i≤N，t0≤τ≤tf时，式(22)成立.

(21)

(22)

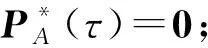
根据Pontryagin Maximum原则，当1≤i≤N，t0≤τ≤tf时，存在{λA(τ),λD(τ)}.式(21)可由式(18)(20)直接联立计算得到.

满足约束条件(式(15))的情况下，当t0≤τ≤tf时，有：

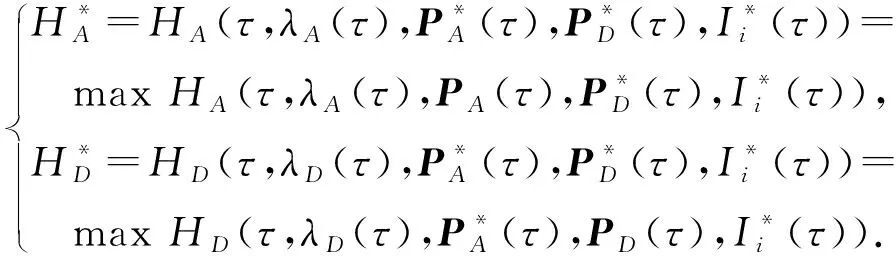
(23)

证毕.

3.2 MTDDG开环纳什均衡求解算法

针对2.1节中主机状态bi(τ)，本文将攻防持续时间分为多个较短的时间段，然后为每个短时间段以一定概率分配0或1给每一个主机.

算法1.MTDDG开环纳什均衡求解算法.

输入：{MBS,MSE,MTDDG},设置收敛误差ε=10-4，迭代次数上限K=103;

① 初始化MBS，MSE，MTDDG;

② for 1≤k≤ndo

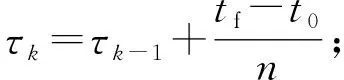
④ end for

⑤ for 1≤i≤Ndo

⑥ for 0≤k≤n-1 do

⑦ 以概率0.6令μ=1;以概率0.4令μ=0;

⑧bi(τ)μ;

⑨ end for

⑩bi(tf)=bi(tn-1);

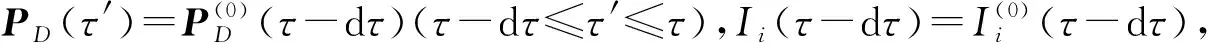
λA(tf)=λD(tf)=0后向计算λA(τ)，

λD(τ)(t0≤τ≤tf);

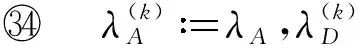
PA(τ) 和PD(τ),(t0≤τ≤tf);

或者k≥K;

不同模型之间的比较结果如表1所示.模型的时效性指模型在应用时得出结果有效持续时间.例如，单阶过程得出的结果只适用于单阶段，微分博弈模型考虑到时间因素可以实现任意时刻的决策.模型通用性指文献中的策略与动作合集是否可以扩展.

Table 1 Comparative Analysis of Models表1 模型对比分析

4 实验仿真与分析

4.1 实验环境描述

采用工具SSFNet (scalable simulation frame-work)[17]开展仿真实验.为提高仿真实验真实性，参考文献[18]，从Route Views Project中得出自治系统(autonomous system)连接数据集以设计实验网络拓扑结构，采用网络数据集NetTFDate20200126 113000构建网络场景.实验网络拓扑结构如图3所示，空心叉号表示主机处于关机状态，实心叉号表示该主机被攻击者劫持,双箭头虚线表示攻击者的命令与控制数据流和从数据库流出的被窃取数据或正常数据流,单箭头实线表示从攻击者和被劫持主机发出的攻击行为，双箭头实线表示主机之间的交互.网络节点总数共802个，其中数据库服务器节点数量1个，用户终端节点800个，攻击节点1个.设传染衰减因子γ=0.05，攻防持续时间为5 min，即τ∈[t0,tf]=[0,5].

Fig. 3 Experimental network topology图3 实验网络拓扑结构

实验中根据网络安全检测设备扫描并分析相应攻击信息，判断攻击者类型及其攻击能力，并结合国家信息安全漏洞库(CNNVD)数据[19]和文献[20]漏洞分析方法的基础上，参照美国MIT攻防行为数据库[21]以及文献[3,14,22-23]构建网络安全攻防行为集，并综合各方面安全指标计算其平均行为效用，如表2～3所示:

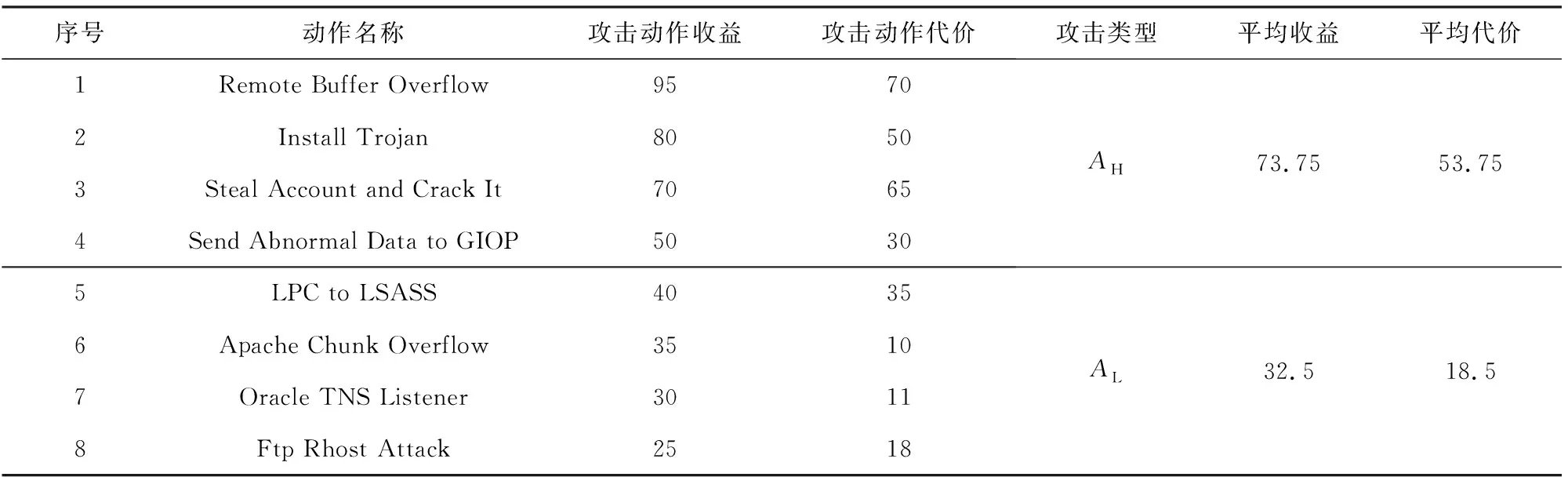
Table 2 Description of Attack Actions表2 攻击动作描述

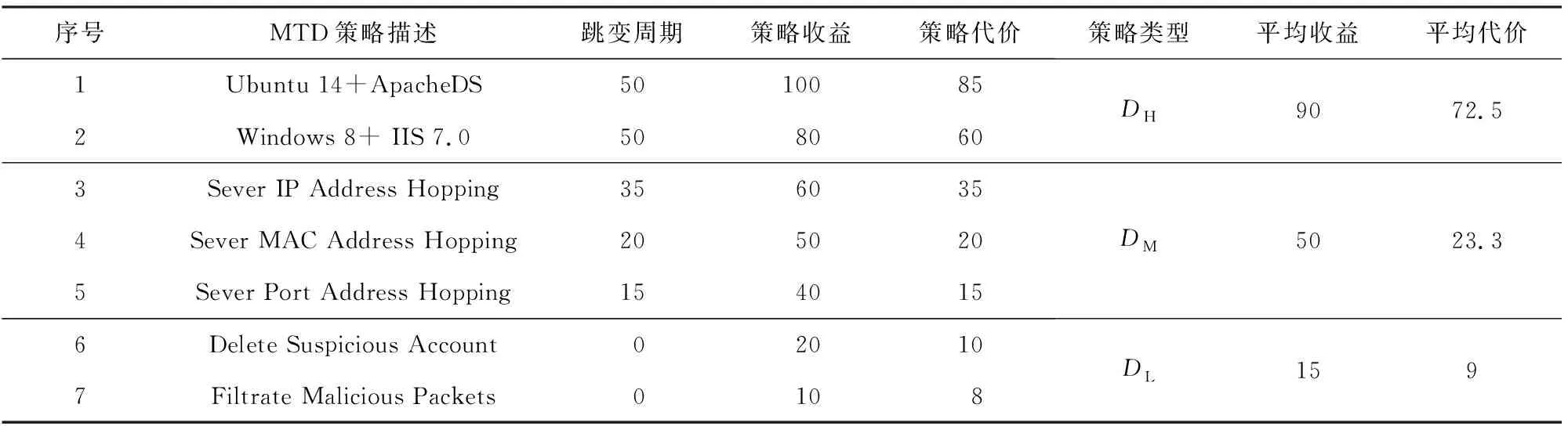
Table 3 Description of MTD and Static Defense Actions表3 MTD与静态防御动作描述

对于攻击动作行为，本文将其分为2种类型，即A={AH,AL}；对于防御动作行为，令当前数据库服务器部署的数据库服务软件栈为“Windows7 SP1+IIS 6.0”， 数据库服务器可采取的防御措施分为3种类型，即D={DH,DM,DL}.其中，DH是指通过建立一系列多态化虚拟服务器，每个数据库服务器配置唯一的软件栈，采取固定周期跳变的方式不断改变数据库服务器程序与操作系统的实现方式.DM指采取固定跳变周期方式更改数据库服务器IP地址、MAC地址和端口地址.为对比分析MTD策略与静态防御策略的差异，设置DL为采取常规静态防御方式进行网络防御.本文以网络中重要设备数据库服务器为例，考虑攻击者对数据库服务器的直接攻击以及通过对网络内部主机攻击进而横向攻击数据库服务器.作为网络系统的重要设备，假设数据库服务器始终保持开机工作状态.

本实验MTDDG最优策略算法利用Matlab 2018工具实现.考虑到随着横向攻击的传染次数的增加，传染系数中传染衰减因子成指数倍增长，当进行4次传染时，γ4=0.000 006 25.因在实验中设置收敛误差为ε=10-4，所以4次及以上次数传染对网络攻防的收益/成本影响不大，所以只考虑横向攻击的传染次数为1次、2次与3次的情况.以图3为例，横向攻击传染次数为1次、2次与3次时分别对应图中的攻击传染路径为1→4，1→2→5，1→2→3→6，该对应并不唯一.

4.2 实验分析

由实验结果得到攻击防御行为选取策略，如图4、图5所示.攻防双方采取概率混合策略，但为方便分析，认为攻防双方在不同时刻采取高概率攻防行为.

Fig. 4 Optimal policy control trajectory of attack 图4 攻击策略和的最优控制轨迹

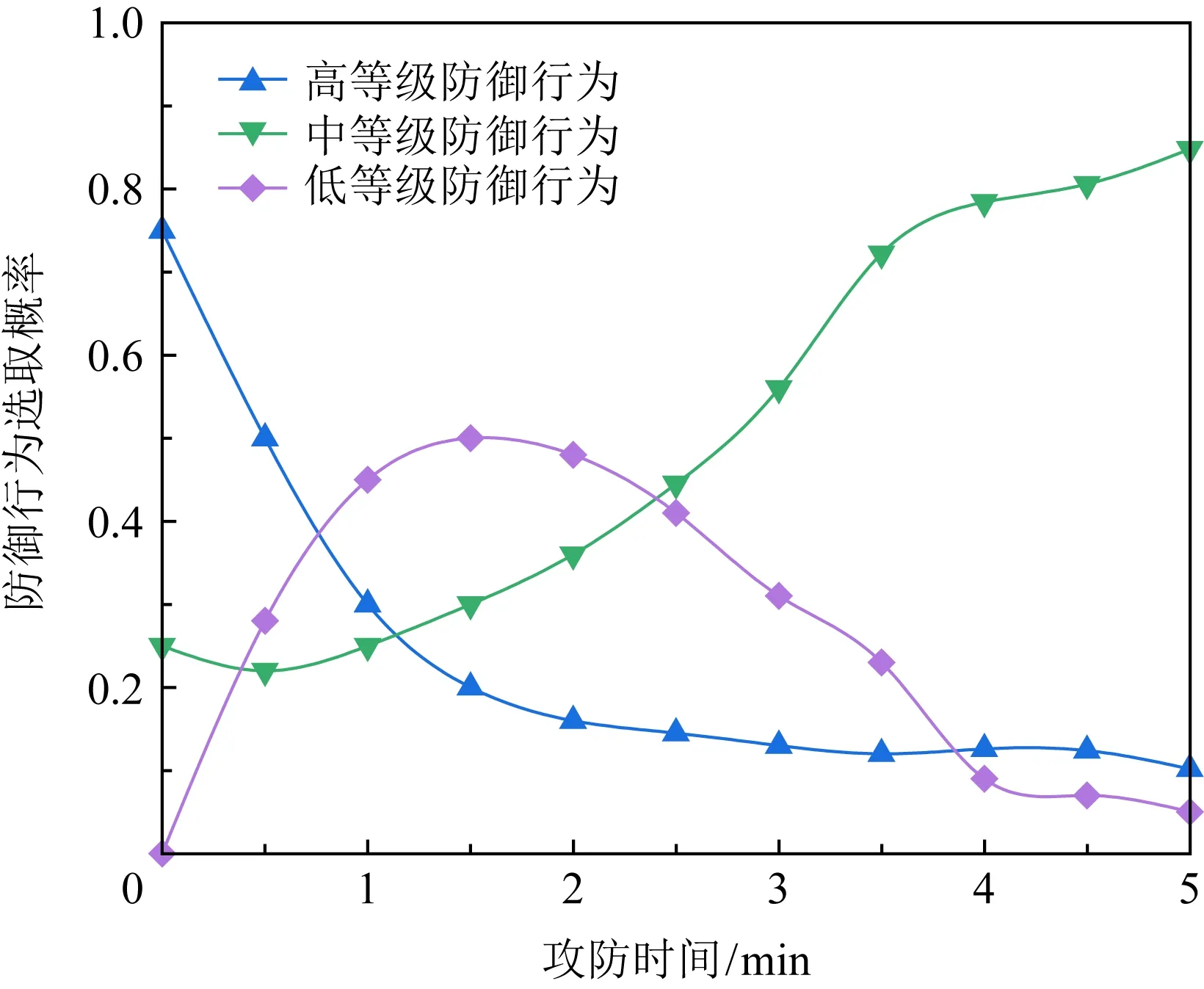
Fig. 5 Optimal policy control trajectory of defense图5 防御策略的最优控制轨迹

对于攻击者，当τ∈[0,0.25)时，选择攻击行为AH；当τ∈[0.25,5]时，选择攻击行为AL.对于防御者，当τ∈[0,0.78)时，选择防御行为DH;当τ∈[0.78,2.45)时，选择防御行为DL；当τ∈[2.45,5]时，选择防御行为DM.

由于实验中攻击行为分为高低等级2种类型，其策略概率之和为1，故仅将高等级攻击策略概率与3种不同等级防御策略结合以分析实验结果.

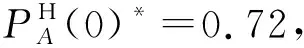
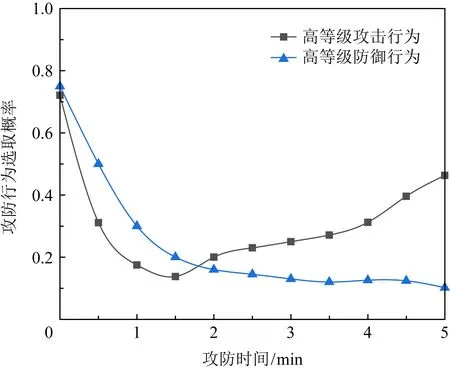
Fig. 6 Optimal policy control trajectory of strategy图6 策略和最优控制轨迹

Fig. 7 Optimal policy control trajectory of strategy图7 策略和最优控制轨迹

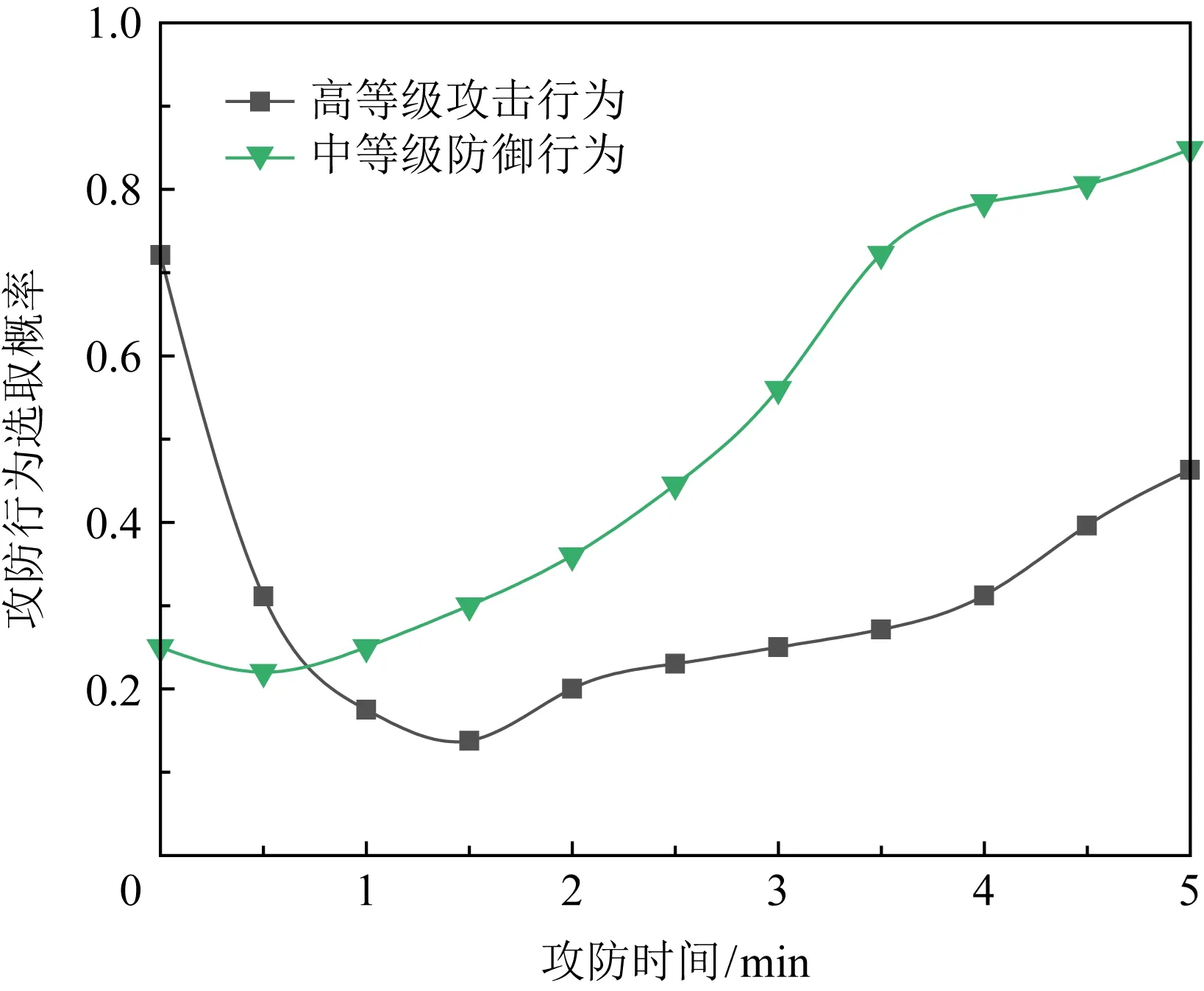
Fig. 8 Optimal policy control trajectory of strategy图8 策略和最优控制轨迹

3) 如图9所示，当τ∈[0,0.25)时，攻击者发起突袭式高等级攻击行为AH进攻数据库服务器，导致数据库服务器的安全状态快速下降，此时防御者及时做出反应，采取高等级防御行为DH,所以数据库服务器安全状态曲线虽在下降，但下降速率逐渐降低，直到τ=0.2时成功阻止攻击者对数据库服务器的进一步损害，并随后逐步提高数据库服务器的安全状态.

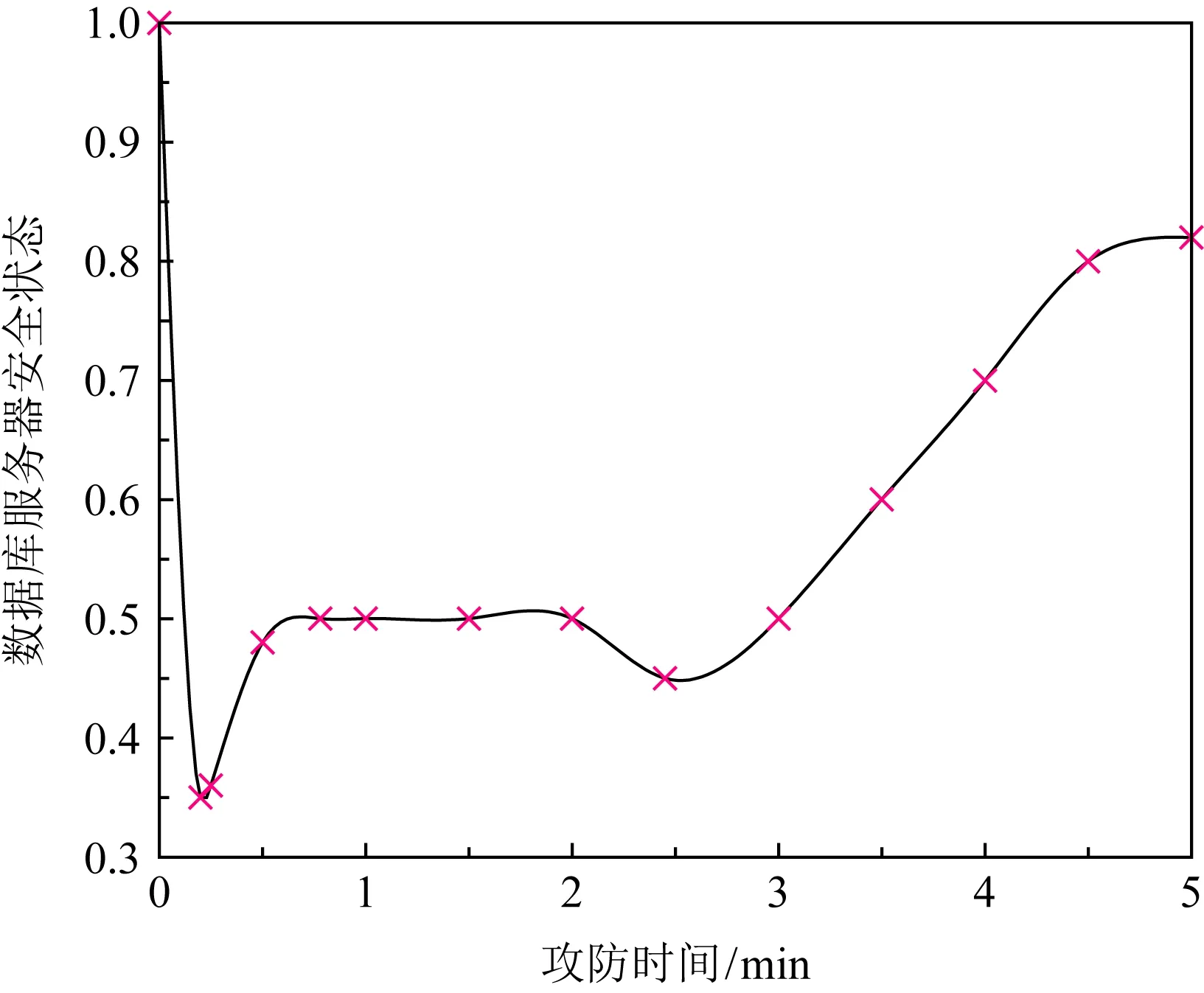
Fig. 9 The evolution trajectory of database serversecurity state S(τ)*图9 数据库服务器安全状态S(τ)*演化过程轨迹

当τ∈[0.2,0.25)时，攻击者发现无法进一步窃取数据库服务器的信息后，考虑自身攻击付出巨大代价，开始选取攻击行为AL.当τ∈[0.25,0.78)时，防御者为快速提高数据库服务器的安全状态，在攻击者选择AL的情况下，依然选择DH，以防止出现攻击者再次选择高等级攻击而无法防御的情况，此时主机安全状态快速上升.当τ=0.78时，防御者选择DL，数据库服务器安全状态的上升速率逐渐变慢，在与AL相互作用下，服务器安全状态维持在0.5水平.

4.3 模型对比

与文献[3]的时间离散模型攻击策略控制过程进行对比，结果如图10所示.设文献[3]中每个阶段持续时间为1 min.

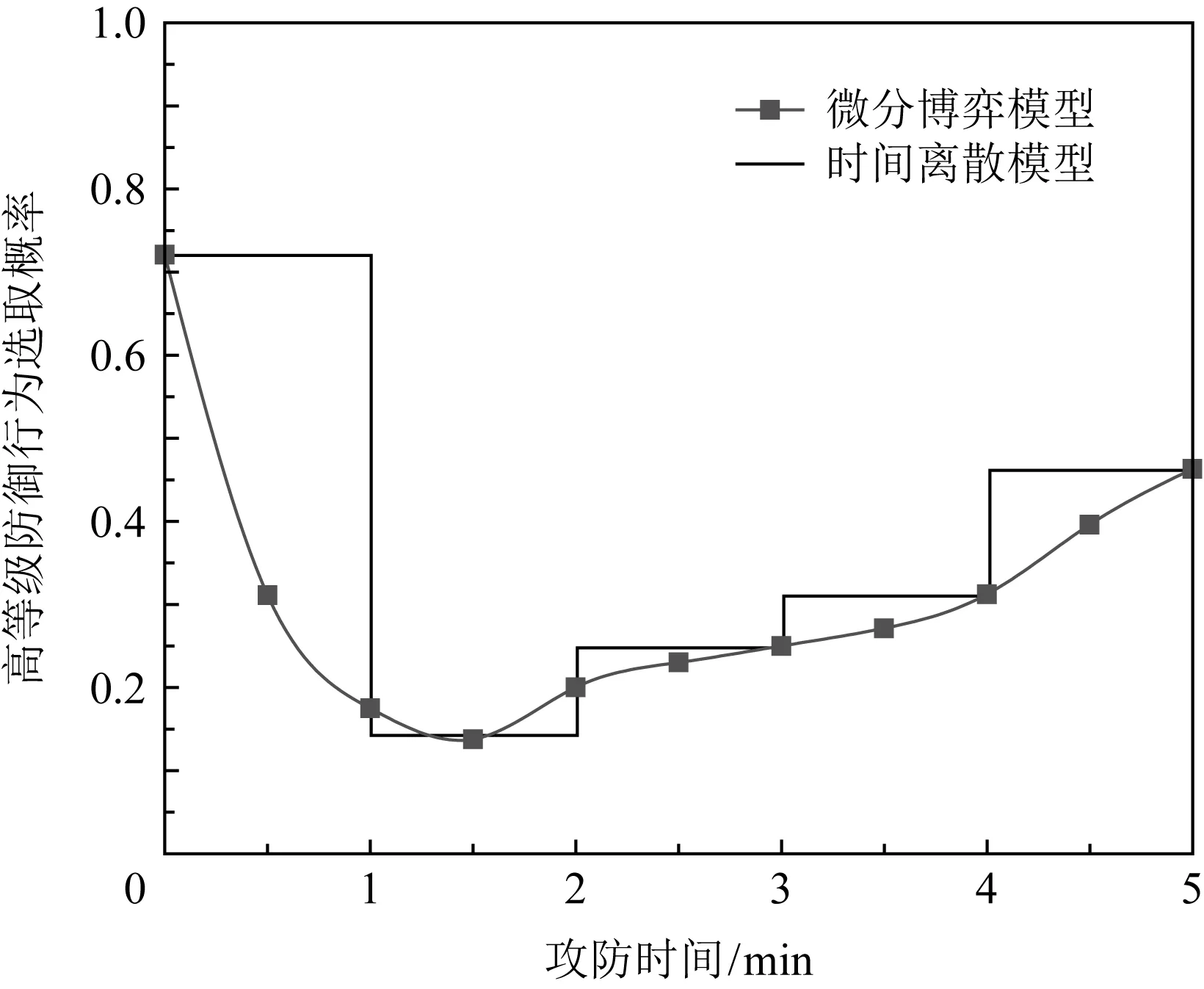
Fig. 10 Optimal strategy control trajectory of high-level attack图10 高等级攻击最优策略控制轨迹

当攻击者采取文献[3]的时间离散算法发动网络攻击时，仅在各阶段开始时选取新策略，攻击策略变化不灵活，导致攻击者的目标收益效用降低.由定理1可知，理性攻防博弈的关键在于防御者会针对最优攻击策略采取最优防御策略.攻击效用降低将使得防御者“轻视”攻击者，进而采取非最优策略.

当攻击者采取本文微分博弈算法进行网络攻击时，若防御者利用文献[3]时间离散模型选取防御策略，其阶段式变化的防御策略将永远滞后于攻击者的实时攻击，进而导致网络空间受到威胁.

综上分析，给出5个防御建议：1)防御者应加强平时防御水平，避免攻击者的突袭式攻击造成网络无法挽回的损失；2)对于网络系统重要节点，应该强化相关检测程序，避免与被劫持主机保持通信；3)应对低等级攻击时，防御者不应放弃静态防御策略，在保证网络安全的前提下尽可能降低网络开销；4)相较于静态防御而言，防御者平时应多考虑使用MTD策略，这样的收益代价比更大，防御范围更广，防御效果更好；5)使用与时间相关的防御策略选取方法，例如本文方法，以提高防御行为决策的灵活性，使受保护网络在攻防对抗中能够长时间处于安全状态.

5 总 结

本文对时间连续的网络攻防过程以及MTD最优策略进行综合研究，构建移动目标防御微分博弈模型MTDDG.在此基础上，考虑到网络内部微观节点行为与宏观传播现象之间的相互依赖会对网络攻防决策产生影响，按照实际情况设定网络内部主机的开关机和通信状态，对网络内部重要节点建立安全状态演化方程，提出MTDDG的求解方法和最优MTD策略选取算法.仿真实验验证本文提出模型和方法的有效性.基于实验成果对网络系统重要节点防御提出关键建议，为连续、实时网络攻防对抗中MTD策略做出指导.

未来工作主要是改进网络攻防微分博弈的求解算法，利用反馈纳什均衡求解微分博弈方程，进一步从时间相关性方面提升MTD防御效果.