基于激光多普勒的杯形波动陀螺频率裂解测量

李靖轩，孙小燕，于亚龙，林 星，胡友旺

(1.高性能复杂制造国家重点实验室，湖南长沙 410083；2.中南大学机电工程学院，湖南长沙 410083)

0 引言

杯形波动陀螺是固体波动陀螺的一种，利用谐振子的振动产生驻波，进而敏感转动角度产生哥氏效应，实现角速度的测量[1-2]。与传统的机械转子陀螺相比，杯形波动陀螺的结构更为简单，具有精度高、稳定性好、使用寿命长等优点。

由于杯形波动陀螺的振动幅度较小，且附加质量会对陀螺的振动特性产生影响，因此频率的测量应尽量采用非接触式的方法。激光多普勒测振仪作为一种典型的非接触式测量仪器，具有频率响应范围大、动态范围宽、高精度、高分辨率等特点，被广泛应用于微器件的振动测量[3-4]。

本文设计了扫频激励、单频激励2种激励方案，在周向不同方位对陀螺进行激振，利用激光多普勒测振仪进行振动信号的采集，实现了陀螺频率裂解的准确测量，并对陀螺的低频轴与高频轴进行了区分，为陀螺的调谐与性能表征提供了支持。

1 测试原理

1.1 陀螺基本工作原理

杯形波动陀螺有驱动模态与检测模态2个工作模态，如图1所示，两者在周向相隔45°。陀螺利用哥氏效应实现角速度的测量，当激励位于驱动模态方位、激励的频率与谐振子的固有频率相同时，驱动模态的驻波被激励出来，谐振子做四波腹运动；当有轴向角速度输入时，陀螺谐振子上振动各点受到哥氏力作用，检测模态被激励出来[5-7]。

图1 杯形波动陀螺工作模态

将陀螺谐振子视为只在自身平面内振动的薄弹性环，建立谐振子的环形模型。克里莫夫等人证明，受外分布载荷作用时，圆环的运动微分方程可以表示为如下形式[8]：

(1)

假设作用于谐振子的激励力为F=Asinωt，由于谐振子沿切向变形很小，可近似认为pv=0，则可得到pw的表达式为[9]

pw=f(φ)Asinωt

(2)

式中

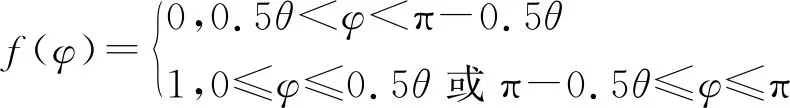
式中θ表示激励作用范围。

将f(φ)在[0,π]范围内进行傅里叶展开，由于仅分析谐振子在工作模态下的振动，因此只保留圆周角的二次谐波，得到激励法向分量表达式为

(3)

代入式(1)，则圆环的运动微分方程为

(4)

该方程的解可以表示为以下形式：

w(φ,t)=p(t)cos2φ+q(t)sin2φ

(5)

将式(5)代入式(4)，使用布勃诺夫-加廖尔金法，可以求得谐振子在外部激励作用下的边缘位移为

w(φ,t)=k2sinωtcos2φ+k4sinωtsin2φ

(6)

当没有角速度输入时，谐振子边缘位移只有k2项，只在驱动模态振动；当有角速度输入时，谐振子的运动则是工作模态与检测模态振动的合成。

理想情况下，两工作模态的谐振频率是一致的。但受谐振子材料不均匀性、加工误差等因素影响，谐振子工作时驱动模态与检测模态的固有频率间存在差值，称之为频率裂解[10-11]。此时由于质量偏差四次谐波的存在，理想谐振子中的驻波被破坏而发生进动，谐振子的振动过程可以表示为2个谐波振动和的形式[12]：

w(Φ,T)=Acos2φcos2φ0cosω1t+Asin2φsin2φ0cosω2t

(7)

式中：A是谐振子的振动幅值；φ0是波相对于低频轴的方位；ω1、ω2分别是两工作模态的振动频率。

当激励不位于驱动模态或敏感模态所在方位，而是处于两工作模态之间时，陀螺的振动是两工作模态振动的叠加，同时包含2个模态的振动信息，通过采集此时的振动信号并进行频谱分析，即可实现频率裂解的测量。

1.2 激光多普勒测振原理

激光多普勒测振仪利用光的多普勒效应测量物体表面的位移和速度[13-14]，其工作原理如图2所示。激光源发出的激光束，由分光镜分解为同频率同相位的测量光束和参考光束；测量光束通过透镜聚焦在被测物体的振动表面，光波的频率发生变化，经振动表面反射至光敏元件处；通过计算测量光束与参考光束的频差，即可求得被测件的振动速度：

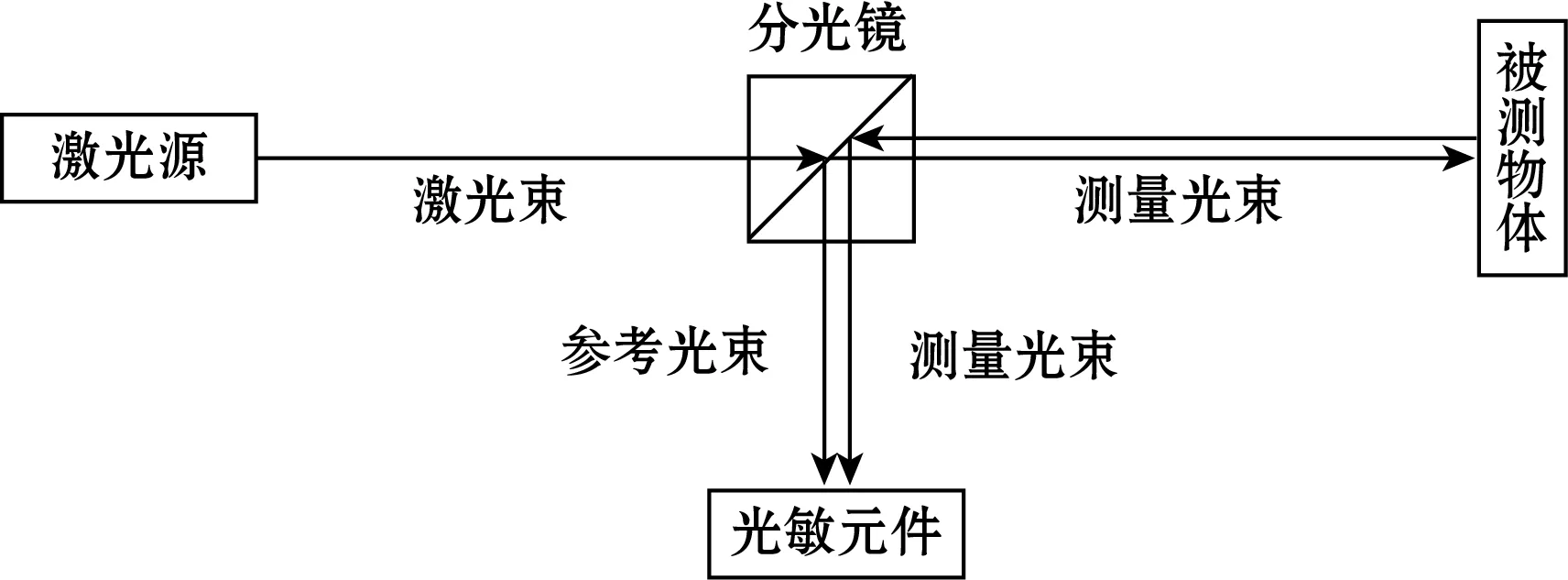
图2 激光多普勒测振原理

(8)

式中:Δf为测量光束与参考光束的频差;v为被测结构振动速度；λ为激光波长。

2 测量方案设计

2.1 激励方式与激励信号的选取

只有当激励位于两工作模态之间时，采集的振动信号中才同时包含2个模态的振动信息。杯形波动陀螺通常采用压电驱动的方式，且压电片的粘贴位置与两工作模态所在方位一致，无法实现2个工作模态的同时激振，因此必须选择其他的激励方式。

常见的非接触式激励方式主要有声激励、静电激励和磁激励。由于声激励装置简单易于实现，且当激励源与陀螺距离较近时，可以认为激励源产生的声波具有较好的指向性，因此本文选择麦克风作为陀螺的激励源。为保证陀螺被充分激振，所选用的麦克风应具有充分的输出功率，这使得麦克风尺寸较大，因此在麦克风前设置了一中心开有圆孔的挡板，以保证声波准确的激励目标位置。

常用的激励信号有正弦激励、冲击激励和随机激励，其中，冲击激励和随机激励一般用于激励出被测件的所有振动模态[15]。由于只关心陀螺两工作模态的谐振频率，无需激发其他模态，且正弦信号易于控制，因此选择正弦信号作为陀螺的激励信号。

2.2 实验装置

激光多普勒振动测试系统如图3所示，主要由信号发生器、麦克风、激光多普勒测振仪、计算机组成。信号发生器产生频率和幅值一定的激励信号，施加到麦克风的两驱动端，使麦克风产生高频振动。麦克风在振动过程中对周围的空气产生周期性压力，传导至陀螺谐振子的目标激励位置，实现谐振子的驱动。谐振子的振动信号由激光多普勒测振仪采集，并传送至计算机进行分析处理，实现陀螺频率的测量。

(a)原理示意图

(b)实验装置图图3 激光多普勒振动测试系统

3 实验与讨论

测量陀螺的频率裂解时，根据激励源与陀螺的相对位置，既可以同时激励2个工作模态，同时测量两模态的谐振频率，也可以单独激励2个工作模态，分别测量两模态的谐振频率。针对上述两种情况，本文采用扫频信号、单频信号两种激励信号，分别开展实验。

3.1 同时激励两工作模态

扫频激励是用频率缓慢变化的正弦信号对结构进行激励，当频率变化率小时，可以认为实际的测量数据具有稳态响应的特征；当响应出现最大幅值时，即表明是该振动模态的固有频率。测量时，首先在大频率范围内进行粗扫频，确定陀螺的大致谐振频率；然后在谐振频率附近进行细扫频，实现频率裂解的测量，细扫频时主要参数设置如表1所示。

表1 扫频主要参数值设置

扫频激励所测得的时域信号及对应频域信号如图4所示。随着激励信号频率的增长，陀螺谐振子的振动速度不断增大，并出现第一个峰值，该峰所对应的频率即为一个模态的谐振频率；随着激励信号频率继续增大，由于逐渐远离第一个模态的谐振频率，导致振动速度减小；当激励频率靠近第二个模态谐振点时，振动速度再次增大，直至到达谐振点而出现第二个峰值。

(a)时域图

(b)频域图图4 扫频激励双模态

单频激励信号的频率固定、幅值不变，具有激励功率大、信噪比高、信号稳定的特点。测量时，设置单频信号的频率为5 100 Hz，略高于陀螺的谐振频率；当陀螺受激振动一段时间后，撤除激励信号，使陀螺作衰减振动，并由激光多普勒检测该过程的振动信号。在衰减过程中，陀螺的振动频率会经过两工作模态固有频率而发生谐振，振幅显著增加，通过对信号进行FFT变换，即可实现频率裂解的测量。

单频激励所测得的时域信号及对应频域信号如图5所示。初始时段，由于陀螺振动频率远离两模态谐振频率，所以振动很微弱；随着衰减振动的进行，出现了2个振动速度显著增加的峰值，这2个峰所对应振动频率即为2个模态的谐振频率。由于衰减过程中能量损耗较快，导致时域第二个峰值明显小于第一个峰值。

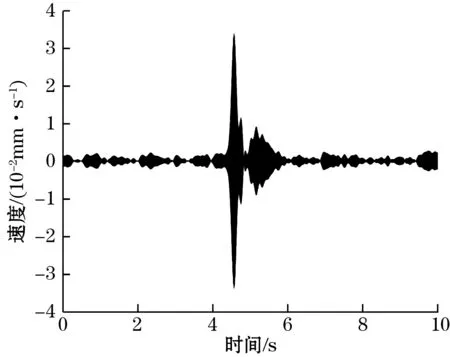
(a)时域图

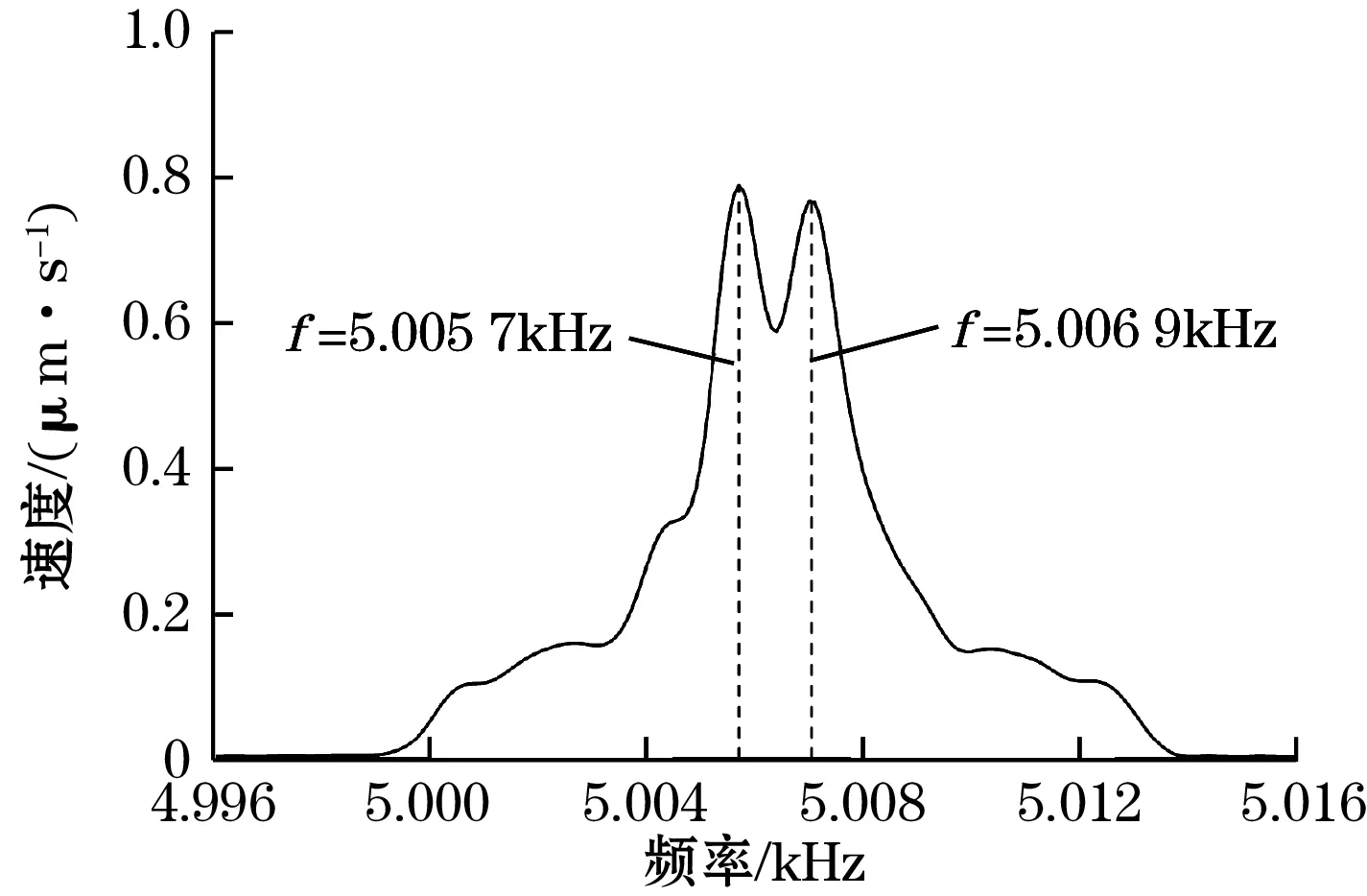
(b)频域图图5 单频激励双模态

采用上述两种激励信号进行多次测量，所得数据如表2所示

表2 同时激励两模态频率测量值 Hz

为衡量两种激励方案的测量稳定性，引入标准差作为评判依据。扫频激励方式下，A、B模态频率测量值的均值分别为5 005.742 Hz和5 006.935 Hz，标准差分别为0.026 7Hz和0.020 6 Hz；单频激励方式下，A、B模态频率测量值的均值分别为5 005.717 Hz和5 006.983 Hz，标准差分别为0.068 7 Hz和0.146 2 Hz。单频激励较扫频激励的标准差更大，主要是由于陀螺在空气中振动衰减很快，导致采样时长较短，而FFT变换的分辨率与采样时长成反比，使得分辨率较低，可通过真空环境测量的方式加以改善。

扫频激励、单频激励所测频率均值基本一致，频率裂解分别为1.193 Hz，1.266 Hz，两者的测量结果具有较好的一致性。

3.2 分别激励两工作模态

将麦克风分别对准陀螺的2个工作模态，采用扫频信号、单频信号分别进行激励，所测得的数据如图6、图7所示，此时，陀螺的振动中只包含某一模态的振动信息，因此时域图中的振动速度只出现单个峰值。

采用2种激励信号进行多次测量，所得数据如表3所示。

表3 分别激励两模态频率测量值 Hz

扫频激励下，A、B模态频率测量值的均值分别为5 005.877 Hz、5 006.957 Hz，标准差分别为0.017 0 Hz、0.026 2 Hz；单频激励下，A、B模态频率测量值的均值分别为5 005.950 Hz、5 007.067 Hz，标准差分别为0.050 0 Hz、0.047 1 Hz。2种激励方案仍具有较好的测量稳定性。扫频激励、单频激励所测频率均值基本一致，频率裂解分别为1.080 Hz、1.117 Hz，频率裂解的测量结果仍具有较好的一致性。

在上述2组实验中，单频激励方案由于采样时间短，频率分辨率较低，因此测量稳定性较扫频激励略差，但能够实现谐振频率与频率裂解的快速定位；扫频激励方案频率分辨率较高，测量稳定性较好，但前期一般需多次粗扫频以确定细扫频的参数配置，且单次测量耗时较长。可以将两种激励方案相结合，先通过单频激励，实现谐振频率与频率裂解的快速确定；再通过扫频激励，实现谐振频率与频率裂解的准确测量，从而在保证测量准确性的同时，使测量效率得到提高。

(a)A模态时域图

(b)A模态频域图

(c)B模态时域图

(d)B模态频域图图6 扫频激励单模态

(a)A模态时域图

(b)A模态频域图

(c)B模态时域图

(d)B模态频域图图7 单频激励单模态

3.3 低频轴与高频轴的区分

在采用去除质量式方法对陀螺进行调谐时，需要在陀螺谐振子的低频轴位置进行材料去除，使低频轴的固有频率增大。因此需要对低频轴与高频轴进行区分，以便在调谐前明确修调位置；在调谐后判断是否发生高低频轴的交换，避免过修调现象的发生。

低频轴与高频轴的区分可以在3.1节扫频方式测量频率裂解完成后进行。将谐振子转动一定角度，则激励会靠近某一工作模态并远离另一模态，根据式(7)，靠近的模态时域幅值会增大，远离的模态时域幅值会减小。由于扫频方式为低频率向高频率步进，因此，第一个峰对应低频轴，第二个峰对应高频轴；设第一个峰与第二个峰的幅值之比为β，当β<1时，说明激励在靠近高频轴；当β>1时，说明激励在靠近低频轴。按照表1的扫频参数对谐振子进行激励，同时利用激光多普勒测振仪记录谐振子的时域振动信号，所得波形如图8所示。

(a)顺时针转动谐振子

(b)逆时针转动谐振子图8 低频轴与高频轴的区分

当陀螺谐振子沿顺时针方向转动一定角度时，得到图8(a)所示波形。此时β<1，说明激励在远离低频轴而靠近高频轴，所以低频轴在激励的顺时针方向。也可以将陀螺谐振子沿逆时针方向转动一定角度，测量结果如图8(b)所示。此时β>1，说明激励在靠近低频轴而远离高频轴，所以低频轴在激励的顺时针方向。谐振子转动方向的不同对低频轴与高频轴的判断结果没有影响。

4 结束语

针对杯形波动陀螺的频率裂解测量问题，本文设计了扫频激励、单频激励两种激励方案，在周向不同位置实现陀螺的激振，并利用激光多普勒测振仪实现振动信号的采集。测量结果表明，在同时激励两工作模态或分别激励两工作模态情况下，两种激励方案均能够实现陀螺谐振频率与频率裂解的稳定测量，且测量结果具有较好的一致性；在此基础上，还对陀螺的低频轴与高频轴进行了区分，为陀螺的调谐与性能表征提供了保障。