横向弯曲效应对大跨度人行悬索桥短吊索影响的分析

2021-08-16徐自然朱朝银

公路工程 2021年3期

徐自然,张欣,朱朝银

(1.湖南省交通规划勘察设计院有限公司，湖南长沙 410200；2.中南大学土木工程学院，湖南长沙 410075)

0 引言

人行悬索桥兼顾造型优美和跨越能力大的特点，已被广泛应用到景区桥梁建设中。目前国内外已建成多座大跨度人行悬索桥，均引起了强烈的社会反响，如日本九重梦人行悬索桥(全长390 m)、临沂蒙山人行悬索桥(主跨420 m)[1]、张家界大峡谷人行桥(全长430 m)[2]等。与公路悬索桥相比，人行悬索桥桥面更窄、主梁更柔、刚度相对更小，活载(尤其是横桥向风荷载)作用下的变形效应更为显著，构件受力变化对外界因素更为敏感。

活载作用下，大跨度人行悬索桥在纵、横向的变形均较大。广泛应用的平行钢丝吊索常通过销铰与索夹连接，这种连接方式可适应纵向变形，但不能适应横向大位移变形。尤其对于跨中短吊索而言，上下端横向变位不协调会导致钢丝吊索局部弯曲，引起较大的附加应力，需要重点关注。然而，目前国内外对人行悬索桥短吊索横向弯曲效应的研究较少，在对短吊索选用上通常以经验为主。如张家界玻璃人行桥跨中区域布置27对带有双向转动销铰的刚性吊杆(其余均为钢丝吊索)[3]以减小吊索弯曲效应。但并未就该类刚性吊杆的设置原则做出详细说明。因此，为更有效地指导大跨度人行悬索桥吊索的选型，有必要从理论上分析吊索横向弯曲效应的影响程度，明确横向大变形条件下高强钢丝吊索的适用范围。

本文从缆索的弯曲理论出发，推导了吊索横向弯曲应力计算公式，并以某景区大跨度人行悬索桥为工程背景，分析了弯曲效应对吊索应力的影响，优化了本工程项目吊索形式并给出了相关建议，可为类似人行悬索桥设计提供参考。

1 吊索横向弯曲应力分析

大跨度人行悬索桥在横向风荷载作用下会发生较大的横向变形，连接吊索的主缆端和主梁端水平位移的不一致必然会使钢丝吊索弯曲变形。对于上下端位移差大、长度短的吊索，其弯曲效应尤为明显，需重点关注。为分析弯曲效应对吊索受力的影响，须模拟吊索弯曲形态、推导弯曲应力计算公式。

1.1 假设条件

为简化分析，根据吊索及连接组件的构造，提出以下假设条件：

a.在横桥向变形中，吊索连接组件(如锚头、耳板、索夹)刚度远大于钢丝吊索，故假定上下锚杯之间吊索两端为固结形式，且锚杯无横向转角。

b.吊索索体弯曲刚度均匀，反弯点位于吊索有效弯曲范围的1/2高度处。

根据假设条件，吊索横向弯曲状态见图1。

图1 吊索横向弯曲示意图

1.2 弯曲应力分析

借鉴WYATT公式[4]，结合吊索弯曲状态及建立的坐标系，吊索任意截面可得：

(1)

(2)

其中,y0=hsinθ-Δcosθ。

根据边界条件可求得常量A、B分别为：

(3)

显然吊索端部处弯矩最大，其局部弯曲应力为：

(4)

式(1)～式(4)中:T为吊索轴力；EJ为吊索弯曲刚度;A、B为常量;σs为轴力T对应的吊索应力。

由式(4)可以看出吊索弯曲刚度(半径)的取值仅影响θ值计算，因此在计算g时，取等效整截面刚度(按等效直径计算)，结果偏安全。

2 工程背景

某景区大跨度人行悬索桥为双塔单跨简支地锚式悬索桥。桥型布置为16 m简支梁+338 m双塔单跨悬索桥+16 m简支梁。主缆为平行索面，矢跨比为1/12，横向间距为7.1 m，单根主缆由37股通长索股组成，每根预制索股包含61丝、直径5.0 mm的镀锌高强钢丝。为增加结构稳定性，拟在主梁下方设置空间抗风缆系统，抗风缆所在理论平面与水平面成45°夹角，全桥总体布置如图2所示。

图2 桥型总体布置图(单位：cm)

索塔为曲线形框架式混凝土结构。加劲梁为钢-混组合梁结构，由分离式双边箱梁、中央小纵梁、横梁的梁格体系以及混凝土桥面板组合而成，其中钢结构高0.8 m，混凝土板厚0.18 m，加劲梁结构宽7.1 m(不含封嘴)。

吊索拟采用高强平行钢丝，纵向间距6 m，单根吊索由32根φ5.0 mm镀锌高强钢丝组成，吊索上端通过叉形耳板与索夹连接，下端通过叉形耳板与加劲梁吊点耳板连接，吊索连接如图3所示。

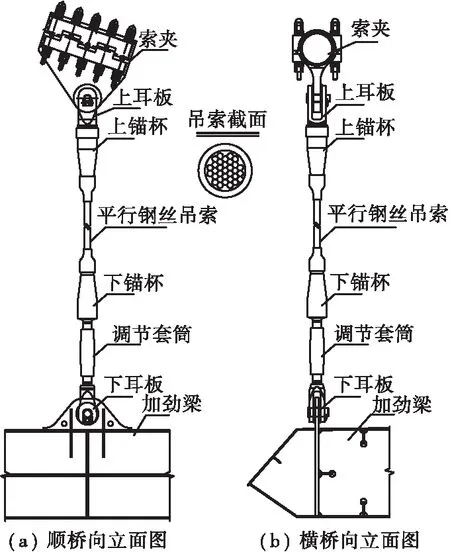
图3 吊索连接图

3 实例分析

以前文所述的大跨度人行悬索桥为工程背景，根据吊索横向弯曲应力计算公式，分析横向弯曲对吊索的附加效应。

3.1 计算模型

为分析抗风缆对水平位移约束的效应、对比抗风缆刚度对水平位移的影响，建立了3种结构模型进行比较。

a.基本结构，模型中不设抗空间风缆。

b.抗风缆结构，设置空间抗风缆系统，抗风缆张拉取为2.5 MN。

c.加强型抗风缆结构，设置空间抗风缆系统，抗风缆张力取为5.2 MN。

采用西南交通大学的桥梁结构非线性分析系统BLNAS软件建立全桥空间有限元模型。桥塔、主梁采用梁单元模拟，主缆、吊索、抗风缆、抗风拉索均采用杆单元模拟。为保证吊索弯曲长度，采用刚臂模拟吊索上下端连接组件。运营阶段横向荷载仅考虑横桥向风荷载，桥位处百年一遇基本风速取27.2 m/s,按《公路桥梁抗风设计规范》(JTG/T 3360-01-2018)计算各构件风荷载。

3.2 吊索水平位移分析

通过有限元模型计算上述3种结构在横向风荷载作用下的水平位移，得到吊索上下端横桥向水平位移差(下文简称位移差)，结果汇总如图4所示。由计算结果可知，设置抗风缆可有效减小横向荷载作用下吊索位移差，跨中区域吊索位移差减小幅度约40%；不同抗风缆刚度(不同张力)对吊索位移差的影响较小，影响幅度仅在5%以内。因此，对于大跨度人行悬索桥，空间抗风缆系统可有效减小结构横向变形，但抗风缆张力只需合理选取、不必盲目增大。

图4 吊索上下端位移差

3.3 吊索弯曲应力分析

由式(4)可知，在材料及拉索应力确定的条件下，弯曲应力仅与转角θ有关，因此θ计算的准确性至关重要。本文以抗风缆结构模型为对象，选取跨径1/8处、1/4处、3/4处、1/2处吊索，对比分析精确计算法和简化计算法对弯曲转角精度的影响，计算结果汇总如表1所示。结果表明，简化计算值略小于精确计算值；越靠近跨中，其影响越大；本模型跨中吊索转角影响幅度达9.3%。因此，建议在初步设计中可近似按简化法计算，但在施工图设计中宜采用精确计算值。

有限元模型计算表明，横向风荷载引桥的吊索内力很小，不足恒载效应的0.5%，故本文取σs为吊索恒载应力。根据前文推导的弯曲应力计算公式，计算3种结构模型中吊索弯曲应力，结果汇总如图5所示。结果表明，吊索横向弯曲应力明显，越靠近跨中，其效应越为显著；在基本结构模型中，跨中短吊索横向弯曲应力约为恒载应力的1.85倍；其余2种结构模型中，跨中短吊索弯曲应力仍达到恒载的1.14倍，远大于活载效应。因此，该类结构纤细、刚度小的大跨度人行悬索桥在设计吊索时应重点关注短吊索横向弯曲效应。

表1 弯曲转角计算精度分析Table1 Accuracyanalysisofbendinganglecalculation计算方法θ=Δh+Δ-1/gθ=Δh(简化法)影响幅度/%1/8L0.00250.00241.51/4L0.00730.00722.43/8L0.01600.01525.11/2L0.02520.02309.3

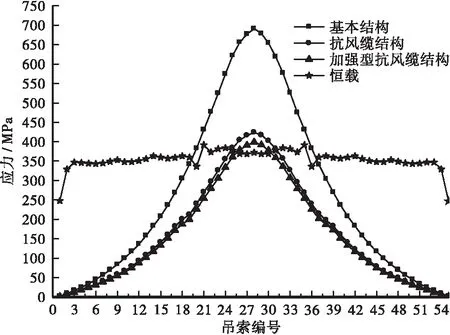
图5 横向风荷载下吊索弯曲应力

3.4 吊索组合应力分析

在本项目工程设计中，人行悬索桥恒载作用下的吊索应力水平较低，均小于400 MPa；而以人群荷载为主的活载产生的效应仅约恒载效应22%。景区为了保证游客安全，当桥面风速大于15 m/s时，将禁止游客通行；桥位处设计基准风速为27.2 m/s(离水面10 m高度处)。因此，恒载+横向极限风荷载为吊索考虑横向弯曲效应的最不利工况，本文以此工况下的组合效应作为吊索设计依据。

本工程中吊索采用1 770 MPa高强镀锌钢丝，根据《公路悬索桥设计规范》(JTG/T D65-05-2015),吊索在承载能力基本组合作用下的限值为804 MPa。3种结构模型吊索组合应力结果汇总如图6所示。结果表明，在考虑吊索横向弯曲效应下，基本结构模型中16#～40#吊索组合应力均超过规范限值，跨中短吊索最大超出幅度达95%；设有抗风缆系统的两个结构模型中，20#～36#吊索组合应力也均超过限值，最大超出幅度达40%。因此，对于大跨度人行悬索桥的设计，除布置空间抗风缆减小横向变形外，尚需进一步采取适当的措施减小吊索弯曲效应、降低吊索组合应力。

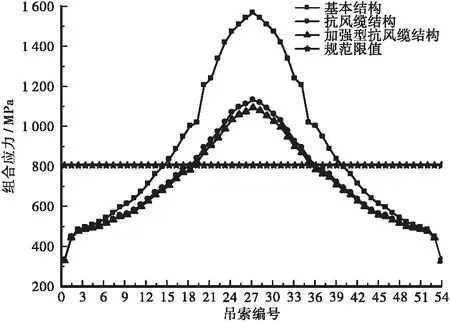
图6 吊索组合应力

3.5 措施及建议

虽然本工程中采用了抗风缆来减小横向变位，但20#～36#吊索在考虑横向弯曲效应下，其组合应力仍超过规范限值，而恒载应力水平尚小于400 MPa，若通过增大吊索截面尺寸来减小应力，显然既不经济又不合理。因此，减小横向弯曲应力是该类吊索设计的关键，增设横向转动销铰可降低横向转动约束、减小横向弯曲效应。本工程中，跨中吊索总成长仅2.7 m(吊索上耳板销孔中心至下耳板销孔中心)，钢丝吊索上下端组件总长为2.4 m(含上下耳板、上下锚杯、调节套筒等构件)，钢丝吊索已不能满足横向转动销铰的布置。为减小吊索连接构件长度、满足纵横双向转动销铰的布置，本工程对需设双向销铰的吊索均采用钢拉杆形式，20#～36#钢拉杆吊索构造如图7所示。

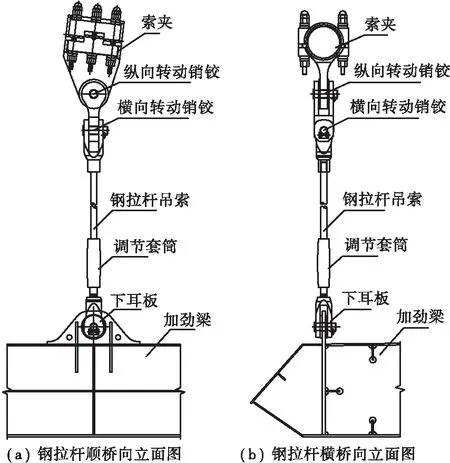
图7 双向销铰钢拉杆

以本工程为参考，可将吊索弯曲分析推广至同类人行悬索桥项目。假定吊索采用1 770 MPa高强钢丝，恒载作用下吊索应力为400 MPa，以恒载应力+横向弯曲应力组合值作为设计依据。为满足规范限值，横向弯曲应力σs不应大于180 MPa，采用θ简化计算公式，进一步可估算得Δ/h≈0.01，即若吊索上下端位移差大于吊索长度的0.01倍时，考虑弯曲效应的应力组合可能会超过规范限值，此时宜进行精细分析，必要时应设横向转动销铰、释放弯曲应力。