多点激励中的控制载荷存在性
2021-08-16胡杰
胡杰
(1.中国工程物理研究院 总体工程研究所,四川 绵阳 621999;2.工程材料与结构冲击振动四川省重点实验室,四川 绵阳 621999)
装备结构在定型并投入到实际工程应用之前,往往都需要通过环境试验对其环境适应性进行考核,其目的是在试验室中通过模拟实际环境的载荷工况或者使得产品产生与其在实际工况下等效的响应,以考察装备结构是否能够满足各项指标要求。其中,振动环境对大多数装备结构而言,都是在实际使用过程中不可避免的载荷工况,因此在环境试验中扮演着重要的角色。
振动环境试验中,最常采用的加载设备为振动台,试验中一般是在台面或者产品上设置响应控制点,使得控制点产生预期的响应。目前最常见的形式为单点激励方式,即采用单个振动台加载。这种试验方式应用比较成熟[1],诸多试验规范和标准也制定了相关的规定[2]。但该试验方式只能对单个测点的响应进行控制,产品上其他部位的响应往往不受控,即只能保证单个测点的响应达到预期目的。当前试验中常采用的多点平均响应控制方式实质上仍属于单点控制,只不过是对某个虚拟点的控制而已,多个点的平均响应满足控制要求,但各个测点之间差异往往很大。
从上述分析来看,如果振动环境试验中能够在多个点上实现响应控制,那么产品的响应将能更真实地与其在实际使用环境下等效[3-5],尤其是针对尺寸较长的结构[6]。此时就需要借助多点激励方式,即搭建多个加载设备(如多个振动台)构成的激励系统。刘志华等[7]针对正弦激励情况,提出了多点激励正弦振动实数域控制算法的控制流程。对于振动环境中最为关注的随机振动工况,20世纪80年代由Small-wood等[8-9]初步建立了多点随机振动控制方法,建议根据重要性程度,对谱矩阵中的对角线元素进行排列,靠前的元素优先收敛,但无法实现多点加权综合控制。刘青林等[10]采用柔性悬挂-多点激励试验方法对某弹体结构飞行过程中的面载荷进行了有效模拟。谢志勇等[11]研究了结构在力型输入和加速度型输入条件下,多点激励的振动响应求解方法,结果表明,采用力型输入与实验吻合最好。韩伟等[12]应用虚拟试验技术在试验前进行试验方案设计及优化,验证了双点激励虚拟试验的准确和可靠性。李永华等[13]则在数值模拟方法上,对多点激励下的响应求解开展了研究,提出了多点激励下绝对位移直接求解的虚拟激励法,并进一步对该算法开展了误差的频域分析[14]。
多点激励的难点主要是多点激励之间相关性(体现为互谱)的控制,体现了多个激励载荷之间的协调配合。贺旭东等[15-16]从试验控制的角度对互谱矩阵开展了仿真研究,基于矩阵分解提出了获得试验驱动信号的控制算法,但对于互谱元素非零的情况还有待进一步深入研究。叶建华[17]开发了双振动台随机振动试验控制系统样机,对2个控制点的不同响应功率谱密度分别进行了控制。祝济之等[18]将2个响应控制点设置在夹具与试验件的连接处,较好地将2个振动台的激励传递到试验件上。
从上述分析来看,在目前多点激励的研究中,一般考虑的是激励数量与响应控制点数量相同的情况,控制的响应点越多,等效程度越高,试验效果越好,但要求的加载设备也越多。实际情况下,搭建由多个加载设备构成的协调激励系统往往较为困难。如四点响应控制中,搭建4个振动台的激励系统并非易事,且协调加载要求也很高,难度也更大。此时,若能够通过少量的加载设备实现多点响应控制将具有重要的实际应用意义。其相应的控制载荷是否存在,本文针对该问题,并结合实际试验情况,对控制载荷的存在性从理论上进行分析。
1 目标响应与控制载荷间传递关系分析
经过有限元离散化,频域内结构的动力学方程为:

式(1)中:M、C、K分别为结构的质量、阻尼和刚度矩阵;Xa(ω)、Xv(ω)、Xd(ω)分别为结构的加速度、速度和位移响应;F(ω)为结构受到的外载荷。
振动环境试验中,常关注正弦振动和随机振动两种工况,且考虑到实际试验中常关注结构的加速度响应,正弦振动下,结构加速度的谐响应为:

式(2)中:H(ω)为载荷与加速度响应之间的传递函数矩阵。

记c为所关注的多点响应集合,其维数为m;f为载荷施加的节点集合,其维数为n。则关注点c的加速度谐响应为:

其中,Hc(ω)为H(ω)中与c所对应的行和f对应的列所构成的矩阵,其维数为m×n。
对于随机振动而言,关注点响应的功率谱密度矩阵Pc(ω)为:

式中:dω为频率分辨率[19],为圆频率。
由于谐响应分析是随机振动的基础,可由谐响应推导出随机振动的响应,因此在讨论多点随机振动下的控制载荷存在性时,可通过多点谐波激励分析开展研究,具有等价性。
2 控制载荷存在性分析
将式(4)写成完备矩阵形式,如式(6)所示,其中元素的虚部反映了响应的相位信息。

记传递函数矩阵Hc的增广矩阵Hz为:

另记Hc和Hz的秩分别为Rc和Rz,以下基于矩阵论中增广矩阵对解的判定研究,讨论多点响应等效时控制载荷的存在性问题。
2.1 同时控制响应幅值和相位
1)Rc=Rz=n,即传递函数矩阵的秩与其增广矩阵的秩相等,且为满秩。对实际工程结构而言,一般意味着响应控制点数量与激励数量相等,此时式(6)存在唯一解[20],控制载荷可由式(8)计算获得。

将式(6)的虚部进一步改写为相位角的形式,则有:
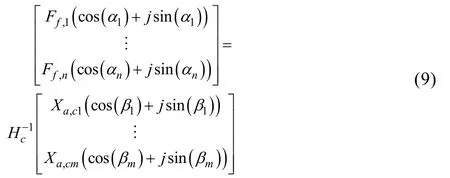
式中:α和β分别为激励与响应的相位角。
2)Rc=Rz<n,对于工程结构的传递函数矩阵而言,一般意味着响应控制点数量小于控制载荷数量,此时式(6)存在无穷解[20]。
将式(6)改写为:
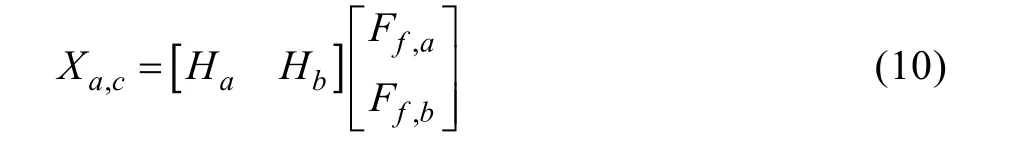
式(10)中:Ha的维数为m×m,Hb的维数为m×(n‒m)。将式(10)展开为:

当Ff,b=0时,式(11)就退化到m=n时的情况。需要指出的是,Ha可由H矩阵中任意m列元素构成。这种组合方式很多,相比m=n时的情况,提供了更丰富的加载组合方式。因此,控制载荷也不唯一,有利于多点激励时响应控制的实现。
3)Rc<Rz,对于工程结构的传递函数矩阵而言,一般意味着响应控制点数量大于控制载荷数量,即期望通过少量的加载设备实现对多个点的响应的控制,此时式(6)的解往往不存在[20]。
2.2 仅控制响应幅值
以上讨论都是从数学角度出发,是严格意义上的响应等效分析,要求响应功率谱密度矩阵Pc(ω)中的所有元素都得到控制,每个元素实部和虚部都等效。从动力学意义上来说,则表现为多个测点的响应幅值以及多个测点之间的相位关系都是固定的,对控制精度要求较高,实现难度较大。目前在工程应用中的实际情况是只控制测点响应的幅值。以随机振动试验为例,即只控制式(5)中功率谱密度矩阵Pc(ω)的对角线元素,并不控制多个控制点之间响应的相位,即Pc(ω)中的非对角线元素(互谱),多个控制点之间的相位可以是随机的,因此等效程度有所放宽,此时控制载荷的存在性结论将发生变化:
1)Rc=Rz=n时,即在只控制响应自谱的情况下,加载设备数量与响应控制点数量相同时,由于式(9)中的β具有任意性,因此控制载荷Ff并不唯一,这种特性便于多点激励时响应控制的实现。
2)Rc=R<n时,即在只控制响应自谱的情况下,加载设备数量大于响应控制点数量时,与上述分析类似,控制载荷仍然不唯一。
3)Rc<Rz时,即在只控制响应自谱的情况下,加载设备数量小于响应控制点数量的情况。实际试验中,往往也只能基于有限的加载设备搭建多维振动试验系统,那么在不控制多点响应之间相关性这种相对弱化的条件下,控制载荷与等效响应幅值之间的传递关系如何?若能够通过少量的加载设备实现对多个点响应的控制,将具有重要的工程应用意义。
以m=3、n=2,即两点激励、三点响应控制为例,对控制载荷从数值求解的角度进行分析。为便于分析,取频率分辨率dω=2π,即1 Hz,得到3个目标响应点的响应功率谱密度Pcm(m=1、2、3)的表达式为[21]:
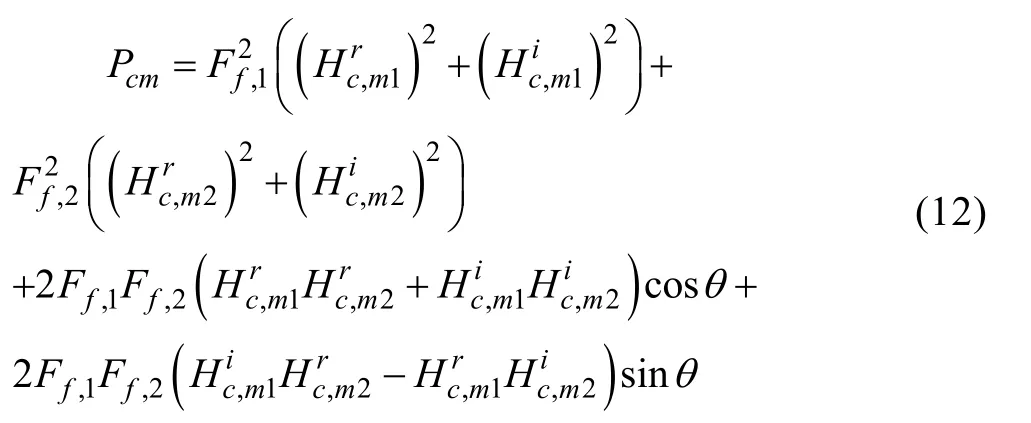
其中,θ=α1‒α2,为两点激励之间的相位差。式(12)表明,两点激励时,影响3个控制点响应的载荷参数有3个,即2个振动台的台面响应功率谱和,以及它们之间的相位差θ。式(12)也表明了响应功率谱与控制载荷之间的非线性关系,难以参考非齐次线性方程组解的存在性理论,说明控制载荷不存在。
文[21]中采用优化算法对梁结构在两点激励、三点响应控制的控制载荷进行了数值模拟,结果表明,控制载荷在某些频段内并不存在,而在某些频段范围内控制载荷仍然可以获得,能够满足控制要求,凸显了问题的复杂性。
上述分析是从数学意义上讨论控制载荷的存在性,但对于实际工程而言,当加载位置的选择点不合理。如处于某阶模态的振型节点附近,响应控制点位于振型值较大的位置时,在该模态频率附近要实现多点响应控制将十分困难,或者说对推力的要求往往是非常大的,导致无法实现。以下通过某典型结构的多种工况的数值仿真对该情况进行分析说明。
3 数值模拟
3.1 仿真模型
如图1所示筒状结构,材料为钢,长度为2000 mm,小端内径为300 mm,大端内径为536.8 mm,筒壁厚8 mm,质量约280 kg。试验中采用大小两端柔索悬挂模拟自由边界条件,响应控制点为A1—A3,可根据不同的控制需求选择控制点组合,多点激励可供选择的加载点为B1—B5。载荷类型为力,坐标方向如图1所示,轴向为x方向,横向为y方向,响应控制和加载的方向均为y方向。
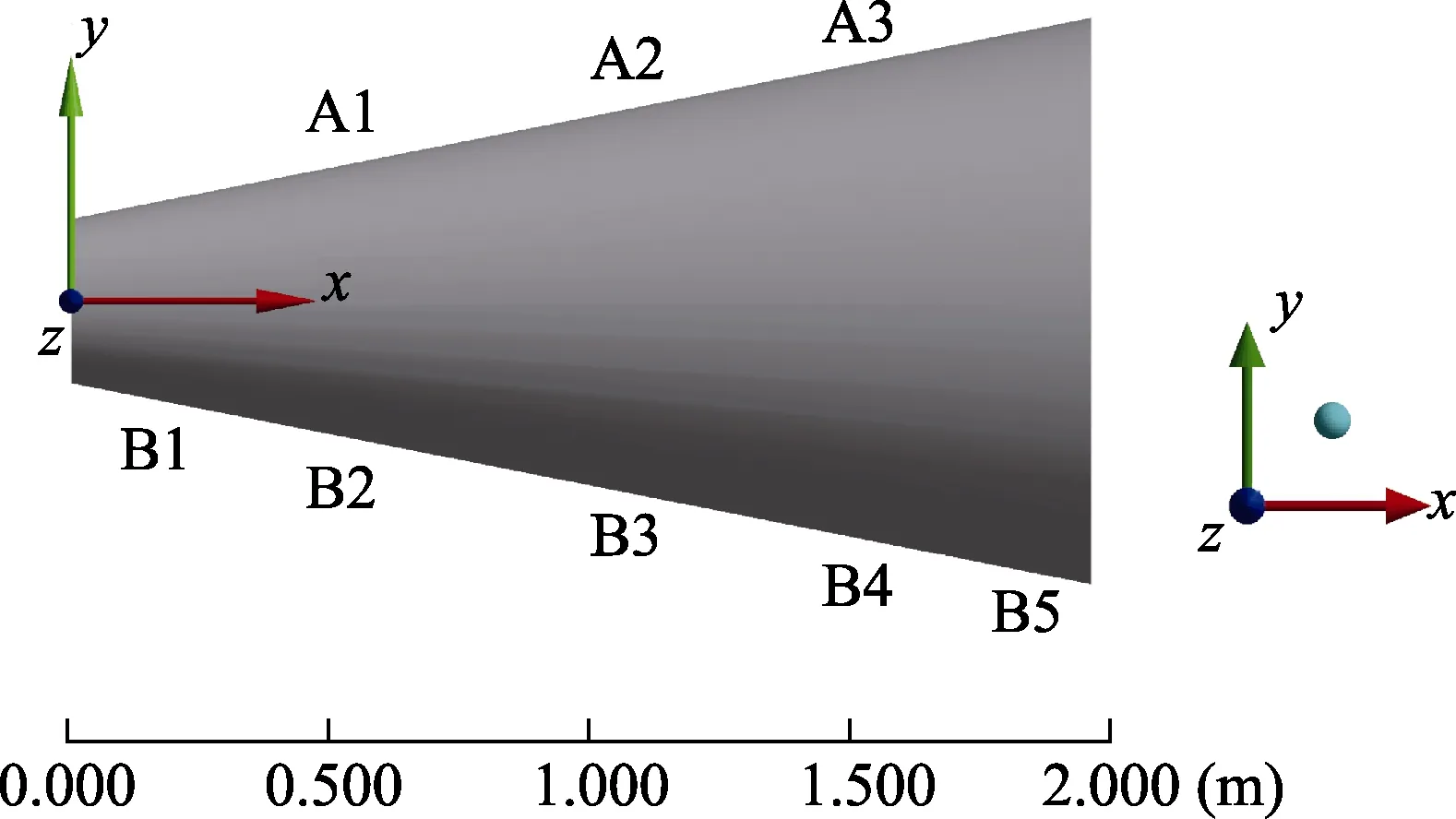
图1 筒结构多点激励示意Fig.1 Multi-point excitation sketch of tube shape structure
研究中设置的多种仿真工况见表1。其中,谐波载荷和随机振动载荷下的目标响应控制曲线如图2所示。谐波载荷激励频率范围为5~1000 Hz;随机振动下,激励频率范围为10~1000 Hz,频率分辨率为0.5 Hz,且3个控制点的响应功率谱密度曲线设置一致。
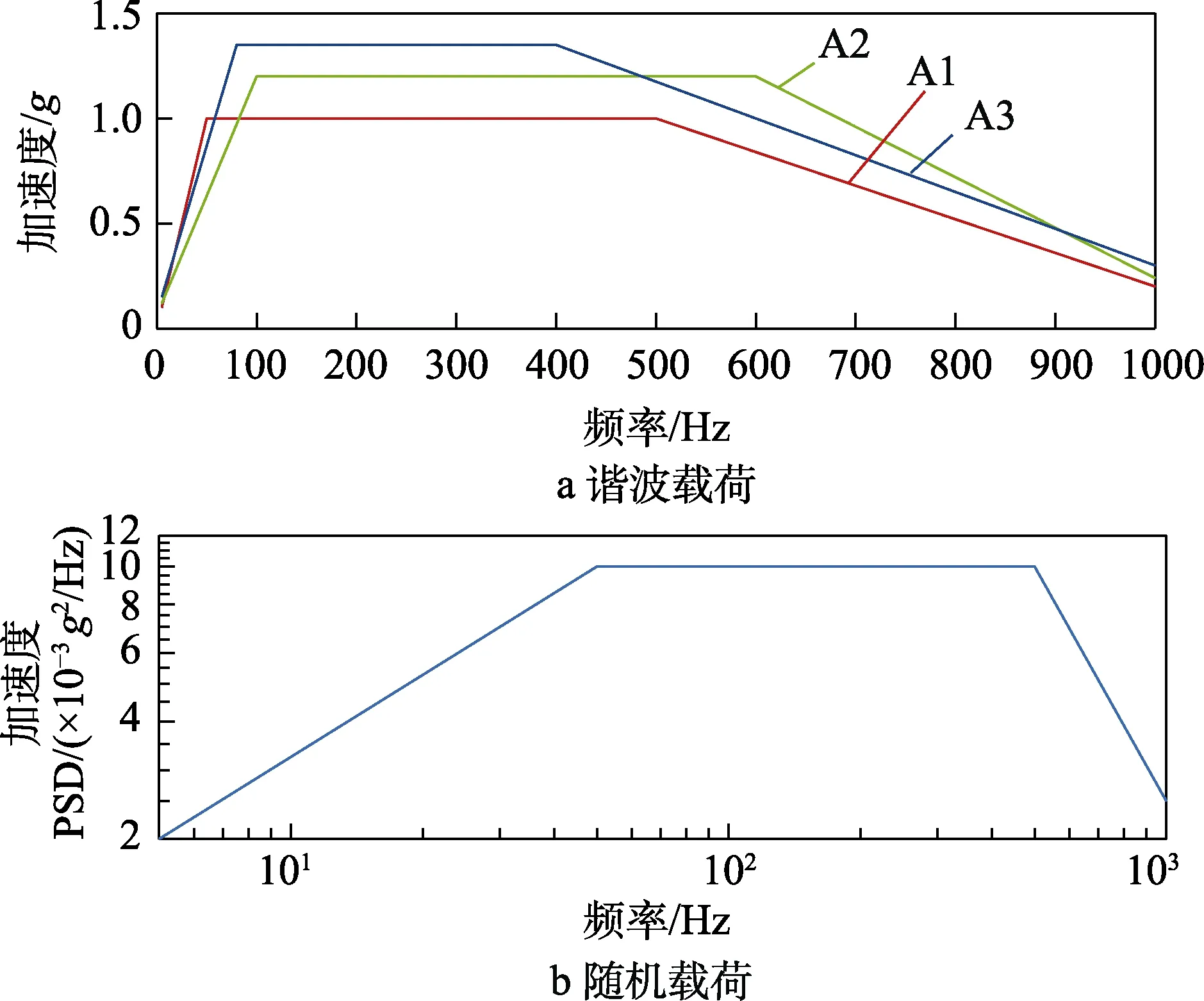
图2 各控制点的目标响应曲线Fig.2 Target control point response: a) harmonic excitation;b) random vibration
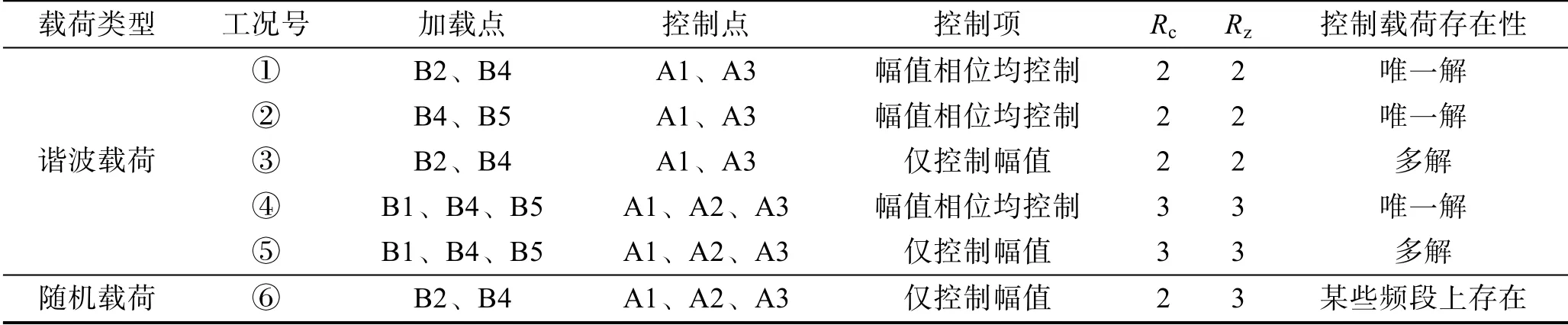
表1 控制载荷数值模拟工况Tab.1 Numerical simulation working condition of control load
3.2 仿真结果
工况①、②下,控制载荷的幅值和相位角的频谱曲线如图3所示。为便于分析,考虑2个控制点响应之间相位差为0,此时,控制载荷是唯一的,不同的加载点选择,所需要的控制力谱也不同。另外也可以看出,工况②下所需的控制载荷幅值要比工况①下大得多,这说明在试验中,合理地选择加载点能够充分利用设备推力加载能力,以达到试验目的。
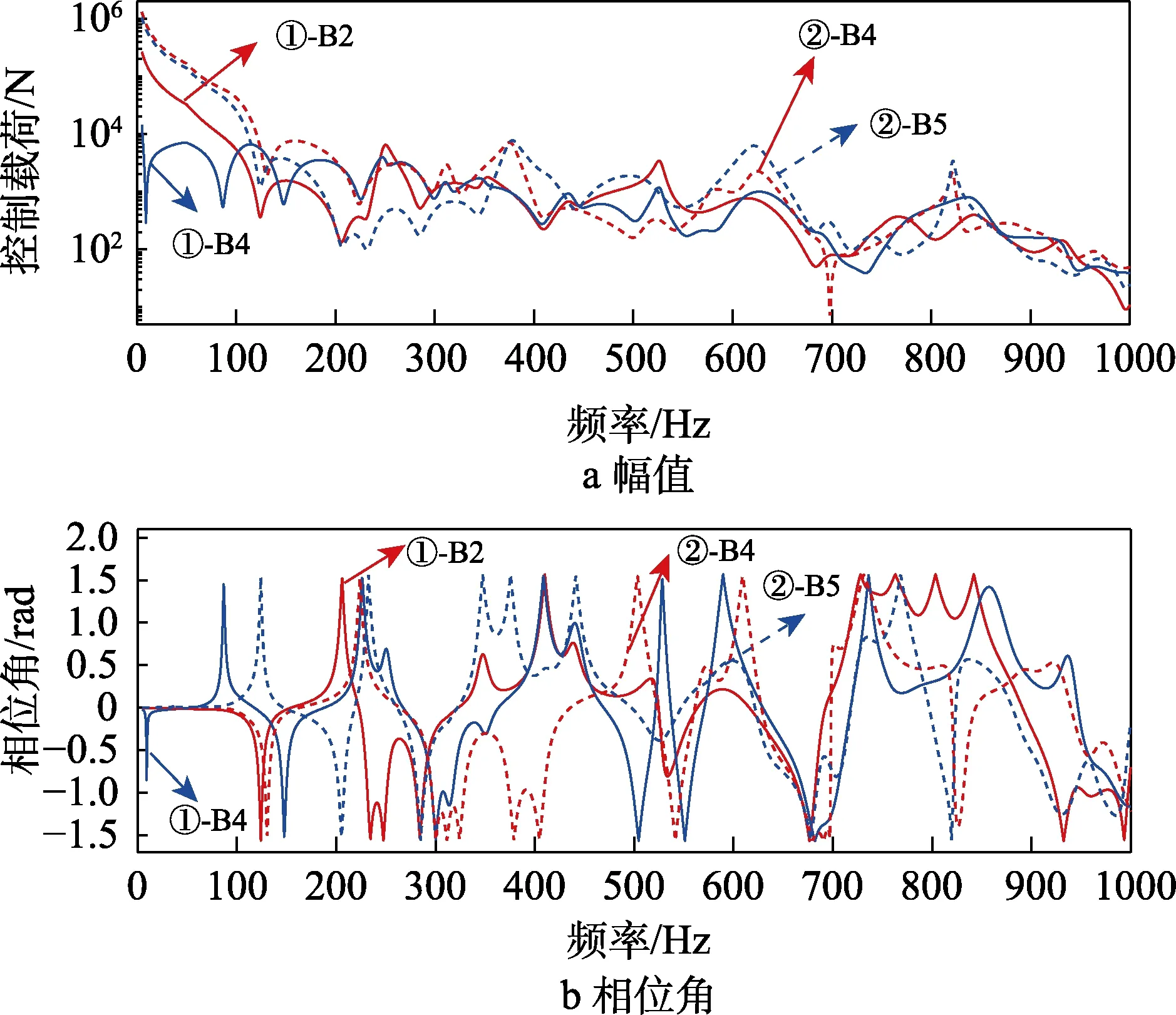
图3 工况①、②的控制载荷Fig.3 Control load of working condition ①,②: a) amplitude;b) phase angle
工况③下,仅控制A1、A3两点谐响应幅值谱时的控制载荷曲线如图4所示,图中结果只是其中的一种解的情况。
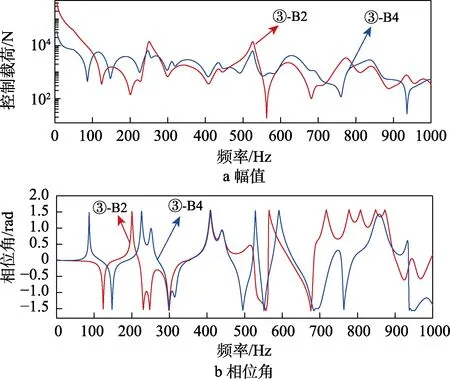
图4 工况③的控制载荷Fig.4 Control load of working condition ③: a) amplitude; b)phase angle
谐波激励下,对A1、A2、A3的幅值和相位均控制时的控制载荷如图5所示,3个响应点之间的相位差设置为0。图6则给出了仅控制幅值谱时的控制载荷,与工况③类似,也只是多解中的一种情况。

图5 工况④的控制载荷Fig.5 Control load of working condition ④: a) amplitude; b)phase angle
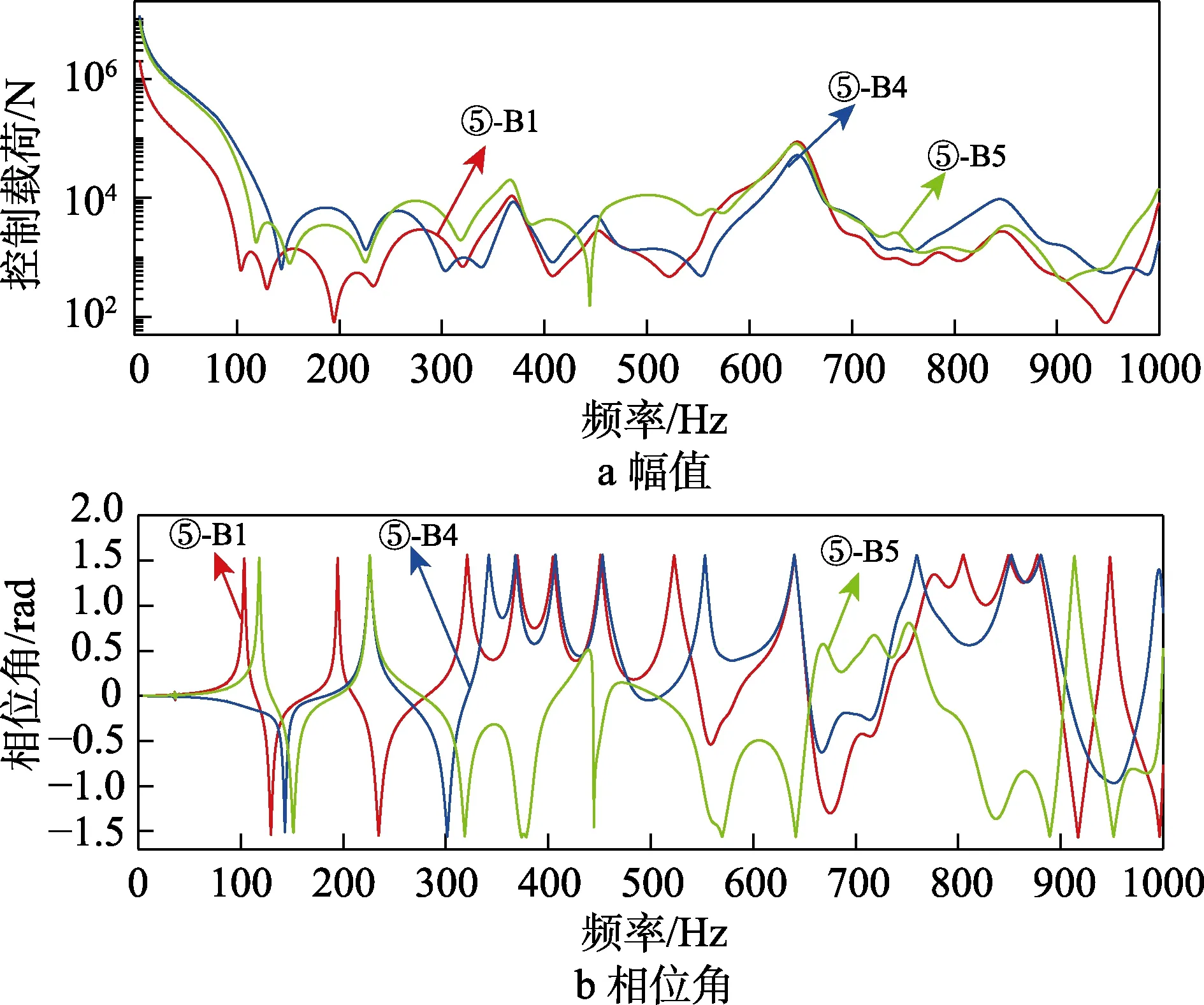
图6 工况⑤的控制载荷Fig.6 Control load of working condition ⑤: a) amplitude; b)phase angle
随机载荷下,两点激励、三点响应控制的控制载荷如图7所示。只控制三点响应的幅值,数值模拟中采用遗传优化算法,对两点激励的幅值以及它们之间的相位差进行优化,同时,考虑了实际随机振动试验中控制容差为±3 dB。可以看出,在诸多频段范围内,仍然能找到满足控制容差的控制载荷。
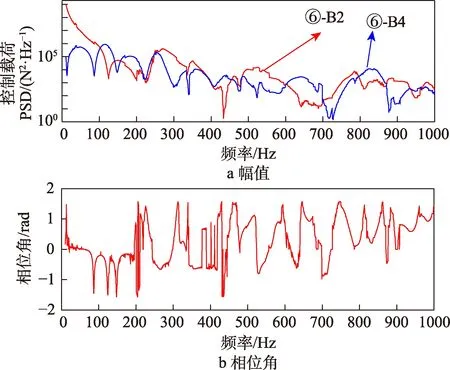
图7 工况⑥的控制载荷Fig.7 Control load of working condition ⑥: a) amplitude; b)phase angle
图8 中,123 Hz附近的控制响应的超差比较严重,主要表现为A1和A3点响应较大,而A2点的响应较小。通过模态分析,可以观察到在该频率点处存在第六阶模态,频率为121.6 Hz,其振型如图9所示。A1、A2、A3各点的振型值分别为4.82×10‒4、3.38×10‒5、4.99×10‒4,可见也正好表现为A1、A3点响应大,A2的响应小的特点,造成在模态频率附近难以控制。
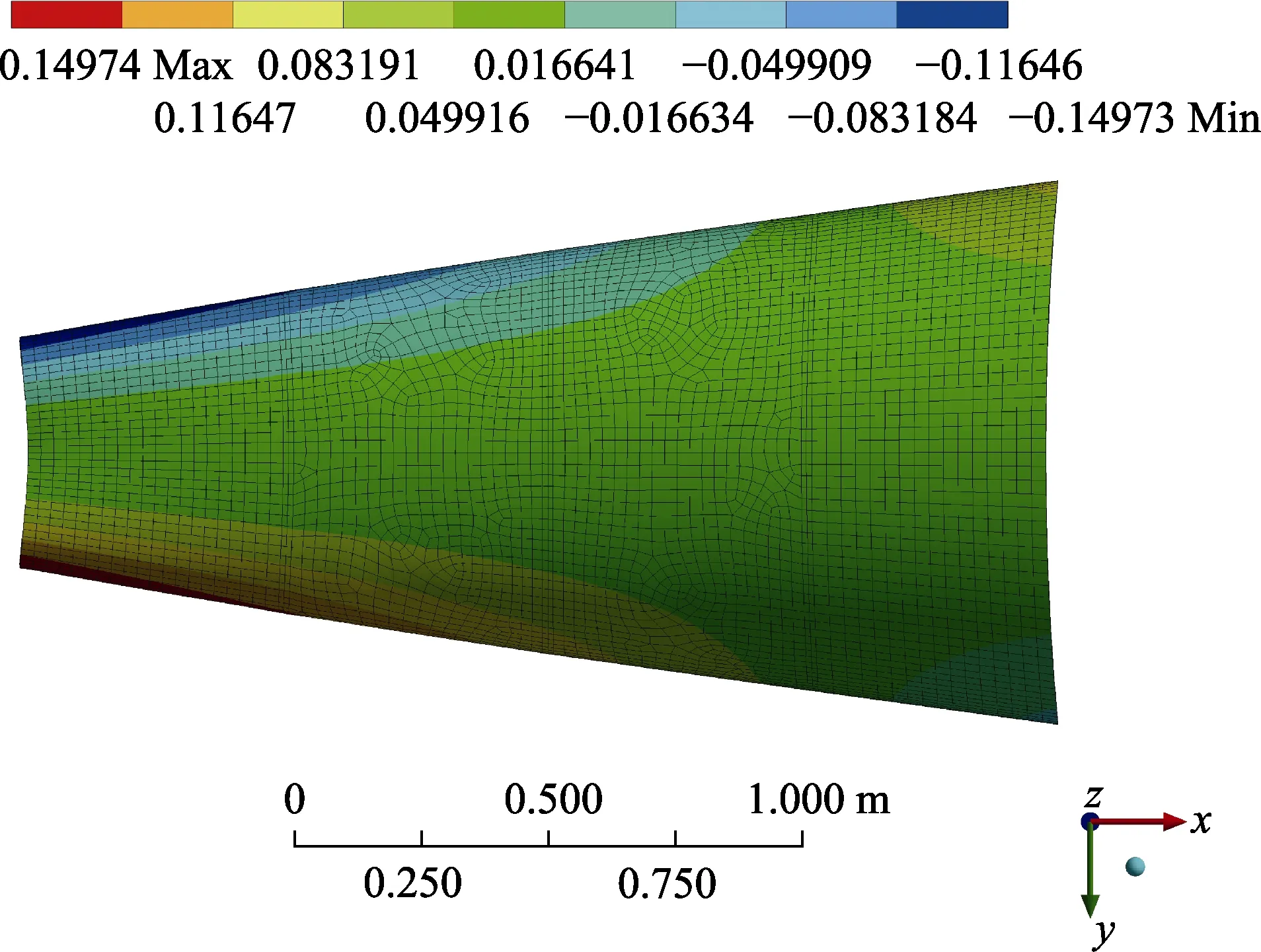
图9 第六阶模态振型Fig.9 The sixth mode shape
从图8中也可以看出,在575 Hz左右,控制精度较高,而在123 Hz处,控制超差严重。将式(12)进一步改写为:
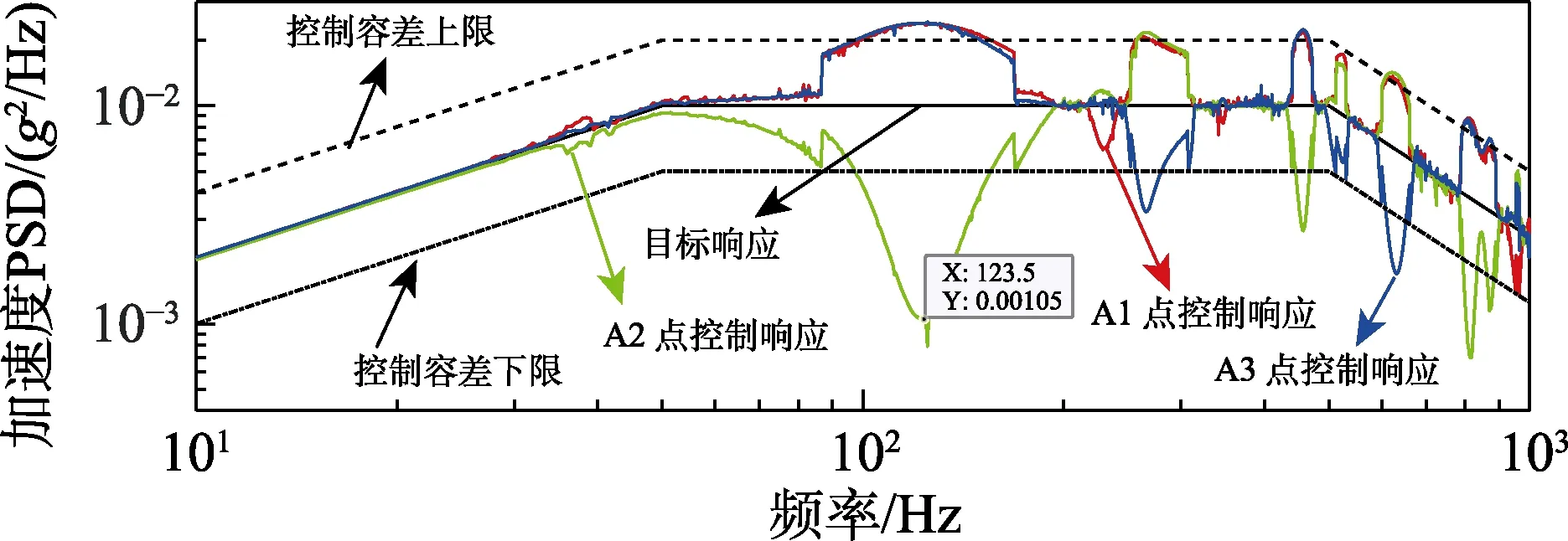
图8 工况⑥控制载荷产生的响应与目标响应对比Fig.8 Comparison of control load caused response with target response in working condition⑥
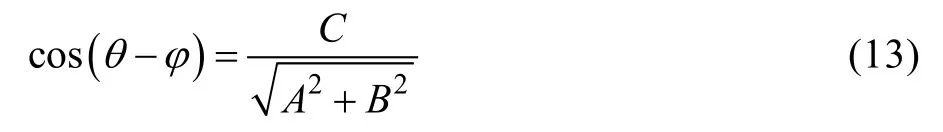
其中:
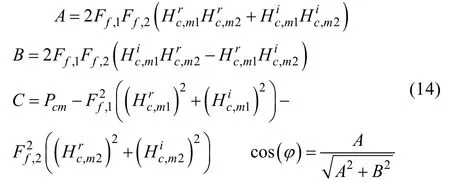
进一步得到:

式(14)中,m=1、2、3,根据式(15),给出了在123 Hz和400 Hz处式(12)数值解的分布曲面,如图10所示。
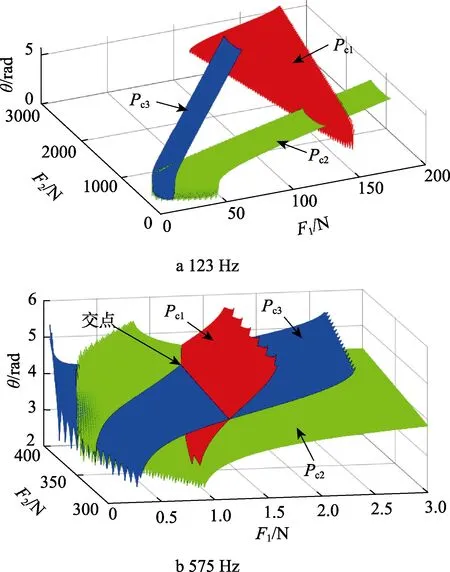
图10 不同频率点上控制载荷解的分布Fig.10 Solution distribution of control load at different frequencies
由图10可见,在123 Hz处,3个解的分布曲面无交点,即无精确控制解,优化过程中超差也较为严重。在575 Hz处,3个解的分布曲面有交点,有精确控制解,优化仿真过程中,偏差很小。
4 结语
从结构动力学的载荷与响应之间的传递关系出发,基于谐响应分析,将传递函数矩阵及其增广矩阵的秩的大小关系对比作为控制载荷存在性的判据。从广义上给出了多点激励下,同时控制响应幅值和相位时控制载荷的存在性,并结合典型结构进行了控制载荷的数值模拟。结合实际振动试验中只控制响应幅值的情况,给出了仅控制幅值时控制载荷存在性结论,尤其是针对利用少量加载设备实现多点响应幅值控制的情况,其控制载荷在某些频段上仍然存在。
