林木联合采育机蜂窝结构进料辊关键技术与应用性能研究

2021-08-13曲云飞朱旭晨

安徽农业大学学报 2021年3期

曲云飞，王典*，朱旭晨

曲云飞1,2，王典1,2*，朱旭晨1,2

(1. 北京林业大学工学院，北京 100083；2. 林业装备与自动化国家林业和草原局重点实验室，北京 100083)

针对机械化采伐作业中减少木材损伤的问题，提出一种基于辊型双V蜂窝结构的进料辊。结合相关的数学公式，推导出了辊型双V蜂窝结构的动态冲击模型，并通过有限元仿真结果得到了验证。对伐木工况低速冲击下辊型蜂窝的力学与吸能特性、动态响应、结构稳定性和结构效率等应用技术指标进行探究，并引入不同结构的辊型六角蜂窝进行参照对比。低速冲击下，辊型双V蜂窝相较于辊型六角蜂窝负泊松比效应更明显，结构效率更高且抗冲击性更强，结构稳定性更好，接触力更均匀。各辊型双V蜂窝结构冲击至0.3时的各应力指标均满足1 600 kg以下树木采伐工况需求。这为蜂窝结构进料辊的机械化应用与减少原木损伤提供了参考。

采育机；进料辊；农林机械；树木损伤

近些年来，以林木联合采育机为代表的林业装备得到了广泛的使用。与人工采伐相比，借助林木联合采育机的机械化采伐具有低人员劳动强度、高生产效率、低生产作业事故率低和高生态效益等优点[1]。许多研究通过预测产量建模[2]、离散元建模[3]和现场人工观测[4]等方法对原木与采伐相关的技术进行研究。进料辊是林木联合采育机的主要工作部件。现伐木作业中广泛使用的为钢制进料辊（steel feeding roller，SFR），外缘均布钢齿。在林木联合采育机伐木作业过程中，通过钢齿与原木的啮合，转动以提供驱动动力。同时，伐木作业中存在着原木木质损伤与进料辊易过度磨损的问题[5]。采伐原木木质损伤很大程度降低了原木的利用价值与经济效益[6]。Sveningsson[7]评估了伐木作业中不同类型进料辊与环境温度对木材损伤的影响关系。Connel[8]通过实地调查的方式，对机械化采伐过程中木材损伤的问题节点进行了全面分析。指出造成的木材损伤主要来自于木材驱动的物理损伤与测距损伤。造成这些损伤的主要原因是缺乏足够的摩擦力，进料辊的接触压力过大。Strandgard等[9]研究了机械化采伐中原木损伤导致的桉树树皮产量降低的问题。为了保护树皮不受到严重的木材损伤，进料辊的动作液压缸压力会降低，进而降低了林木联合采育机的作业效率。卢杰等[10]结合Pro/Engineering软件提出一种通过机械阻尼结构以减少木材损伤的进料辊。现有的研究没有对进料辊本身的结构进行改进，难以满足减少原木损伤的需求。

负泊松比蜂窝结构材料则因具有在受压缩时受压区域出现局部致密化的现象而受到广泛关注[11]。凭借这种独有的物理变形特点，负泊松比蜂窝结构具有轻质、更强的韧性、更好的抗剪强度与抗冲击吸能响应特性，从而在工程、电子与航空航天等领域广泛应用[12-14]。作为一种重要的负泊松比微观结构，双箭头负泊松比结构最早由Larsen等[15]通过拓扑优化方法所获得。Álvarez等[16]对现有的几种负泊松比蜂窝结构的力学特性进行了详细的分析比较。结果显示，相对于其他蜂窝结构，双箭头蜂窝与内凹蜂窝结具有更大的体积与面积减缩率，更高的泊松比与等效杨氏模量。Kelvina等[17]研究了圆周蜂窝的横向剪切和正交各向异性对模态密度的影响，并建立了相关的数学表达模型。Baranowski等[18]为了提高轻型装甲车的强度和阻力，提出了六角蜂窝状复合车轮。结果表明，该应用蜂窝复合材料的车轮能有效降低爆破冲击能量并提高防护安全性。

本研究针对林木联合采育机蜂窝结构进料辊的应用与伐木工况需求，对双箭头蜂窝胞元结构进行改造，提出一种新型蜂窝结构并命名为双V附翼型蜂窝。结合现有的进料辊设计，提出一种基于双V附翼型蜂窝（double V-wings honeycomb，DVWH）的林木联合采育机进料辊，辊型双V蜂窝结构作为进料辊的柔性蜂窝填充结构。辊型双V蜂窝结构的动态冲击模型可作为蜂窝设计选择的规律与预测的参考。对伐木工况低速冲击下辊型双V蜂窝结构的力学与吸能特性进行探究，并引入不同胞元结构的六角蜂窝进行蜂窝进料辊应用性能参照对比。从辊型蜂窝结构的固体力学、冲击吸能、结构变形模式、驱动系统受力、结构稳定性和结构效率等方面进行关键技术与应用性能评估比较。

1 林木联合采育机蜂窝结构进料辊与理论分析模型

1.1 辊型双V蜂窝结构与胞元

双V附翼型蜂窝胞元的附翼为蜂窝圆周型的组合提供了足够的连接节点与连接弧度，解决了此类蜂窝的圆周型连接问题。辊型双V蜂窝结构是蜂窝结构进料辊的主要组成部分，因此对蜂窝结构进料辊的研究主要集中辊型蜂窝结构的应用性能指标评估。选定已应用林木联合采育机进料辊的填充蜂窝结构的参数作为辊型双V蜂窝的初始蜂窝样本[19]，并记做=1.0。定义为等效处理后蜂窝的宽度或厚度与初始蜂窝（1.0）的比值，记为n=l/l=t/t(0.5–2)。代表不同蜂窝下的参数，l或t表示不同蜂窝的宽度或厚度。因此，与蜂窝的胞元密度有关，即不同的蜂窝具有不同的胞元密度。如图1 (b)所示，双V附翼型蜂窝胞元可由以下变量进行描述，分别为：胞元跨度L、胞元宽度l、胞元附翼宽度、胞元壁厚t、胞元V型结构内外夹角θ、θ与厚宽比ϕ=t/l(0.5–2)。=1.0辊型双V蜂窝胞元参数分别为θ=30°、θ=75 °、l=29 mm、l=8 mm与t=5 mm辊型双V蜂窝可通过以下设计变量进行描述：结构层数L，层胞元数N，结构厚度，辊型双V蜂窝半径R轮辋半径R与辊型双V蜂窝填充层半径R并且有R=R+R。受辊型双V蜂窝的半径，层胞元数N与等参数影响。

1.2 辊型双V蜂窝等效关系理论模型

根据多孔材料理论（CMT），蜂窝结构的相对密度可由代表性胞元实体承载部分面积与代表性胞元总截面面积的比值确定。辊型双V蜂窝结构相对密度推导则有：

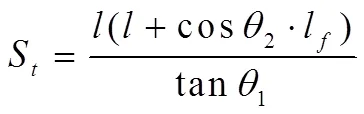
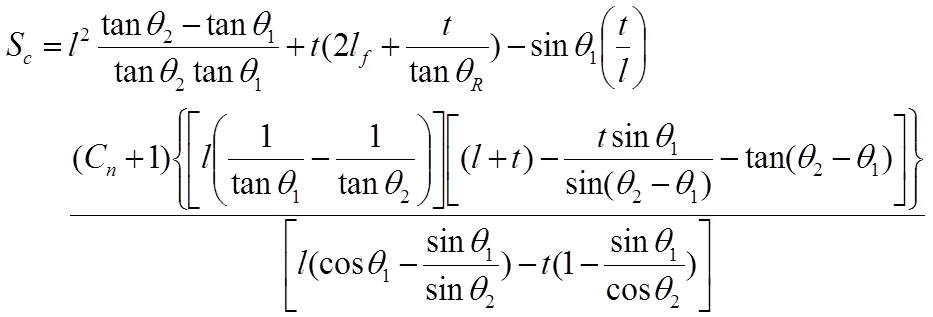
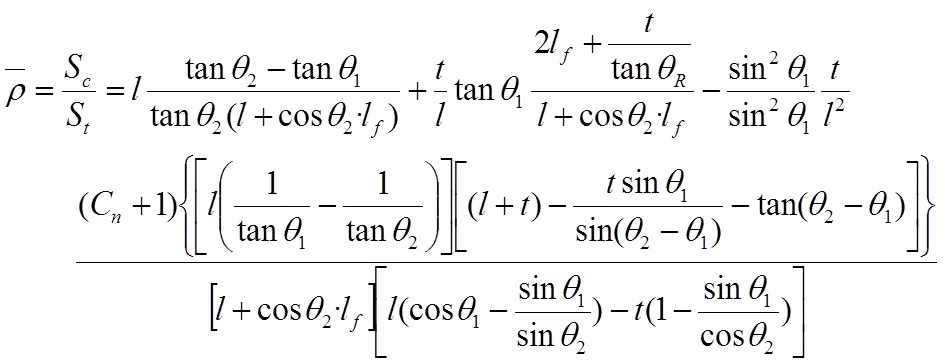
式（1）—（3）中，S为RDWH代表性胞元实体承载部分面积，S为RDWH代表性胞元总截面面积。结合Qiao等[20]给出的弹塑性压实应力公式（4），低速冲击下的辊型双V蜂窝结构的动态崩塌平台应力有：

式中，ε为辊型蜂窝结构名义应变，ρ为蜂窝结构基体材料属性，为低速冲击速度。

1.3 辊型双V蜂窝与辊型六角蜂窝有限元模型

通过控制辊型双V蜂窝的厚宽比，建立出3个具有几何倍数关系的辊型双V蜂窝结构有限元模型，分别为=0.5，=1.0，=2.0蜂窝，如图1 (a)所示。辊型双V蜂窝结构尺寸参照LAKO 43伐木机适配钢制进料辊。3种胞元密度辊型双V蜂窝具有相同的R=60 mm和=110 mm，相近的R和R，不同的胞元尺寸、N和L，如表1所示。

表1 辊型双V蜂窝结构胞元与试样参数

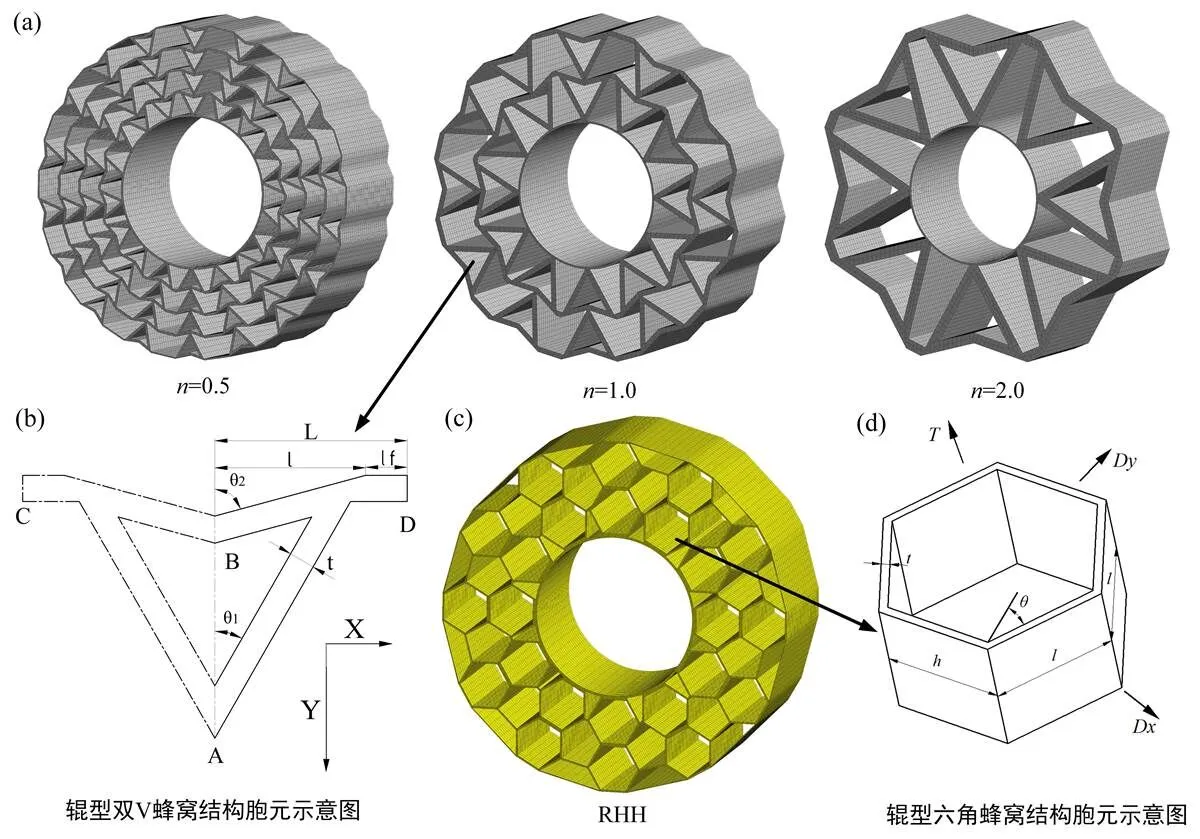
图1 (a)辊型双V蜂窝结构有限元模型，(b) 辊型双V蜂窝结构胞元示意图，(c)辊型六角蜂窝有限元模型，(d) 辊型六角蜂窝结构胞元示意图

Figure 1 (a) Finite models of RDWH, (b) Schematic of RDWH unit cell, (c) Finite model of RHH, (d) Schematic of RHH unit cell

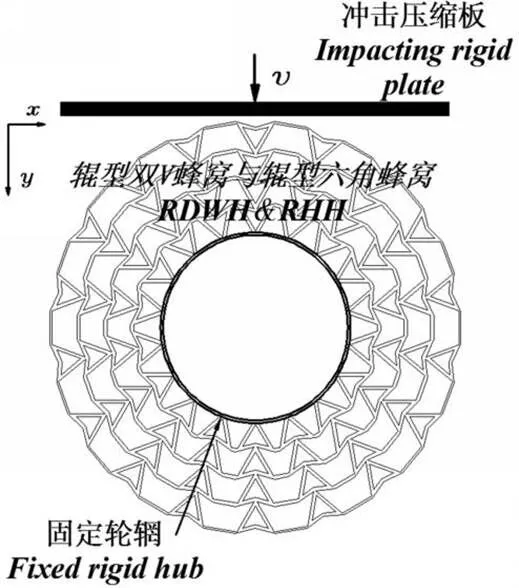
图2 辊型蜂窝结构冲击加载示意图

Figure 2 Diagrammatic sketches of roller honeycomb under dynamic impact in logging

本研究采用ANSYS/LS-DYNA对不同胞元密度下的辊型双V蜂窝的低速冲击特性进行显示动力学分析。根据林木联合采育机的工作原理，产生的低速冲击主要由两个因素引起，一是进料辊与原木夹紧的定位过程，一般速度范围1.2 m·s-1～2 m·s-1。另一个是原木进给过程中凸出的树结对旋转中进料辊的冲击阻力，冲击速度小于1 m·s-1。两种冲击速度发生在伐木作业中的不同阶段。选择临界速度2 m·s-1作为辊型蜂窝结构垂直方向的仿真速度。将辊型蜂窝结构受冲击物体简化为刚体冲击板，其质量远大于试件质量，冲击速度控制均匀。选定典型的六角蜂窝的辊型蜂窝填充层作为辊型双V蜂窝的蜂窝仿真对照组。辊型六角蜂窝有限元模型与胞元示意图分别如图1 (c)和(d)所示。辊型六角蜂窝的胞元排列形式参照的六角蜂窝轮胎结构设计[15]。辊型六角蜂窝的结构与1.0蜂窝相似，两者具有相近的胞元大小、规则胞元数量、结构层数L与结构半径R。辊型六角蜂窝的参数为=23.5 mm、π/33.2 mm110 mm和163 4677.159 mm3。辊型六角蜂窝的冲击边界条件和试样材料基体与辊型双V蜂窝相同。文中所述的辊型蜂窝结构是辊型双V蜂窝与辊型六角蜂窝的合并总称。

在试件受冲击过程中，辊型蜂窝试件放置于刚体冲击板的正下方。辊型蜂窝结构嵌入了固定刚体轮辋。每个辊型蜂窝试样的节点受异面限定，结构外圈等剩余部分是自由无限制的。刚体冲击板分别沿轴和轴正方向冲击，冲击速度为2 m·s-1。辊型蜂窝冲击过程中只有压缩变形而无旋转等动作，加载示意图如图2。基于采伐冲击工况需求与材料断裂强度考虑，设定辊型蜂窝压缩比为单边蜂窝结构半径与其辊型蜂窝比值，选用0%～50%的压缩比区段进行仿真。计算中选用聚氨酯作为辊型蜂窝结构试样材料基体[21]，并假定基体材料采用理想弹塑性模型，材料参数为：密度ρ=950 kg·m-3，杨氏模量=1 100 MPa，泊松比0.42。假定试样基体材料属性不受基体速率改变影响。胞元选用Shell163单元，每个壳单元元素设定相同的长度与厚度属性。每个胞元壁单元元素数受和θ变化而改变。对有限元数值分析中的网格灵敏度进行了网格收敛分析。当RDWH与RHH的节点数分别超过39 712和24 316时，峰值应力值可以得到收敛结果。因此，为提高仿真动力响应的精度，分别选定64 920节点和51 274个节点网格作为RDWH和RHH的精细网格。每个胞元壁面接触方式设定为单一接触面。动态压缩变形过程中胞元壁之间的外面接触设定为自接触。忽略接触摩擦的影响，试件与刚体接触设定为面面接触形式。

2 蜂窝进料辊关键技术和应用性能指标

2.1 辊型双V蜂窝动态冲击理论模型验证

根据式（3）和（5），图3显示了辊型双V蜂窝结构动态崩塌平台应力理论计算结果与有限元仿真分析结构的比较。1.0蜂窝的σ理论值与仿真值一致性较好，在ε之后出现蜂窝侧向壁的压实，仿真应力出现陡增。0.5和2.0蜂窝的有限元仿真结果略高于与低于计算结果，可能是由于不同胞元结构层数造成的影响。0.5、1.0和2.0蜂窝的理论计算值与有限元仿真结果的最大平均误差别分为10.1%、7.8%和20.1%。总的来说，辊型双V蜂窝结构的理论计算值与有限元仿真结果吻合较好，辊型双V蜂窝动态冲击模型得到了验证。

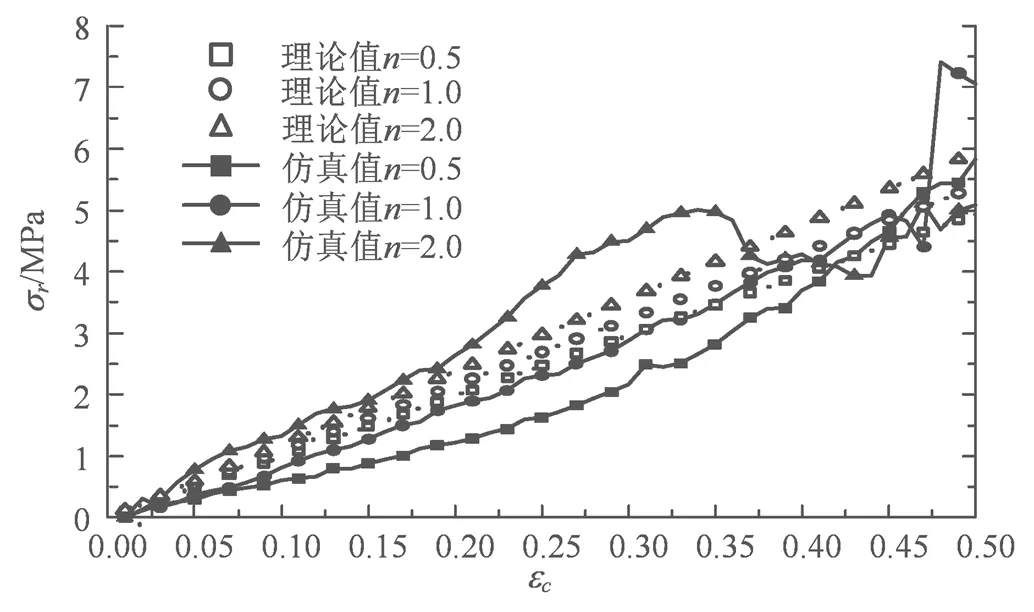
图3 辊型双V蜂窝结构动态冲击理论模型验证

Figure 3 Diagrammatic sketches of roller honeycomb for dynamic impact theoretical model

2.1 辊型蜂窝力学吸能比较与评估

辊型蜂窝结构的力学与吸能数值曲线如图7所示。力学与吸能数值取自于辊型蜂窝压缩比50%区间的最大值。辊型蜂窝压缩位移量在32.2～65.1 mm区间内，冲击时间在0.019 4～0.025 6 s区间内。其中辊型蜂窝结构应变指的是辊型蜂窝平均变形位移（冲击板的位移）D与辊型蜂窝结构半径R的比值，则有ε=D/R。

图4 辊型双V蜂窝与辊型六角蜂窝力学与吸能数值曲线

Figure 4 Mechanical and energy absorption numerical curves of roller honeycombs

辊型双V蜂窝与辊型六角蜂窝的力学与吸能数值曲线如图4所示。其中辊型蜂窝应力展现出两个应力平台，分别是在0～0.2左右的弹性应力平台与0.2～0.5的应力长平台。如图4（a）与（b）所示。仿真数值可以看出各辊型双V蜂窝的力学曲线变化趋势具有一致性，证明等效关系下的辊型双V蜂窝具有相似的力学特性。正应力曲线表示辊型蜂窝正方向冲击承载性。切向应力曲线代表辊型蜂窝变形部分受到的总切向应力。可以发现辊型双V蜂窝吸能量变化趋势随的增大而增大，2.0蜂窝吸能量数值最高。由于辊型双V蜂窝受冲击时的负泊松比效应，造成结构的局部应力增强，使得辊型双V蜂窝的应力性能均高于辊型六角蜂窝，且辊型六角蜂窝吸能平台平缓，吸能量均低于辊型双V蜂窝。各辊型双V蜂窝结构=0.3时的各应力指标均满足1 600 kg以下树木采伐工况需求。

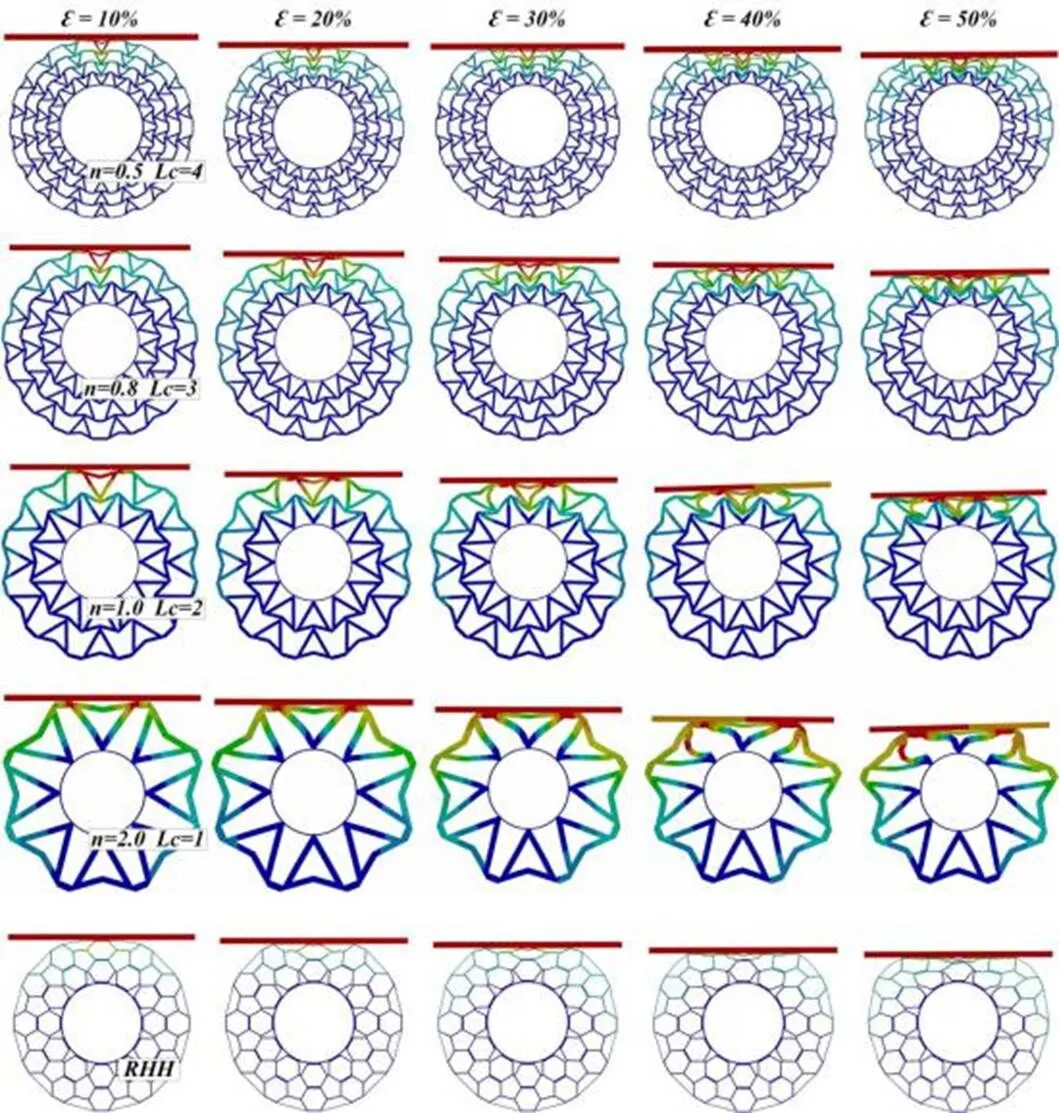
图5 低速冲击下辊型蜂窝的变形模式

Figure 5 Deformation mode of roller honeycombs under low-speed impact

图6 辊型蜂窝轮辋反力与结构接触力变化曲线

Figure 6 The fluctuating curves of roller honeycomb for force reaction and contact force

2.2 辊型蜂窝变形模式与动态接触响应

图5是辊型蜂窝在=2 m·s-1低速冲击下的变形模式。不同下的辊型双V蜂窝辊型蜂窝变形模式较为一致，受冲击过程中，周侧胞元向中心受压区域集聚，结构整体均有收缩，展现出负泊松比现象。当=0.1～0.2时，辊型蜂窝中心列的受压胞元对两侧连接的胞元有拉拽行为，胞元间连接的附翼挤压弯曲多为拉压变形，有效分散了应力，使胞元变形分布平均。当辊型蜂窝压缩至=0.3～0.4，中心列胞元上端壁受压展开与板接触，胞元间产生转矩与横向交错，部分胞元壁下方出现弯曲变形，胞元变形变得复杂化且不对称。随着压缩的继续进行至=0.5，中心列胞元上端壁和附翼与刚性压缩版近似压实。=0.5辊型蜂窝胞元尺寸较小，胞元排列紧密密度大，结构层数较多，所以胞元变形排列整齐多为拉压变形，刚性压缩板接触强度均匀。=2.0辊型蜂窝胞元弯曲变形程度大且不对称，胞元较早进入塑性变形阶段而易于压溃。因此，胞元尺寸、胞元密度与结构层数都对辊型蜂窝冲击变形模式产生影响。

辊型六角蜂窝在受冲击时，会发生压缩-膨胀现象，在水平方向上胞元有向外扩散的现象。因此在平台区平缓，不会出现平台应力增强现象。胞元胞壁随着冲击压缩而逐渐接触和叠加，压缩应力仍变化平缓。参与变形的胞元数量少且胞元变形幅度小，进而导致应力与吸能量表现弱于辊型双V蜂窝。综上所述，造成两蜂窝冲击响应特性差异的原因主要是辊型双V蜂窝胞元与层级间的负泊松比增强效应。

2.3 辊型蜂窝变形模式与动态接触响应

轮辋反力是林木联合采育机进料辊法兰与液压驱动轴受到的力，如图6（a）。结构接触力是蜂窝结构进料辊与原木接触面间存在的力，可直观反映出原木的受力情况，如图6（b）。辊型双V蜂窝的轮辋反力随着的增大，轮辋反力曲线波动周期逐渐减小，幅值逐渐增大。由Karagiozova等[22-23]的蜂窝材料激波理论解释，即辊型蜂窝受压缩产生应力激波，应力激波在胞元结构层间界面多次反射，造成了轮辋反力曲线波动。而刚性压缩板与轮辋间的产生的强不连续激波与胞元结构层间的简单激波同时传播反射，使得轮辋反力曲线周期与幅值不规则。胞元结构层数少，应力激波反射次数少且受到的减弱效应小，使得曲线波动得到放大。0.5与1.0辊型蜂窝在结构接触力近似的情况下，轮辋反力数值在各阶段均低于2.0辊型蜂窝，证明其具有优异的结构强度与稳定性。由于局部应力超过胞元壁与附翼的弹塑性屈曲极限，导致胞元壁出现坍塌连锁效应，应力激波传播方向改变，使得2.0辊型蜂窝结构接触力曲线在0.4时出现大幅骤降与剧烈波动。辊型六角蜂窝横向参与变形胞元少且变形关联不密切，以至于应力激波反射次数频率高，应力激波传播方向固定。因此辊型六角蜂窝轮辋反力与结构接触力曲线波动频率高，但波动周期与幅度变化较小。随着第一结构层的胞元进入压实，应力激波反射行程缩短，曲线在0.35后波动周期与幅值均明显增大。辊型六角蜂窝的轮辋反力大于辊型双V蜂窝，而结构接触力却大幅小于辊型双V蜂窝。在相同冲击强度需求下，使用辊型六角蜂窝的进料辊比使用辊型双V蜂窝的进料辊，需要整体匹配更高强度的法兰与进料辊液压驱动系统。

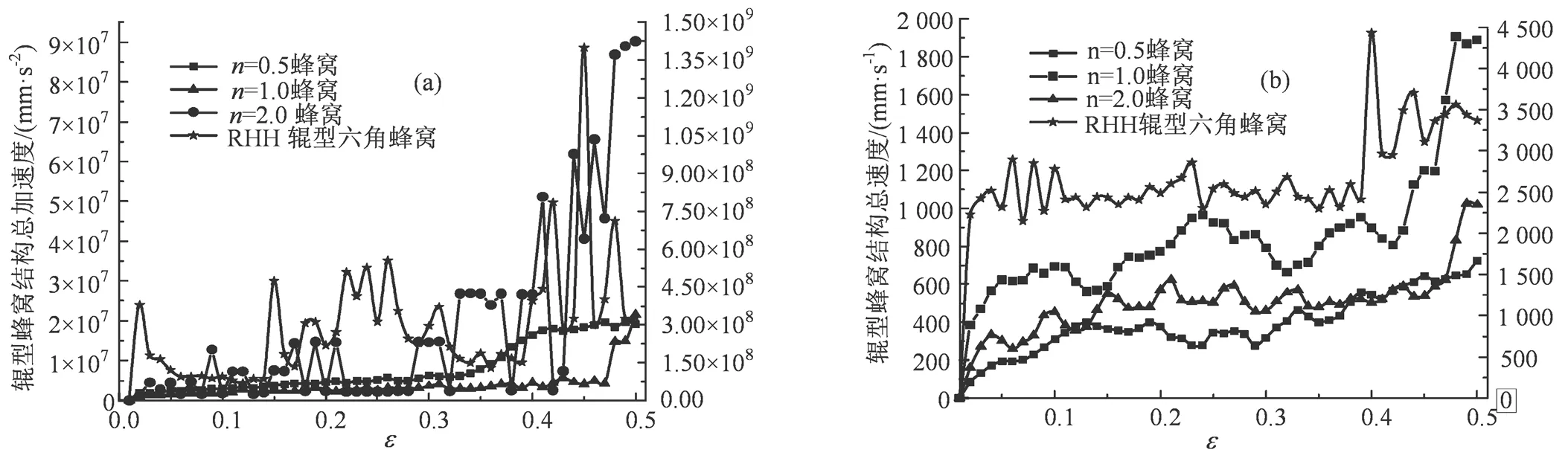
图7 辊型蜂窝总加速度与速度响应曲线

Figure 7 The response curves of roller honeycombs for total acceleration and velocity

图7（a），7（b）分别给出辊型蜂窝的总加速度与总速度的响应曲线。此项参数反映出各辊型蜂窝在低速冲击下的结构稳定性。可以看出，辊型蜂窝受应力激波与胞元弹塑性变形不同步的影响，加速度与速度曲线产生波动。辊型蜂窝总加速度与速度曲线变化受单位胞元变形行为的共同影响。0.5、1.0和2.0蜂窝总胞元数分分别为72、24和8，辊型六角蜂窝规则胞元、完整胞元（不包含外侧不完整胞元）与总胞元数分别为24、36和48。0.5和1.0蜂窝单位胞元速度与加速度数值远低于2.0蜂窝，且0.5蜂窝单胞元数值最小，结构最稳定。因此，辊型双V蜂窝胞元密度越大，总胞元数越多，单位胞元速度与加速度越小且趋势平稳，辊型双V蜂窝结构的结构稳定性越强。辊型六角蜂窝胞元尺寸和胞元数量与1.0蜂窝相似，但结构总加速度与速度远远高于辊型双V蜂窝，曲线受应力激波的影响波动剧烈。在相同冲击条件下，辊型双V蜂窝的结构稳定性远远高于辊型六角蜂窝。辊型六角蜂窝在实际应用中需要匹配更高强度的部件和更多的设计余量为增强结构稳定性。

2.4 辊型蜂窝位移结构效率评价指标

辊型蜂窝位移性能效率数值结果图如图8。文中提出结构效率评估系数，分为位移性能效率与体积性能效率，分别表示辊型蜂窝在单位位移或者单位体积下产生的应力与吸能量，衡量辊型蜂窝的经济-性能间的平衡与效能。位移性能效率对应各性能的参数，分别记为ED-Equivalent stress（ED-E），ED-Normal stress（ED-N），ED-Shear stress（ED-S）与ED-Energy absorption (ED-W）。位移性能效率计算于50%压缩比区间前的辊型蜂窝性能结果最大值与各压缩位移的比值。可以发现各辊型双V蜂窝结构位移性能效率数值接近，即相同厚宽比的辊型蜂窝在单位位移下具有近似的力学性能，进一步验证了辊型蜂窝的等效关系。辊型双V蜂窝位移力学效率变化趋势随增大而减小，吸能量随增大而增加。相同应变下，低的蜂窝参与变形的胞元数量多，负泊松比增强效应更强，应力平台高且长，所以应力表现优异。但单个胞元的塑性变形幅度远小于高的蜂窝，吸能平台较低，吸能量较少。辊型六角蜂窝由于缺少负泊松比增强效应与大尺寸塑性变形胞元，单位位移下的应力与吸能量均低于各辊型双V蜂窝。此外，结合上述的位移性能效率数值变化，可以发现辊型双V蜂窝参数与位移吸能效率数值存在非线性规律。辊型六角蜂窝的壁厚较薄，其体积与0.5蜂窝较为接近并远小于1.0和2.0蜂窝。是辊型双V蜂窝结构的主要参数和等效关系的成立基础变量。根据辊型双V蜂窝结构的等效关系与理论模型，其性能指标与厚宽比有关，可以用的多项式拟合表示。由于与厚宽比直接相关，因此确定为拟合曲线的自变量，辊型双V蜂窝结构的位移效率拟合曲线分别为ED-E、ED-N、ED-S和ED-W：

ED-E()=—0.013 7462+0.014 920—0.185 726 （10）

ED-N()=0.018 9002—0.048 350—0.173 510 （11）

ED-S()=0.009 3332—0.038 000—0.103 667 （12）

ED-W()=278 7.262—240 3.22+336 5.98 （13）

2.5 辊型蜂窝体积结构效率评价指标

位移性能效率对应各性能的参数，分别记为EV-Equivalent stress (EV-E)，EV-Normal stress (EV-N)，EV-Shear stress (EV-S)与EV-Energy absorption (EV-W)，如图9。体积性能效率计算于50%压缩比区间前的辊型蜂窝性能结果最大值与各辊型蜂窝体积的比值。辊型双V蜂窝力学、吸能量分别随的增大而减小、增大的趋势更加明显。而辊型六角蜂窝具有更小的体积，与辊型双V蜂窝的体积性能效率差距缩小，并在EV-S中超过了2.0蜂窝。0.5蜂窝具有最优异的体积力学效率，2.0具有最佳的体积吸能效率，1.0兼顾有最均衡的体积力学与吸能效率特性，而辊型六角蜂窝的体积性能效率较低。相同性能条件或质量要求下，辊型双V蜂窝性能表现与经济性均优于辊型六角蜂窝。为了探究等效辊型蜂窝体积效率的数学规律，得到R=1的拟合曲线EV-E、EV-N、EV-S和EV-W：

EV-E()=—0.260 6672—0.111 000+0.173 510 （14）

EV-N()=0.440 0002—1.420000+4.190 000 （15）

EV-S()=0.813 3332—3.040 000+3.806 667 （16）

EV-W()=53.573 3332—46.360 000+76.416 667（17）

图8 辊型蜂窝位移性能效率数值结果

Figure 8 The displacement-performance efficiency of roller honeycombs

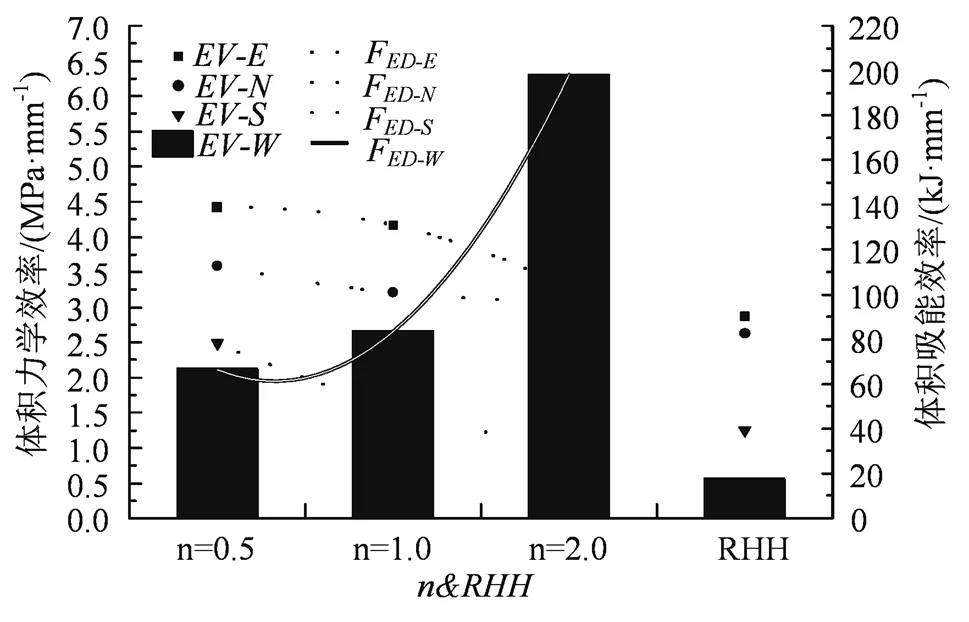
图9 辊型蜂窝体积性能效率数值效果

Figure 9 The volume-performance efficiency of roller honeycombs

3 讨论与结论

（1）提出结构效率评估系数概念，分为位移性能效率与体积性能效率，衡量辊型蜂窝的经济-性能间的平衡与效能。位移性能效率数值验证相同厚宽比的辊型双V蜂窝在单位压缩量下具有近似的力学性能，位移效率和体积效率数值与蜂窝结构参数存在非线性规律并得到拟合表达式，以预测等效关系下辊型蜂窝的力学吸能能力。相同性能条件、位移或质量要求下，辊型双V蜂窝性能表现与经济性均优于辊型六角蜂窝。

（2）辊型双V蜂窝结构得益于负泊松比增强效应，具有几倍于辊型六角蜂窝的力学性能与能量吸收表现、更稳定的力学吸能曲线、更长的弹塑性平台和更晚的压实区间。辊型六角蜂窝受冲击产生压缩-膨胀现象，胞元在水平方向上向外扩散，胞元层级间无负泊松比增强效应、胞元数量少和胞元变形幅度小，进而导致应力与吸能量表现弱于辊型双V蜂窝。辊型双V蜂窝结构受压后产生的负泊松比效应，在增大接触面积的同时，单位面积内的压力和动力冲击都会减少，从而减少原木损伤。

（3）辊型蜂窝压缩过程中的轮辋反力与结构接触力得到了量化。根据数值趋势，辊型蜂窝结构的轮辋反力随着胞元密度的增大，轮辋反力曲线波动周期逐渐减小，幅值逐渐增大。受应力激波反射层面与方向的影响，随胞元密度的减小，辊型蜂窝胞元更易出现坍塌连锁效应，导致结构接触力产生波动与接触力骤降。辊型六角蜂窝轮辋反力与结构接触力曲线波动频率高、波动周期与幅度变化较小，且波动周期与幅值随应变增大而变化剧增。

（4）辊型双V蜂窝总加速度与速度响应相受单个胞元变形行为的共同影响。蜂窝胞元密度越大，胞元数越多，单位胞元速度与加速度越小且趋势平稳，辊型双V蜂窝结构的结构稳定性越强。辊型六角蜂窝结构总加速度与速度远远高于辊型双V蜂窝，曲线波动剧烈。在相同冲击条件下，辊型双V蜂窝的结构稳定性远远高于辊型六角蜂窝。

对于本研究，动态冲击模型可以为辊型双V蜂窝结构的结构设计、关键参数选择策略和预测性能提供新思路与方法。相关的结果与讨论可用于选择符合伐木工况的最佳蜂窝结构，从而减少进料辊与原木的损伤，提高机械化伐木的生产效率。

[1] GERASIMOV Y, SELIVERSTOV A, SYUNEV V. Industrial round-wood damage and operational efficiency losses associated with the maintenance of a single-grip harvester head model: a case study in Russia[J]. Forests, 2012, 3(4): 864-880.

[2] 杨桂娟, 段爱国, 邓伦秀, 等. 不同立地条件下杉木人工林材种结构间伐效应的长期定位研究[J]. 安徽农业大学学报, 2018,45(3): 444-449.

[3] 张春岭, 陈黎卿, 吴荣. 基于离散元法的勺轮式排种器性能仿真分析[J]. 安徽农业大学学报, 2016,43(5): 848-852.

[4] 涂育合, 叶功富, 林照授, 等. 凹叶厚朴树皮产量预测模型的研究[J]. 安徽农业大学学报, 2003, 30 (3): 312-315.

[5] NUUTINEN Y, VÄÄTÄINEN K, ASIKAINEN A, et al. Operational efficiency and damage to sawlogs by feed rollers of the harvester head[J]. Silva Fenn , 2010, 44(1): 121-139.

[6] VAN DER MERWE J P, PULKKI R, ACKERMAN P. Fibre losses during debranching and debarking of Eucalyptus pulp logs using a single-grip harvester[J]. South For : a J For Sci , 2015, 77(4): 309-313.

[7] SVENINGSSON L. Stud damages on Alvestakubb[D], Alnarp: Swedish University of Agricultural Sciences, 2011.

[8] CONNELL M. Log Presentation: Log damage arising from mechanical harvesting or processing[M]. Australia: Forest & Wood Products Research & Development Corporation, Forestry and Forest Products Report No. PN02 2003, 1309.

[9] STRANDGARD M, WALSH D, MITCHELL R. Productivity and cost of whole‑tree harvesting without debarking in a Eucalyptus nitens plantation in Tasmania, Australia[J]. South For : a J For Sci , 2015, 77(3): 173-178.

[10] 卢杰, 杨铁滨, 邸向辉. 基于Pro/ENGINEER的伐木头进料辊设计[J]. 森林工程, 2014,30(6), 30: 59-62.

[11] PRAWOTO Y. Seeing auxetic materials from the mechanics point of view: a structural review on the negative Poisson's ratio[J]. Comput Mater Sci , 2012, 58: 140-153.

[12] MARTIN J, HEYDER-BRUCKNER J J, REMILLAT C, et al. The hexachiral prismatic wingbox concept[J]. Phys Status Solidi B, 2008, 245(3): 570-577.

[13] JIANG Y, LIU Z, MATSUHISA N, et al. Auxetic mechanical metamaterials to enhance sensitivity of stretchable strain sensors[J]. Adv Mater, 2018, 30(12): e1706589.

[14] WANG C Y, ZOU S C, ZHAO W Z, et al. Multi-objective explosion-proof performance optimization of a novel vehicle door with negative Poisson's ratio structure[J]. Struct Multidiscip Optim , 2018, 58(4): 1805-1822.

[15] LARSEN U D, SIGNUND O, BOUWSTA S. Design and fabrication of compliant micromechanisms and structures with negative Poisson's ratio[J]. J Microelectromechanical Syst, 1997, 6(2): 99-106.

[16] ÁLVAREZ ELIPE J C, DÍAZ LANTADA A. Comparative study of auxetic geometries by means of computer-aided design and engineering[J]. Smart Mater Struct, 2012, 21(10): 105004.

[17] KELVINA FLORENCE S J, RENJI K, SUBRAMANIAN K. Modal density of honeycomb sandwich composite cylindrical shells considering transverse shear deformation[J]. Int J Acoust Vib , 2018, 23(1):11241.

[18] BARANOWSKI P, MALACHOWSKI J. Numerical study of selected military vehicle chassis subjected to blast loading in terms of tire strength improving[J]. Bull Pol Acad Sci Tech Sci , 2015, 63(4): 867-878.

[19] 王栋, 王典, 刘晋浩, 等. 林木联合采育机进料辊填充蜂窝结构的力学特性[J]. 东北林业大学学报, 2020, 48(6), 48: 93-99,104.

[20] QIAO J X, CHEN C Q. Impact resistance of uniform and functionally graded auxetic double arrowhead honeycombs[J]. Int J Impact Eng , 2015, 83: 47-58.

[21] BEZAZI A, SCARPA F. Mechanical behaviour of conventional and negative Poisson's ratio thermoplastic polyurethane foams under compressive cyclic loading[J]. Int J Fatigue, 2007, 29(5): 922-930.

[22] KARAGIOZOVA D, ALVES M. Primary and reflected compaction waves in a foam rod due to an axial impact by a small mass[J]. Lat Am J Solids Struct, 2015, 12(5): 905-924.

[23] KARAGIOZOVA D, ALVES M. Compaction of a double-layered metal foam block impacting a rigid wall[J]. Int J Solids Struct , 2014, 51(13): 2424-2438.

Analyses on key techniques and application performance of honeycomb feeding roller for forest combine harvester

QU Yunfei1,2, WANG Dian1,2, ZHU Xuchen1,2

(1. School of Technology, Beijing Forestry University, Beijing 10083;2. Key Laboratory of Forestry Equipment and Automation of State Forestry and Grassland Bureau, Beijing 100083)

Aiming at solving the problem of reducing wood damage in mechanized cutting operation, the Roller Honeycomb Feeding Roller (RHFR) was proposed. Combined with the relevant mathematical formulas, the dynamic impact model of Roller Double V-Wings Honeycomb (RDWH) was derived and verified by the finite element simulation numerical results. The mechanical and energy absorption characteristics, dynamic response, structural stability and structural efficiency of roller honeycomb under low speed impact under logging conditions were studied, and different shaped Roller Hexagonal Honeycomb (RHH) were investigated for reference. The RDWH, benefiting from the Negative Poisson's Ratio enhancement phenomenon in deformation, possessed higher structural efficiency, stronger impact resistance, better structural stability and larger contact area. When the impact of RDWH reached to0.3, all the stress indexes can meet the requirements of cutting conditions under 1 600 kg. This provided an important reference for mechanized application of honeycomb feeding roller and reducing log damage.

forest harvester; feeding roller; agricultural and forestry machinery; damage to logs

S776.3

1672-352X (2021)03-0496-08

10.13610/j.cnki.1672-352x.20210706.010

2021-7-7 10:35:16

[URL] https://kns.cnki.net/kcms/detail/34.1162.S.20210706.1642.020.html

2020-10-20

国家重点研发计划“战略性国际科技创新合作”重点专项（2016YFE0203400）和中央高校基本科研业务费专项资金项目（2016ZCQ08）共同资助。

曲云飞，硕士研究生。E-mail：quyunfei95@bjfu.edu.cn

王典，博士，副教授。E-mail：wangdian@bjfu.edu.cn