模型不确定的空间机器人无力传感器阻抗控制方法
2021-08-13赵良玉
陶 东,张 强,赵良玉
(1. 北京理工大学宇航学院,北京100081;2. 北京控制工程研究所,北京100094)
0 引 言
通过空间机器人在轨对航天器进行装配、维修或燃料加注等服务是国内外航天领域研究的热点之一[1],在轨捕获是实现上述在轨服务的前提和关键环节[2]。目前,国内外对在轨捕获技术的研究还处于围绕合作目标开展太空试验或地面验证试验阶段,如日本ETS-VII卫星和美国轨道快车任务对空间合作目标的在轨捕获验证、加拿大航天局的自主捕获地面实验系统、深圳航天技术中心地面实验系统、美国加州蒙特利海军研究生院的地面实验系统等[3-4]。当空间机器人实施在轨捕获任务时,其机械臂末端执行器和服务对象之间不可避免地发生相遇及碰撞,碰撞产生的接触力可能会损坏空间机器人及服务对象或将二者彼此推开。因此,在轨捕获是一项非常危险且具有很大技术挑战的任务[5-6]。国内外诸多学者研究表明,力位混合控制方法[7-8]和阻抗控制方法[9]可以实现空间机器人与服务对象之间的柔性接触和柔性抓捕[10]。力位混合控制是将任务空间分解为相互正交的接触空间和自由运动空间,通过选择矩阵实现对末端执行器的控制选择,从而完成机器人末端位置控制和力控制[7]。由于在轨捕获时,碰撞接触力会是任意方向,难以实现自由运动空间和接触空间的解耦,为此,本文选用阻抗控制方法实现空间机器人的在轨捕获操作。
阻抗控制方法的核心理念是通过位置与环境作用力的动态关系实现机械臂与环境的交互,达到柔性接触的目的。Moosavian等假设在机器人基座输入力得到精确控制的情况下,针对多臂空间机器人系统设计了一种阻抗控制律,使整个系统在与服务对象接触时表现出期望的柔性行为[11]。文献[12]提出了一种不需要对基座进行精确控制,便可以实现整个服务系统在惯性坐标系下柔性接触的阻抗控制方法。Abiko等将抓捕时的接触力作为末端执行器的干扰力进行处理,提出了一种不依赖抓捕目标任何惯性参数的阻抗控制方法[13]。文献[14]针对非合作目标捕获问题提出了一种PD控制和阻抗控制相结合的方法,使得在基座无论如何运动的情况下,末端执行器都能够表现的像一个质量-弹簧-阻尼系统。Uyama等针对服务系统和服务对象碰撞后出现的非期望接触力及接触后的相对运动问题,提出了一种参考恢复系数来调整阻抗参数的阻抗控制方法[15]。上述阻抗控制方法针对特定的问题或特定的应用场景均达到了比较好的控制效果,但由于需要在末端执行器安装测量接触力的力传感器,因此增加了系统的复杂度和硬件成本,同时降低了系统的控制带宽[16]。
为了克服使用力传感器所带来的不足,一些学者尝试使用估计方法来获取接触力。Yoshikawa等通过空间机械臂末端执行器与抓捕对象的相对速度及接触时的冲击大小关系来估计接触力[17]。文献[18]通过自由飞行空间机器人的运动方程来预测接触力,提出了一种包括多个机械臂、基座和操作对象的多重阻抗控制方法,使包括操作对象在内的整个服务系统表现为柔性行为。Flores-Abad等使用精确逆动力学观测接触力,利用PID控制器实现轨迹跟踪,提出了一种基于干扰观测器的空间对象阻抗控制方法,实现了捕获时的柔性接触[16]。由于上述方法均直接或间接依赖于精确的动力学模型,因此当动力学模型存在不确定时,则可能会出现接触力估计误差过大,导致系统稳定性变差甚至失去稳定的情况发生。考虑到空间机器人在太空中工作时,由于燃料消耗、基座和机械臂动力学耦合、关节摩擦力、电机死区、重力梯度等因素的影响[19],进行精确动力学建模几乎不太可能。因此,在考虑空间机器人动力学模型不确定的情况下进行接触力估计,并进而开展阻抗控制更有现实意义和应用价值。
针对自由漂浮空间机器人在轨捕获中与服务对象的碰撞问题,本文提出了一种考虑模型不确定情况下的无力传感器阻抗控制方法。首先,在建立空间机器人不确定动力学模型基础上,推导了估计接触力与不确定部分的关系;其次,将接触力的估计分为两部分,一部分通过不确定模型进行估计得到,另一部分利用神经网络对模型不确定部分进行辨识得到;最后,将后一部分估计得到的接触力作为前一部分估计所得接触力的补偿,并将补偿后的估计接触力作为空间机器人末端执行器期望位置的反馈,使其表现出类似质量-弹簧-阻尼的特性,最终实现柔性抓捕。
1 空间机器人的运动学和动力学模型
为方便分析且不失一般性,本文基于以下假设建立自由漂浮空间机器人的运动学和动力学模型。
1)空间机器人和服务对象都是刚体,空间机器人的位置和姿态不受控制。
2)忽略重力梯度、太阳风及磁场对空间机器人的影响。
3)已知空间机器人的运动状态和服务对象的运动状态。
1.1 运动学模型
假设空间机器人由卫星基座和n自由度的串联机械臂组成,如图1所示。其中,∑I、∑0、∑c、∑1~∑n和∑T分别为惯性坐标系、基座坐标系、捕捉坐标系、关节1~关节n坐标系和工具坐标系;ri∈R3为连杆i质心的位置矢量;re∈R3为末端执行器的位置矢量;ai∈R3为从关节i指向连杆i质心的位置矢量;bi∈R3为从连杆i质心指向关节i+1的位置矢量;ρi∈R3为关节i的位置矢量;θ∈Rn为关节角向量,即θ=[θ1,…,θn]T,θi为关节i的转动角度;ωi为连杆i的角速度矢量;v0、ω0分别为基座的线速度和角速度矢量;ve、ωe分别为末端执行器的线速度和角速度矢量;zi∈R3为各连杆旋转方向的单位矢量。

图1 空间机器人的多体动力学模型Fig.1 Multi-body dynamics model of space robot
从图1可知,空间机器人机械臂末端的位置矢量为[20]:
(1)
由式(1)求导可得,空间机器人机械臂末端的线速度可表示为:
(2)
空间机器人机械臂末端的角速度可表示为:
(3)
由式(2)和式(3)整理可得,空间机器人末端执行器的线速度和角速度、基座的线速度和角速度、机械臂关节的角速度的关系为:
(4)

1.2 动力学模型
卫星基座受控且机械臂末端受到外力和力矩的空间机器人动力学方程为[8]:
(5)

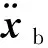
(6)
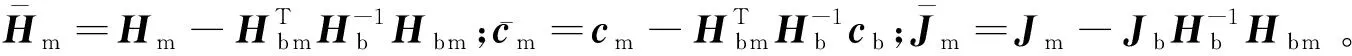
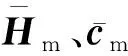
(7)

(8)
(9)
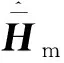
2 力观测器设计
在实际工程中,一些为达到控制目的所必需的信息量要么出于技术限制不能直接获得,要么出于经济、重量、复杂度和带宽等考虑无法直接获得,这就需要通过观测估计的方法来获得这些信息量。在本文中,为了实现空间机器人与服务对象接触时的阻抗控制,需要对空间机械臂抓捕服务对象时的接触力进行估计。为了在空间机器人动力学模型不确定情况下,能够较准确的估计末端执行器与服务对象之间的预期接触力,将接触力估计分为两部分,一部分为利用空间机器人的逆动力学关系,通过不确定动力学模型估计得到的接触力;另一部分为通过神经网络辨识估计得到的接触力。
2.1 不确定模型估计接触力
若空间机器人的精确动力学模型已知,由式(6)可得:
(10)

(11)
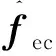
2.2 神经网络辨识估计接触力

(12)
将式(12)减去式(11),可得:
(13)

(14)
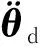
将式(14)代入动力学方程式(6),可得:
(15)
式(15)等号右边第一项包括动力学模型的不确定部分,采用高斯径向基神经网络对该项进行逼近并整理可得:
(16)

理想网络权值可表示为:
(17)
至此,动力学方程不确定项可近似表示为:
(18)
将式(18)代入式(13),可得基于神经网络辨识估计的接触力为:
(19)
3 阻抗控制实现
为了使空间机器人的末端执行器与目标接触时表现为柔性行为,估计接触力与末端执行器的阻抗关系需满足[16]:
(20)

(21)

考虑实际工程情况,位置差值的更新率可写为:
Δ(Δre)≡Δre(t)-Δre(t-T)=
(22)
其中:T为采样周期。
将式(20)代入式(22),可得:
(23)
因此,空间机器人末端执行器的实际参考位置可写为:
rea=red-Δre
(24)
基于观测接触力实现阻抗控制的原理框图如图2所示,观测器估计的接触力作为式(23)的输入,可获得空间机器人末端执行器期望位置与实际参考位置差值;再利用式(24)可获得空间机器人末端执行器的实际参考位置。
4 案例研究
4.1 系统构型及参数
以一个安装平面二连杆机械臂的自由漂浮卫星基座为例来验证本文所提方法的有效性,其构型如图3(a)所示,其参数如表1所示,其中Ii为连杆i的转动惯量。为方便计算,假设每个连杆的质心在连杆的中心点;捕捉坐标系和惯性坐标系的原点在空间机器人基座的中心点。空间机器人的初始状态为:θ0=0,θ1=π/6,θ2=π/6,re=[1.8809, 1.3809]T。

表1 空间机器人参数Table 1 Space robot parameters
用一个如图3(b)所示的虚拟墙来代替抓捕对象。

图3 仿真系统Fig.3 Simulation system
为完成仿真,空间机器人的末端执行器与虚拟墙接触时,虚拟墙对末端执行器产生的接触力采用Hertz model[16]进行计算:
(25)
其中:kc、cc是和两个接触对象的材料属性相关的参数;ζ是碰撞力的方向向量;δ为末端执行器和服务对象抓捕点的距离。
4.2 仿真结果
给定期望轨迹red=[0.02t+1.93, -0.01t+10.4]T,并在x=1.94处,设置一堵虚拟墙,取kc=50000 N/m,cc=1 Ns/m。
其中:P为A和Q的李雅普诺夫方程对称矩阵,φ为高斯径向基函数。
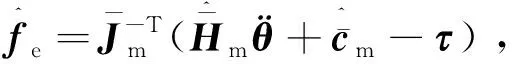


图4 动力学模型精确情况下两种方法阻抗控制效果Fig.4 The impedance control effect of the two methods with dynamic model accurate
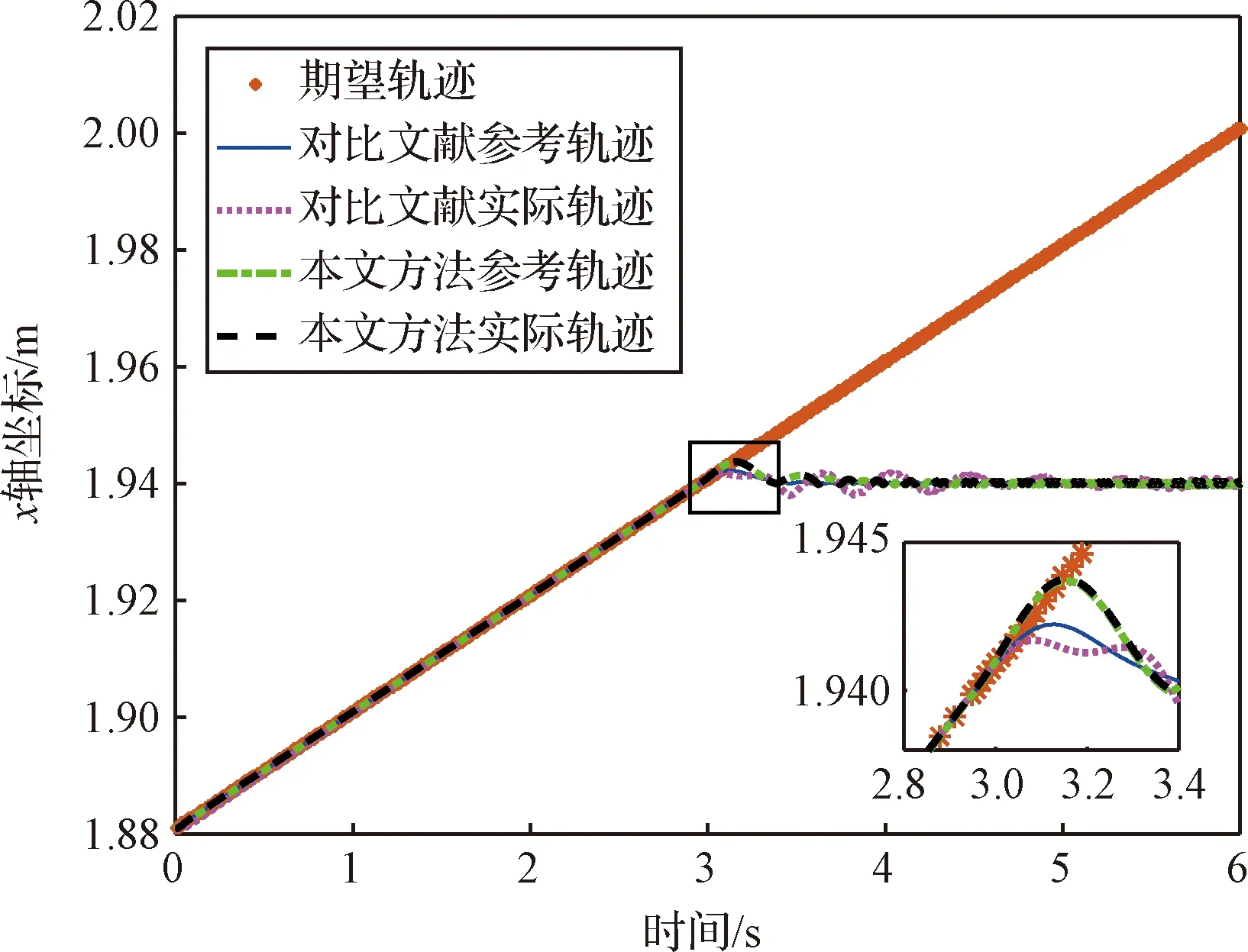
图两种方法阻抗控制效果Fig.5 The impedance control effect of the two methods with
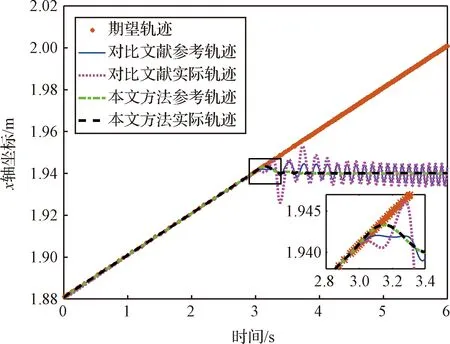
图两种方法阻抗控制效果Fig.6 The impedance control effect of the two methods with
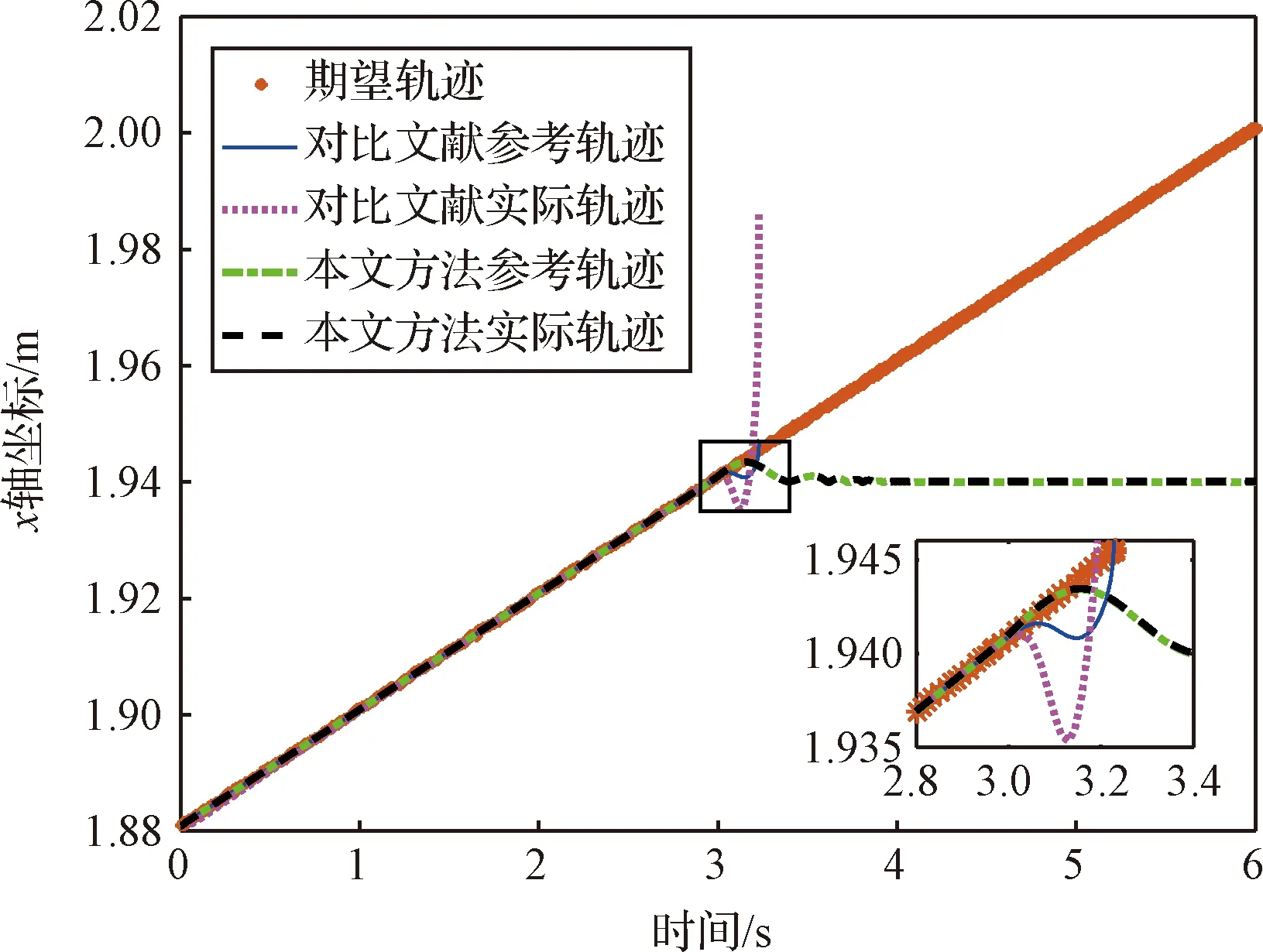
图两种方法阻抗控制效果Fig.7 The impedance control effect of the two methods with

图两种方法阻抗控制效果Fig.8 The impedance control effect of the two methods with
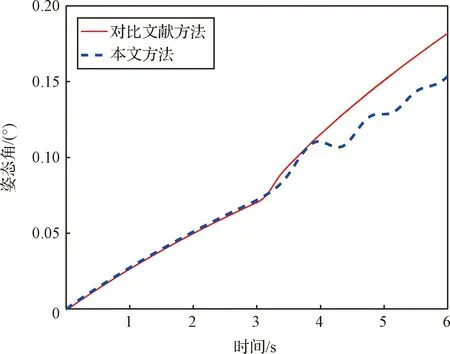
图9 卫星基座姿态角Fig.9 Satellite base attitude angle
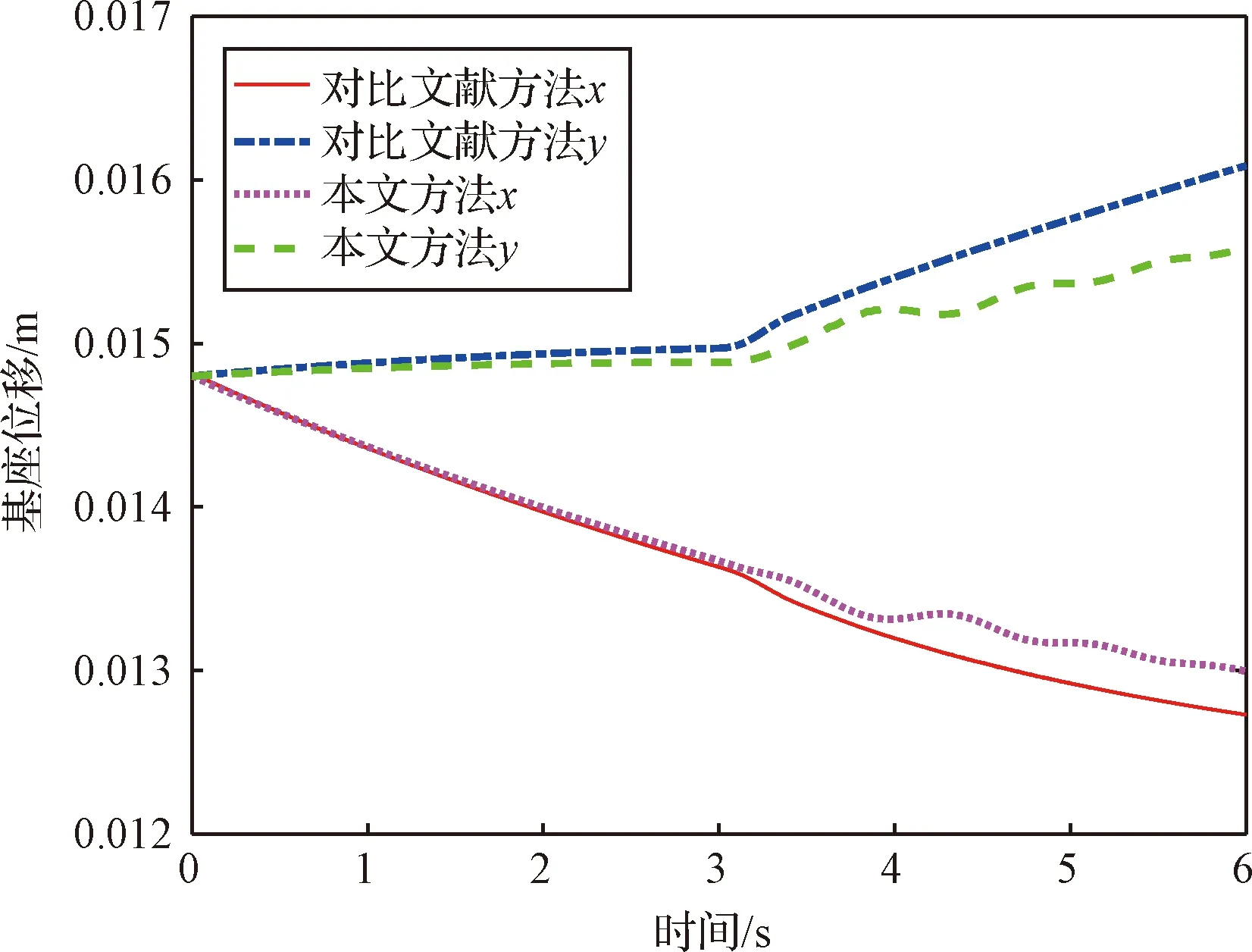
图10 卫星基座位移Fig.10 Displacement of satellite base
由图9和图10可知,本文方法和文献[16]方法的空间机械臂运动对卫星基座均产生了一定的扰动。在空间机器人的末端执行器与虚拟墙接触之前,两种方法对卫星基座姿态和位移的影响较为一致;在末端执行器与虚拟墙接触后,两种方法对卫星基座姿态和位移的影响均有所增大,但本文方法对基座影响的幅度略小于文献[16]方法。
采用本文提出的方法,在空间机器人的动力学参数与其真值相对误差为20%时,末端执行器在x-y平面的轨迹如图11所示。由该图可以看出,空间机器人的末端执行器在与虚拟墙发生碰撞的瞬间,先有一个过冲,再慢慢返回到x=1.94附近,实现了末端执行器与虚拟墙的柔性接触。

图11 空间机器人末端执行器x-y轨迹Fig.11 The x-y trajectory of the end-effector of the space robot
5 结 论
本文针对空间在轨服务中的柔性抓捕需求,提出了一种在动力学模型不确定情况下使用观测器估计接触力并实现阻抗控制的方法。通过将神经网路辨识估计的接触力作为不确定模型估计的接触力的补偿,实现了空间机器人在动力学模型不确定情况下对接触力的有效估计,克服了现有方法在动力学模型不确定时接触力估计误差偏大及导致控制品质降低甚至发散的问题。仿真结果显示,在空间机器人与虚拟墙无接触时,末端执行器能够正常跟踪期望轨迹;在与虚拟墙接触后,末端执行器表现为柔性接触,验证了该方法的有效性。由于本文方法考虑了动力学模型不确定情况和关节摩擦力、电机死区等非线性干扰因素,可有效降低对空间机器人动力学建模精度的要求,具有一定的工程应用价值。
