考虑动态控制分配的空天飞行器再入姿态复合控制设计

董 哲，刘 凯，李旦伟，章吉力

(1. 大连理工大学航空航天学院，大连 116024；2. 沈阳飞机设计研究所，沈阳 110035)

0 引 言

本文的研究对象空天飞行器(Aerospace vehicle, ASV)，是指能够在稠密大气层、临近空间和近地轨道上自由往返、水平起飞并可重复使用的新一代运载器[1-3]。空天飞行器再入飞行阶段具有飞行包线大、动力学特性变化剧烈、横侧向气动耦合显著以及异类执行机构复合任务复杂等特点，给再入姿态控制问题带来了挑战[4-6]。

再入控制方面，传统增益调度控制(Gain scheduling, GS)方法是目前应用最广泛的飞行控制律，在飞行包线内选取若干工作点的线性模型，利用线性系统理论设计控制器[7-9]。非线性动态逆控制(Nonlinear dynamic inversion, NDI)方法使得非线性和线性兼容而无需复杂的增益调度，文献[10]将NDI和PID控制结合，使带有参数摄动的闭环系统具有良好的鲁棒性能。当研究对象的数学模型不够精确时，文献[11]设计了自适应模糊滑模控制器，通过模糊逼近法则对控制器进行了补偿；文献[12]针对X-43飞行器设计了基于Terminal滑模方法的姿态控制器，明显减小高频噪声的同时提升了系统鲁棒性。此外，模型预测控制(Model predictive control, MPC)方法也得到了愈发广泛的应用，该方法在一组未来输入上优化指定的性能指标，以最小化未来输出偏离指定轨迹的误差[13]。文献[14]将其推广到了非线性高性能航空航天系统中，获得了良好的动态轨迹跟踪能力。文献[15]将NDI与约束线性MPC相结合，实现了最优控制并通过状态约束在控制律设计中反映了性能要求。

指标分配方面，空天飞行器再入过程包含大气稀薄、动压小的阶段，需设计一定的分配方法实现RCS和气动舵面的复合控制。非优化分配方法有直接法、链式递增法等；优化分配方法有线性规划法、迭代伪逆法、最小二乘法等[16]。文献[17]提出了一种菊花式链接(Daisy-Chaining)控制分配算法，将飞行器的执行机构按优先级分成若干组，每一级执行器达到饱和后指令便会输入进下一级执行器中。文献[18-20]针对一些中小规模约束的分配问题，提出了连续最小二乘和加权最小二乘分配算法，具有较好的分配精度和较快的运行速度。文献[21]采用二次规划对气动舵面力矩指令问题进行求解，仿真结果表明混合分配方法可有效实现执行冗余机构的高精度分配。目前已有的优化分配方法，其性能指标多考虑分配精度和反作用控制系统燃料消耗，未考虑由于整体闭环控制系统响应速度的需求。

在相关学者研究的基础上，本文针对ASV再入段面临的控制分配问题提出了改进性解决思路。首先，建立了ASV再入姿态动力学模型；然后，从控制精度和工程应用可行性出发，构建了基于ASV动力学模型的模型预测控制器，并在横侧向通道中针对气动耦合问题引入了交叉耦合反馈项，以提高横侧姿控稳定性；同时，本文提出将闭环控制系统响应速度纳入力矩分配优化指标，建立了基于二次规划的按需动态分配算法，使用响应迅速的RCS执行快变化力矩指令，而气动舵面则用于响应慢变化力矩指令，实现了ASV再入段气动舵面和RCS的复合控制分配。

1 空天飞行器姿态动力学模型

考虑再入阶段ASV由RCS和气动舵面共同控制，在文献[22-23]的基础上，可得机体坐标系下的ASV再入段姿态动力学模型为：

(1)

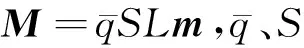
本文采用一阶惯性环节来描述指令到实际偏转的动态过程：

(2)

2 再入姿态控制律设计

空天飞行器再入过程中的异类执行机构有气动舵面和RCS反作用控制系统，因此本文即研究如何使这两种执行机构协同工作来完成ASV再入过程的姿态控制问题。ASV再入段复合控制流程图如图1所示：

图1 ASV再入复合控制流程图Fig.1 Flow chart of ASV reentry compound control

图1中αcmd,βcmd和γV,cmd分别为攻角、侧滑角以及速度滚转角的指令角度；Mcmd为控制律产生的三通道指令力矩；MRCS,cmd为其中分配给RCS的力矩指令；δa,δe和δr分别为副翼舵偏、升降舵偏和方向舵偏。

2.1 纵向预测控制设计

不同于传统控制律，MPC不仅使用当前和过去之间被控量的偏差值，还使用预测模型来预测未来时刻的偏差值，然后使用滚动优化模块使得控制变量与期望值之间的偏差最小，以确定当前时刻最优的控制策略。

首先，基于式(1)中的ASV姿态动力学模型，利用泰勒展开法得到如下纵向离散预测模型[24-26]：

(3)

然后，建立滚动优化函数：

(4)

(5)

(6)

(7)

令∂J/∂U=0，解式(4)表示的优化问题，并将最优控制输入序列的第一个值作为ASV的控制力矩指令：

(8)

Mz,cmd=[1, 0, 0, …, 0]Uopt

(9)

连续控制力矩Mz,cmd输入进RCS执行机构中时，由于其离散的工作特性，常常需要利用PWM脉冲调制将Mz,cmd离散化，进而使RCS响应控制指令。上述MPC控制律工作流程如图2所示。

图2 纵向通道MPC工作流程图Fig.2 Flow chart of longitudinal channel MPC

2.2 横侧向耦合预测控制设计

空天飞行器再入过程横侧向通道气动耦合严重，由姿态动力学知偏航通道耦合有滚转姿态项，同时滚转通道耦合有偏航姿态项。

本文采用耦合控制方案实现横侧向MPC控制律的设计：在滚转通道引入交叉耦合反馈项Kβ·β进行姿控增稳，通过侧滑角β在异通道的反馈，减小因指令突变产生的控制超调，提高被侧滑角β和滚转角γV的稳定性。

利用泰勒展开获得横侧向耦合离散化预测模型：

(10)

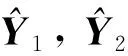
(11)

(12)

(13)

与俯仰通道同理，建立基于离散预测模型的横侧向滚动优化函数如下：

(14)

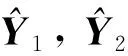
令∂J1/∂U1=0、∂J2/∂U2=0，解式(14)表示的优化问题，并将最优控制输入序列的第一个值作为控制指令：

(15)

(16)

至此，便获得了横侧向通道的耦合预测控制律，其中滚转角的预测向量中包含着交叉耦合系数Kβ。

上述横侧向耦合通道MPC控制律工作流程如图2所示。

图3 横侧向耦合通道MPC工作流程图Fig.3 Flow chart of lateral coupling channel MPC

3 基于二次规划的动态分配律设计

控制分配问题用数学方式描述即

BUr=Mcmd

(17)

式中：B为控制效率矩阵；Mcmd为力矩指令向量；Ur为各执行机构的实际动作量。本文中单通道复合控制的控制效率矩阵和机构实际动作量可表示为：

Ur=[δ,Kr]T

(18)

(19)

式中：δ为δ=[δa,δr,δe]T舵偏向量中的任一舵偏；Kr为Kr=[Kxr,Kyr,Kzr]T向量中的任一元素，表示各通道RCS力矩指令占总力矩指令的占比；Mcmd为Mcmd=[Mx,cmd,My,cmd,Mz,cmd]T向量中的任一元素，表示各通道力矩指令向量；m为m=[mx,my,mz]T向量中的任一元素，表示各通道的力矩系数。

目前采用优化分配算法的文献中多将分配误差和执行消耗作为优化指标[18-21]，未考虑执行机构的工作特性。本文对优化指标进行改进，基于二次规划提出了一种考虑执行机构响应速度的按需动态分配算法：

(20)

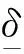
(21)

当需用力矩变化率Γ增大的时候气动舵使用倾向度μ减小，则RCS使用占比增加，用响应快的RCS来执行快速变化的力矩指令；反之，气动舵面使用度增加，以减少RCS能量损耗。需要说明的是上述控制分配模型是针对单通道建立的，且适用于各飞行通道。

4 仿真校验

4.1 仿真参数输入

本节对前文所建立的空天飞行器再入段姿态控制律和控制分配律进行仿真验证与分析。首先，给出仿真所需的部分ASV结构参数与气动参数如表1所示。

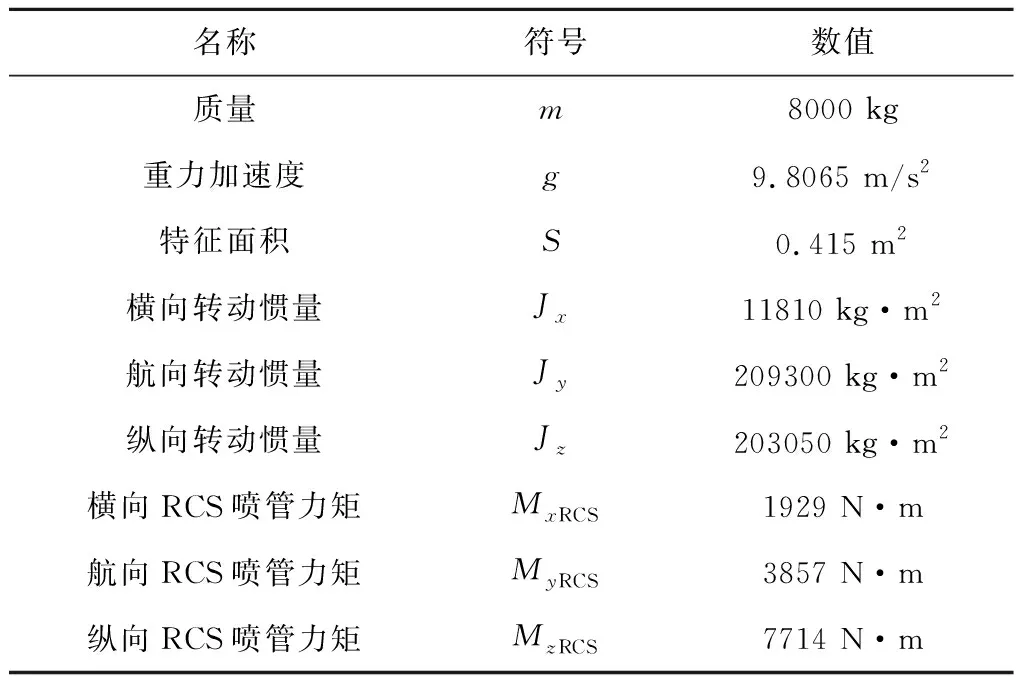
表1 仿真参数Table 1 Description of simulation parameters

4.2 三通道仿真

再入过程复合控制阶段(597～851 s时段)：取αc0=50°,βc=0°,γVc为±45°方波指令；该阶段飞行初始高度为82 km，飞行速度为Ma25。为验证所提方法的鲁棒性，加入气动力矩系数的±40%拉偏，得到下图所示的三通道姿态跟踪仿真曲线，由上到下分别为攻角α、侧滑角β和速度滚转角γVc的响应曲线，其中包括正常气动力矩系数和气动力矩系数拉偏下的响应曲线，以及姿态角指令曲线。

由跟踪曲线可知，本文采用的MPC控制器具有较高的控制精度，同时能够很好地抑制外部干扰，对气动参数的摄动具有较好的鲁棒性。

4.3 横侧向耦合控制对比仿真

空天飞行器再入过程横侧向通道气动耦合严重，本文引入了交叉耦合反馈系数，采取在滚转通道中加入偏航通道状态反馈的方法，以减小指令突变导致的姿态控制振荡，与解耦控制对比仿真结果如图5所示。

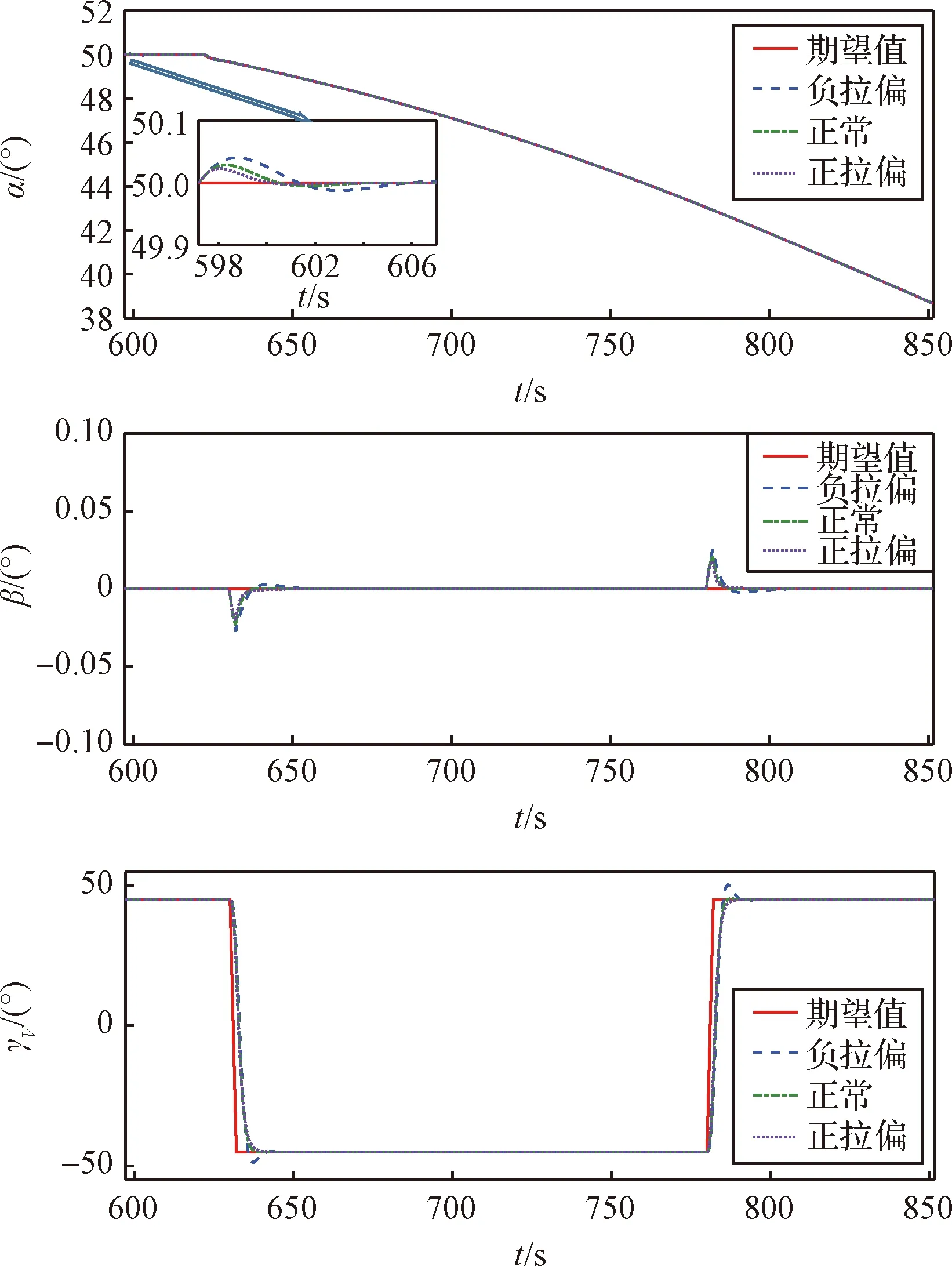
图4 三通道姿态角跟踪曲线Fig.4 Three-channel attitude angle tracking curve

图5 耦合通道姿态角跟踪曲线对比Fig.5 Coupling channel attitude angle tracking curve

由图分析知，与无β反馈相比，有β反馈的耦合控制方法在出现γV指令符号反转的情况下具有较小的超调量，能够快速平稳地完成状态的转变。

4.4 动态控制分配仿真

以俯仰通道为例，利用MATLAB分别求解加权最小二乘控制分配问题和本文改进的基于二次规划的按需动态控制分配问题(20)，得到对应的RCS力矩占比，并用于再入姿态控制仿真。然后通过对比复合控制阶段攻角跟踪误差以及RCS流量消耗来说明按需动态控制分配方法的优势：

图6分配评估曲线中，第一张为采用两种分配方法进行复合姿态控制时的攻角跟踪误差，反应分配方法对控制精度的影响。标称值为图4中的攻角期望值，620 s附近发生突变。按需动态分配方法得到的跟踪误差峰值降低为加权最小二乘分配方法的50%以下；第二张为采用两种分配方法时的复合控制阶段RCS使用比例，按需动态分配方法在该阶段调用RCS的平均比例约为0.2%，相对于不加入响应速度需求的方法的8.3%有了一定程度降低，在实现分配精度的同时有效减少了RCS的燃料消耗。

图6 分配方法评估曲线Fig.6 Allocation method evalution curve

5 结 论

本文针对空天飞行器再入过程异类冗余执行机构的复合控制分配问题，设计了基于二次规划的按需动态分配律，以模型预测控制律输出的指令力矩的变化快慢以及执行机构的响应速度为依据，实现了姿态准确跟踪的同时节省了RCS流量消耗。最后，通过对比仿真分析，验证了该按需动态分配策略的有效性。