制造业可持续供应链网络建模及求解
2021-08-12郭羽含于俊宇刘万军张美琪
郭羽含,于俊宇,刘万军,张 宇,张美琪
(辽宁工程技术大学 软件学院,辽宁 葫芦岛 125105)
0 引言
随着我国可持续发展意识的增强,可持续供应链受到了制造业越来越多的关注。企业如何平衡经济绩效、环境污染和社会责任以保证综合效益最大化成为亟需解决的问题。实施可持续供应链管理可以最大限度地减少供应链对环境的负面影响、提升企业的社会认同度,在为企业带来利润增长的同时,使企业进入可持续发展的良性循环。因此,研究针对制造业可持续供应链的有效决策支持方法变得尤为重要。
制造业供应链一般为由供应商、制造商、分销商和客户组成的多层网络结构,用于描述从原材料采购到向客户交付最终产品的全部过程。涉及到的主要活动包括原材料采购、产品生产和分销、过程中的物流运输[1]。传统供应链网络设计问题的主要目标为对设施的数量[2]、选址[3]以及设施间的产品物流进行决策,在满足客户需求的前提下,追求整个供应链过程中的成本最小化或利润最大化。而可持续供应链指在传统供应链环节中,合理利用自然资源,最小化环境污染并最大化社会责任。近年来,学术界对该领域的研究呈逐年增多的趋势。FAHIMNIA等[4]综述了超过1 000项在可持续供应链管理领域发表的研究,但较有影响力的研究大部分为概念模型和案例分析,而以有效算法优化复杂可持续供应链方面的论文仍然较少;ESKAN-DARPOUR等[5]综述了供应链网络设计领域的87篇论文,涵盖了考虑经济、环境和社会侧指标的数学模型,多数研究只关注碳排放和成本指标,而其他可持续指标则较少出现在供应链优化的研究中,且现有研究中的指标与企业和社会实际关注的指标间仍有一定距离。绿色供应链CITI(corporate information transparency index)指数是全球首个基于品牌在华供应链环境管理表现的量化评价体系,由公众环境研究中心(Institute of Public and Environmental affairs, IPE)和自然资源保护协会(Natural Resources Defense Council, NRDC)合作开发,通过政府监管、在线监测、企业披露等方式获取公开数据,对企业的供应链可持续指数进行动态评价。目前,CITI指数涉及14个行业,收录31省、338地级市政府发布的环境质量、环境排放和污染源监管记录,以及企业基于相关法规和企业社会责任强制或自愿披露的污染数据。该评价体系对企业提升制造业供应链的可持续表现具有显著指导作用。因此,研究基于CITI指标的可持续供应链网络设计对制造业企业的决策辅助具有重要意义。
另外,由于传统供应链网络设计问题已被证明为NP难问题,即使仅考虑单一的经济指标,对于大型算例也很难在可接受时间内获得高质量解,而增加环境和社会侧指标则会显著增大模型的复杂性,从而进一步提高求解难度。因此,精确算法只能解决较小规模的算例[6],高效求解大规模算例成为一个严峻的挑战。文献[7]分析了220篇论文中介绍的优化算法,提出本领域5个未来研究方向,其中之一即是探索高效优化算法,以求解复杂准确的可持续供应链模型。为了更准确全面地将可持续指标纳入制造业供应链网络设计问题模型并解决文献中研究的不足,本文在前期研究[8]和实地调研的基础上,将绿色供应链CITI指数纳入可持续供应链模型中,与污染物排放和转移(Pollutant Release and Transfer Register, PRTR)数据、企业环境表现数据以环境侧的碳排放、废气排放、废水排放和固体废物排放,社会侧的企业事故数和超标整改数的形式,同时结合制造商和分销商落户于当地产生的就业岗位数量以及传统经济侧指标,作为可持续供应链三重底线指标,提出了一个多层次、多产品类型和多能源模式的混合整数线性模型,其中包含4种二进制离散决策变量和4种整型离散决策变量,并对各指标进行了去量纲处理。为更好地平衡求解质量和求解时间,高效求解上述模型,本文提出一种基于多叉树的自适应进化算法。算法采用多叉树编码描述二进制离散决策变量,使用单纯随机法、轮盘赌法和锦标赛法生成变量的初始取值。再以针对本模型设计的剪枝重组和节点置换算子实现了解的迭代寻优,并以单纯形法确定整型离散决策变量的最优取值。此外,算法使用了多种自适应机制以更好地平衡对解空间的搜索深度和搜索广度,并通过基于真实数据的大量实验对模型和算法的有效性进行了验证。
本研究的主要贡献包含以下4点:
(1)将绿色供应链CITI指数纳入可持续供应链模型中,针对经济、环境和社会侧,融入PRTR数据和企业环境表现数据,提出了制造业可持续供应链的综合优化指标。
(2)为可持续供应链构建了一个新的多层次、多产品类型、多能源模式的混合整数线性模型,并提出了多个优化目标的去量纲整合方式及权重设置方法。
(3)提出一种基于多叉树的自适应进化算法以高效求解大型算例,为制造业企业的可持续供应链决策提供辅助。
(4)基于真实企业数据进行了大量的实验,证明了模型和算法的有效性,并据此为制造业企业的可持续改造提出了建议。
1 相关研究
本研究涉及可持续供应链领域的两个主要研究方面:数学模型的构建和求解算法的设计。
(1)数学模型的构建 多数研究集中于单个流程的改进,如设施选址[9-12]或绿色制造[13]。较具代表性的研究如DAI等[14]和牟能冶等[15]将可持续发展的三重底线引入了供应商评估和选择决策中。相对于经济侧相关指标的研究,涉及环境和社会侧指标的文献数量仍然偏少。其中,杨玉香等[16]、李辉等[17]、张李浩等[18]、陈玲丽等[19]均对如何平衡供应链成本和碳排放量进行了研究;张广胜等[20]研究了基于多层物流服务的供应链外部能力供给价格的风险;姜林等[21]研究了公平关切行为对竞争供应链最优决策的影响,构建了由两个竞争制造商、一个零售商组成的供应链模型;于艳娜等[22]研究了需求扰动对零售商竞争下双渠道信息产品供应链的影响,构建了零售商竞争的双渠道信息产品供应链扰动决策模型;张云丰等[23]建立了第三方物流服务商参与的三级时滞易变质品供应链协调模型;王哲等[24]研究了政府规制对双责任双渠道供应链的影响问题,构建了由政府、制造商、分销商以及回收处理商组成的三阶段博弈决策模型;刘志等[25]研究了政府基金政策对供应链最优产品设计决策、生产决策及利润的影响;刘灿等[26]构建了集中式决策与分散式决策下的供应链理论模型;宋寒等[27]建立了碳排放约束下的供应链交易模型,研究了供应链企业间剩余碳排放配额共享机制;潘国强等[28]针对多客户多供应商及多产品城际供应链网络中的供应商和物流路径选择问题,对城际综合运输网络提出一种三阶段路径结构数学模型;胡强等[29]、陈胜利等[30]和郭海峰[31]对逆向物流和闭环供应链进行了研究;文献[32-35]则针对更为具体的案例进行了分析以弥补通用模型中的空白,如关志民等[35]研究了消费者感知偏差对制造商绿色研发投入的影响。然而,多数研究仍将优化重点置于经济绩效相关指标上,其他可持续指标的影响力则相对较小。由表1可以看出,在数学模型方面,多数研究仅针对经济侧或针对经济和环境两侧(分别为16篇和18篇),考虑经济侧、环境侧和社会侧3方面建模的文献则相对较少(6篇)。此外,对可持续指标考虑相对全面的研究一般仅针对选址决策或运输数量决策其中之一,而在完整考虑从采购到生产、分销及其运输过程的相关研究中,绝大多数模型只针对一个特定的环境侧指标,并不能较为全面的考虑可持续供应链的三重底线。

表1 文献模型总结
(2)求解算法的设计 供应链网络设计是组合优化领域里较难求解的问题,对于小规模算例,可以采用分支定界等精确算法来解决[36-37],如WANG等[38]和BOONSOTHONSATIT等[39]将CPLEX用于供应链伙伴选择问题;ALLAOUI等[8]设计了一种基于两阶段混合多目标决策方法的可持续农业食品供应链,并提供了一种求帕累托解的精确算法;SLIMANI等[40]提出一个具有一个零售商和一个供应商的两级供应链的博弈理论模型;李进等[41]设计了一种基于必要性测度的模糊求解算法。随着制造业的模块化和供应链的全球化,候选伙伴的数量大幅增加,对于大型算例,最优化算法无法在可接受时间内求解,因此启发式或元启发式方法被用于在合理的计算时间内产生近似最优解。KANNAN等[42]使用了遗传算法求解循环绿色供应链模型;ROGHANIAN等[43]使用遗传算法优化了逆向物流网络;JIANG等[44]利用遗传算法求解了设施选址问题;KANNAN等[45]结合遗传算法和粒子群算法优化了闭环供应链;JAMSHIDI等[46]提出一个考虑成本和环境因素的多目标优化模型,并设计了一种文化基因算法进行求解;GOVINDAN等[47]通过整合供应链网络设计和订单分配,提出一个多目标优化模型,并设计了一种基于变临域搜索的混合算法;CHAN等[48]提出一种结合层次分析法与遗传算法的复合方法,以评估和选择协作供应链中的最佳解决方案;张明伟等[49]提出结合蚁群算法的混合粒子群算法;景熠等[50]设计了双倍体自适应遗传算法,用于优化一个三阶段闭环供应链系统;杨传明[51]提出一种改良模拟退火遗传混合智能算法对多参数多产品供应链碳足迹模型进行了优化;RAHIMI等[52]设计了一种考虑多种不确定性来源的带数量折扣的随机规避风险可持续供应链,提供了一种求帕累托解的方法,并指出采用元启发式算法对三重底线模型求解是当前研究空白。由表2可以看出,在求解方法方面,现存研究主要分为两种形式:①基于案例进行分析的形式(24篇);②使用算法进行求解的形式(18篇),其中使用精确算法、近似算法对模型进行求解的文献较少(分别为3篇和4篇),采用启发式算法对模型进行求解的文献较多(12篇)。尽管使用启发式算法可以显著降低搜索过程的计算复杂度,但由于种群多样性在收敛到局部最优后显著降低,算法的求解质量与精确算法相比还有一定的距离。此外,由于可持续供应链问题的约束较多,启发式算法极易产生低质量解和不可行解,而对不可行解的修复需要耗费大量计算时间,导致求解时间长、求解大算例质量差等问题。因此,快速、有效地求解大规模算例仍是目前研究的难点。
综上所述,为可持续供应链构建具有现实意义的考虑三重底线的模型,并提出快速、有效地求解算法具有重要意义。为此,本文在综合现有研究的基础上,将绿色供应链CITI指数纳入可持续供应链模型中,并融入PRTR数据和企业环境表现数据以构建一个更为全面的三重底线模型,并提出一种可以高效求解大型算例的自适应进化算法。本文所构建模型与现存研究相比,可持续指标更为全面、评价体系更贴近实际应用。由于CITI指数通过GHG(greenhouse gas)排放因子实现了多种排放指标的整合并确定了多指标的相关权重,配合本文的去量纲方法,既可以进行多目标优化生成帕累托曲线,也可以进行单目标整合优化便利企业进行决策。

表2 文献方法总结
2 数学模型
2.1问题描述
本研究考虑一个由供应商、制造商、分销商和客户组成的四级制造业可持续供应链网络。其中,采购自供应商的原材料需运输至相应的制造商,由制造商生产为产品后,将产品运输至相应的分销商,继而由分销商按照订单需求将商品运输至客户。该网络设计中涉及的指标涵盖经济侧、环境侧和社会侧3方面:经济侧指标包括原材料采购成本、产品生产成本、原材料和产品运输成本以及制造商和分销商的固定运营成本;环境侧指标包括原材料运输至制造商产生碳排放、制造商产品制造产生碳排放、废气排放、废水排放和固体废物排放、产品运输至分销商产生碳排放、分销商将产品运输至客户产生碳排放;社会侧指标为制造商和分销商落户于当地产生的就业岗位数量和企业事故数以及超标整改数。同时,为制造商和分销商设置建厂、关停两种状态,并考虑多种产品种类、能源模式,其中能源模式包括固体燃料(无烟煤、烟煤、褐煤)、液体燃料(原油、燃料油、柴油、煤油、液化石油气)、天然气和电力。
本研究基于以下条件假设:
(1)由于供应商所在地区、规模、采购能力、合作关系不同,导致各供应商的采购成本不同。
(2)由于不同制造商使用能源类型、生产能力不同,制造商生产同一类型产品的生产成本、碳排放、废气排放、废水排放以及固体废排放亦不同。
(3)由于不同制造商或分销商的规模、所在地区不同,导致制造商或分销商建厂、关停的成本不同。
(4)由于不同制造商或分销商所在区域的劳动力成本及市场不同,导致制造商或分销商提供的就业岗位数量不同。
(5)由于不同制造商或分销商的企业安全管理制度和监管制度不同,导致制造商或分销商企业事故数以及超标整改数不同。
(6)由于各供应商到各制造商、各制造商到各分销商、各分销商到各客户的距离不同,导致其运输成本和碳排放不同。
本研究针对的可持续供应链网络结构如图1所示。
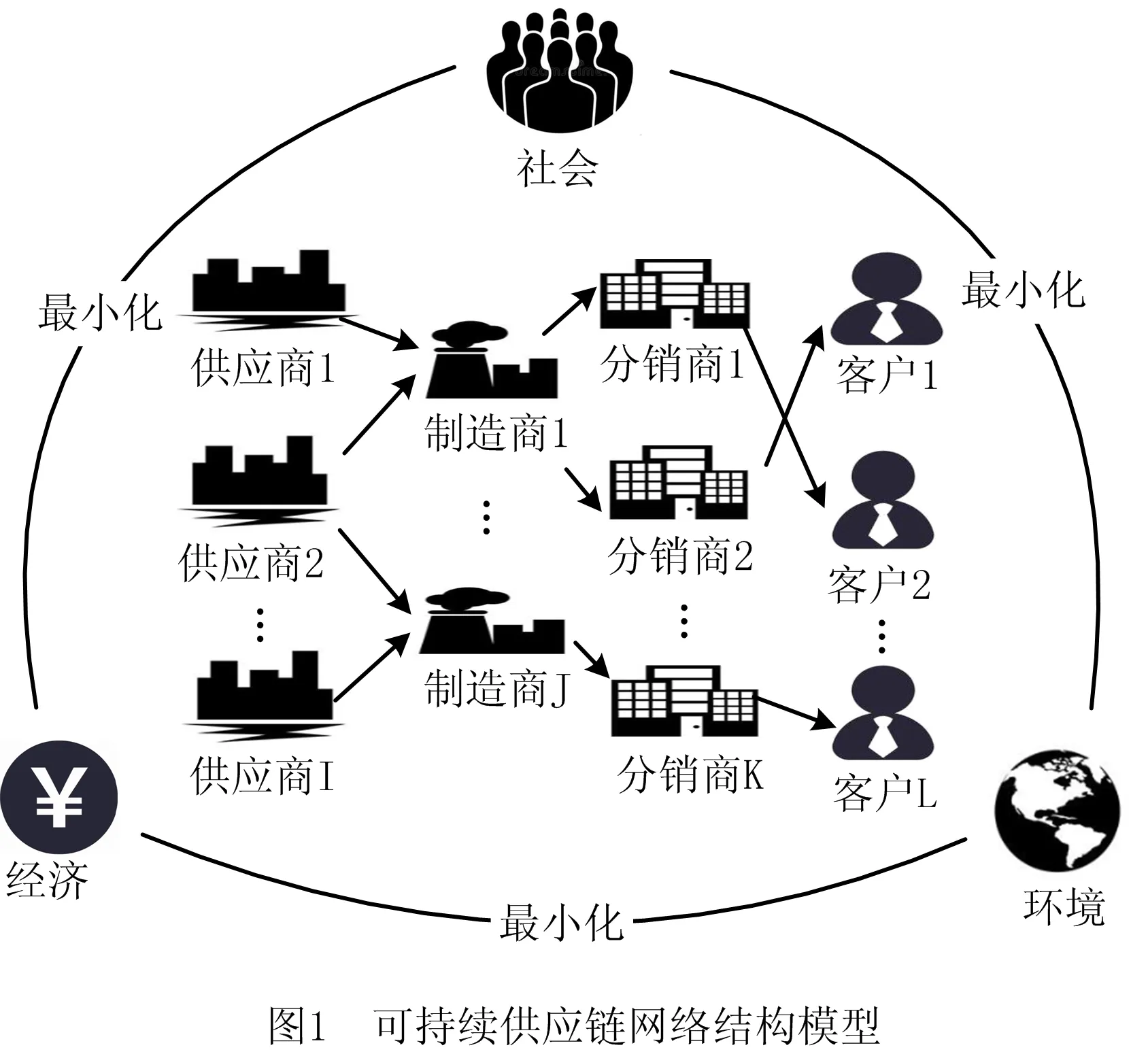
2.2 指标描述
(1)成本
供应商的采购成本由供应商提供;制造商在生产产品过程中的生产成本由制造商提供;制造商或分销商的建厂、关停成本由制造商或分销商结合规模和所在地区预估;供应商、制造商、分销商在运输过程中产生的成本基于历史运输成本计算。
(2)碳排放
制造商在生产产品过程中产生的碳排放主要源于能源消耗,在运输过程中产生的碳排放主要源于运输工具的能源消耗,每消耗一单位能源产生的碳排放量为该能源的GHG排放因子与该单位能源消耗量的乘积。
(3)废气排放
制造商在生产产品过程中产生的废气排放为二氧化硫、氮氧化物、挥发性有机物、烟尘、粉尘等物质的总排放。可根据生产时工厂各废气排放口运行时间和排放速率的乘积累加和计算得到。
(4)废水排放
制造商在生产产品过程中产生的废水排放为工厂各废水排放口在生产产品过程中的废水总排放。可根据生产时工厂各废水排放口运行时间和排放速率的乘积累加和计算得到。
(5)固体废物排放
制造商在生产产品过程中产生的固体废物排放包括一般工业固体废物排放和危险废物排放。
(6)就业岗位数
制造商或分销商在落户地产生的就业岗位总数。
(7)企业事故数
制造商或分销商从建厂至今发生的事故总数。
(8)超标整改数
制造商或分销商从建厂至今进行的碳排放、废气排放、废水排放和固体废物排放超标整改总数。
(9)指标权重
环境侧中碳排放、废气排放、废水排放和固体废物排放对应的权重依据绿色供应链CITI指数的《CITI评价指南6.0》确定。社会侧中就业岗位数量和企业事故数以及超标整改数对应的权重依据绿色供应链CITI指数的《CITI评价指南6.0》和文献[53]确定。经济侧、环境侧和社会侧三者对应的权重依据文献[53]和文献[54]确定。
2.3 目标函数和决策变量
以有向图GV,E表示一个四级可持续供应链网络,其中顶点集V包含四个子集,分别为:供应商候选集I={is},s=1,2,…,ni,其中ni为供应商集合中的供应商个数;制造商候选集J={jt},t=1,2,…,nj,其中nj为制造商集合中的制造商个数;分销商候选集K={kd},d=1,2,…,nk,其中nk为分销商集合中的分销商个数;客户集L={lc},c=1,2,…,nl,其中nl为客户集合中的客户个数。综上,V=I∪J∪K∪L,集合中的每个顶点v为上述类型之一的候选节点,节点vi和vj之间的物流数量以边(vi,vj)∈E的权重表示。根据供应链的定义,只有相邻层中的节点可以相互连接,即is与jt、jt与kd、kd与lc。可持续供应链网络中产品种类集合M={ma},a=1,2,…,nm,其中nm为产品种类个数。能源类型集合E={ea},a=1,2,…,ne,其中ne为能源类型个数。
优化目标为从GV,E的相应层中选择适当数量的is、jt和kd,以满足每个lc的订单,同时在经济、环境、社会侧总体达到最优,同时根据生产能力、仓储能力和连续性限制确定每条边(vi,vj)的权重值。
数学模型中的决策变量和常数如表3和表4所示。

表3 可持续供应链决策变量

续表3

表4 可持续供应链常量

续表4
式(1)~式(3)给出了模型经济侧、环境侧、社会侧的3个目标函数。为求得三个目标函数的综合最优值,以向企业提供更直观的决策辅助,本研究提出了一种目标函数整合方法。在可持续供应链的多指标评价体系中,由于经济侧、环境侧、社会侧各评价指标的性质不同,通常具有不同的量纲和数量级。当各指标间的水平相差很大时,如果直接用原始指标值进行分析,会突出数值较高的指标在决策中的作用,相对削弱数值水平较低指标的作用,导致目标函数中经济侧、环境侧、社会侧各指标在优化时显著不均衡,不同算例的指标值甚至可能相差几个数量级。因此,为了保证结果的应用性和可靠性,本研究采用标准化方法将经济侧、环境侧、社会侧各指标值运用比例变换进行去量纲操作,将各指标值转换为无量纲化指标测评值,即使各指标值均处于同数量级。经过处理的各指标值可以使用更直观的权重值进行整合而无需再考虑原数据量纲带来的影响。本文采用线性标准化方法中的极大化方法,根据线性极大化标准化公式进行缩放变换使各指标值落入特定区间。具体的计算方式为通过计算各指标的上界值,如成本上界Maxcost、碳排放量上界Maxemission、废气排放量上界Maxwaste、废水排放量上界Maxwater、固体废物排放量上界Maxsolid、创造就业数量倒数上界Maxwork、企业事故数上界Maxea、超标整改数上界Maxer,将各个指标值除以各指标上界值使其值域标准化至[0,1]区间,进而实现各目标函数的整合。以成本为例,具体上界计算方法为:在每层的所有备选节点中选择成本最高节点,并将上层订单全部分配给该节点,依次建立供应链从而计算得到总成本即为Maxcost。以上其他上界的计算方法与之类似。
(CODkeodke+CMDkeIODke+CFDkefdke)+
(1)
Maxsolid));
(2)
(ERTjIOTje-ERTjftje))/Maxer))。
(3)
目标函数(1)将经济侧的采购成本、生产成本、运输成本和运营成本的和与Maxcost之比最小化。目标函数(2)将环境侧的碳排放量与Maxemission之比、废气排放量与Maxwaste之比、废水排放量与Maxwater之比和固体废物排放量与Maxsolid之比的和最小化。目标函数(3)将社会侧的创造就业数量的倒数与Maxwork之比、企业事故数与Maxea之比和超标整改数与Maxer之比的和最小化。三个目标函数通过重要性系数a、b、c合并为一个最小化目标函数。
在综合权重的基础上,将多目标规划模型转化为单目标规划模型,如式(4)所示:
Obj=min(a×obj1+b×obj2+c×obj3)
(4)
2.4 约束条件
数学模型的约束条件如下:
(5)
(6)
(7)
(8)
(9)
(m∈M,j∈J,e∈E);
(10)
(m∈M,j∈J,e∈E);
(11)
(m∈M,j∈J,e∈E);
(12)
(m∈M,k∈K,e∈E));
(13)
(m∈M,k∈K,e∈E);
(14)
otje+ftje≤1(j∈J,e∈E);
(15)
odke+fdke≤1(k∈K,e∈E);
(16)
otje+IOTje≤1(j∈J,e∈E);
(17)
odke+IODke≤1(k∈K,e∈E);
(18)
IOTje-ftje≥0(j∈J,e∈E);
(19)
IODke-fdke≥0(k∈K,e∈E);
(20)
otje,IOTje,ftje∈{0,1}(j∈J,e∈E);
(21)
odke,IODke,fdke∈{0,1}(k∈K,e∈E);
(22)
astijm≥0(i∈I,j∈J,m∈M);
(23)
atdjkm≥0(j∈J,k∈K,m∈M);
(24)
adcklm≥0(k∈K,l∈L,m∈M);
(25)
appjem≥0(j∈J,e∈E,m∈M);
(26)
dkl,djk,dij>0(j∈J,i∈I,k∈K,l∈L)。
(27)
其中式(5)为客户需求约束;式(6)为供应商最大供应能力约束;式(7)~式(8)为制造商生产产品的数量约束;式(9)为制造商生产产品时碳排放约束;式(10)~式(14)为制造商和分销商建厂、关停工厂的约束;式(15)~式(20)为制造商和分销商建厂、关停的连续性约束;式(21)~式(22)为制造商和分销商状态约束;式(23)~式(27)为整数约束。
3 基于多叉树的自适应进化算法
传统供应链网络设计问题已被证明为NP难问题,即使仅考虑单一的经济指标,对于大型算例也很难在可接受时间内获得高质量解,而增加环境和社会侧指标则会显著增大模型的复杂性,从而进一步提高求解难度。本文所构建的三重底线可持续供应链模型包含4种二进制离散决策变量和4种整型离散决策变量,是一个典型的混合整数线性模型,其中的二进制离散变量为选址决策,整型离散决策变量为数量决策。根据可持续供应链问题的特性,数量决策依赖于选址决策,只有被选择的厂商才可以进行生产和运输。故可以认定选址决策为首要决策目标,数量决策需在选址决策后才可确定。因此,较为高效的搜索方式为针对二进制离散变量构建首层解空间,并在此解空间的每个节点(即一种选址决策结果)上附加第二层针对整型离散决策变量的解空间。基于上述考虑,本研究提出了一种基于多叉树的自适应进化算法。算法以一棵多叉树描述首层解空间的节点,即选址问题的一种决策结果,其中供应链的每层选址决策映射为多叉树每层的节点选择,并将各层间的供应量关系映射为多叉树各层节点间的权重。而对于第二层解空间最优节点的搜索,即整型离散决策变量的取值,则使用单纯形法完成。由于单纯形法求解连续变量的难度低于求解离散变量,为了进一步提升算法效率,将模型中的整型离散变量松弛为连续变量进行求解。基于上述设计,算法初始构建了基于多叉树的解森林,以对首层解空间的多个节点进行同时搜索,再通过对初始解森林进行迭代进化以在首层解空间搜索最优解。此外,算法设计了多种自适应机制,以动态改变定点剪枝重组和随机节点置换的概率和位置,以保持解森林的多样性并克服解森林的早熟现象。具体流程如图2和伪代码1所示。

伪代码1模型求解算法流程。
输入:定点剪枝重组率Pc、随机节点置换率Pm,解森林规模populationSize,最大迭代次数maxGenergation;
输出:最优解best。
begin
生成初始解森林
k=0
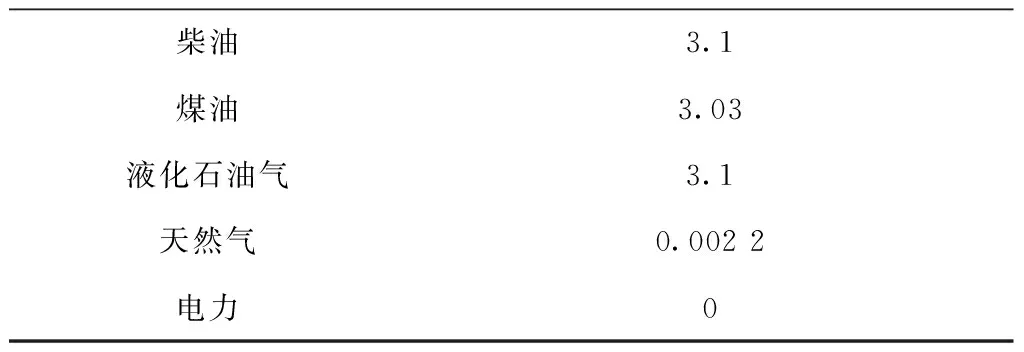
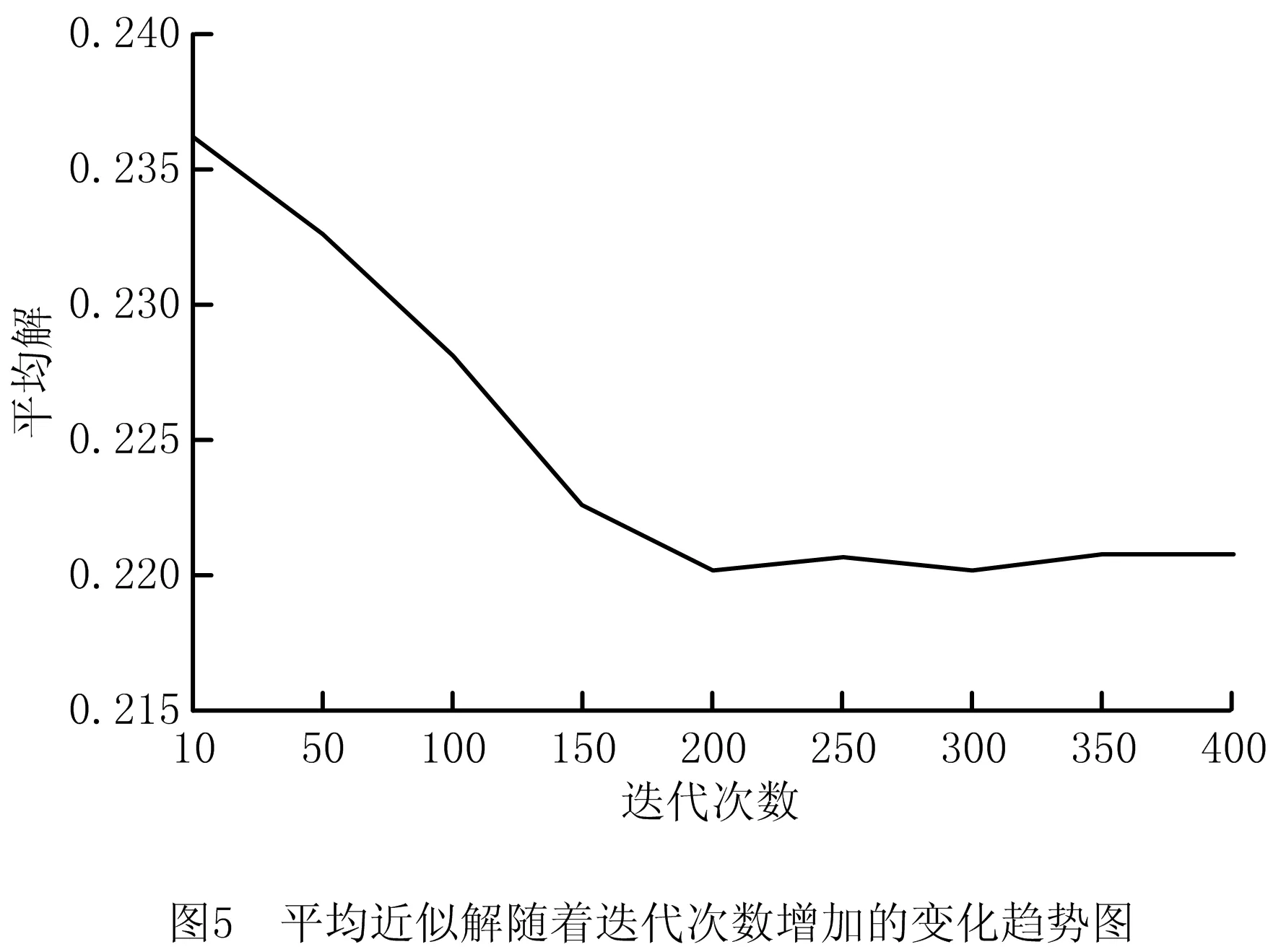
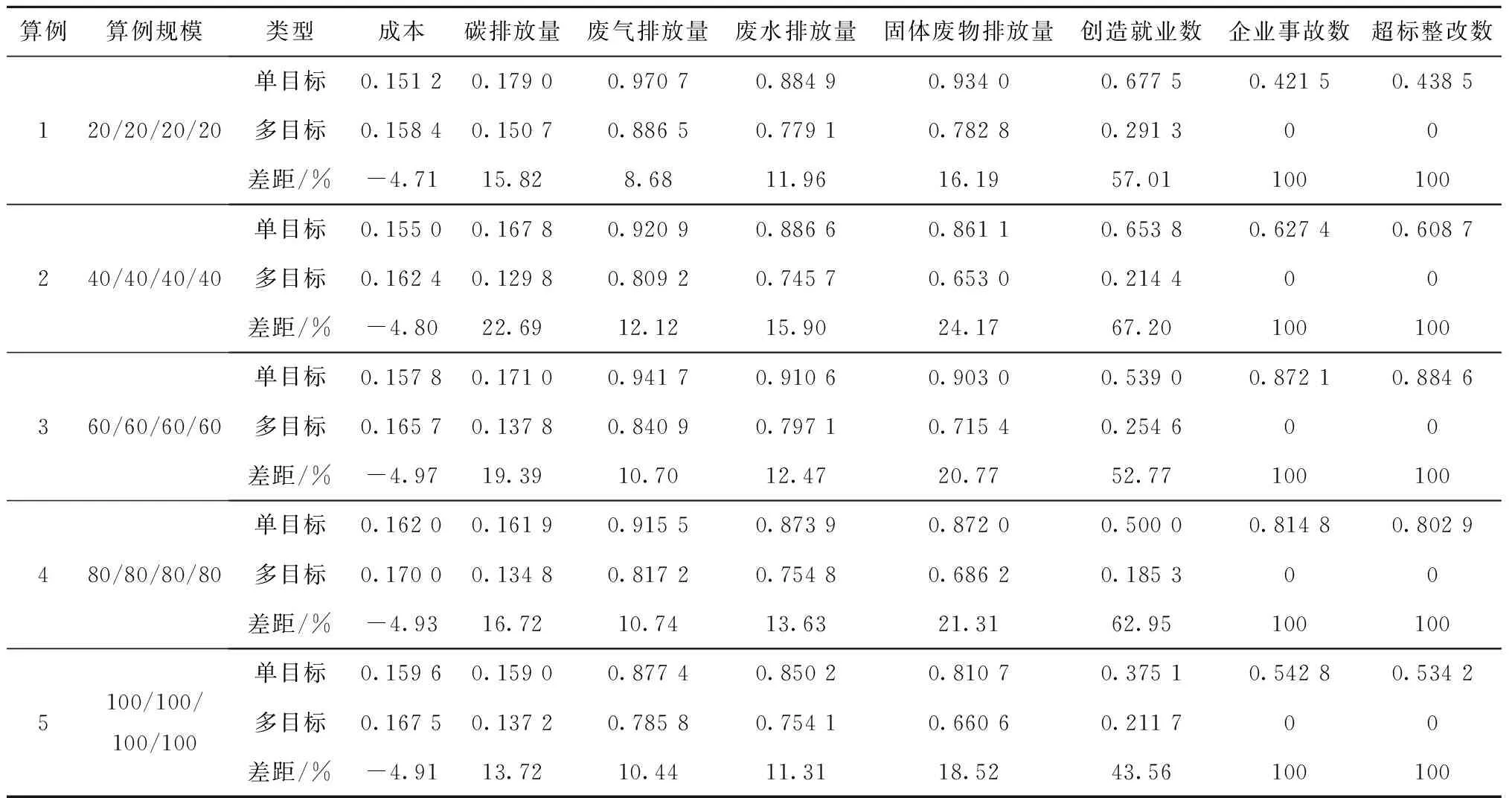
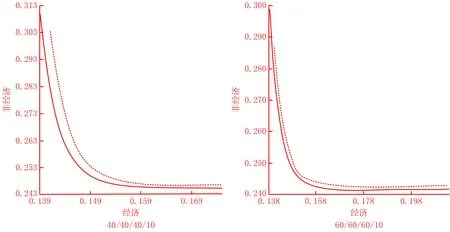
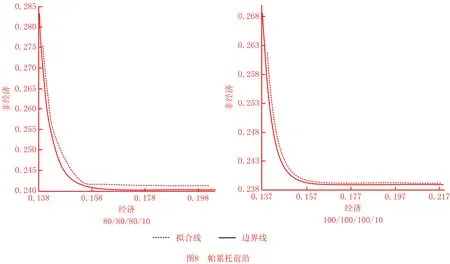
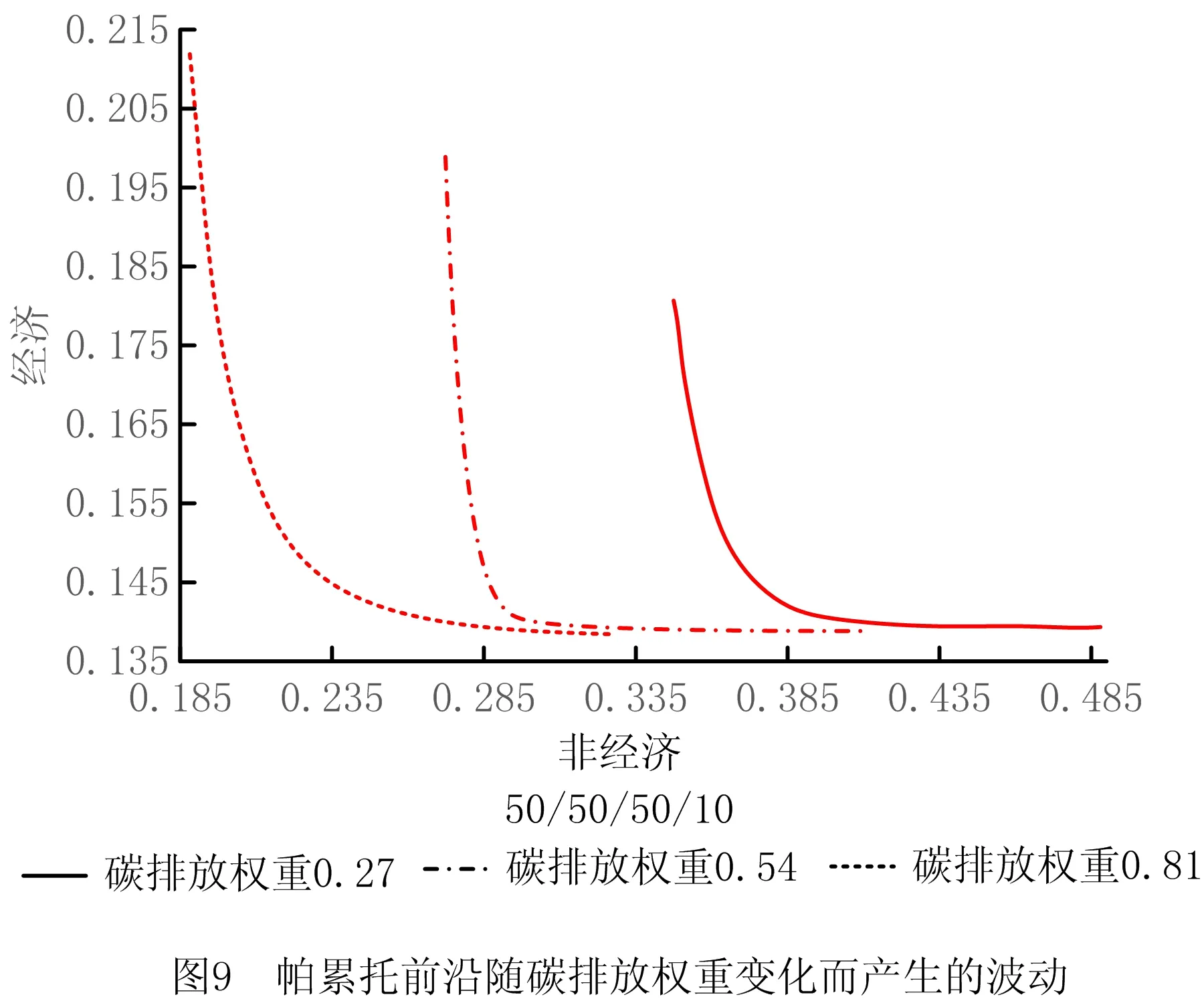
whilek 计算解森林每个多叉树个体的适应度 采用精英保留策略进行选择操作 得到其中最优多叉树个体best 自适应动态改变定点剪枝重组概率和随机节点置换概率 for i=1,2,…,populationSize do if random(0,1) 执行定点剪枝重组操作 if最大供货数小于上一层根节点产品或原材料需求量do 执行约束条件处理,调整多叉树个体 end if end if if random(0,1) 执行随机节点置换操作 if最大供货数小于上一层根节点产品或原材料需求量do 执行约束条件处理,调整多叉树个体 end if end if end for k=k+1 end while end 定义深度为h的多叉树T,表示为一个供应链网络设计方案。T有且仅有一个特定的根节点Root,其余节点可分为nl个互不相交的有限集TC1,TC2,…,TCnl。定义每个集合TCl={Cl,{Dlk},{Tlj},{Sli}}为T的子树,其中Cl表示当前子树TCl的根节点客户,{Dlk}表示该子树分销商层的节点集合,{Tlj}表示该子树制造商层的节点集合且存在重复节点,{Sli}表示该子树供应商层的节点集合且存在重复节点;TCl根为Cl,其余节点分别为{Dlk}元素个数len_Dlk个互不相交的子集(子树)TCDlk={Dk,{Tkj},{Ski}},其中{Tkj}表示该子树制造商层的节点集合,{Ski}表示该子树供应商层的节点集合且存在重复节点;TCDlk根为Dk,其余节点分别为{Tkj}元素个数len_Tkj个互不相交的子集(子树)TCDTlkj={Tj,{Sji}},其中{Sji}表示该子树供应商层的节点集合;TCDTlkj根为Tj,其余节点分别为{Sji}元素个数len_Sji个互不相交的子集(子树)TCDTSlkji={Si}。每个多叉树个体中相邻层节点rx、ry之间连接的权重Wxy表示两个节点rx、ry间的物流数量。 为了保证初始解森林的多样性,本文采用3种方法生成森林总数a%,b%和c%数量的个体树:1)单纯随机法;2)轮盘赌法;3)锦标赛法。 轮盘赌法以式(28)计算每层候选节点被选择的概率,根据概率选择节点。 (28) 式中:qa为该层备选供应链节点中第a个供应链节点被选择的概率;pa为此层该潜在供应节点的适应度;N为该层备选供应链节点的个数。每层供应节点的适应度计算如下: (29) (30) pkl= (31) 其中:pij为供应商层中备选供应商节点的适应度;pjk为制造商层中备选制造商节点的适应度;pkl为分销商层中备选分销商节点的适应度。根据每一层相应供应节点被选择的概率可以得到每个供应链节点x的累计概率cumx为: (32) 由式(28)~式(32)可知,备选的供应链节点适应度越小,被选择的可能性就越大。 与轮盘赌法不同,锦标赛法每次选择多个供应节点,根据每个供应节点的适应度值,选择其中适应度值最低的供应节点。 (33) (34) (35) (36) (37) (38) 重组后,若被选中节点rx对原父节点ry的供货数量Wxy (39) 式中newT为调整子树,与被选中节点rx具有相同父节点ry′,且newT向ry′提供的供货数量Wnew满足Wxy+Wnew=Wy′。 当交换层为第二层时,在此层选择一个点Cl,构造调整子树newT={Cl,{Dlk},{Tlj},{Sli}},则 (40) (41) 当交换层为第三层时,在此层选择一个节点Dk,构造调整子树newT={Dk,{Tkj},{Ski}},则 (42) (43) 当交换层为第四层时,在此层选择一个节点Tj,构造调整子树newT={Tj,{Sji}},则 (44) (45) 调整后,采用单纯形法对得到的多叉树个体重新分配各级的供应关系。 关于时间复杂度,当交换层为第二层时,时间复杂度为O(1);当交换层为第三层时,时间复杂度与分销商个数nk有关,故为O(nk);当交换层为第四层时,时间复杂度与分销商个数nk和制造商个数nj有关,故为O(nk+nj)。因此,时间复杂度范围为[O(1),O(1+2nk+nj)]。 为防止算法陷入局部最优,本研究使用随机节点置换操作提升种群多样性。具体操作为在各候选层中通过生成随机数并与该层的随机节点置换概率进行比较的方式判断该层是否执行随机节点置换操作,并将选中层中一个节点rx置换为rx′,从父代FTn中直接生成子代CTj。当置换层为第三层时,在此层选择一个节点Dk作为置换点,将FTn中TCDlk={Dk,{Tkj},{Ski}}置换为TCDlk′={Dk′,{Tkj},{Ski}},生成CTj=∂FTnTCDlk∪TCDlk′;当置换层为第四层时,在此层选择一个节点Tj作为置换点,将FTn中TCDTlkj={Tj,{Sji}}置换为TCDTlkj′={Tj′,{Sji}},生成CTj=∂FTnTCDTlkj∪TCDTlkj′;当置换层为第五层时,在此层选择一个节点Si作为置换点,将FTn中TCDTSlkji={Si}置换为TCDTSlkji′={Si′},生成CTj=∂FTnTCDTSlkji∪TCDTSlkji′。 在随机节点置换之后,若被置换后的节点rx′对父节点ry的供货数量Wx′y 当置换层为第三层时,在此层选择一个节点Dk,构造调整子树newT={Dk,{Tkj},{Ski}},则 =∂FTnTCDlk∪TCDlk′∪newT。 (46) 当置换层为第四层时,在此层选择一个节点Tj,构造调整子树newT={Tj,{Sji}},则 =∂FTnTCDTlkj∪TCDTlkj′∪newT。 (47) 当置换层为第五层时,在此层选择一个节点Si,构造调整子树newT={Si},则 ∪TCDTSlkji′∪newT。 (48) 关于时间复杂度,当置换层为第三层时,时间复杂度与分销商个数nk有关,故为O(nk);当置换层为第四层时,时间复杂度与制造商个数nj有关,故为O(nj);当置换层为第五层时,时间复杂度与供应商个数ni有关,故为O(ni)。因此,时间复杂度的范围为[O(nk),O(nk+nj+ni)]。 为平衡算法的收敛性和森林多样性,定点剪枝重组概率和随机节点置换概率采用自适应调整机制。当森林中多数个体相似性较高时,说明森林多样性较差,算法易陷入局部最优,故应提高随机节点置换概率并降低定点剪枝重组概率;反之,如森林中个体的相似性较低,则算法的收敛速度较慢,则应提高定点剪枝重组概率并降低随机节点置换概率以提升算法收敛性。 RSeq={y|y∈{1,2,…,nl}∨y∈{1,2,…,nk}∨ y∈{1,2,…,nj}∨y∈{1,2,…,ni}∨y∈{0}}。 (49) (50) 则当前解森林平均差异度为: (51) 式中:N为两个多叉树个体中实数化序列最大长度;minlen为两个多叉树个体中实数化序列最小长度;PS为解森林规模;xji,xjk为当前代解森林中的第i,k个多叉树个体实数化序列的第j维元素。则解森林差异度为: (52) 式中Ddmin、Ddmax分别为Ddik的最小值、最大值。根据diversity的大小自适应调整定点剪枝重组率或随机节点置换率,如式(54)所示。 (53) 式中:v为新的定点剪枝重组率或随机节点置换率;v′为上一代的定点剪枝重组率或随机节点置换率;η为变化因子;pΔ、p∇为差异度的临界值。 算法仿真以Java语言实现,实验运行环境为Inter(R)Core(TM)i7-7700 CPU @ 3.60 GHz CPU,16 GB RAM。算法参数如表5所示。 表5 实验参数设置 4.2.1 求解质量分析 本节依照某小型金属零部件制造产业设置了5个算例,算例规模分别按供应商数量/制造商数量/分销商数量设置为20/20/20、40/40/40、60/60/60、80/80/80、100/100/100。算例数据参考公众环境研究中心和自然资源保护协会合作研发的绿色供应链平台中的企业信息设置,具体如表6所示。计算各能源碳排放量的GHG排放因子如表7所示。对所有实例分别采用自适应进化算法(Evolutionary Algorithm 1,EA1)、非自适应进化算法(Evolutionary Algorithm 2,EA2)、非自适应纯随机进化算法(Evolutionary Algorithm 3,EA3)各执行20次,实验过程中得到各级供应关系的单纯形法通过CPLEX优化器实现。实验结果如表8所示。各算例的最优解和采用EA1、EA2、EA3执行得到的实验结果的对比如图3所示。 表6 实例参数设置 表7 GHG排放因子 续表7 表8 实验结果 续表8 从表8可以看出,在算例规模逐渐增大时,将EA1的平均解作为自适应进化算法的求解质量,该求解质量与最优解最大差距在5%以内,平均差距为3.25%,在小规模算例(20/20/20)时平均差距为1.42%,在大规模算例(40/40/40及以上)时平均差距为3.71%。EA1的平均解与EA2和EA3的平均值相比较,求解质量均有所提升。同时,根据最大值与最小值可以看出采用EA1比采用EA2和采用EA3的求解过程收敛效果更好。在相同的算例规模下,采用EA1比采EA2和采用EA3的求解质量更接近最优解。 从图3中可以看出,在相同的算例规模下,采用EA1的求解质量更接近最优解。同时可以看出,EA1的求解质量比EA3的求解质量提升效果要优于EA1的求解质量比EA2的求解质量提升效果。 4.2.2 求解时间分析 为分析算法的求解时间,本节依照某小型金属零部件制造产业设置了2组算例,第一组算例的规模分别按供应商数量/制造商数量/分销商数量/客户数设置为100/100/100/20、100/100/100/40、100/100/100/60、100/100/100/80、100/100/100/100,第二组实验用例的规模分别按供应商数量/制造商数量/分销商数量/客户数设置为20/20/20/20、40/40/40/40、60/60/60/60、80/80/80/80、100/100/100/100。算例数据取值范围如表6所示。对所有算例分别采用EA1执行20次,实验结果如表9所示,每组算例的求解平均时间变化趋势如图4所示。 表9 实验结果 从表9和图4中可以看出,在供应商数量、制造商数量、分销商数量固定时,EA1的求解时间随着客户的数量的增加而增加;在供应商数量、制造商数量、分销商数量、客户数按相同数量级同时增加时,求解时间随着可持续供应链候选商的数量的增加而增加,且两种增加速率接近。 4.2.3 灵敏度分析 为分析算法关键参数的灵敏度,本节采用4.2.1节中算例规模为40/40/40的算例4进行实验分析。 (1)迭代次数灵敏度分析 在其他参数相同的情况下,对不同迭代次数下的多叉树自适应进化算法各执行20次,得到平均近似解随着迭代次数增加的变化趋势如图5所示。 从图5中可以看出,平均近似解在迭代次数逐渐增大的情况下逐渐下降,在迭代次数达到150时下降缓慢,在迭代次数达到200时基本趋于不变。 (2)解森林规模灵敏度分析 在其他参数相同的情况下,对不同解森林规模下的多叉树自适应进化算法各执行20次,得到平均近似解随着解森林规模增加的变化趋势如图6所示。 从图6中可以看出,平均近似解在解森林规模逐渐增大的情况下逐渐下降,在解森林规模达到30时下降缓慢,在解森林规模达到50时基本趋于不变。 4.2.4 多目标优化效果分析 为了检验在经济、环境和社会三方面进行多指标优化的效果,本节采用4.2.2节中第2组算例分别对单一底线模型(只考虑经济侧的成本)和本文三重底线模型进行实验,实验结果如表10所示。单底线和多底线时的实验结果对比如图7所示。 表10 实验结果 由表10可知,在只以成本进行单底线优化时,所选供应链方案的成本较低,但环境侧的碳排放量、废气排放量、废水排放量、固体废物排放量较高,同时社会侧的创造就业数偏低,企业事故数和超标整改数却偏高。而在考虑经济侧的同时考虑环境侧和社会侧进行多底线优化时,供应链方案成本比考虑单一优化目标时的成本略有升高,但升高范围在5%以内;同时此种模式下,环境侧的碳排放量、废气排放量、废水排放量、固体废物排放量整体上均有不同程度的减少。其中,碳排放量最低比单底线时减少13.72%,最高可达到22.69%;废气排放量最低比单底线时减少8.68%,最高可减少12.12%;废水排放量最低比单底线时减少11.31%,最高可减少15.90%;固体废物排放量最低比单底线时减少16.19%,最高可减少24.17%。同时,社会侧的创造就业数最低比单底线时增加43.56%,最高可增加67.20%;企业事故数和超标整改数变化较为明显,比单底线时基本上可以达到100%的减少率。同时从表10和图7中可以看出,在进行经济侧、环境侧和社会侧三重底线优化时,制造业可持续供应链在其社会侧的优化效果最为明显,在制造业可持续供应链中制造商提供的就业数以及制造过程中发生的企业事故数和超标整改数优化效率均达到40%以上,企业事故数和超标整改数的优化效率变化趋势基本趋于稳定。制造业可持续供应链在其环境侧的优化效果较为明显,其中固体废物排放量的减少量最多,其优化效率在20.19%附近上下波动,最大波动为4%;其次减少量较多的是碳排放量,其优化效率在17.69%附近上下波动,最大波动为5.02%;废水排放量的减少量仅次于碳排放量,优化效率在13.05%附近上下波动,最大波动为2.85%;废气排放量的减少量低于废水排放量,优化效率在10.54%附近上下波动,最大波动为1.86%。在环境侧各指标的优化效率变化趋势中废气排放量较为稳定,但废气排放量的减少量没有其他指标的减少量明显;碳排放量的优化效率变化趋势波动较大,但是其减少量较大。综上,在制造业可持续供应链网络中纳入经济侧、环境侧和社会侧进行多底线优化可以有效的减少制造业企业的环境污染和提高其社会责任。 4.2.5 帕累托前沿分析 针对本文所提出的三重底线可持续供应链模型,本节采用文献[8]的方法,分析了该问题的帕累托前沿。由于帕累托集在解决三个以上优化目标问题时在可视化方面并不清晰,因此本文将环境侧和社会侧合并为一个优化目标(下文简称综合侧),绘制了二维帕累托曲线。其具体计算方法概述如下:首先,仅以经济侧目标函数作为优化目标,得到最优解作为该目标函数的下界,并以此情况下的综合侧目标函数值作为综合侧目标函数的上界;同样的,再仅以综合侧目标函数作为优化目标,得到最优解作为该目标函数的下界,并以此情况下的经济侧目标函数值作为经济侧目标函数的上界。然后依次将一个目标函数上下界之间等分得到n个边界值,再依次以该目标函数不大于每个边界值作为约束优化另一个目标函数,得到另一个目标函数的n个对应边界值,将两个目标函数的对应边界值组合可以得到一个前沿点。最后依照获取的前沿点集合拟合出帕累托前沿。 如图8所示,当经济侧目标函数值增大时,综合侧目标函数值减小;当综合侧目标函数值增大时,经济侧目标函数值减小。更重要的是,在经济侧目标函数值有一个较小升高时,综合测目标函数值即可获得一个较大的下降。由此可以看出,制造业企业在进行供应链决策时应将可持续发展纳入决策过程中,对经济效益、环境污染和社会责任进行整体协调,促进三者平衡发展,仅以较小的经济代价即可获取较大的环境和社会回报。 4.2.6 碳排放参数对帕累托前沿的灵敏度分析 针对本文所提出的三重底线可持续供应链模型,本节分析了碳排放权重对该问题帕累托前沿的影响。在碳排放权重增大时,废气排放、废水排放和固体废物排放按比例缩小,保证四者权重和不变。帕累托前沿随碳排放权重变化而产生的波动如图9所示。从图9中可以观察到,碳排放在非经济侧占据较重要地位,当其权重增大时,优化结果中的碳排放量降低,帕累托曲线中综合侧目标函数最大值最小值均减小,但同时也导致了经济侧的目标函数最大值增大。 为更好的观察碳排放权重对经济侧目标函数值和碳排放量的影响,本节同时分析了经济侧目标函数值与碳排放量间关系随碳排放权重提升而产生的变化,其结果如图10所示。当经济侧目标函数值相同时,碳排放权重越大,碳排放越小,综合侧目标函数值越小;在综合侧取得最小值的情况下,碳排放权重越大,碳排放越小,经济侧目标函数值越大。由此可以看出,制造业企业进行供应链决策时,在相同的经济投入代价的情况下,更大的碳排放权重可获取更大的环境和社会回报;但若追求最低碳排放量,企业的经济代价会显著提高。 本研究针对可持续发展的三重底线,提出了制造业可持续供应链的主要优化指标及量化方法,为其构建了一个新的多层次、多产品类型、多能源模式的混合整数规划模型,并将可持续指标进行了整合,降低了求解难度。在模型求解方面,基于小型金属零部件制造产业的真实数据设置仿真算例并进行了大量实验。实验表明,本文提出的多指标数学模型和基于多叉森林的自适应进化算法可以高效解决制造业可持续供应链网络设计问题,为制造业企业的可持续发展提供决策辅助。在求解质量上,与最优解相比较,最小平均差距为1.42%,最大平均差距为3.71%,平均差距在5%以内,各实例平均差距的均值为3.25%。在求解时间上,最小时间为12.4s,最大时间为48.9s,小规模算例的平均时间为12.6s,较大规模算例的平均时间为31.1s。 本文研究发现,在经济、环境和社会三方面将多指标优化与单底线模型(只考虑经济侧的成本)相比较,多目标优化比单底线模型成本有所提高,但是提高率没有超过单底线模型成本的5%,平均提高率为4.86%。碳排放量、废气排放量、废水排放量、固体废物排放量、企业事故数和超标整改数则在整体上均有较大程度的减少,其中碳排放量平均减少17.67%;废气排放量平均减少10.54%;废水排放量平均减少13.05%;固体废物排放量平均减少20.19%;创造就业数平均增加56.70%。因此,制造业企业在进行供应链决策时应将可持续发展纳入决策过程中,对经济效益、环境污染和社会责任进行整体协调,促进三者平衡发展,使制造业企业更加积极的参与处理环境污染问题和承担社会责任。相对于其他企业,污染程度较低、事故和整改次数较少的候选企业更容易被选中为合作伙伴,这种模式可以激励企业更加主动的承担环境责任和社会责任,使企业从制造源头降低碳排放量、废气排放量、废水排放量和固体废物排放量,减少自身污染种类和排放总量。同时,以上决策模式也会促进污染程度较严重、事故和整改次数较高的企业提高社会责任感,加强自身监管,通过改造升级降低污染排放,减少事故、违规和整改等情况的发生。 综上所述,制造业企业在进行供应链决策时,应当在考虑经济效益的同时,将环境侧和社会侧的各项指标纳入考虑范围,同时制造业企业需要树立可持续发展的供应链决策意识,加强自身可持续供应链管理模式,增加制造业可持续供应链中各供应商、制造商、分销商和客户之间的可持续发展战略协作,使制造业供应链整体的可持续发展进入良性循环。3.1 多叉树结构设计
3.2 初始解森林生成
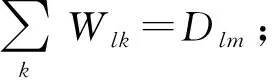

3.3 定点剪枝重组操作
3.4 随机节点置换操作
3.5 自适应机制

4 实验与分析
4.1 实验环境及参数

4.2 实验结果与分析










5 结束语
