对一道教材习题的研究性学习

广东省广州市铁一中学(511447) 刘 国

1 问题呈现

设x,y为正数, 且x+y= 1, 用反证法证明

详见《普通高中课程标准试验教科书.4-5(选修)》(人教A 版)第29 页习题2-3 第4 题.此题是一道典型条件不等式证明题,课本要求用反证法证明.如果将此题改为：

设x,y为正数,且x+y=1,证明

再要求同学们证明此题,同学们会用反证法吗? 同学们会用什么方法证明呢? 解题的价值并不在于答案本身,而在于弄清“是怎样想到这种解法或证法的”,“是什么促使你这样想,这样做的”,“怎样做更有效”? 事实上,一次解题或证题,就像是一次旅行.在这个旅行中,如果我们能用“心灵”去感知、感受,如果我们能放飞解题的“心灵”,那么,无论是什么数学问题,也无论你的思路是否顺畅,一路走来,处处背景是风景.此题如果只用反证法来证明,那么这次解题之旅时失败的,照本宣科使用教材的教学时低效的.

2 证法探究

2.1 用反证法证明

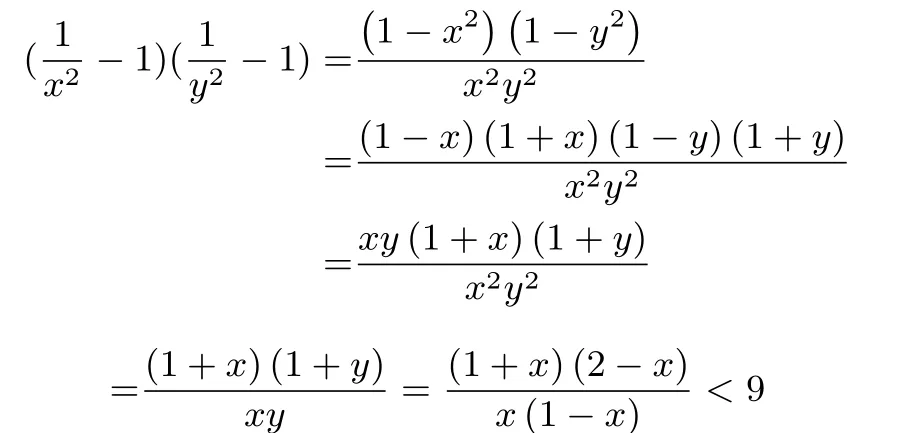
得(2x-1)2＜0,这是不可能的.所以9.

以上证法是教师教学用书给出的证法.

2.2 用比较法证明

证法2：由x+y=1,所以

用比较法证明不等式是最简单、最基本、最常见的方法,是证明不等式的首先方法.

2.3 用综合法证明

证法3：由x+y= 1 得1- x=y, 1- y=x, 因为同理所以

又 1 =x+y≥所 以≥ 4, 所 以当且仅当x=y=时取等号,则

证法4：由x+y= 1 得-1 =同理

所以

当且仅当x=y=时取等号,则

证法5：由证法3 变形得

当且仅当x=y=时取等号,则

证法6：因为x2和y2都是正数,所以要证成立,只需证明(1-x2)(1-y2)≥9x2y2成立,展开得1-x2-y2+x2y2≥9x2y2,只需证明8x2y2+x2+y2-1 ≤0,又x ＞0,y ＞0,x+y=1,故只需证明8x2y2+x2+y2-(x+y)2≤0,即8x2y2-2xy≤0,因为x ＞0,y ＞0,x+y=1,故1=x+y≥故xy≤由xy≤成立,得成立.

2.5 用三角代换证明

证法7：设x=cos2θ,y=sin2θ,θ /=k ∈Z,则

当且仅当x=y=时取等号,则

2.6 用等差数列证明

证法8：由已知条件, 可设x=其中因为≥1+8 = 9, 当且仅当d= 0 时取等号, 当且仅当x=y=时取等号, 则由x+y=1,可以联想到是x与y的等差中项.

2.7 用向量法证明

证法9：由证法4 的变形, 可以构造向量a=由|a|2|b|2≥ (a·b)2, 得= 9, 所以≥9,其实柯西不等式和向量法实质是一样的.

2.8 用换元法证明

2.9 用导数法证明

证法11：由x+y= 1 得y= 1- x,0＜x ＜1, 令M=则M=

令M= 0 得x=当0＜ x ＜时,M′ ＜0, 当＜x ＜1 时,M′ ＞0, 故当x=时,Mmin= 9, 所以

3 变式探究

在数学课堂教学中,教师应该注意给学生营造不同的问题情境,通过变式研究,可让学生通过自己一系列思维的加工发展自己的创造思维和创新能力.

变式1：已知x,y为正数, 且x+y= 1, 求证

变式2：已知x,y为正数, 且x+y= 1, 求证

变式3：已知x,y为正数, 且x+y= 1, 求证2＜

上述3 个变式易证,留给读者完成.

变式4：已 知x,y为正数, 且x+y= 1, 求证

证明：因为x,y为正数,且x+y=1,所以1=x+y≥≥16,所以

当且仅当x=y=取等号,则

变式5：已知x,y为正数, 且x+y= 1, 求证≥(2n-1)2(n ∈N∗).

证明：因为x,y为正数,且x+y=1,所以

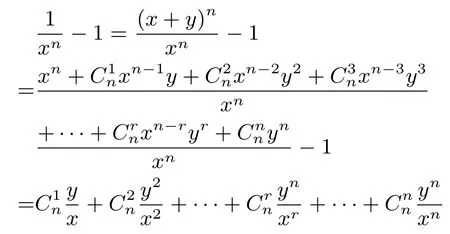
当且仅当x=y=取等号, 则(2n-1)2(n ∈N∗).

变式6：已知x,y为正数, 且x+y= 1, 求证

证明：由题意可设x= cos2θ,y= sin2θ,θ /=则

令t= sin2θcos2θ, 则0＜ t≤-2,f′(t) = 2t -而0＜t≤所以f′(t) = 2t -＜0, 故f(t)在0＜t≤上单调递减,所以当t=时,f(t)由最小值当且仅当x=y=取等号,则

变式7：已知x,y为正数, 且x+y= 1, 求证

证明：因为x,y为正数, 且x+y= 1,x2+y2=(x+y)2-2xy=1-2xy,x3+y3=(x+y)3-3xy(x+y)=1-3xy,x5+y5=(x3+y3)(x2+y2)-x2y2(x+y) =5x2y2-5xy+1,所以

因为x,y ＞0,由基本不等式可得1 =x+y≥所以

设t=xy,f(t) =t3+-5,0＜ t≤因为f′(t) = 3t2-而当0＜ t≤时,f′(t) =＜0, 所以f(t) 在0＜t≤上单调递减,所以f(t) ≥当且仅当x=y=取等号,则

变式8：已知x,y,z为正数, 且x+y+z= 1, 求证

变式8 易证,留给读者完成.

4 教学感悟

4.1 精心设计问题,促进深度学习

美国心理学家布鲁纳指出：“教学过程是一种提出问题和解决问题的持续不断的活动,思维永远是从问题开始.”因此,精心设置系列问题,为学生的学习活动搭建切当的平台,对于促进学生的自主学习和深度学习时非常关键的,笔者及时扑捉教学信息,设计问题序列,分组联动,诱导学生进行探究, 用问题驱动学生的思维并使学生参与到课堂活动之中,难度由低到高,形式由简洁直观到隐晦现象.通过问题串,让学生们自然地构建新知识,应用新知识,反思新知识,从不同的角度理解新知识,最后提升到综合运用所学知识解决问题的思维水平,追求一种自然,流畅的教学节奏,取得了良好的教学效果.

4.2 稚化教师思维,引领学生探究

现代认知心理学认为,新学习的知识必须纳入原有的认识体系,并在原有的认知结构中找到联系点,结合点,才能将新知识同化,牢固地掌握新知识,新课程提倡关系学生的认识特点,注意站在学生的角度,精心创设问题情境,诱发学生思维的积极性,用卓有成效的启发引导,促使学生的思维活动持续发展,备课首先应该备学生,教师应非常熟悉学生的知识基础和认知水平及学习的薄弱之处,要善于改变自己身份,稚化自己的思维,从学生的角度审视问题.对于课堂中问题设计,坚持低起点,高落点,引导学生观察、归纳、体验,进行自主探究,激发学生的学习兴趣,锻炼学生的思维能力,为学生的全面发展和终身学习打下良好的基础.

4.3 及时调整预设,实现精彩生成

在新课程改革的教育理念下,数学课堂教学即要体现其应用价值,又要体现数学本质.数学课堂应逐步走向“学习参与、交往互动、共同发展.”课堂教学问题过程更是一个个活泼的头脑在教师预设好的问题情境中的交流、对话与活动的过程,是“精心预设”与“动态生成”和谐统一的过程.我们应该创造有利条件让学生在自主的学习交流和互动中逐步完善认识,丰富生成的空间,使课堂在师生的共同创造中变得充满灵性、充满智慧、充满活力.

4.4 反思教学,促进教师专业成长

加强习题研究,促进教师专业成长.现在习题大多都有答案,有些教师认为看看答案怎么解就可以了,这种观点时错误的.一道由价值的习题,一般都有着丰富的内涵.教师应高屋建瓴,全面展开试题研究,在解题的基础上进一步研究它的立意、来源、解法、变式、推广、应用等,充分挖掘习题的价值,并运用到教学中,从而不断提高教研水平,促使教师专业成长.

当前许多教师不重视课本例习题,认为课本例题、习题简单、不能应对高考.重视课本不能只停留在表面,要通过一题多变、一题多解、多题一解等,把知识目标、能看目标落实到实处,真正达到高效教学.

课本例题、习题都经过专家们的千挑万选,蕴含着数学思想和方法.《普通高中数学课程标准(试验) 》、《考试说明》提出重视课本的基础和导向作用,所以在命题时多选择一些课本上的原题或者是课本例题、习题的变式,使学生更加重视课本内容的学习.