PMSM电流预测控制参数误差量化分析方法*
2021-08-12牟筱宁曾凡铨崔业兵宋树伟
牟筱宁,曾凡铨,周 阳,崔业兵,宋树伟
(1.上海航天控制技术研究所·上海·201109;2.上海伺服系统工程技术研究中心·上海·201109)
0 引 言
由于采用了永磁体励磁,永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)具有结构简单、体积小、功率密度高和转矩脉动小等优势[1]。在对控制精度和可靠性有严格要求的应用场合(如航空航天、高精度数控加工机床、工业机器人等领域)中,均已经得到了广泛应用[2-3]。
永磁同步电机伺服系统一般采用三环级联的层次式反馈控制结构。电流环作为电机的内环,其动态性能及稳态控制性能直接决定着电机的控制性能[4]。微处理器的性能取得了不断发展,使得在一个控制周期内便可以完成更加复杂的控制算法,而电流预测控制技术已成为了近年来的研究热点[5]。电流预测控制技术使用电机和逆变器的离散时间模型预测下一周期的电流响应,从而提前产生响应动作,缩短控制延时,提高电流环的带宽与动态响应能力[6-9]。
按照电压矢量作用方式的不同,永磁同步电机电流预测控制技术主要可分为直接电流预测控制、双矢量电流预测控制和PWM电流预测控制三种[10]。其中,PWM预测控制根据电机及逆变器的离散时间模型精确计算当前时刻所需的电压,并将该电压的数值通过PWM调制转换为逆变器的开关顺序的控制方法。该方法具有纹波较小的交直轴电流响应,相电流谐波含量较低,且谐波集中分布在开关频率及其倍数频率附近[11]。但是,PWM电流预测控制是基于模型的控制方法,电机定子电阻、电感与磁链的参数变化,均会导致电流控制出现振荡或静差[12]。
为消除参数误差对电流预测控制的影响,研究人员进行了广泛而深入的研究[10,13-14]。文献[10]分析了电感和磁链参数误差对电流静差的影响。通过在d轴电流控制中加入积分,同时动态调整控制器电机模型的磁链参数,消除了电流静差;文献[13]详细讨论了电感对系统稳定性的影响;文献[14]对电机的电感和磁链进行了在线参数辨识,但该方法需要占用大量的系统资源。本文在文献[10]的基础上,从PWM电流预测控制的模型出发,重新推导出了电阻、电感和磁链参数误差与电流静差的函数关系,引入了参数偏差因子,量化分析了电机参数误差与产生的电流静差之间的关联规律。
本文首先介绍PWM电流预测控制技术的基本原理,对电流静差的产生进行数学推导,分析参数变化与电流静差产生的内在关系。在此基础上,引入偏差因子反映电机参数的变化大小,总结出误差变化与静差变化之间的规律。最后,通过Matlab/Simulink仿真平台进行验证,验证了二者之间的制约关系。
1 PWM电流预测控制
本文以表贴式永磁同步电机模型为基础,采用id为0的矢量控制方式。通常选择同步旋转坐标系d-q下的数学模型,其定子电压方程可表示为
(1)
式中,ud、uq分别是定子电压的d-q轴分量;id、iq分别是定子电流的d-q轴分量;R是定子电阻;ψd、ψq为定子磁链的d-q轴分量;ωe是电角速度。
定子磁链方程为
(2)
式中,Ld、Lq分别是d-q轴电感分量;ψf为永磁体磁链。
将式(2)代入式(1),可得定子电压方程为
(3)
根据定子电压方程式(3),选择电机电流为状态变量。对于表贴式永磁同步电机,有Ld=Lq=L,并可得到状态方程如下
(4)
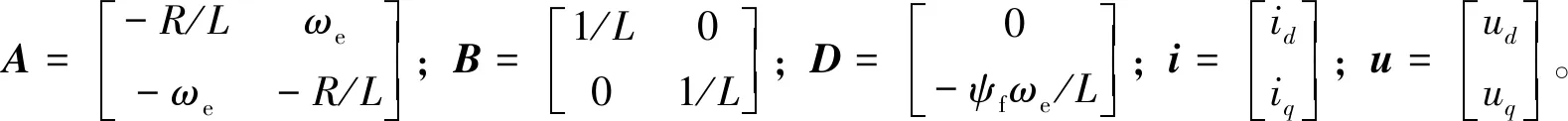
状态方程式(4)的通解可表示为
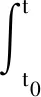
(5)
为了得到系统离散化的电流状态方程,在采样时间T较小的前提下,可认为系统输入电压u和反电势D在kT~(k+1)T时间间隔内恒定。令t0=kT、t=(k+1)T,电流状态方程(5)的离散通解为
i(k+1)=Aφi(k)+A-1(Aφ-I)Bu(k)+
A-1(Aφ-I)D(k)
(6)
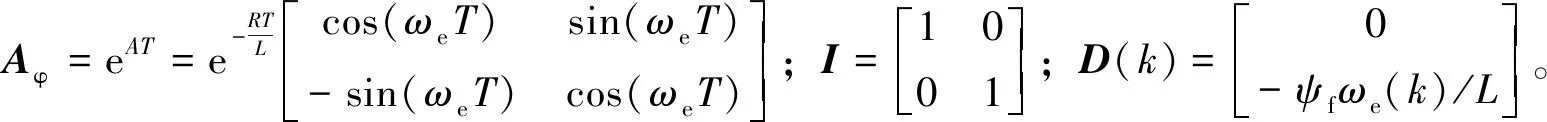
当采样时间T足够小时,可做如下近似
(7)
由此,可以得到简化后的电流预测模型为
i(k+1)=F(k)i(k)+G(k)u(k)+H(k)
(8)

u(k)=G-1(k)[i*(k+1)-F(k)i(k)-H(k)]
(9)
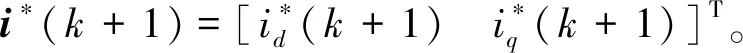
将下一时刻电流指令i*(k+1)和当前电流反馈值i(k)代入式(9),便可计算出使电机电流精确跟随指令所需的电压矢量u(k)。将生成的电压矢量通过SVPWM进行调制,以生成所需的开关信号并将其作用于开关器件。PWM预测控制的结构如图1所示。其中,ia、ib、ic为电机三相电流的采样值。
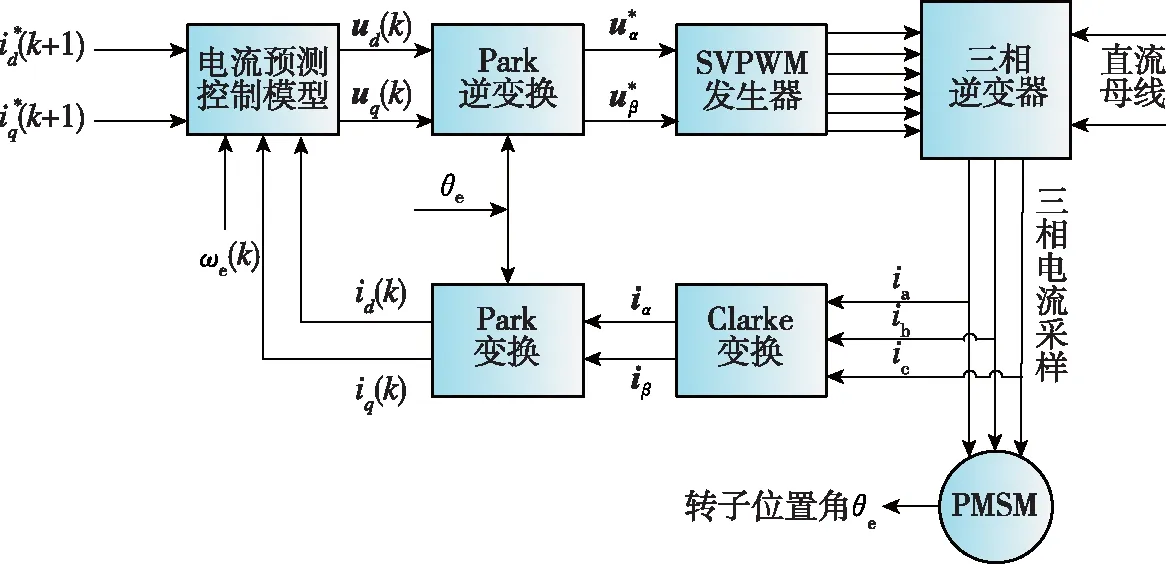
图1 PWM电流预测控制结构图Fig.1 Block diagram of PWM predictive current control
2 电流静差成因分析
电机在运行过程中,电机定子电阻、电感和磁链会受温度、工况等因素影响而发生参数值变化,使得电机的实际参数值与控制器模型初始值之间存在误差。PWM预测控制是基于模型的预测控制方法,电机参数的变化对预测控制性能有很大影响,这使得电流预测值与电流给定值之间产生了静差。下文将首先分析产生电流静差的原因。
电流预测控制的控制过程为:在第一个控制周期中,根据电流指令i*(k+1)和上一时刻的电流反馈i(k),依据控制器中电机的原始参数,计算下一个控制周期所需的电压矢量u(k);在第二个控制周期中,将由上一时刻计算得到的电压矢量u(k)作用于当前电机,产生新的i(k+1)。将式(9)代入式(8),可得电流表达式
i(k+1)=F0(k)i(k)+G0(k)u(k)+H0(k)
(10)
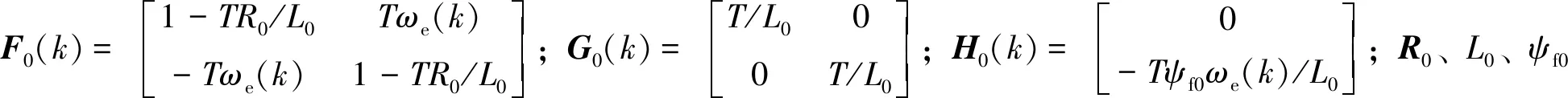
考虑电阻参数误差,根据高精度永磁同步电机参数,电阻值通常为数十mΩ。当电机工作在实际生产工况时,电阻会有不超过±10%的参数变化。电流环的采样频率一般设置为10kHz,电感通常设置为数百mH。按照电阻最大波动计算系数矩阵F(k)中的TR/L项,TR/L项会有不超过1‰的变化。因此,电机电阻参数误差对预测控制的影响较小。同时,由于TR/L<<1,可认为1-TR/L≈1。因此,F(k)和F0(k)可简化为FI(k)
(11)
将式(11)代入式(10),可以得到d、q轴电流响应与给定电流的关系
(12)
式中,ΔL和Δψf分别为实际电机参数与控制器电机模型参数的差值,即有ΔL=L0-L,Δψf=ψf-ψf0。
对预测系统的稳定性进行分析。在电机控制系统中,电机的机械时间常数远大于电气时间常数,转速变化相对于电流变化是十分缓慢的。因此,可将式(12)中含有ωe(k)的项视为扰动项。对式(12)进行Z变换,可得到系统的闭环传递函数
(13)
由上式可知,系统的特征根为z=1-L/L0。根据离散控制系统稳定的充要条件,可得到系统的稳定条件为
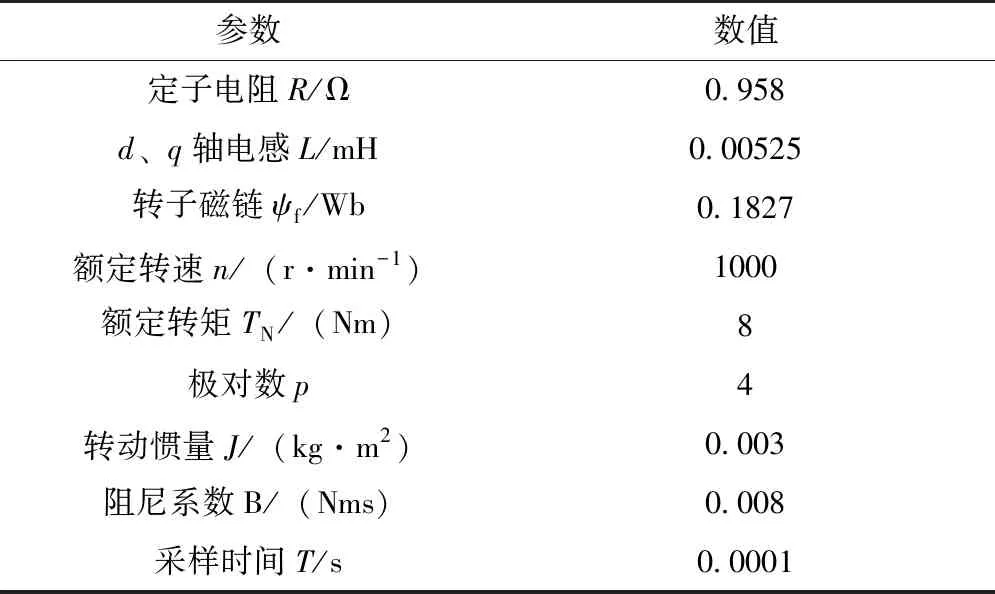
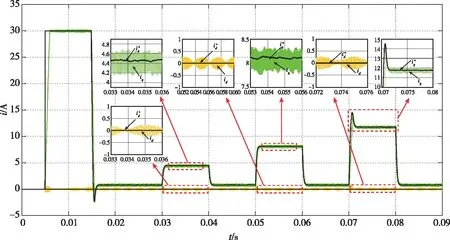
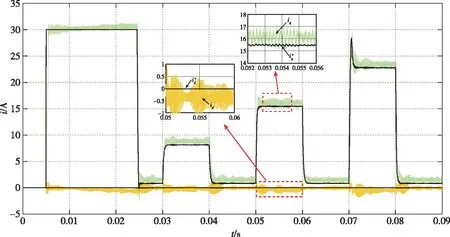
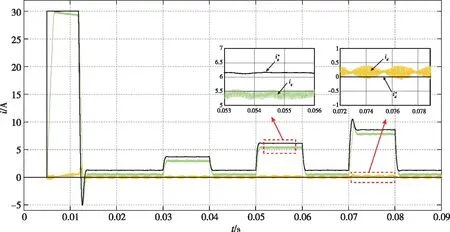
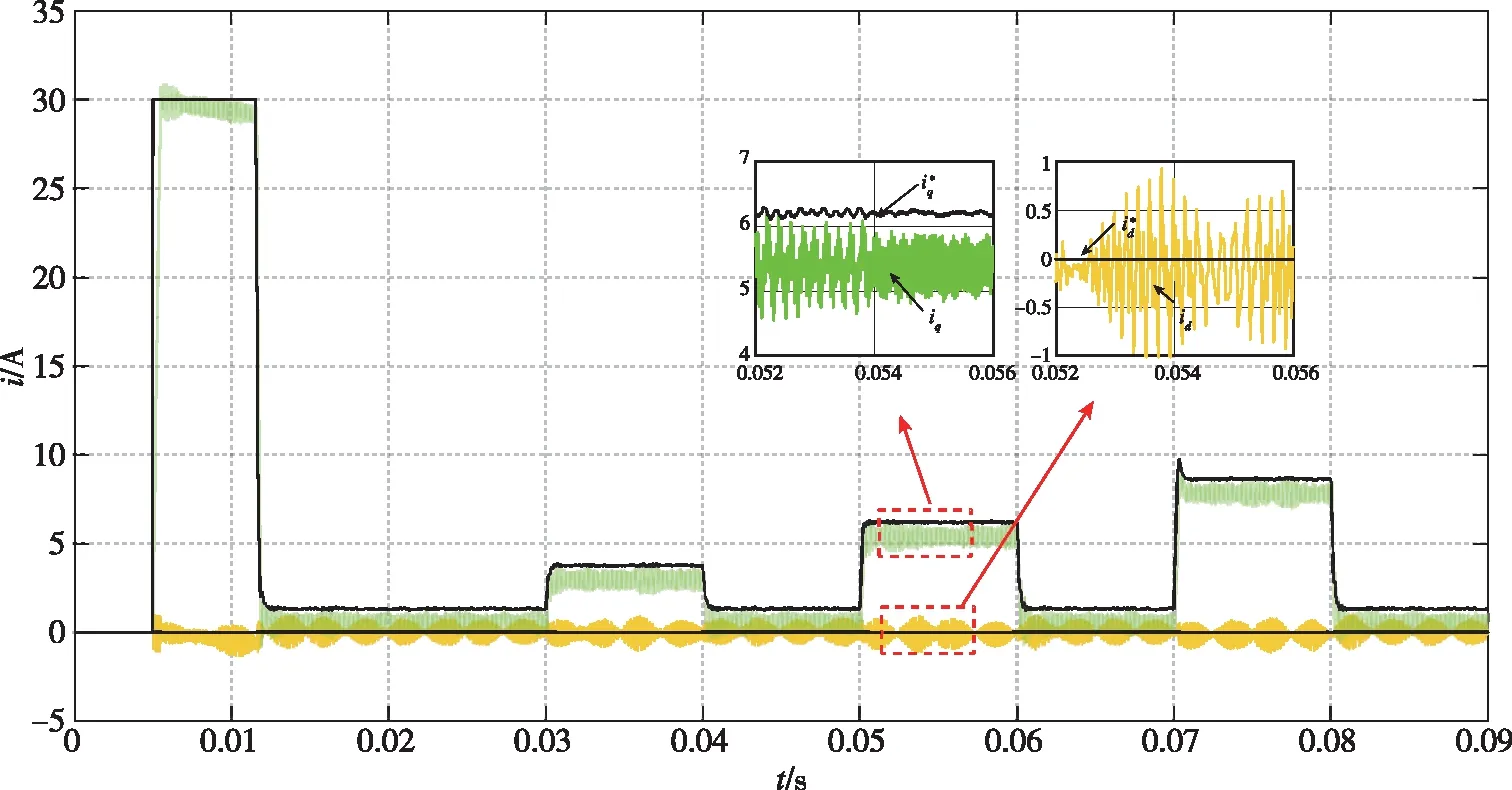
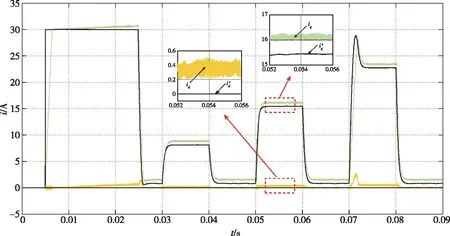
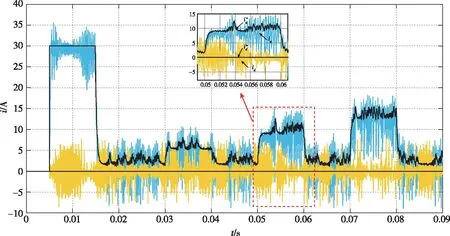
0 (14) 即控制器电感小于电机实际电感的2倍。 在稳态状态时,可以认为id(k)=id(k+1),iq(k)=iq(k+1)。由此,可推导出d、q轴电流静差公式为 (15) 由式(15)可知,电感参数偏差影响d轴电流静差,电感和磁链参数偏差影响q轴电流静差。此外,d、q轴电流静差与采样时间T、转速ωe和iq(k)均有直接关系。 为了更加直观地描述参数误差对电流静差的影响,可引入电感偏差因子α和磁链偏差因子β来定量分析影响的大小,定义 (16) 将式(16)代入式(15),可以得到d、q轴电流静差与偏差因子间的关系 (17) 由上文的系统稳定性分析可知,当α>-0.5时,系统稳定可控,静差的大小与α正相关;当α≤-0.5时,系统不稳定,电流会出现振荡发散。 由式(17)可得到d轴电流静差与电感偏差因子α之间的制约关系,如表1所示。 表1 d轴电流静差与电感偏差因子α的关系表Tab.1 Table of the relationship between d-axis static current error and inductance deviation factor α 由表1中的关系可知,当电机正转、电磁转矩为正时,d轴电流静差的产生与磁链参数误差无关,只与电感参数误差有关。同时,电感值偏差越大,产生的d轴电流静差越为明显。在id为0的控制中,当电机的实际电感值大于控制器电机模型的电感参数时,d轴电流响应大于0;当电机的实际电感值小于控制器电机模型的电感参数时,d轴电流响应小于0。 分析q轴电流静差,得到如表2所示的关系。 表2 q轴电流静差与α、β的关系表Tab.2 Table of the relationship between q-axis static current error and α、β 由表2的数据可知,电机正转、电磁转矩为正且不考虑磁链参数误差,当电机实际电感值与控制器电机模型电感参数存在偏差时,q轴电流响应小于q轴电流给定值。当电感参数准确时,仅存在由磁链参数误差引起的q轴电流静差。当实际磁链参数大于电机模型磁链参数时,q轴电流响应小于给定值;当实际磁链参数小于电机模型磁链参数时,q轴电流响应将大于给定值。 电机仿真参数如表3所示,电流环控制频率设置为10kHz,仿真在Matlab/Simulink中进行。 表3 电机仿真模型参数Tab.3 Simulation parameters of the motor 仿真条件设置为:直流母线电压311V,在0.005s转速阶跃给定从0到1000r/min;在0.03s突加0.5倍额定负载,在0.04s突卸负载;在0.05s突加额定负载,在0.06s突卸负载;在0.07s突加1.5倍额定负载,在0.08s突卸负载。 本节采用所提出的电流预测控制方法,对上述电机进行了仿真测试。图2是d、q轴电流在模型参数准确时的响应曲线;图3~图7是d、q轴电流在电感和磁链参数失配时的响应曲线。其中,黑线为给定的电流指令。 图2 无参数误差时的电流响应仿真波形Fig.2 Simulation results of current response without parameter mismatch 图3 α=-0.5、β=-0.5时的电流响应仿真波形Fig.3 Simulation results of current response (α=-0.5,β=-0.5) 图4 α=0.5、β=0.5时的电流响应仿真波形Fig.4 Simulation results of current response (α=0.5,β=0.5) 图5 α=-0.5、β=0.5时的电流响应仿真波形Fig.5 Simulation results of current response (α=-0.5,β=0.5) 图6 α=0.5、β=-0.5时的电流响应仿真波形Fig.6 Simulation results of current response (α=0.5,β=-0.5) 图7 α=-0.7、β=0时的电流响应仿真波形Fig.7 Simulation results of current response (α=-0.7,β=0) 由图3~图6可以看出,电机在参数不准时会产生d、q轴电流静差,且电流静差与第3节得出的分析规律一致。当实际电感与磁链参数相较于控制器原始数据偏大时,引起的静差现象更为明显。由图7可以看出,当电机实际电感小于额定电感的一半时,电流会出现振荡发散,由此验证了上文所提出的稳定域。 本文依据PWM电流预测控制的基本原理,从理论上分析了d、q轴电流静差产生的原因,对电机参数误差与电流静差间的制约关系进行了分析。引入偏差因子α和β描述了当电机电感和磁链参数变化时,d、q轴电流静差的变化情况。通过判定α和β的大小,简单、形象地反映了电流响应与给定电流间的量化关系,并通过仿真验证了所提方法的实用性和准确性。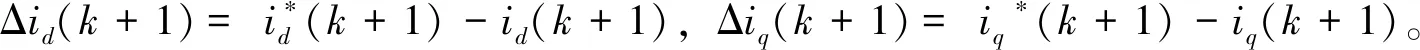
3 参数误差量化分析


4 仿真结果及分析
4.1 仿真条件
4.2 参数误差条件下的电流静差情况
5 结 论
