不同流速比超声速混合层气动光学效应研究*

邢博阳，蔡 彬，杨 波，张 斌

(1.上海交通大学 航空航天学院·上海·200240；2.上海航天控制技术研究所·上海·201109)

0 引 言

红外制导是导弹精确打击的主要制导手段之一。在制导过程中，光束穿过光学导引头后的光场质量是保证精确制导的重要参数。飞行器在以高超声速飞行时，其光学窗口上方的冷却喷流和远场自由来流之间会形成含有激波、膨胀波、混合层等的复杂流场结构。光束在穿过超声速混合层的非均匀介质后，会出现严重的导致模糊、偏移、抖动的气动光学效应[1]。制冷剂喷流与外部来流形成的混合层流场结构，是产生气动光学效应的一个重要来源[2]。研究光束的波前畸变与混合层流动结构之间的内在关系，是研究气动光学效应的重要途径。深入认知气动光学效应的产生机理，有助于采取有效的控制方法来降低气动光学效应对飞行器光学系统成像质量的影响。

本质上而言，气动光学效应的产生源于光束所穿越流场区域的内部流体密度分布的不均及密度分布的时变特性。在大量实验和工程实践中，剪切层(主要包括混合层和边界层)的气动光学效应能够体现一般气动光学问题的本质特征[3]，工程中的实际气动光学问题往往是多个剪切层气动光学效应的叠加。其中，由混合层导致的气动光学效应所占比重更大[4]。基于这一认识，本文将混合层作为典型流场，并以此开展针对气动光学效应产生的内在机理和气动光学效应校正等方面的研究。

现有的研究结果表明，混合层流场由不同尺寸的涡结构所控制，涡结构主导了混合层流场的密度脉动和速度脉动特性[5]，因而涡结构是混合层气动光学效应产生的根本因素。Childs[6]采用LES方法对可压混合层进行了数值模拟，并采用光线追踪方法研究了可压混合层带来的气动光学扰动。Kennedy等[7]对可应用于可压缩混合层的数值模拟方法进行了研究。在超音速混合层流动稳定性方面，Sandham[8]采用数值方法研究了可压缩混合层的线性稳定性。近些年，学术界出现了很多基于流场中涡结构的演化的受控混合层的研究。张冬冬等[9]通过直接数值模拟求解了Navier-Stokes方程，研究了涡结构的特性与入流激励参数之间的定量关系。郭广明等[10]采用大涡模拟方法对脉冲激励下超声速混合层流场中涡结构的演化机理进行了研究，总结出了涡结构的平均对流速度与脉冲周期的乘积近似等于涡结构的空间尺寸。在混合层试验研究方面，易仕和等[11-12]使用平面激光散射技术清晰地展示了超声速混合层流场中的涡结构，并对涡结构的流动特点及时间演化规律进行了研究。综上所述，目前对于混合层的研究离不开对流场中多尺度的涡结构演化特性的研究。因此，光束在穿越混合层时所产生的气动光学效应也就与流场中涡结构的动力学特性密切相关。

在工程领域中，导弹导引头侧窗的外部来流流速相对恒定，因此如何控制喷流速度、减小气动光学效应是研究的重点。本文聚焦了不同流速比的超声速混合层气动光学效应，对混合层流场涡结构的演化进行了研究，将混合层气动光学效应与流场涡结构特性进行了关联，采用大涡模拟方法对不同流速比的混合层进行了数值模拟，并通过仿真得到了不同条件下的气动光学效应。与此同时，本文还研究了光束波长和光束布置位置等相关光学参数对混合层气动光学效应的影响。

1 数值方法

1.1 LES数值方法验证

本文采用大涡模拟 (Large Eddy Simulation,LES)算法研究了超声速混合层流动。LES是介于直接数值模拟(Direct Numerical Simulation,DNS)与雷诺时均Navier-Stokes方程之间的一种数值方法，其现已发展得比较成熟。本文不对LES方法本身进行介绍，而是利用Goebel-Duttonh[13]实验条件对LES方法进行验证。混合层计算区域的长度为500mm，宽度为300mm，上下两股平行来流之间的尖劈厚度为0.5mm。为了方便计算，取混合区的长度为300mm，高度为48mm，定义流场特征长度H为48mm。将流场网格划分为两块，总网格数为901×152×2，将流场网格从混合层上下边界向混合层中间加密。上下来流组分都是空气，与实验一致，流场参数如表1所示。其中，Ma表示来流马赫数，U表示来流速度，T表示来流温度，P表示来流压强。

表1 Goebel-Dutton混合层实验流动参数Tab.1 Inlet flow parameters of the Goebel-Dutton Experiment

设U1为上方来流速度，U2为下方来流速度，ΔU=U1-U2。定义混合层厚度为速度值为某一流向速度剖面U1-0.1ΔU到U2+0.1ΔU两点之间的垂直距离，计算x=150mm的剖面混合层的时均流向速度，并将其与Goebel-Dutton的实验值进行对比，得到的结果如图1(a)所示。由图1(a)可以看出，二维流场数值模拟结果与试验值吻合良好。将x=150mm和x=200mm处的湍流强度时均统计结果与试验结果进行对比，得到的结果如图1(b)所示。由图1(b)可以看到，不同流向位置处的时均流向速度剖面和流向脉动速度剖面与Goebel-Dutton的实验数据都具有较好的一致性，这验证了所使用的LES方法在模拟超声速混合层流场方面的可靠性。

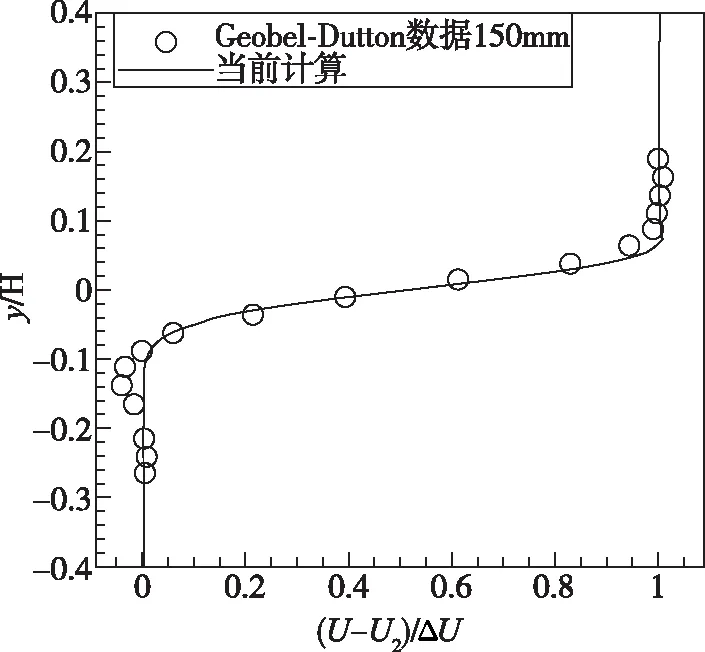
(a)时均流向速度剖面图

1.2 光线追踪方法

为研究光束穿过混合层流场的气动光学效应，本文采用了基于流场网格和直接模拟的光线追踪技术，这种方法基于光沿着直线传播的假设，可以通过光线追踪模拟光线在非均匀介质中的运动轨迹，进而得到一系列的气动光学评价参数。光线根据折射定律，在网格交界面处发生折射、反射或全反射。通过对光线通过流场的路径进行积分，可以得到每根光线的光程(Optical Path Length,OPL)，计算公式如下。其中，c为光线积分路径

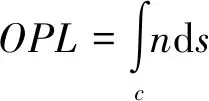
(1)

式中，n是光线通过每一个网格的折射率，可由下式得到

n=1+KGDρ

(2)

式中，ρ为所在网格的介质密度，KGD常简称为G-D系数。

在红外区域，标准的G-D系数随波长变化的关系式近似如下表示

KGD=(1+7.52×10-3/λ2)×2.23×10-4

(3)

式中，λ为波长，单位为μm。

进而，可以得到所有光束的光程差(Optical Path Difference,OPD)，尖括号表示空间平均

(4)

2 不同流速比二维混合层流动特征

2.1 算例设置

本文采用的是N.Chinzei[14]的试验数据，试验条件如表2所示。混合层流场上方高速来流马赫数M1为2.3，低速侧的来流马赫数M2分别为0.65、0.80、1.40。u1和u2分别表示上、下游来流的速度，速度比r=u2/u1，分别为0.39、0.47、0.74。试验段流场的长度为300mm，高度为47mm。在给定的试验段长度范围内，这些混合层能够充分发展。

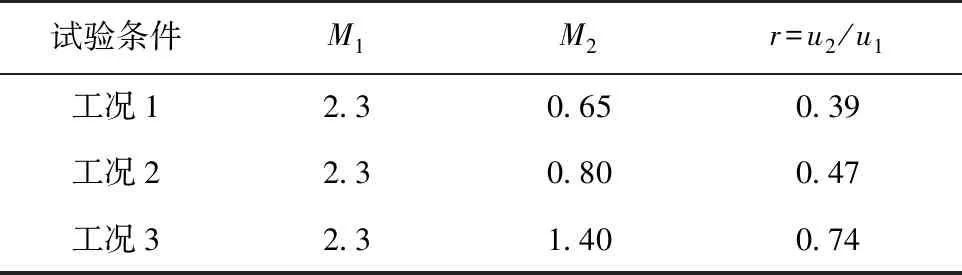
表2 N.Chinzei混合层实验流动参数Tab.2 Inlet flow parameters of the N.Chinzei Experiment

使用上述的LES对混合层进行流场仿真，采用如图2所示的网格对二维混合层流场进行模拟。流场长度L为300mm，宽度H为48mm。流场的网格量为900×150，共包含135000个网格。为了确保能够准确捕捉到交界面涡结构，可将纵向网格节点向上、下来流交界处加密。流场最小网格尺度为5μm。大涡模拟程序中的时间步长可设置为10ns。

图2 混合层流场网格Fig.2 Computational grid for mixing layer

2.2 不同流速比的流场计算结果

采用LES对三种不同流速比的混合层进行数值仿真。待混合层流场完全发展并稳定一段时间后，取同一时刻的三种流速比混合层的流场，计算得到流场沿x方向的涡量云图，如图3所示。

图3 不同流速比混合层涡量图Fig.3 Vorticity maps of mixing layer with different flow field

由图3可以看到，r为0.39的混合层涡结构卷起最快，位置更靠近流场上游；r为0.47的混合层涡结构卷起位置略微靠后；r为0.74的混合层涡结构卷起位置最晚，更靠近下游。同时可以看到，r为0.39的混合层在发展之后出现了涡结构两两之间以及三个之间的配对和融合。由图3可以观察到，混合层流速比越低，同样流向位置处的涡结构之间越容易发生配对与融合。从图3也可以看出，流速比低的混合层在同一流向位置处涡结构的尺寸更大，涡之间的间距也更大。

同样，采用U1-0.1ΔU到U2+0.1ΔU之间的距离来定义混合层的厚度。对同一时间段内的混合层流场厚度进行平均，可以得到不同流速比混合层流场时均的混合层厚度δ，如图4所示。

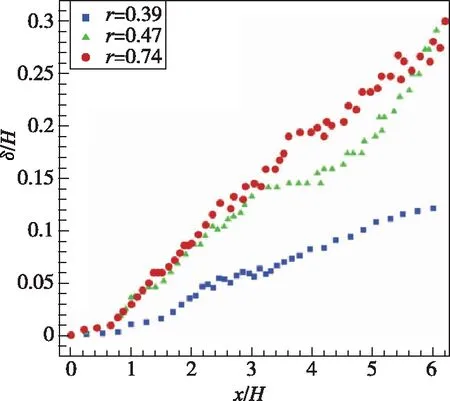
图4 不同流速比混合层厚度Fig.4 Mixing layer thickness of different flow field

从图4可以看出，流速比r为0.47和r为0.39的混合层相对于r为0.74的混合层发展位置更加靠前，这与由瞬时涡结构图所得到的结论一致。r为0.39的混合层在x/H=0.58附近开始快速增长，r为0.74的混合层发展流向位置更加靠后，在x/H=1.62附近才开始快速增长。同时，从图4可以看出，同一流向位置处，流速比高的混合层厚度更大。这一结论与N.Chinzei由实验所得出的结论一致。

3 不同流速比二维混合层气动光学效应

3.1 波面畸变

采用光线追踪方法可以通过模拟光线在介质场中的运动过程，得到平面波穿过流场后的波面畸变。设置所有光粒子均匀分布在y/H=0.5的平面上，所有光粒子射出方向均是沿着y轴负方向竖直穿过混合层到达混合层流场底部(即y/H=-0.5)的平面。每根光线会遇到分布不均匀的流动介质，经过的路径也不相同，因此每根光线具有不同的光程。初始的平面波在经过流场后波面后发生了畸变，变成了扭曲的波面。对r为0.74的混合层在某一时刻的流场采取气动光学仿真，经计算得到OPD，并把同一时刻混合层的涡量云图与OPD线图进行对比，对比结果如图5所示。由图5可以看出，OPD出现的极小值的流向位置与涡结构的涡核中心位置相对应。在图5中，A、B位置单一涡核中心处的OPD均有极小值，类似C处两个以上涡结构相叠加的位置同样对应涡结构的极小值。这是因为对于混合层中的涡结构而言，以涡边界为界限，涡结构内密度均小于涡结构外密度。因此，光线垂直穿过混合层所经过的光程在这种情况下是最小的，即光程差出现了极小值。

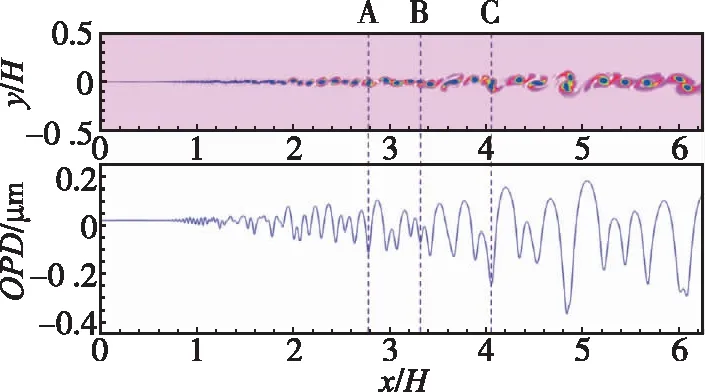
图5 OPD极小值与涡核位置的对应关系Fig.5 Relationship between local minimum of OPD and site of vortex core

取混合层发展完全后的某一时刻的流场，采用光线追踪算法计算OPD。可以看到，r为0.39和r为0.74两种流速比混合层的OPD波面畸变如图6所示。

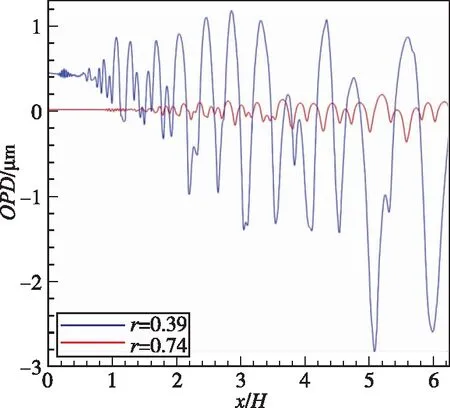
图6 两种流速比混合层OPDFig.6 OPD profile of two mixing layers

从图6可以看出，流速比r为0.74的混合层整体流场的OPD幅值小于流速比r为0.39的混合层整体流场的OPD幅值。这是由于在上下来流介质都是空气的前提下，混合层中涡结构尺度的大小会影响空间的密度分布。可以把涡结构近似看作圆形，涡结构直径越大，光线穿过的涡结构的低密度区域也就越大，此时波面更容易出现大幅度畸变。从图6同样可以看出，涡结构卷起更早的流场，OPD也更早出现波动，这再次印证了OPD与涡结构的对应关系。

3.2 图像偏移

基于光沿直线传播的假设，由于流场网格之间存在折射率的差别，光线在运动过程中以折线方式前进，光线最终出射的位置会出现偏移。基于此，可定义光线经过非均匀复杂流场穿出流场的位置与光线沿着进入流场的初始方向穿出流场出射点之间的距离为图像偏移距离，如图7所示。

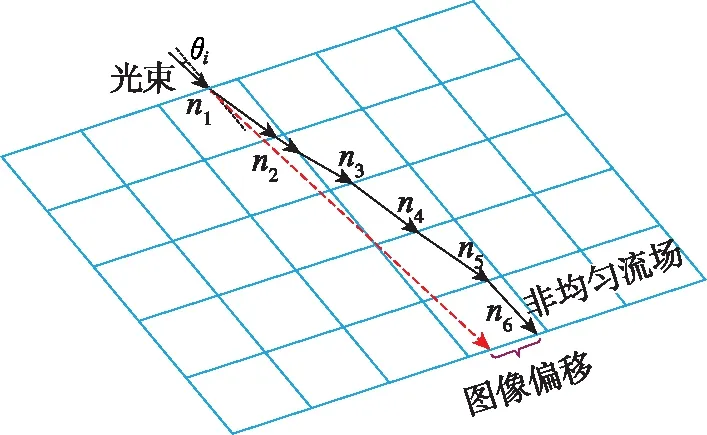
图7 图像偏移示意图Fig.7 Imaging displacement when light is transmitted through the nonuniform flow field

为了方便分析，将混合层流场根据x=0～100mm、x=100mm～200mm、x=200mm～300mm划分为A、B、C三个区段，分别对应混合层流场的上游、中游、下游。光线的入射角θi为0.57°，统计不同流速比的混合层流场在三个区段内所有光线的平均偏移，如图8所示。对于流速比r为0.39和流速比r为0.47的混合层流场，流场中游的图像偏移距离大于流场上游的平均图像偏移，而混合层下游的图像偏移小于混合层中游的平均图像偏移，但仍大于混合层上游的图像偏移。对于流速比r为0.74的混合层，光线穿过混合层的图像偏移沿着流向(上游→中游→下游)依次增大。从图3可以看出，流速比r为0.39和r为0.47的混合层，在涡结构卷起后涡结构变大，光线的图像偏移增大；在x/H=4之后，两个涡结构之间的间距增大。通过涡结构间隙的光线由于折射率相对均匀，几乎不产生光线偏移，因此整个区域的图像偏移相对流场中游更小。对于流速比r为0.74的混合层，混合层的增长速度更慢，涡结构的尺度也增长缓慢，涡间距没有显著的增加，对整个区域的图像偏移没有产生显著的影响。因此，随着流向位置的增加，由大尺度涡结构主导的非均匀折射率场将使图像发生偏移，上游、中游、下游三个区域的图像偏移也将依次增大。

图8 不同流向位置的图像偏移Fig.8 Imaging displacement of different sites of stream wise

3.3 能量衰减

斯特列尔比(Strehl Ratio，SR)是评价气动光学效应的一个十分重要的参数，其定义为受气动光学效应影响的光束强度极值与未受气动光学效应影响的光束强度极值之比[15]，计算公式如下

(5)

式中，OPDrms表示OPD的均方根。斯特列尔比SR也是本文评价气动光学效应严重程度的一个参数。

进行光线追踪的光线波长λ会对SR产生很大影响。以r为0.74的混合层某时刻流场为例，在图9中包含两个正在配对涡结构的区域上方布置光线，光瞳口径为1.44cm，光线沿着y轴负方向入射。

图9 SR计算区域示意图Fig.9 The computational area of SR

为了研究波长对SR的影响，分别取532nm、632nm、1μm、2μm、4μm五种波长。这五种波长包含了从可见光到红外光的典型波长，通过计算可以得到SR随波长的变化，如图10所示。

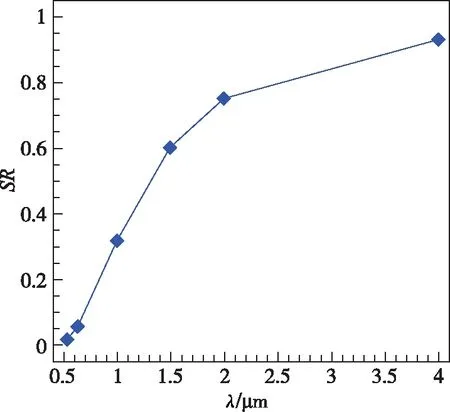
图10 波长变化对SR的影响Fig.10 Effect of wavelength change on SR

由图10可以看到，在给定的流场区域且光瞳尺寸固定的情况下，SR随光线波长的增加而增加。在可见光范围内，SR甚至降低到0.1μm以下。光线波长的减小会使气动光学效应更加严重。在这个混合层流场的算例中，可见光的能量衰减尤其严重。

对于不断发展的混合层而言，涡结构沿着流向是不断发展变化的。在不同流向位置布置光线，SR也会发生变化。针对流速比r为0.74的某时刻混合层流场，沿着整个混合层流场流向一共布置了30个光瞳，取光瞳口径为1cm,光线波长设为2μm。通过光线追踪计算，可以得到SR沿流向的分布，计算结果如图11所示。SR在x/H=2前几乎没有变化，近似等于1，这是由于此时混合层流场还没有开始发展，还没有出现可对气动光学效应产生严重影响的大尺度涡结构。随着混合层的发展，SR发生变化，涡结构卷起后，涡结构和涡之间的间隙交替出现，如前文3.1节所述。当光瞳范围内出现大尺度涡结构时，OPD会出现极小值，SR会明显减小。同时，SR曲线在x/H>2后呈现出逐渐降低的趋势。

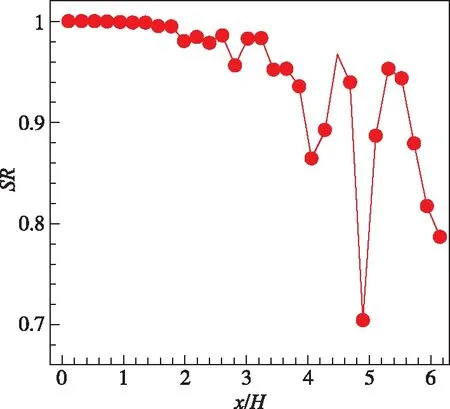
图11 瞬时流场不同流向位置的SRFig.11 SR at different site of stream wise of instantaneous flow field

不同流速比的混合层发展规律不同，对同一时刻混合层完全发展后的三组不同流速比的混合层进行光线追踪计算，并对一段时间内的SR进行时间平均，得到的结果如图12所示。

从图12可以看出，流速比r为0.39和r为0.47的混合层的SR，在x/H>0.8流场出现大尺度涡结构后明显下降；r为0.3的混合层的SR在x/H=2.6时出现了极小值；流速比r为0.39和r为0.47的混合层下游的SR出现了略微增长，这可能与光瞳口径得出选取有关。流速比r为0.47的混合层，在x/H>3.2后基本维持不变，此时SR已衰减为20%，出现严重的气动光学效应。流速比r为0.74的混合层SR在x/H>2后开始降低，在x/H=5.7时衰减至88%。

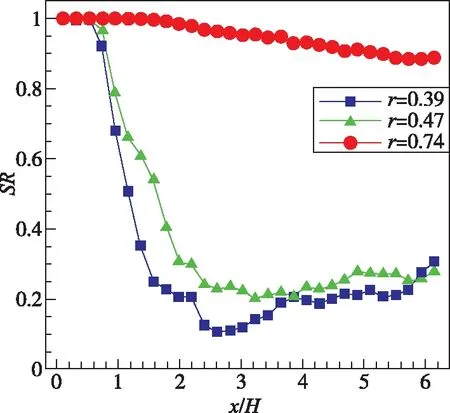
图12 时均流场不同流向位置SRFig.12 SR at different site of stream wise of time-average flow field

4 结 论

本文研究了不同流速比的超声速湍流混合的气动光学效应，应用大涡模拟LES程序对二维混合层流场进行了数值模拟，验证了程序的正确性。开展了不同流速比非定常混合层的数值仿真，并进行了相应的气动光学评价，得出了以下结论：

(1)流速比低的混合层图像偏移更高、更多，SR数值更低。此时，能量衰减严重，气动光学效应更加严重；

(2)针对图像偏移，高流速比的混合层图像偏移沿着流向不断增加。由于涡间距增大，低流速比的混合层的下游图像偏移平均值小于中游图像偏移平均值；

(3)混合层的气动光学效应随着波长减小而愈加严重。可见光的气动光学效应比红外光严重。因此，建议在工程中尽量避免使用短波，以免带来严重的气动光学效应。