基于强化学习的车辆路径规划问题研究
2021-08-12刘虹庆王世民
刘虹庆 王世民
(北京工商大学计算机与信息工程学院 北京 100048)
0 引 言
车辆路径规划问题(Vehicle Routing Problem, VRP)于1959年由Dantzig等[1]提出。该问题定义在一定约束条件下(车载容量、客户需求量、运输过程等)寻求车辆的最优化行车路线,使得运输成本最低或运输距离最短。VRP问题是NP难问题[2],也是运筹学和组合优化领域的研究热点之一[3]。近年来,启发式算法在求解大规模VRP问题中得到广泛的应用和探索。在启发式算法已得到成熟应用的背景下,本文从机器学习的全新角度出发,通过强化学习对车辆路径规划问题进行建模和求解值得探索。本文主要贡献如下:
(1) 为求解小规模的车辆路径规划问题设计了时间差分模型。为减小状态空间过大造成的存储和计算消耗,采用了动态表更新的方法,设计贪婪奖惩机制以加快算法收敛速度,使用Sarsa和Q-learning两个算法进行优化。
(2) 为求解大规模车辆路径规划问题设计了蒙特卡洛模型。借鉴启发式算法的思想,设计了能够有效模仿代理与环境交互的环境模型。使用环境模型采样和蒙特卡洛更新优化代理策略和值函数。
(3) 在小规模算例和大规模算例上分别进行实验,在小规模数据集上对时间差分模型的实验结果及性能进行了分析和对比。同时在大规模数据集上将蒙特卡洛模型和传统启发式算法进行了实验比较和分析。
1 相关工作
求解VRP问题的算法大致可分为精确算法和启发式算法(包括元启发式算法)两类。其中精确算法能得到最优解,但计算复杂高,不适合用于求解大规模的VRP问题。启发式算法又可分为基于邻域的算法和种群法两大类。基于邻域的算法在搜索过程中维持单一解,通过在邻域解之间按策略迭代寻求更优解。该类算法包括迭代局部搜索[4-5]、变邻域搜索[6-8]、禁忌搜索[9-10]、大邻域搜索[11]等。为避免陷入局部最优解,迭代局部搜索引入扰动机制通过扰动当前局部最优解产生新解。变邻域搜索在不同邻域之间切换并进行系统搜索,通过对局部最优解的扰动得到新的搜索起始点。禁忌搜索通过引入禁忌表和相应禁忌准则来避免迂回搜索。大邻域搜索采用破坏与重建的思想扩大邻域搜索空间以得到更优解。种群法则通过模仿生物的群体行为从解空间中寻求优化解,在搜索过程中能同时维持多个解。该类方法包括遗传算法[12-13]、蚁群算法[14-15]、蜂群算法[16-17]、粒子群算法[18-19]、伊藤算法[20-22]等。遗传算法通过模仿自然界的选择与遗传的机理来寻找最优解,是一种具有全局最优性的算法,但遗传算法对初始种群的选择有一定依赖性,且在求解大规模问题时收敛速度慢。蚁群算法、蜂群算法和粒子群算法通过模仿蚁群、蜂群和鸟类的群集智能行为来搜索最优解,有较好的并行性,收敛速度较快。但该类算法的性能依赖于参数的设定,且易陷入局部最优解。伊藤算法通过模仿粒子系统中的粒子相互碰撞与作用的动力学规律来进行算法设计与问题求解。该算法一般与蚁群算法或粒子群算法结合以解决收敛速度慢和局部最优的问题。
强化学习作为除监督学习、非监督学习之外的第三类机器学习方法,近年来受到越来越多的关注和应用。强化学习可以在没有背景知识的情况下通过最大化长期回报来优化代理的行为策略,相比于其他机器学习方法,具有强大的自适应性。强化学习在路径规划任务上已经得到了广泛的应用。文献[23]提出一种监督式强化学习算法以解决强化学习收敛慢的问题。文献[24]提出使用Q-learning解决无人驾驶船舶路径规划问题。文献[25]提出使用势能场知识作为启发信息初始化Q值,以加快算法的收敛速度。文献[26]采用RBF (Radial Basis Function) 网络对Q学习算法的动作值函数进行逼近,并应用于智能车路径规划。文献[27-29]将强化学习方法应用到机器人路径规划研究。
2 模型设计
VRP问题的详细描述可参考文献[1]。令V={v0,v1,…,vnu}表示运输网络节点,其中v0表示配送中心,vi(i≠0)表示第i个客户所在位置,nu表示客户的数量。用d(i,j)表示节点vi到vj的距离,当i=j时,d(i,j)=0。设每辆车的最大载重量为L,第i个客户的货物需求量为qi。强化学习维持一个Q表存储值函数,以表示策略。每轮开始,代理通过当前策略选择一个动作执行并得到环境的反馈,通过反馈更新Q表,如此循环往复,直至收敛。强化学习流程由图1所示。接下来分别介绍小规模问题的时间差分模型和大规模问题的蒙特卡洛模型。

图1 强化学习流程
2.1 小规模问题的时间差分模型
在小规模VRP问题中,将原问题中多个车辆从配送中心出发独立完成配送并回到配送中心转化为等价的单车辆经过多次往返完成配送(即仅有一个代理)的单代理强化学习问题。代理选择下一步动作和代理当前的位置、载重量及各客户的分配状态有关。此时,强化学习的环境应包含以下信息:代理的位置、代理剩余载重量、客户的配送状态。状态可用序列表示,具体地,任一状态s∈S表示为s=(sloc,sload,s1,s2,…,snu)。其中:sloc∈{0,1,…,nu}表示代理在当前s状态下所处的位置,若sloc=i(i≠0),则表示代理当前处在vi客户节点,sloc=0表示代理当前处在配送中心v0;0≤sload≤L是状态s下代理剩余的载重量;si(i=1,2,…,nu)表示第i个客户的配送状态,若客户i在s状态下未被配送,则si=qi,反之,则si=0。
令A(s)表示在状态下代理所有可能的动作,Q(s,a)表示状态动作值函数,作为强化学习优化的目标。代理在当前环境下以一定策略选择一个节点前进,其中a∈{0,1,…,nu}。将贪婪策略记为D(s)1,ε-贪婪策略记为D(s)2。
代理选择一个动作同时会改变环境的状态,将这个过程表示为状态转移函数T(s,a)=s′。状态转移函数涉及到代理位置的变更,载重量的变化,客户分配状态的变化,该过程由算法1描述。
算法1T(s,a)
输入:当前状态s和选择的节点a。
输出:下一状态s′。
1.s′=s;
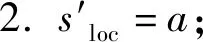
3. ifa=0 then

5. else

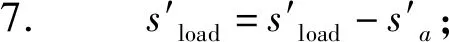
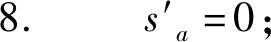
9. end if
10. end if
11. returns′
代理每执行一个动作会通过回报函数R(s,a)得到环境的反馈,以引导代理从试错中学习。为加快算法的收敛速度,在回报函数中引入贪婪奖惩机制,对代理在不同情形下执行的动作给予不同的奖励或惩罚:代理原地不动,则惩罚;代理每执行一次动作给予与其移动距离相当的惩罚;当代理到达一个未配送的客户节点时给予奖励,反之,则惩罚;当代理回到配送中心时完成了整个任务则奖励。回报函数为:
(1)
式中:ρ为一个特定的奖励值,被设定为网络中最长路径段的相反数,即ρ=-max(d(i,j))。
时间差分模型的目标是最大化值函数QD(s,a):
以上模型可通过Sarsa和Q-learning进行单步更新求解,两个算法的更新流程由算法2和算法3给出。
算法2Sarsa
1. 初始化值函数Q(s,a)、episode次数M、初始状态集Sinit⊂S、终止状态集Send⊂S
2. fori=1 toMdo
3. 初始化状态s∈Sinit
4. 使用ε-贪婪策略从s中选择a:a=Dact(s)2
5. repeat
6. Take actiona
7.s′=T(s,a),r′=R(s,a);
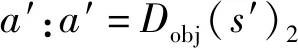
9.Q(s,a)←Q(s,a)+β[r′+αQ(s′,a′)-Q(s,a)];
10.s=s′,a=a′;
1. untils∈Send
12. end for
算法3Q-kearning
1. 初始化值函数Q(s,a) episode次数M、初始状态集Sinit⊂S、终止状态集Send⊂S
2. fori=1 toMdo
3. 初始化状态s∈Sinit
4. repeat
5. 使用ε-贪婪策略从s中选择a:a=Dact(s)2
6. Take actiona
7.s′=T(s,a),r′=R(s,a);

9.Q(s,a)←Q(s,a)+β[r′+αQ(s′,a′)-Q(s,a)];
10.s=s′;
1. untils∈Send
12. end for
同时,考虑到只有少量的状态对于搜索最优解是有用的,采用动态表更新方法。当且仅当代理探索到一个新的状态时,才将该状态加入到状态集合,并在Q表中增加该状态的记录。这样可以避免由于状态空间过大带来的存储空间和计算资源的消耗。
2.2 大规模问题的蒙特卡洛模型
由于状态空间随客户点数量增加呈指数级增长,时间差分模型求解大规模VRP问题变得不实际。可通过构建模型,通过采样模拟代理和环境的交互求解大规模问题:(1) 将可行解分解为多条以配送中心为起点和终点的路径集合,记为H;(2) 最优解必定包含在所有可能的H的集合中;(3) 通过蒙特卡洛法搜索最优解,结合启发式算法思想加快搜索速度。将H中的路径记为h,长度记为d(h),则问题的目标是从找到路径长度之和最小的H,即:
强化学习求解大规模VRP问题选择合适的环境模型值得进一步研究。本文在环境模型中使用了启发式函数,可在算法迭代过程中优化策略的同时不断优化环境模型。将环境模型记为E,由算法4描述。
算法4环境模型E
1. 初始化未访客户集U={1,2,…,nu}、解集H={}、S状态代理剩余载重量sload=L
2. repeat
3. ifU∅ then
4. 初始化一条子路径h=(0)
5. 从U中随机选择一节点a
6.sload=sload-qa;
7. 将a加至子路径h
8. 从U中移除a
9. repeat

11. ifsload≥qathen
12.sload=sload-qa;
13. 将a加至子路径h
14. 从U中移除a
15. else
16. break
17. end if
18. until
19. 将0添加至子路径h
20. 将0添加至子解集H
21. end if
22. until
23. returnH


(2)
令hsa表示从s到a的直连路径,则式(2)中(s,a)表示路径中含有hsa的所有H的集合,QD(s,a)表示在D策略下代理从s位置移动到a位置的值函数。策略D借鉴启发式算法的思想,将s状态下选择动作a的概率定义为:
(3)
式中:λ和μ是模型的参数。λ控制模型的全局性,λ越大,则代理以越大的概率选择当前Q(s,a)最大的动作执行。μ控制了模型的局部性,μ越大,则由d(s,a)引入的局部差异越大,模型偏向于更随机地做出决策。
蒙特卡洛法从环境模型中采样得到一组序列,其中有个序列含路径段hsa,记为{H1,H2,…,Hw}。将值函数中的期望用均值近似,则有:
(4)
i=1,2,…,W
在实际计算时,使用一个计数表记录所有的在采样中出现过的次数,将W用C(s,a)替代,并且每采样一个序列便更新相应的值函数QW(s,a)。蒙特卡洛模型(MCRL)由算法5描述。
算法5MCRL
1. 初始化值函数Q(s,a)=Qinit(s,a)、计数表C(s,a)=0、M、每一采样时间的序列数量W
2. fori=1 toMdo
4. forj=1 toWdo
5. 使用环境模型E采样一个episodeH

7. end for

9. for eachhinHdo
10. for each pair (s,a) inhdo
11.C(s,a)=C(s,a)+1;
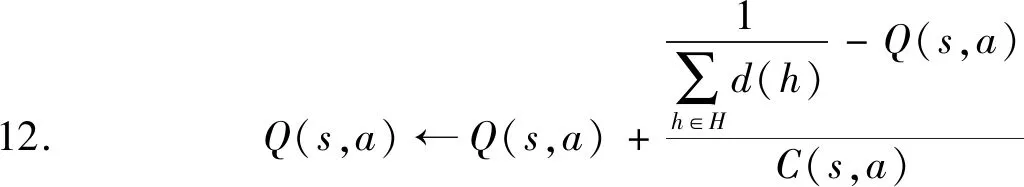
13. end for
14. end for
15. end for
16. end for
3 仿真实验与分析
实验环境为Windows 10 64位操作系统, Intel Core i5 处理器,8 GB RAM,实验工具为Python 3.6。
3.1 小规模问题仿真实验
小规模问题仿真实验选用文献[34-37]的仿真数据样例,该样例包含8个客户,配送中心有2辆车, 每辆的最大载重量为8吨,具体信息可参考文献[30]。该问题已知最优解的路径长度为67.5。Sarsa和Q-learning算法的实验结果如图2所示。

图2 Q-learning和Sarsa不同参数设定对比图
Q-learning和Sarsa均未使用环境模型,在优化的前期阶段解,选择动作的随机性较强。Q-learning随着更新轮数的增加,解的路径长度下降速度相对于Sarsa快,展现了时间差分法优化速度快的特点和异步策略更新的优势。当ε较大时,Q-learning更多地选择随机策略以探索可能的更优解,加快了收敛速度。但当ε过大时,算法对现有的最优解利用较少,随机性过大大,算法将难以收敛到最优解。强化学习算法在合适的ε下具有近似的全局最优性,可避免在启发式算法中容易出现的局部最优问题。
3.2 大规模问题仿真实验
大规模问题选用文献[34]中标准CVRP实例库Set A中的算例进行测试。将MCRL算法和遗传算法(GA)、粒子群算法(PSO)及蚁群算法(ACO)在不同测试数据下的结果进行对比,其中:GA[35]、PSO[39]的结果来源于文献[31],ACO使用文献[36]的LNS-ACO算法的结果。各算法得到的最优解由表1给出。

表1 大规模问题实验对比表
可以看出,MCR算法在A-n32-k5、A-n33-k5、A-n34-k5、A-n39-k6、A-n44-k6及A-n46-k7算例上都能达到最优解。在A-n60-k9和A-n80-k10算例上,MCRL算法的最优解均超过了GA和PSO,与LNS-ACO算法的最优解相当。MCRL算法结合了强化学习交互式学习的特性和启发式函数快速收敛的优点,既能保证强化学习在大规模VRP问题上的有效应用,又能提高模型的容错率、可扩展性和可交互性。同时,将强化学习和启发式函数相结合的方法可应用在更多的规划问题和组合优化问题中,相比于单纯的启发式算法有更广的应用范围。
4 结 语
引入强化学习研究车辆路径规划问题。从不同的问题规模出发,设计了使用Sarsa和Q-learning算法求解小规模问题的方法和使用蒙特卡洛模型求解大规模问题的方法。通过实验测试了两类方法在求解不同规模的VRP问题下的表现,并和现有的启发式算法进行了对比,验证了强化学习求解VRP问题的有效性,为研究车辆路径规划问题及相似的组合优化问题提供了新的思路。将强化学习的方法结合启发式算法可以有效利用强化学习交互性学习的特性和启发式算法快速收敛的优势。下一步工作可考虑使用函数近似的方法代替表更新的方法,例如,通过引入神经网络近似值函数,以梯度下降的方法更新网络参数,以应对状态空间过大的问题。
