基于强社交图的多约束信任图模式增量匹配算法
2021-08-12王钰蓉丁鹏飞
王钰蓉 丁鹏飞 刘 安
(苏州大学计算机科学与技术学院 江苏 苏州 215006)
0 引 言
图模式匹配(GPM)在许多基于社交网络的应用中发挥了重要的作用,如专家发现[1]和社交社区挖掘[2]。GPM通常是根据子图同构来定义的,其中模式图和数据图之间需要节点和边的精确匹配。子图同构是一个经典的NP完全问题,计算量大。此外,对于一些社交应用程序来说,点和边的精确匹配过于严格。因此,提出了图模拟[3]的概念。在图模拟中,如果数据图中路径的起点和终点分别与模式图中的边的两顶点具有相同的标签,则该路径被视为模式边的匹配。然而,对于一些实际应用而言,图模拟有时仍然过于严格[4-5]。然后,提出了有界模拟[6]的概念。在有界模拟中,每个顶点都被标记为特定的类别,每个边都可以用常数k或*标记。k和*分别代表匹配的最大路径长度的约束不大于k以及不限制该路径长度。有界模拟不执行边到边的映射,而是通过有界长度将模式图中的边与数据图中的路径匹配[6]。根据有界模拟的性质,基于有界模拟的GPM试图找到最小直径的子图。
然而,上下文社交网络中[7]具有许多与顶点和边相关联的上下文信息,例如特定领域中用户的社会角色(例如,AI的顶级专家),以及用户之间的社会关系(例如,同事关系)和用户之间的信任度。在基于社交网络的各种应用中,如众包旅游[8]、研究团队选择(classroomsalon.com)和社交网络中的专家发现[7],人们通常愿意对GPM中用户之间的亲密社交关系和用户之间的强信任关系设置一些约束。这些因素对用户的决策和协作有显著影响[9-12]。
因此,在基于GPM的社交图应用中,一种带有有界路径长度和社交上下文多重约束的图模拟方法具有重要意义。基于同构的GPM、图模拟和有界模拟之间的关系如图1所示。具有多个约束的GPM覆盖了NP完全的多约束路径问题[13-14]。因此,在基于多约束模拟的GPM中采用传统的算法进行有界模拟计算代价昂贵。这是因为传统的GPM算法必须枚举每个约束的所有可能匹配,然后找到匹配的区间,导致效率低下。此外,现有的正则路径查询方法[15-16]只考虑了一个表达式,没有考虑到不同属性的多正则表达式,因此正则路径查询方法不适用于基于多约束模拟的GPM。在以前的研究基础上[17-18],本文提出了一个考虑多约束的近似算法。这些方法在求解MC-GPM问题中证明了其有效性和效率。
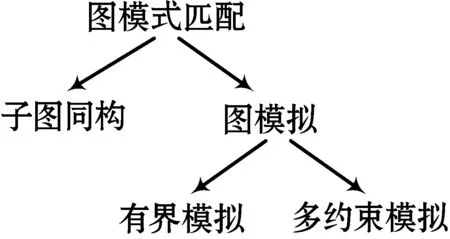
图1 图匹配方法分类
在实际应用中,在线社交网络会频繁地改变。例如,在Facebook上,平均每分钟有400个新用户加入,这会导致社交图结构的变化。一家市场研究公司Statista(statista.com)已经表明了这种频繁变化的存在。但是现有的工作没有提供多约束下的增量匹配,导致GPM在面对数据图结构的变化时效率较低。因此,目前面临的主要挑战是设计高效的技术来支持MC-GPM查询。本文的主要工作包括:
(1) 提出了一个新的概念,称为强社交图(SSG),它是由具有强社会关系的用户组成的网络结构,并提出了一种识别SSG的方法以及一种新的具有多项式时间复杂度的SSG索引结构。
(2) 提出了一种SSG索引增量维护算法INC-SSG。当面临SSG结构的变化时,INC-SSG可以根据受影响的小部分SSG来更新SSG索引,而不是通过扫描整个SSG结构来重建SSG索引,这可以大大节省MC-GPM的查询处理时间。
(3) 在INC-SSG的基础上,提出了一种强社交图增量MC-GPM算法SSG-IncMGPM。它可以在原匹配结果上进行增量计算,避免重新查询匹配,加速结果查询。
(4) 对五个大规模的真实社交图进行了广泛的实证研究,验证了本文所提出的SSG-IncMGPM算法的有效性和效率比现有最好算法SSG-MGPM[19]在回答MC-GPM查询时的优越性。
1 相关工作
为了减少GPM的同构复杂度,Zou等[20]提出了一种索引方法来记录数据图中任意两个节点之间的最短路径长度。该索引可以加快GPM的进程。Sun等[21]提出了一种图模式匹配方法,避免了建立整个图的索引,从而减少了查询处理时间。此外,Cheng等[22]提出了一个索引,用于记录两跳范围内的顶点,以加快GPM过程。Cheng等[23]提出了一种Top-k查询优化方法,建立了循环图查询的生成树,并根据答案边的长度之和对答案进行排序。Ren等[24]提出了一种缓存多个查询图并重新排序这些查询序列的方法,以提高查询的应答效率。在实际应用中,从同构的角度提取包含整个查询图的子图通常是不现实的。因此,Yan等[25]定义了一个距离来研究查询图和数据图之间最大公共子图中匹配的差异。它们为距离的上限定义了一个阈值,距离在上限内的子图就是需要的结果。Zhu等[26]将一个数据图分成若干组相似的图,并对这些图进行索引,以支持有效的剪枝,从而提高基于相似性的GPM的效率。此外,Shang等[27]提出了一种索引方法来索引查询图和数据图中特征的相似性,以提高GPM的效率。为了进一步提高大图中图模式匹配的效率,文献中提出了采用分布式并行GPM方法进行图模式匹配的研究。Shao等[28]在一个大数据图中采用并行框架提取匹配子图。此外,文献[29-30]的研究提出了将大数据图分解成小数据图的方法,通过将小数据图的每个分区的结果连接起来,可以得到图模式匹配的结果。此外,Huang等[31]还提出了一种将大数据图分解成若干小片段的方法。
由于子图同构方面的GPM在某些实际应用中过于严格,为了进一步放宽约束,图模拟[32]和有界模拟[6]应运而生。图模拟可以避免精确的点对点匹配,是在模式图和数据图中匹配两个节点的标签。在有界模拟中,没有精确的边到边匹配的限制,而是指定了数据图中匹配路径的最大路径长度。这种GPM可以在立方时间内进行。有界模拟[33]是图模拟的一个扩展,它进一步考虑了GPM中不同类型边的需求,并根据有界模拟[1]开发了一个社会专家查找系统。Sun等基于图模拟,研究了特定点匹配问题[34-35]。Fan等[36]进一步提高了基于有界模拟的GPM的效率。他们从数据图中提取一组视图,然后研究这些视图是否能够回答特定GPM的有界模拟。在分析视图的基础上,Fan等[37]又提出了一个资源有界查询。在他们的模型中,数据图只有某些部分被识别和索引,因为这些部分很可能包含一些典型模式图的答案。文献[17]提出的工作考虑了社交背景的多重约束,但没有提供增量更新索引的场景,导致GPM在面对数据图结构变化时效率低下。
2 强社交图与基于强社交图的索引
2.1 强社交网络
图论[38]中定义了强连通概念:当一个图任意两个顶点都是可达的,则这个图称为强连通图。强连通分量可以是有向图中强连通的子图。基于图论中强连通的定义可以延伸出强社交图的概念:如果每个顶点的角色影响力值都很高,并且顶点之间相连接的边都具有亲密的社交关系和强社交信任关系,则这种连接称为强社交连接,这种子图称为强社交图(SSG)。强社交图的细节可以在文献[18]中找到,发现SSG的伪代码如算法1所示。
算法1SSG发现算法
输入:数据图G,k,λV,λE
输出:SSGi(i∈[1,k])
1) Selectvii∈[1,k],LV(vi)>λV;
2) Setvi.visit=0;
3) PutviintoExpSet;
4)WhileExpSet≠∅do
5) GetvifromExpSet;
6) RemovevifromExpSet;
7)Ifvi.visit=0then
8) Setvi.visit=1;
9)Foreachvj(vjis a neighbor ofvi)do
10)IfLV(vj)>λVandLE(vi,vj)>λEthen
11) PutvjintoExpSet;
12) AddvjandE(vi,vj) into SSG;
正如社会科学研究[39]所指出的,SSG的结构和相应的社交情境,包括用户之间的信任、用户之间的社交关系以及用户的社会角色可以在很长的一段时间内保持稳定。
因此,可以建立SSG的索引来加速MC-GPM。识别所有SSG也是NP完全问题,因为它覆盖了经典NP完全最大团问题[38]。因此,可以随机选择具有高角色影响因子值的k个顶点来作为k个种子。然后采用广度优先搜索方法识别出k个SSG,找到与种子有密切社会关系和强信任关系的顶点。建立SSG的时间复杂度为O(NDED)。
2.2 强社交图索引
为SSG建立一个索引结构,如图2所示。表1是辅助索引构建的矩阵,矩阵中记录了两点间的最短距离及相应路径。在这个索引中,索引了3种信息:可达性、图模式和社交背景。

图2 SSG索引结构
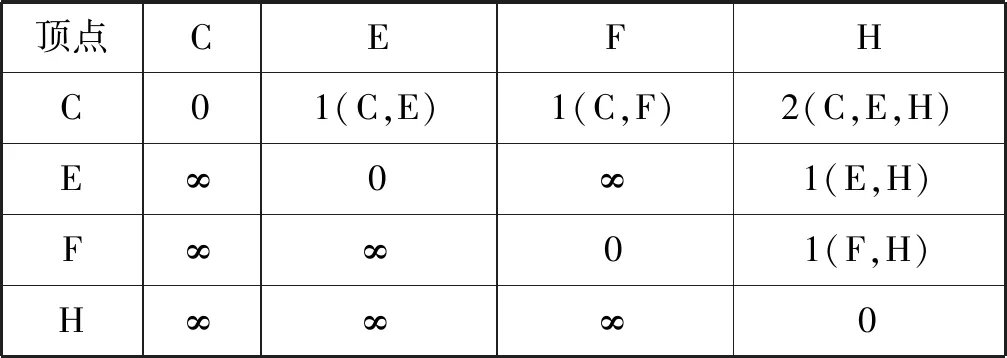
表1 SSG索引矩阵
(1) 可达性索引。首先建立可达性索引,记录节点间的可达性关系。在每个节点上,它都会保存一个列表来索引节点的祖先和后代。因为SSG的大小通常比整个数据图小很多,可以有效地建立可达性索引[40]。然后,在执行MC-GPM时,可以有效地检查SSG中任意两个节点之间是否可达。
(2) 图模式索引。建立可达性索引后,再建立图模式索引,记录SSG的图模式信息。记录SSG中任意两个节点之间的最短路径长度。然后,在执行MC-GPM时,可以有效地检查匹配的路径长度是否满足SSG中有界路径长度的约束。
(3) 社交背景索引。基于可达性索引和图模式索引,建立了社交背景索引。该索引是记录SSG中路径的聚合社交影响因子的最大值。在执行MC-GPM时,可以有效地检查聚合的社交影响因子值是否满足SSG中用户给定的约束:如果两个顶点之间的一条路径的T、r和ρ的聚合值均占主导地位,将该路径长度和相应的聚合社交影响因子值作为索引。否则,索引最多三个路径,分别具有最大聚合T、r和ρ值。
索引中记录了SSG中的重要信息。给定一个MC-GPM查询,如果查询边的两个顶点可映射到SSG中的一条路径中,则该索引信息可用于快速查找是否存在边模式匹配,从而大大节省查询处理时间。此外,在最坏的情况下,需要执行Dijkstra算法4次,因此构造索引的时间复杂度为O(NDlogND+ED)。
3 SSG索引的增量维护算法INC-SSG
3.1 INC-SSG问题
表2中给出了本文中使用的相关符号及其含义。

表2 符号表

续表2
INC-SSG问题的定义如下:
输入:强社交图SSG、SSG索引、矩阵M和SSG的变化。
输出:更新的SSG索引。
定义1当面对SSG的变化时,INC-SSG是通过查找SSG受影响的部分AFF来增量更新SSG索引信息。
3.2 算法概述
上述可达性、图模式和社交背景索引可有效地用于研究是否存在图模式匹配。然而,在实际应用中,图的结构变化是常见的[41],每次更新图时重建整个索引结构的成本太高。这促使需要研究增量方法来最大限度地保持旧索引,只更新受影响的部分索引,而不是重建整个索引结构。因为图的结构变化在实践中通常很小,所以受影响的索引与整个索引相比所占比例也很小。例如,2017年6月,Facebook每月活跃用户超过20亿,每个月约有60万新用户加入,但仅占所有用户的0.03%。显然,更新受影响部分的索引比更新整个图更有效。只需构建一次图的完整索引,然后更新图时只要增量地维护索引。根据初始可达性索引和图模式索引计算影响区域,用矩阵来记录这些信息。
3.3 单边删除的索引更新算法
首先给出一个处理单边删除的增量算法,用ED-SSG表示,具体如表3所示。

表3 删除边(C,E)后的索引矩阵
算法2单边删除更新索引的算法
输入:SSG,SSG索引,删除的边(v,w),矩阵M。
输出:更新的索引。
1) 初始化:AFF=∅;
2)Foreach vertexzin SSG andz≠vdo
3)Ifz∈Des(v) andpath(v→z) containswthen
4) addvtoaffectedVertices(z);
5) add(v,z) toAFF;
6)Foreach vertexu∈Anc(v)do
7)Ifpath(u→z) containsvthen
8) addutoaffectedVertices(z);
9) add (u,z) toAFF;
10)Foreach pair(u′,u″) inAFFdo
11)Foreach vertexa∈Des(u′)do
12)Ifa∉affectedVertices(u′),u″∈Des(a),a≠w
andpath(u′→a),path(a→u″) do not contain
the vertexwthen
13)M(u′,u″)=min{Slen(u′,a)+Slen(a,u″)}∪{∅};
14)path(u′→u″)=path((u′→a)+path(a→u″);
15)Foreach pair(u′,u″) inAFFdo
16)IfM(u′,u″)=∞then
17) removeu″ from the indices ofu′;
18) removeu′ from the indices ofu″;
19)Else
20)Slen(u′,u″)=M(u′,u″)=Plen(u′,u″);
21) computeASaccording to thepath(u′→u″);
22)Returnthe indices of SSG;
步骤1将AFF初始化为空。AFF是节点对集合,记录图更新时节点间距离发生变化的节点对。
步骤2对于SSG中的每个顶点z(v除外),查找到z的最短路径长度受影响的顶点。如果z是v的后代,且从v到z的最短路径经过w,则删除的边(v,w)会影响v和z之间的距离。然后,搜索v的祖先,以找到到z的最短路径经过v的顶点。否则,这意味着删除的边不会影响任何其他顶点与z之间的距离,因此继续搜索图中其他未探索的顶点。
步骤3根据AFF更新矩阵M。对于AFF中的任何节点对(u′,u″),如果存在一个顶点a,它是u′的后代,u″是a的后代且(a,u′)不在AFF中。此外,a满足u′到a和a到u″的最短路径都不经过w,然后计算u′到u″经过a的最短路径长度并记录路径。否则,继续调查AFF中的另一个节点对。
步骤4根据矩阵M和AFF更新索引。当u′与u″之间的距离为∞时,u″应从u′的可达性索引、图模式索引和社交背景索引中去除。同样,u′也应该从u″的索引中去掉。否则,更新u′和u″的图模式索引和社交背景索引。Slen的值等于新的最短路径长度。根据记录的路径,重新计算Plen和AS。
步骤5返回新SSG的更新索引。
例1:如图3所示,给出了一个SSG,删除边(C,E)。

图3 删除边(C,E)后的索引结构
更新索引的步骤如下:
(1) 找到矩阵M受影响的部分,并以顶点E为例。E是C的后代,C到E的最短路径通过E,从而C和E之间的距离受到影响。类似地,研究其他顶点H和F。最后,受影响的节点对是(C,E)和(C,H)。
(2) 更新矩阵M。C和E之间的距离变为∞。C与H的距离仍为2,但最短路径为C→F→H。
(3) 顶点C和E将分别从E和C的索引中移除。AS的值应重新计算为AS(path(C→H))={0.86,0.81,0.89}。
复杂度:算法的伪码在算法2中给出。复杂度是O(n),其中n是SSG中顶点的数目。
3.4 单边插入的索引更新算法
同样,也设计了一个增量算法来处理单边插入,用EI-SSG表示,具体如表4所示。
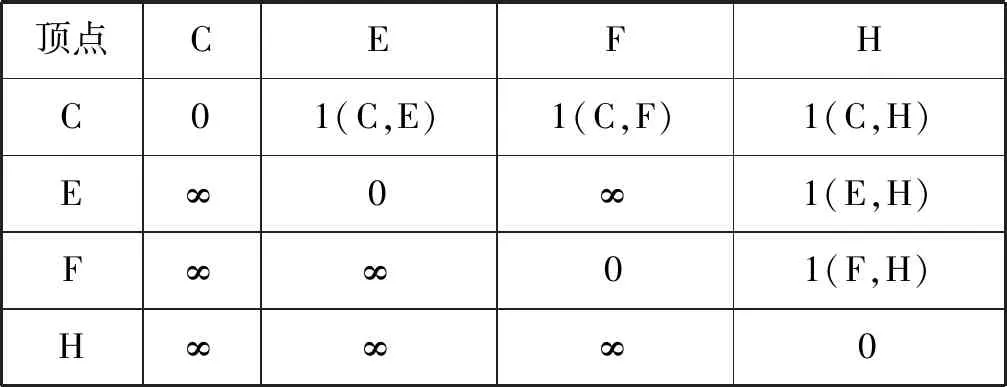
表4 插入边(C,H)后的索引矩阵
算法3单边插入更新索引的方法
输入:SSG,SSG索引,插入的边(v,w),矩阵M。
输出:更新的索引。
1) 初始化AFF:∅;workSet:{(v,w) };visitedVerteices:{v};
2)Foreach vertexzin SSG andz≠vdo
3)WhileworkSetis not emptydo
4) get and remove edge (u,u′) fromworkSet;
5)IfM(u′,z)>0 andM(u′,z)≠∞then
6)dist(u,z)=Slen(u,z)∪{∞};
7)dist(u′,z)=Slen(u′,z)∪{0};
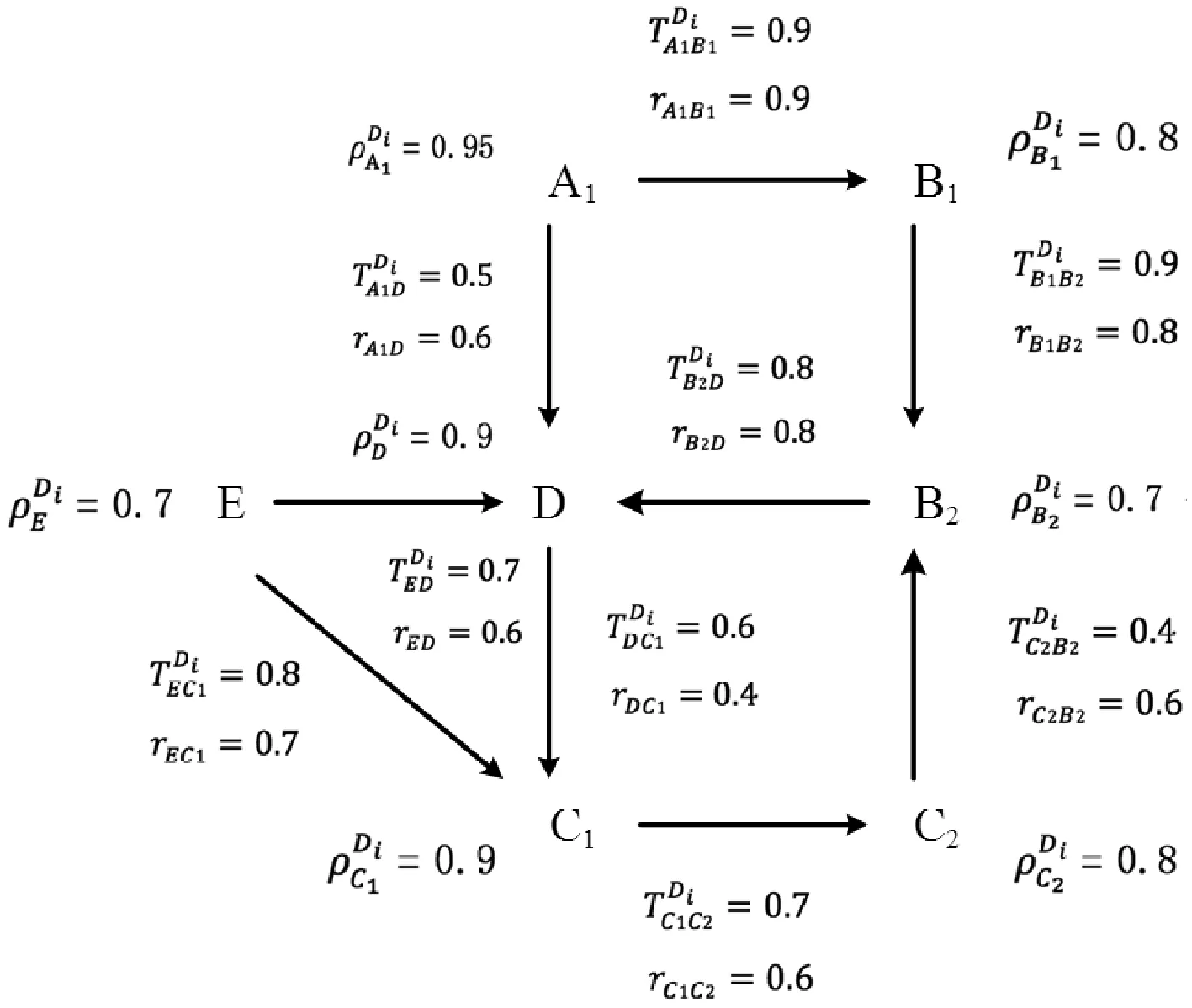
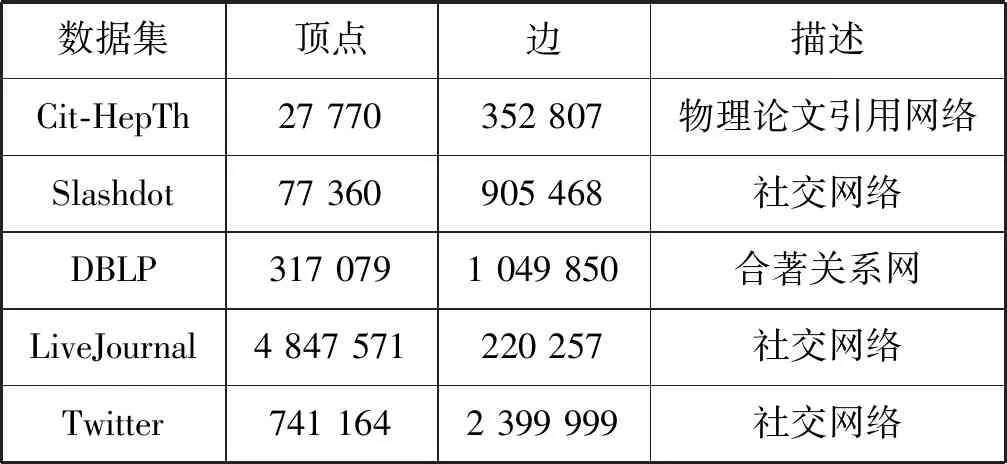
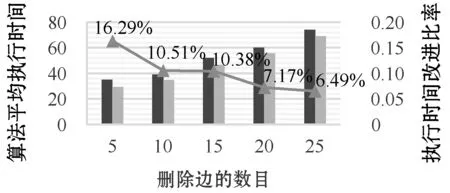
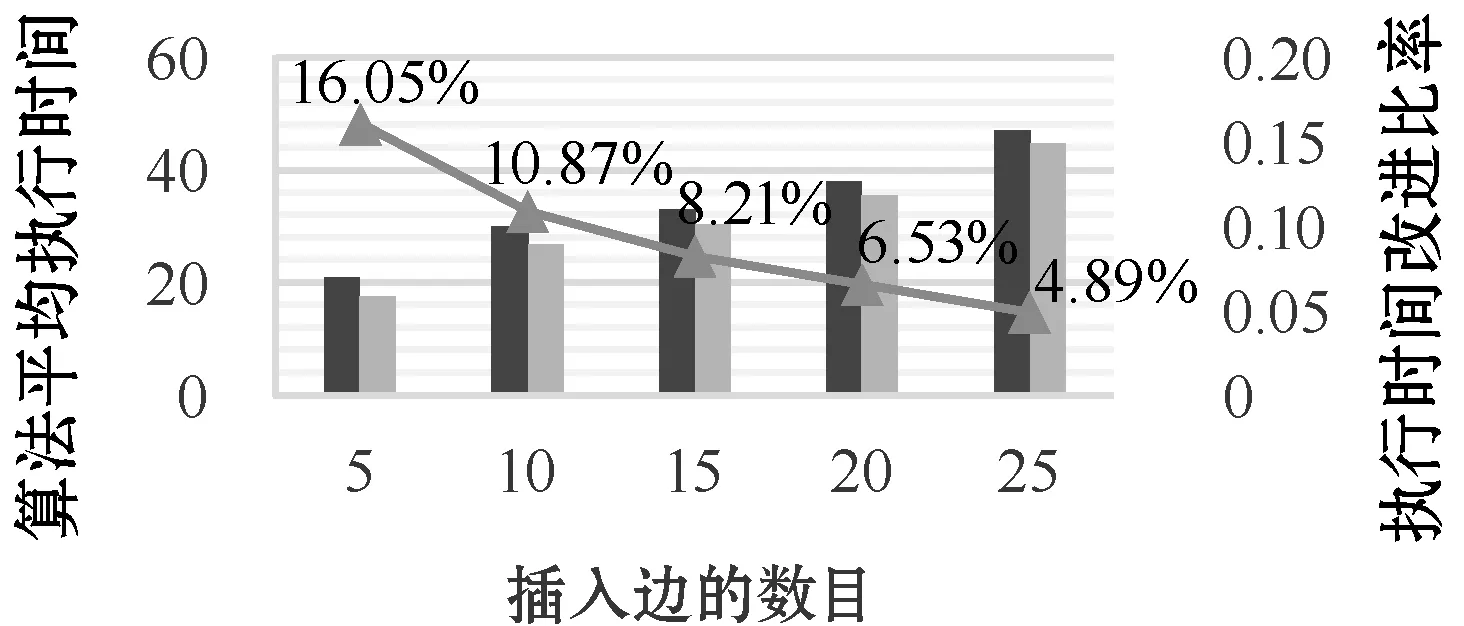
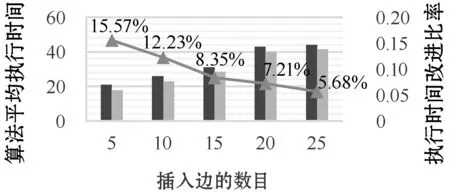
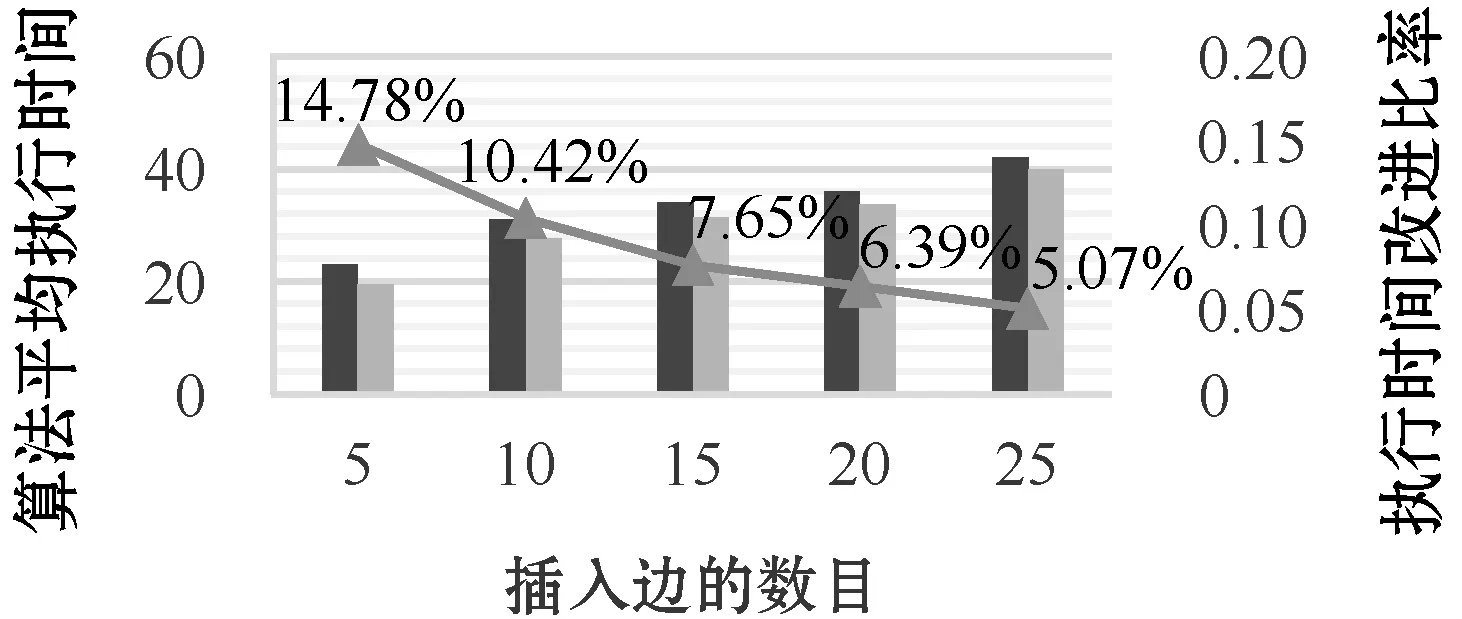
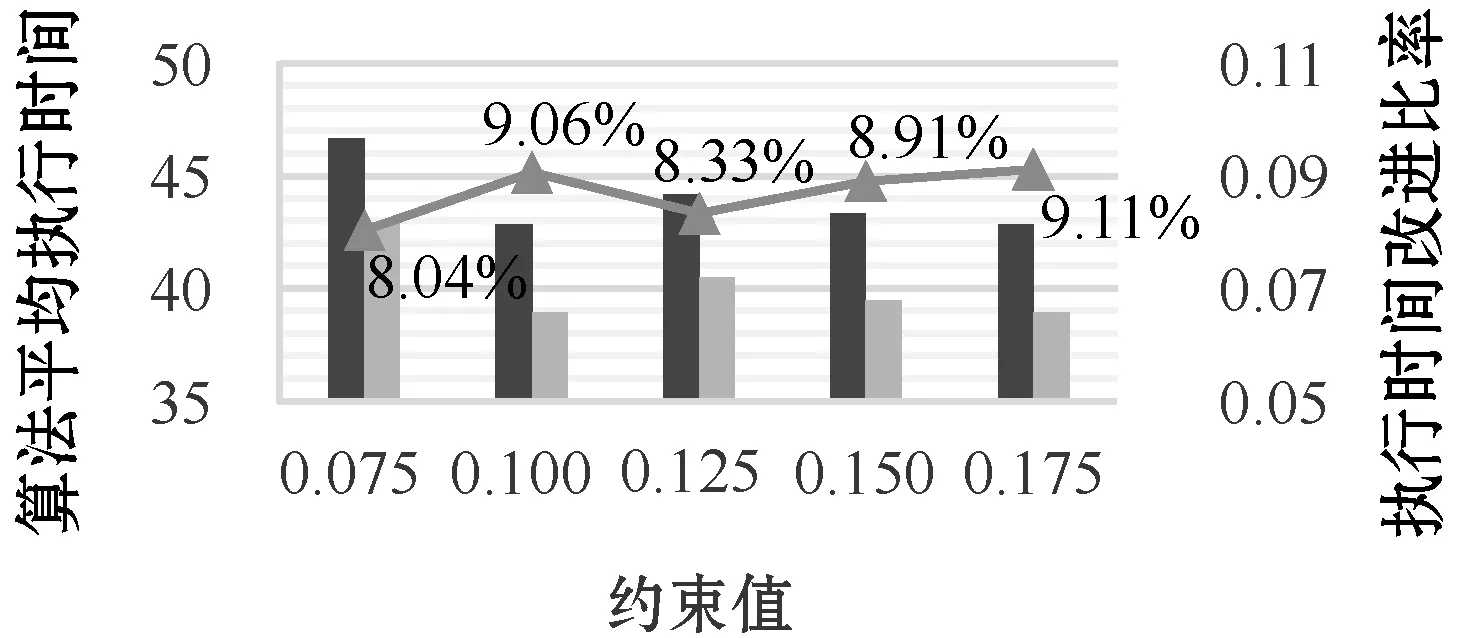
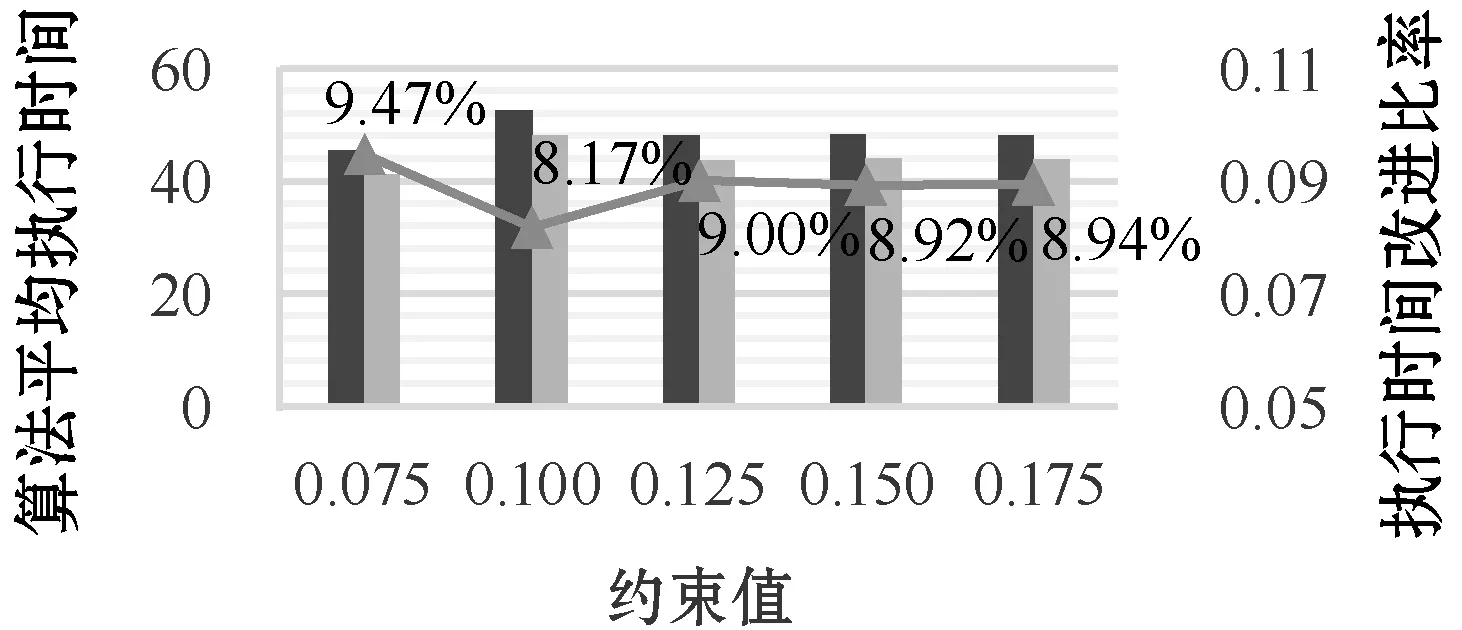
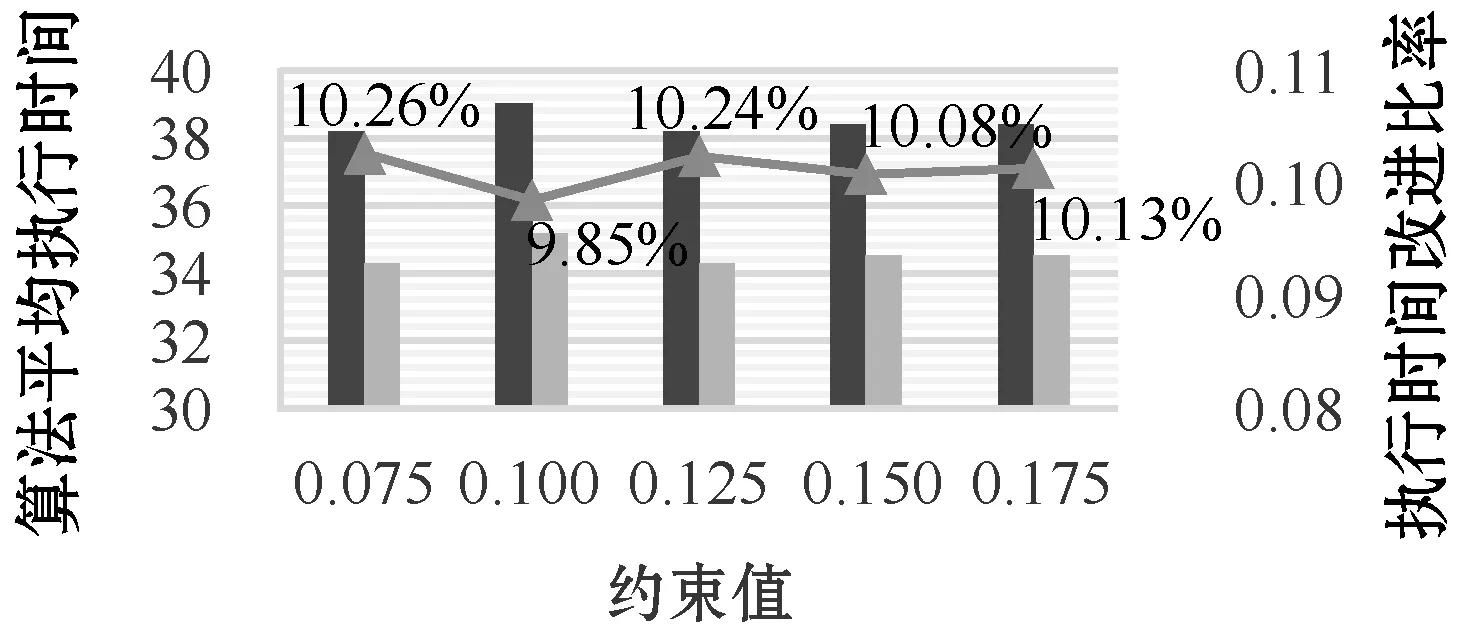
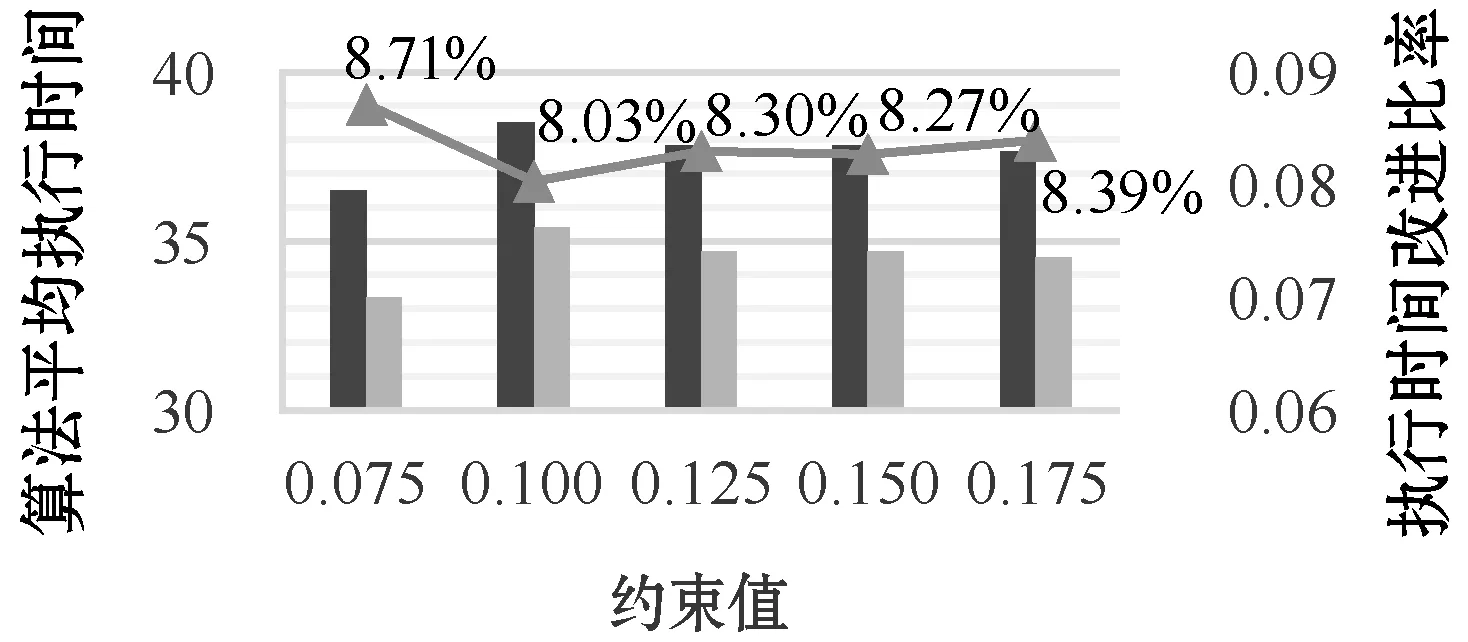
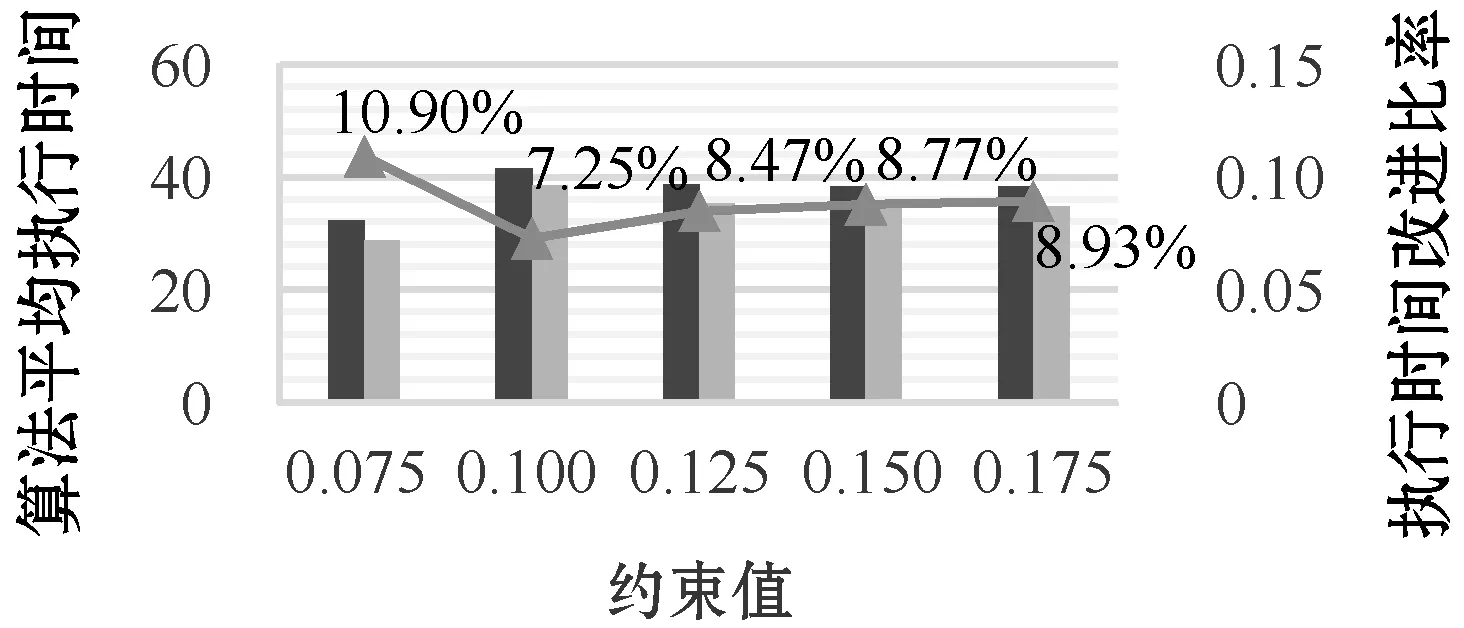
8)If(1+dist(u′,z)) 9) add (u,z) toAFF; 10)M(u,z)=1+dist(u′,z); 11)path(u→z)={u}+path(u′→z); 12)Foreachv′∈Anc(u),Slen(v′,u)=1 andv′ is not invisitedVerticesdo 13)Ifpath(v′→z) containsuorM(v′,z)=∞ then 14) addv′ tovisitedVertices; 15) add (v′,u) toworkSet; 16)Foreach pair (vf,vt) inAFFdo 17)Ifvtis not inDes(vf)then 18) addvttoDes(vf),Slen=M(vf,vt)=Plen; 19) computeASaccording topath(vf→vt); 20) addvftoAnc(vt),Slen=M(vf,vt)=Plen; 21) computeASaccording topath(vf→vt); 22)Else 23)Slen(vf,vt)=M(vf,vt)=Plen(vf,vt); 24) computeASaccording to thepath(vf→vt); 25)Returnthe indices of SSC; 步骤1将AFF初始化为空,将(v,w)添加到workSet,将v添加到visitedVertices。 步骤2对于SSG中的每个顶点z(v除外),重复执行步骤3,直到workSet变为空。 步骤3计算AFF,同时更新矩阵M。从workSet中获取并移除(u,u′)。如果u′到z是可达的,计算u和z之间的新距离,并将其与旧距离进行比较。如果新距离更好,则更新矩阵M并在从u′到z的路径首部添加u。此外,将(u,z)添加到AFF。然后,转步骤4。否则,重复执行步骤3。 步骤4找到u的祖先v′,如果从v′到z不可达,或者从v到z的路径通过u,则将(v′,u)添加到workSet,并将v′设置为已访问。否则,继续调查u其他未被访问过的祖先。 步骤5根据矩阵M和AFF更新索引。对于AFF中的任何节点对(vf,vt),如果在更新前vt不是vf的后代,则应将vt、vf分别插入vf和vt的索引中。同时根据记录的路径计算Slen、Plen和AS。否则,更新vf和vt的图模式索引和社交背景索引。Slen的值等于新的最短路径长度。根据记录的路径,重新计算Plen和AS。 步骤6返回新SSG的更新索引。 例2:如图4所示,SSG中插入边(C,H)。 图4 插入边(C,H)后的索引结构 索引更新步骤如下: 首先,找到AFF并同时更新矩阵M,取顶点H为例。C和H之间的距离变为1,比原距离2更近。因此,更新M并记录路径C→H。显然,顶点C没有任何祖先,因此继续研究E和H。最后,受影响的节点对是(C,H)。 接下来,更新索引。C和H之间的最短路径长度变为1。重新计算AS(path(C→H))={0.98,0.9,0.92}。 复杂度:算法的伪码在算法3中给出。复杂度是O(n|E|),其中n是SSG中顶点的数目,而|E|是SSG中的边数。 在上述算法的基础上,更容易解决顶点更新问题。接下来,给出处理顶点删除和插入的简明说明。 顶点删除:给定一个删除的顶点v,首先根据可达性索引求出从v开始或结束于v的边。对于每个受影响的边,执行前面提到的算法ED-SSG。更重要的是,不要忘记从矩阵中删除v对应的行和列,同时删除v的索引。该算法被称为VD-SSG,删除每条边的复杂度是O(n)。 顶点插入:处理顶点插入的算法由VI-SSG表示。与顶点删除相反,首先需要将顶点v′的行和列插入到矩阵中。然后,通过算法EI-SSG处理相关的边。类似地,插入每条边的复杂度是O(n|E|)。 提出的INC-SSG算法可以应用于整个社交图。然而,在大规模的社交图中,建立和维护索引信息可能会导致昂贵的时间开销,其中图结构和属性值的更改比SSG中的更改更频繁。此外,在图模式匹配过程中,数据图中的许多节点不会被访问,而强社交图中节点访问概率更高。因此,保留整个社交图的索引信息是没有必要的。 首先,采用HAMC方法[17]对原始数据图进行查询图匹配,获得初始匹配结果。HAMC方法是现今解决未发生图结构变化的MC-GPM问题最优的方法。然后,当数据图更新时,采用INC-SSG对索引进行更新。最后,调用增量匹配算法IncGMPM对初始匹配结果进行增量计算,得到最终匹配。下面介绍多约束路径匹配的一个目标函数,用来辅助匹配过程;其次,对增量匹配算法进行详细说明,如图5所示。 图5 增量匹配算法框架SSG-IncMGPM 首先,对于强社交多约束信任图中的路径匹配问题,给出一个目标函数式如下: (1) 在对更新之后的数据图进行图匹配时,因为每次更新操作量都是相对较少的,若每次更新都要重新匹配,会带来冗余的计算量。所以结合更新的索引信息,可以对数据图进行增量匹配,并且索引能辅助加快匹配速度。 下面对增量匹配算法分成两种情况进行讨论:删除边和增加边(对于顶点的增删情况可以分解为边的删减)。 4.2.1删边的增量匹配算法 边的减少肯定不会导致匹配结果增加,同时如果减少的边不包含在原始匹配结果中也不会导致匹配结果的减少。只有当减少的边包含在原始匹配结果中,则需要将该边从匹配结果中删除。 算法4删边增量匹配算法 输入:原始匹配Gm,查询图GQ,删除边e,更新后的索引I。 输出:新的匹配Gnew。 1)IfGmcontainsethen 2) record the path setPinGmand the responding matched edge inGQ,the path inPcontainse; 3)Foreach pathpinPdo 4) computeδofpaccording toI; 5)Ifδ>1then 6) removepfromGm; 7)Else 8)Gnew=Gm; 9)If∃ a vertex or an edge inGQand no match inGm then 10)Gnew=∅; 11)Else 12)Gnew=the updatedGm; 13)ReturnGnew 步骤1根据删除的边,判断是否在原始匹配结果中,若不存在,则返回原结果。 步骤2若存在于原始匹配结果中,则记录结果中包含删除边的匹配路径以及所对应的GQ中被匹配的边。 步骤3对于受影响的匹配路径,根据更新的索引计算得δ值,若δ>1,从原匹配结果中移除。 步骤4得到更新后的匹配结果,若查询图中存在节点或边得不到匹配,则将匹配结果置为空。 步骤5返回更新后的匹配结果。 例3:图6和图7分别给出了数据图与查询图。可得到原始匹配结果:A1→B1→B2匹配(A,B),B2→D→C1匹配(B,C),B2→D匹配(B,D),E→C1匹配(E,C),E→D匹配(E,D)。 图6 数据图 图7 查询图 (1) 若删除边(B2,C2)不包含在原始匹配结果里,则返回原结果。 (2) 若删除边(A1,B1)对应(A,B)的匹配结果路径,计算得δ不满足,则移除该匹配。最后发现(A,B)不存在其他匹配,所以更新后的结果为空。 复杂度:算法的伪码在算法4中给出,复杂度为O(|P|),其中|P|是指原始匹配Gm中受影响的匹配路径的数量。 4.2.2增边的增量匹配算法 边的增加肯定不会导致匹配结果减少,同时如果增加的边影响力不够也不会导致匹配结果的增加。只有当增加的边使得受影响的AFF中节点对计算得的δ值由大于1变成小于等于1,则增加匹配结果。具体算法与上类似,与之相反的是判断值来增加结果而不是删除结果。 算法5增边增量匹配算法 输入:原始匹配Gm,查询图GQ,增加的边(vi,vj),AFF,更新后的索引I。 输出:新的匹配Gnew。 1)IfviorvjinGmthen 2)Foreach pair (vs,vt) inAFFdo 3)If∃(vqs,vqt) inGQandvqs,vshave the same label andvqt,vthave the same labelthen 4) computeδofpath(vs→vt); 5)Ifδ≤1then 6)Ifvsis new inGmthen 7) check if the edge patterns inGQwhich related tovqshave the matching paths; 8)Ifvtis new inGmthen 9) check if the edge patterns inGQwhich related tovqthave the matching paths; 10)Ifyesthen 11) add paths toGm; 12)Gnew=the updatedGm; 13)ReturnGnew. 步骤1如果增加的边的两个顶点都不包含在Gm中,则返回原结果;否则,执行步骤2。 步骤2对于AFF中的每对顶点(vs,vt),如果GQ中不存在需匹配的边与vs、vt具有相同的标签,则跳过;否则,执行步骤3。 步骤3根据索引计算path(vs→vt)的δ值,如果小于1,执行步骤4。 步骤4判断vs、vt哪个是新加入的顶点vnew,查询图中与vnew相关的边模式在数据图中是否存在与之匹配的路径。若不存在,跳过;否则,把得到的新匹配路径加到结果中。 步骤5返回更新后的匹配结果。 例4:如图6和图7所示,若增加(B2,C2)边,B2包含在原始结果中。查看AFF中的节点对,发现B2→C2符合匹配,并且查询图中与C相关联的边(E,C)能得到匹配路径E→C1→C2。所以,将B2→C2,E→C1→C2加入匹配结果。 复杂度:算法的伪码在算法5中给出,复杂度为O(|AFF|)。 任何更新操作都可以看成增边与删边操作的组合。增量匹配算法的执行时间可能会随着增加或删除边的数量的增加而增加,但是实际情况中,相较于大图而言,更新的操作量会远小于大图的规模。所以,相比于重新进行匹配查询,增量匹配会节省更多时间开销。若是更新的边数量超过原图的一半,则认为不是以更新为主而是进行了重构,就不采用本算法。 1) 数据集。采用了五个在snap.stanford.edu上得到的大规模真实图,这些图在图模式匹配和社交网络分析方面有着广泛的应用。这些数据集的详细情况见表5。 表5 数据集信息 2) 参数设置。在每个数据集中,SSG的个数设置为50,SSG的范围为70。此外,更新的顶点或边的数量范围为5到25,跨度为5;约束值变化范围为0.075到0.175,跨度为0.025。 3) 实现。实验实现了本文提出的SSG-IncMGPM和SSG-MGPM[19]这个解决图结构变化的MC-GPM问题最好的算法,以比较两个算法的效率。所有的算法都是使用Java实现的,在一台配备Intel Corei5、2.9 GHz CPU、8 GB RAM的PC机上运行。 图8-图17描述了在边删除、边插入的情况下,在五个数据集中不同更新规模的SSG返回MC-GPM查询答案时的平均查询处理时间。可以看出:(1) 随着删除或插入边数量的增加,两种方法的平均查询处理时间都增加;(2) 随着删除或插入边数量的增加,SSG-IncMGPM执行的时间的改进比率逐渐降低;(3) SSG-IncMGPM的查询处理时间总是小于SSG-MGPM的查询处理时间。 图8 删边时,Cit-HepTh数据集上算法执行时间 图9 删边时,Slashdot数据集上算法执行时间 图10 删边时,DBLP数据集上算法执行时间 图11 删边时,LiveJournal数据集上算法执行时间 图12 删边时,Twitter数据集上算法执行时间 图13 插入边时,Cit-HepTh数据集上算法执行时间 图14 插入边时,Slashdot数据集上算法执行时间 图15 插入边时,DBLP数据集上算法执行时间 图16 插入边时,LiveJournal数据集上算法执行时间 图17 插入边时,Twitter数据集上算法执行时间 实验结果表明:(1) 随着删除或插入边数量的增加,两种方法都需要花更多的时间来更新索引,因此两者都需要更多的查询处理时间;(2) 随着删除或插入边数量的增加,SSG-IncMGPM增量匹配时需要花时间处理更多受影响的边,并且更新索引比重也在增加,所以改进比率逐渐降低;(3) 无论插入或删除多少边,SSG-IncMGPM的性能总是优于SSG-MGPM,这是因为本文方法在面对SSG结构的变化时不需要再重新遍历整个图得到匹配结果。 图18-图27描述了删减边数量固定不变的情况下,在五个数据集上执行具有不同约束值的MC-GPM查询时的平均查询处理时间。可以看出:(1) 随着约束值的变化,两种方法的查询处理时间都相对稳定;(2) 在所有情况下,SSG-MGPM算法都比SSG-IncMGPM需要更多的处理时间;(3) SSG-IncMGPM算法执行时间改进比率保持较稳定状态。 图18 不同约束值,Cit-HepTh数据集上删边算法执行时间 图19 不同约束值,Slashdot数据集上删边算法执行时间 图20 不同约束值,DBLP数据集上删边算法执行时间 图21 不同约束值,LiveJournal数据集上删边算法执行时间 图22 不同约束值,Twitter数据集上删边算法执行时间 图23 不同约束值,Cit-HepTh数据集上增边算法执行时间 图24 不同约束值,Slashdot数据集上增边算法执行时间 图25 不同约束值,DBLP数据集上增边算法执行时间 图26 不同约束值,LiveJournal数据集上增边算法执行时间 图27 不同约束值,Twitter数据集上增边算法执行时间 实验结果表明:(1) 约束值的大小对算法的查询处理时间无较大影响,所以随着约束值的增大,两者的查询处理时间均保持稳定;(2) 由于不需要重新匹配得到结果,SSG-IncMGPM的性能一直优于SSG-MGPM;(3) 由于增删边数无变化,所以对SSG-IncMGPM和SSG-MGPM算法执行时间不会产生较大波动,两者均处于平稳状态。 综上,本文提出的SSG-IncMGPM考虑了强社交图,并增量维护了SSG索引的同时,对模式图进行增量匹配。实验结果表明,SSG-IncMGPM是解决具有挑战性的NP完全问题MC-GPM的有效方法。所提出的方法可以作为许多基于社交图的应用的核心,如在线社交网络中的信任/恶意网络查找和基于社交网络的众包中的可信作品选择。 本文提出了一个强社交图的概念,并给出了一个SSG的索引结构。在此基础上,提出了一种基于增量的SSG索引维护算法INC-SSG。最后,提出了一种基于INC-SSG的求解NP完全问题MC-GPM的SSG-IncMGPM算法。在五个真实的社交图上进行的实验表明,本文方法优于最新的方法。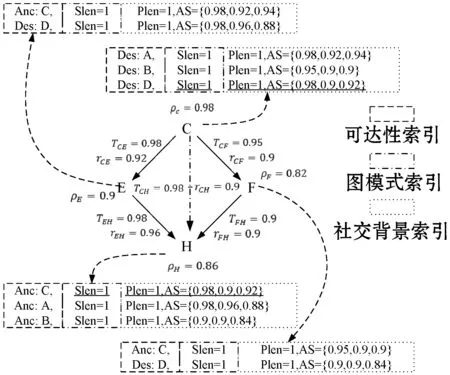
3.5 增删顶点的索引更新算法
4 增量匹配算法框架SSG-IncMGPM

4.1 路径匹配目标函数
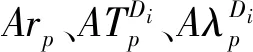
4.2 增量匹配算法

4.3 总 结
5 实 验
5.1 实验设置
5.2 实验结果和分析











6 结 语
