基于演化合成神经网络的光通信MIMO检测算法
2021-08-12陈晓宁
杨 恺 陈晓宁
1(东莞职业技术学院电子与电气工程学院 广东 东莞 523808)2(西北工业大学电子信息学院 陕西 西安 710072)
0 引 言
传统的时分复用、波分复用和偏振复用等技术成功提高了光通信系统的信道利用率和传输效率[1]。随着通信技术的发展,模分复用[2]技术进一步地提高了光通信的信道利用率,渐变型光信道的出现使得单个信道支持的模式数量日益升高,通过多输入多输出技术[3]能够有效地提升光通信系统的性能。多模传输虽然提高了光通信的效率和速度,但是在光传输过程中每个模式内和多个模式之间会发生非线性耦合的现象[4]。传统的光通信系统采用信道均衡化技术,在发送端发送训练信号,在接收端计算传输产生的误差,然后根据这些误差结果搜索均衡器的最佳参数集[5]。
许多专家学者对MIMO的均衡技术进行了深入研究,并且取得了卓越的成果。文献[6]提出基于自适应滤波算法的自适应均衡方法,该算法将信道均衡模型建模成滤波模型,滤波模型使MIMO系统均衡问题中均衡器的设计问题转化为自适应滤波中最优滤波器的设计问题。该算法具备较好的自适应学习能力,并且对非线性MIMO系统也具备一定的拟合能力。文献[7]将迫零均衡化(Zero Forcing, ZF)和最小均方误差 (Minimum Mean Square Error, MMSE)结合设计了自适应的MIMO均衡化算法,该算法对于不同形式的MIMO均表现出较好的性能,并且也实现了较好的非线性均衡效果。随着深度学习技术的发展,许多研究人员将深度学习技术应用于MIMO系统中,以期提高MIMO的学习效果。文献[8]将MIMO通信系统的发射端和接收端视为自编码器(Auto-Encoder)的编码和译码部分,利用交叉熵损失加权函数进行训练学习,从而解决MIMO的联合优化问题。虽然许多研究人员将深度学习技术成功运用于MIMO检测系统中,但是所支持的模式输入数量和输出数量较少,如文献[8]主要支持2个用户和4个用户的情况。
MIMO系统的规模越大,对应的深度神经网络规模随之扩大,而渐变型光信道现已支持较多的模式,需要建立大规模的神经网络才能较好地解决光通信MIMO检测问题。本文采用演化合成技术训练深度神经网络,将光通信系统MIMO的监督信息作为演化合成的先验信息,引导神经网络的演化,缩小神经网络的规模,提高网络的结构效率,避免在检测过程中花费过长的时间,有助于提高光通信的传输效率。最终采用40个模式的MDM光通信系统建立了实验,在模式耦合严重的情况下测试了本文MIMO检测算法的性能,本文算法的性能优于传统的ZF检测器和半正定松弛(Semi Definite Relaxation, SDR)等MIMO检测技术。
1 光通信系统的MIMO问题模型
1.1 发送端模型
图1所示为光通信系统的MIMO模型图。

图1 光通信系统的MIMO模型图
将N-模分复用的光通信系统表示为一个N×N的MIMO系统,MIMO的输入表示为d(t)=[d1(t),d2(t),…,dN(t)]T∈BN,其中:BN表示调制器产生的信号范围;N表示调制器数量。对应的MIMO输出设为d′(t)∈BN,其数学式为:
d′(t)=H-1Hd(t)
(1)
式中:H∈CN×N为信道矩阵,C表示复数集;H-1表示深度神经网络(DNN)的输出。图1中副载波复用模块包含N个正交相移键控(Quadrature Phase Shift Keying, QPSK)调制器,副载波频率设为fc。TXi模块包含一个马赫-曾德尔调制器(Mach-Zehnder Modulator, MZM)和一个光学载波。假设din为第i个信道的第n个输入比特。第i个QPSK调制器的输出为:
ai(t)=qiej2πfct
(2)
式中:qi=(di2n+jdi2n+1)表示一个QPSK符号。通过QPSK调制符号来控制光信号的强度(由马赫-曾德尔光调制器实现),所有光载波的波长相等。光调制器的输出为:
ri(t)=Pbias+PiRe[ai(t)]
(3)
式中:Pbias表示偏压所产生的光功率;Pi为光载波放大器;Re[ai(t)]表示ai(t)的实部。偏压控制通过调节MZM的工作点来维护电信号和调制光功率之间的线性关系,使用光纤耦合器将调制的光功率耦合成渐变型多模光纤的不同模式,光纤耦合器具备模分复用功能,其输出的所有光信号通过光纤传输,在传输过程中不同模式之间会发生耦合的现象。
1.2 接收端模型
接收端通过光纤耦合器将接收的光信号分为N个光束,光纤耦合器第i个输出端口的信号表示为:
(4)
式中:hij(t)表示信道矩阵H位置(i,j)的元素,hij(t)是一个复数。hij(t)的绝对值为耦合功率,hij(t)的相位表示副载波的时间偏差。因为在传输过程中发生模式耦合的现象,所以式(4)包含了TXi发送的信号和其他信号。第i个光探测器输出的电流为:
(5)
该电流产生一个电压信号gi(t),信号的计算式为:
(6)
式(3)的Pbias是一个直流值,接收端的带通滤波器将该直流信号过滤,所以式(6)中移除了该项。将该信号和副载波的频率fc相乘,最终输出的信号ki(t)变为:
(7)
采用低通滤波器处理第i个端口的信号,滤波后的信号变为:
(8)
式中:rxi(t)为N个传输信号的总和。N个端口的总输出为Rx(t)=[rx1(t),rx2(t),…,rxN(t)]T∈CN。
1.3 深度神经网络
图2所示是本文DNN的结构。

图2 深度神经网络的结构
DNN的输入向量为:
x0=[Re(rx1(t)),lm(rx1(t)),Re(rx2(t)),
lm(rx2(t)),…,Re(rxN(t)),lm(rxN(t))]
(9)
式中:x0的长度为D=2N,假设R表示实部集,将一个M层的前馈神经网络表示为一个映射函数f(x0;θ):RD0→RDM,该函数经过M次迭代最终将输入向量x0∈RD0变换为输出向量xM∈RDM,迭代过程定义为:
xm=fm(xm-1;θm)
式中:fm(xm-1;θm):RDm-1→RDm为第m层的映射函数;θm为神经网络的参数;xm-1为前一层的输出向量。将神经网络的参数集表示为θ={θ1,θ2,…,θM}。首先训练完全连接的神经网络模型,网络的第m层表示为:
fm(xm-1;θm)=σ(Wmxm-1+bm)
式中:Wm∈RDm-1×Dm;bm∈RDm;σ()为激活函数。激活函数对输入向量的每个元素进行处理,记为[σ(u)]i=σ(ui),第m层的参数集表示为θm={Wm,bm}。
2 神经网络训练
2.1 深度全连接神经网络的训练方法
将DNN的训练集表示为(x(i),y(i)),i=1,2,…,S,其中y(i)为输入x(i)的期望输出,S为训练样本的总数量。将训练集经过光通信系统传输,接收不同信道条件下的Rx,设CN表示给定信道的相关属性,通过CN可观察出还原该信道MIMO信号的难度。信道矩阵H的CN矩阵表示为20log10(‖H‖‖H-1‖)≥0(dB),其中‖·‖表示求范数的运算。CN越接近0(dB),说明MIMO信道的质量越高。矩阵H反映了光纤耦合器和多模光纤的特性,光纤的特性包括模式色散、模式相关效应和模式耦合串扰等因素。首先采用不同CN数据对神经网络进行训练,训练的目标函数定义为:
(10)
式中:L(·,·)为每个样本的成本函数;x(i)为神经网络的输入;f(x(i);θ)为神经网络的输出。采用MSE作为成本评价函数,将式(10)改写为:
(11)
采用一阶优化算法Adam[9]基于成本函数的梯度完成训练过程,Adam[9]是一种自适应调节学习率的算法,能够动态地更新参数θ。Adam采用梯度一阶矩和二阶矩的估计来计算每个参数的自适应学习率。成本函数J(θ)含有噪声,其目标是最小化J(θ)的期望值。首先,随机初始化参数θ=θ0,一阶矩、二阶矩分别初始化为s=0和β=0。一阶矩和二阶矩的指数衰减率ρ1和ρ2分别初始化为缺省值0.9和0.999,步长设为缺省值ε=0.001。从训练集采样的mini-batch表示为{x(1),x(2),…,x(ζ)},对应的期望输出为{y(1),y(2), …,y(ζ)}。成本函数的梯度计算式为:
(12)
式中:ξ表示输出数量;f()为映射函数;i为输入序号。一阶矩估计的更新方法为:
snew=ρ1s+(1-ρ1)g
(13)
二阶矩估计的更新方法为:
βnew=ρ2β+(1-ρ2)g⊙g
(14)
式中:⊙为矩阵的点积运算。
一阶矩的实际偏差为:
(15)

二阶矩的实际偏差为:
(16)

(17)
更新的参数θ为:
θnew=θ+Δθ
(18)
重复计算式(12)-式(18),最终参数θ达到收敛,此时获得的DNN全连接网络可以用来检测MIMO信号。但对于大规模的MIMO,神经网络的规模也较大,导致检测的时间较长,影响光通信系统的传输效率。
2.2 神经网络结构的化简
采用两个二值随机变量表示网络的神经元和权重,对深度神经网络的结构进行编码,变量取值1和0表示该神经元或者权重是否存在于网络中。第2.1小节训练的完全连接神经网络表示为S,S={sl,i,i=1,2,…,Il,l=1,2,…,L}是一个二值变量集,其中:sl,i表明第l层、第i个神经元是否存在;L表示神经网络的最大层数;Il表示第l层的神经元最大数量。
演化合成的目标[10]是通过迭代的方式分析神经网络结构关于时间的最优概率分布,再通过一个演化的形式逐渐合成缩小的深度神经网络。每次迭代基于父代的神经网络随机合成子代网络,随机合成的概率P(Sg)定义为:
P(Sg)=P(Sg|Wg-1)·F
(19)
式中:P(Sg|Wg-1)为合成的概率模型;F表示外部环境因素。每次迭代训练子代网络,以模型准确率为目标,以效率和网络结构的多样性为约束条件。环境因子F作为演化过程的先验约束条件,用以缩小网络结构的搜索空间,寻找其中最佳的概率分布来建模最优的网络结构,合成概率模型P(Sg)作为神经网络的遗传编码。

为了支持多层神经网络,将P(Sg|Wg-1)分解为多变量概率分布,最终合成子代深度神经网络,分解方法为:
P(Sg|Wg-1)=
(20)

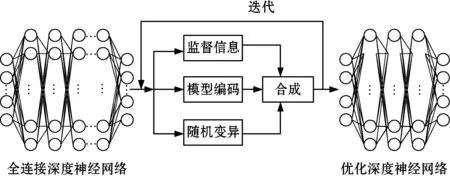
图3 基于演化合成的深度神经网络优化算法
3 实 验
3.1 实验建立
在实验室搭建了仿真实验的MDM光通信系统,图4是实验室的光通信系统模型。神经网络的编程环境为Intel(R) Core(TM) i7-4790 CPU, 3.6 GHz,内存为16 GB。
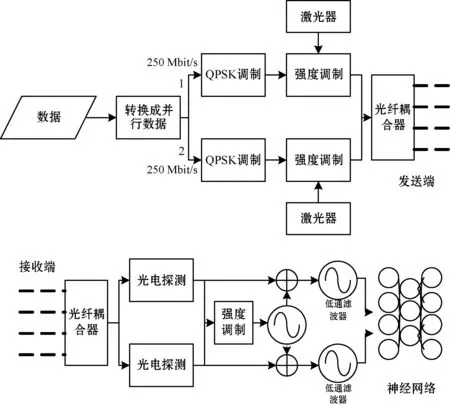
图4 实验室的光通信模型
利用MATLAB软件生成随机数据,通过软件将数据转化为并行数据形式,将数据分为信道1和信道2。使用QPSK将信道调制为125(Mbaud/s),两个信道的副载波频率为250 MHz。使用Mach-Zehnder调制器进行光学调制[12],采用两个1.55 μm的前馈激光器(DFB-LD)产生激光信号。发送端将两个光信号耦合,产生不均匀的激光模式,光纤是50 μm芯径双包层的光纤。
接收端的光纤耦合器将信号分为两束,光探测器以2 Gbit/s的速度检测光信号,然后经过模数转换器获得数字信号,解调后的信号包含两个信道信号。
3.2 实验数据采集
采集两个数据集,分别为训练集和测试集。同步采集通信系统发送端数据集和接收端数据集,采集的数据集组织成元组形式(x,y),x为输入数据,y为x对应的期望输出数据。
3.3 完全连接神经网络训练实验
首先需确定隐藏层数量和神经元数量,通过一组实验观察不同超参数的检测性能。共设立11个信道条件,信道的信噪比分别为3、5、7、8、10、12、14、16、18、19、19.5 dB,使用ZF技术来计算信道矩阵。接收端将11个信道条件的数据保存为11个数据集,每个信道收集了2 000 000个符号,选择每个信道的200 000个符号作为训练集。实验设备是2×2的MDM光通信系统,共有4个输入符号和4个输出符号。如果QPSK调制器1输出的符号为(+1-j1),QPSK调制器2输出的符号为(-1+j1),那么期望的接收符号为(+1-1+1-1),该期望值也是DNN的期望输出值。
采用误码率(Bit Error Rate, BER)[13]评估神经网络实际输出值和期望输出值的误差,不同超参数对应的实验结果如图5所示。因为多模光纤具有高度非线性的特点,所以单元数量越多,误码率越低,单元数量达到20,误码率达到收敛。隐藏层的数量越高,误码率越低,而7层隐藏层的性能低于6层隐藏层,所以本文的完全连接神经网络超参数设为6层隐藏层,每个隐藏层为20个神经元。

图5 完全连接神经网络的超参数实验
图6是6个隐层(20个单元)的收敛曲线,其中mini batch设为50。神经网络的收敛点为epoch=12,将收敛的模型用于MIMO检测实验。

图6 神经网络的收敛曲线
DNN前向传播和后向传播的计算复杂度分别为O(n2m+m3(l-2))和O(I(n3m+m4(l-2))),其中:n为输入向量的长度;m为隐层的单元数量;l是DNN的总层数;I为梯度下降的迭代次数。将收敛网络放入MDM光通信系统进行MIMO的检测实验。
3.4 神经网络的演化合成实验
对上文获得的完全连接神经网络进行演化合成处理,合成的化简神经网络结构为“4-7-12-5-18-7-7-4”。然后统计两个神经网络对测试集的平均符号检测速度,完全连接神经网络大约每秒检测24.5个符号,而合成神经网络大约每秒检测134.3个符号,有效地提高了神经网络的检测效率,见表1。提高MIMO的检测效率对光通信系统的传输速度也是一个极大的提升。

表1 演化合成神经网络的结构
3.5 MIMO检测实验的结果
上文训练的完全连接DNN模型简称为FDNN(Full-connected Deep Neural Networks),演化合成DNN模型简称为RDNN(Reduced Deep Neural Networks),将两个网络分别集成到MDM光通信系统中进行MIMO检测的实验。此外选择经典的迫零检测器(ZF)[14]和半正定松弛检测器(SDR)[15]作为对比方法,SDR检测器的迭代次数设为10。4个MIMO检测算法采用相同的输入数据集和期望接收数据集,图7是4个检测算法在不同信道条件下的误码率变化情况。在不同的信道条件下,ZF的误码率均最高,SDR的误码率明显低于ZF,本文的两个神经网络检测器则明显优于SDR。比较FDNN和RDNN两个检测器的误码率,虽然RDNN的检测性能有所衰减,但是其检测效率明显高于FDNN,而端到端传输时延是通信系统的关键指标。

图7 4个检测算法在不同信道条件下的误码率值
质量参数Q-factor是另一个评价MIMO检测性能的指标,Q-factor的计算式为:
(21)
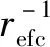
表2为不同信道条件下FDNN和RDNN的Q-factor数值结果。结果显示,当信噪比为19时,FDNN和RDNN的Q-factor分别为9.78 dB和10.11 dB,根据光通信系统的相关文献[16-17],该指标值也是较为理想的结果。

表2 神经网络的Q-factor结果 dB
实验结果表明了本文所设计FDNN的有效性,FDNN提高了光通信MIMO检测的准确率。在本文的实验条件下,训练完全连接神经网络的时间大约为4 min。
4 结 语
本文采用演化合成技术训练深度神经网络,将光通信系统MIMO的监督信息作为演化合成的先验信息,引导神经网络的演化,缩小神经网络的规模,提高网络的结构效率,避免在检测过程中花费过长的时间,有助于提高光通信的传输效率。最终采用40个模式的MDM光通信系统建立了实验,在模式耦合严重的情况下测试了本文MIMO检测算法的性能,本文算法的性能优于传统的ZF检测器和半正定松弛等MIMO检测技术。本文设计了演化合成技术提高深度神经网络的结构效率,并通过实验验证了化简神经网络的有效性,化简神经网络牺牲了可忽略的检测准确率,但是检测速度得到了极大的提升,在通信系统中,端到端传输时延是一个极为重要的考量指标。
