隧道内地铁列车车内噪声预测分析

冯青松，周 豪，陈艳明，张 凌，罗信伟

(1.华东交通大学 铁路环境振动与噪声教育部工程研究中心，南昌 330013；2.广州地铁设计研究院股份有限公司，广州 510000)

随着城市轨道交通的迅速发展，地铁系统以其快捷、高准点率、载客量大、污染轻、安全性好等诸多优势，逐渐成为各大中城市公共交通的骨干。伴随着我国轨道交通的发展，列车振动噪声问题也成为亟待解决的问题之一，车内振动噪声直接影响司机和乘客的乘坐舒适性，并成为衡量地铁质量的一个重要指标[1]。目前，国内外学者对列车车内噪声问题进行了一系列研究工作。在高速列车运行引起车内振动与噪声的研究中，袁旻忞等[2]利用工况传递路径分析(OPTA)得到了高速列车车厢中心处的主要噪声源贡献量；罗文俊等[3-4]采用混合FE-SEA法分析了车体的车内结构噪声特性；刘加利等[5]基于SEA理论计算了脉动压力激励下车内高频气动噪声，并提出了有针对性的降噪优化方案；柳明等[6]研究了我国某型高速列车在明线和隧道运行时的车内振动噪声特性及其随速度的变化规律；孙强等[7]通过测试研究了运行环境温度对车内噪声的影响。Dai等[8]提出一种改进的统计振动与声能量流的方法来预测车内噪声，并结合试验验证了该方法的准确性和有效性。Zhang等[9]通过试验分析了高速列车的车内外声源分布情况。而在地下列车运行引起车内振动与噪声的研究中，耿烽等[10]利用声传递向量技术对地铁A型铝合金车辆进行了噪声源分析和噪声响度评价；刘国漪等[11]分析了地铁列车车内低频噪声特性及车身板件声压贡献量；薛红艳等[12]通过试验的方法分析了不同速度下车内不同位置噪声分布规律。Li等[13]研究了钢轨扣件刚度对地铁列车车内噪声的影响；Han等[14-15]研究发现波磨地段车内的声压级更大，打磨钢轨能够有效降低车内噪声。Zhao等[16]通过安装钢轨减振器对地铁车内噪声进行试验研究，发现钢轨减振器可以降低车内噪声8 dB。

上述学者的研究为车内噪声的预测分析提供了理论依据。但目前对车内噪声特性研究多以高速列车为主，针对隧道内地铁车厢内部噪声研究较少，且现有研究仅考虑了轮轨力作用下车内噪声，忽略了轮轨噪声的影响，结构声和空气声对车内噪声的作用机理研究有待完善。为此，本文以广州轨道交通7号线列车噪声试验为依据，建立了隧道-车体有限元-边界元声学分析模型。基于地铁B型车车轨耦合模型和现场试验获取车体振动激励和轮轨噪声激励，研究了结构声和空气声对车内噪声的影响规律。本文研究成果可为改善地铁车内声学环境提供参考。

1 数值分析模型

1.1 模型概况

本文以地铁B型车为研究对象，列车车体为铝合金中空型材结构，由底架、侧墙、端墙、顶板、地板等组成，在VA One中，建立车身结构有限元模型和车内声腔有限元模型。隧道断面采用广州地铁某线圆形隧道实际尺寸进行建模。将整车有限元模型与声腔有限元模型耦合，采用边界元流体将其与隧道连接，得到隧道-车体有限元-边界元模型如图1所示。

图1 隧道-车体有限元-边界元模型(隐去部分门窗)

1.2 计算参数

查阅相关工程材料手册列出部分结构材料属性如表1。

表1 部分结构材料属性

1.3 列车荷载激励提取

1.3.1 振动激励

列车轮轨作用力经转向架悬挂系统衰减后形成二系悬挂力，作用于车体底部引发车体相关部件振动，从而辐射结构噪声。二系悬挂力可通过多体动力学软件UM获取。本文按照表2中的建模参数，建立地铁B型车车轨耦合动力学模型，整车由1个车体、2个构架、4个轮对和8个轴箱组成。通过定义轮轨接触几何关系、子系统的铰接及力元等参数的设定，将车体及轨道各部分相互连接、耦合。分别提取垂向、横向、纵向二系悬挂力作为列车的振动激励。车体动力学模型如图2所示。

表2 地铁B型车计算参数

图2 列车多刚体动力学模型

列车运行速度设为60 km/h，线路曲线半径为400 m，采用GJY-T-EBJ-2型轨检小车获取轨道实测不平顺谱，轨底坡为1/40。在轮轨不平顺的激励、各刚性体和减振系统的相互作用下，得到列车的二系悬挂力时域数据，经傅里叶变换转化为可输入声学软件VA One的载荷。列车垂向二系悬挂力时域图及频谱图(以前转向架为例)如图3、4所示。

图3 二系悬挂力时域信号

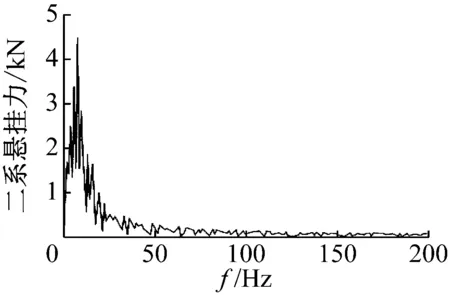
图4 二系悬挂力频谱

1.3.2 轮轨噪声激励

列车车轮和钢轨之间相互作用产生振动向外辐射噪声，主要通过空气传播和结构传播两种途径传递至车内[17-18]，是地铁列车车内噪声的主要声源之一。本文通过现场试验获取轮轨噪声激励。为保证车内噪声数据准确性，试验在当天地铁停运后进行，列车为地铁B型车，平均运行速度60 km/h，单线行车。采用丹麦GRAS声传感器和德国Head公司DATaRec 4 DIC24数据采集仪进行轮轨噪声数据采集，并用ArtemiS软件对多组数据进行统计分析。图5、图6分别为列车转向架区域的噪声时域和频谱图。

图5 实测轮轨噪声时域图

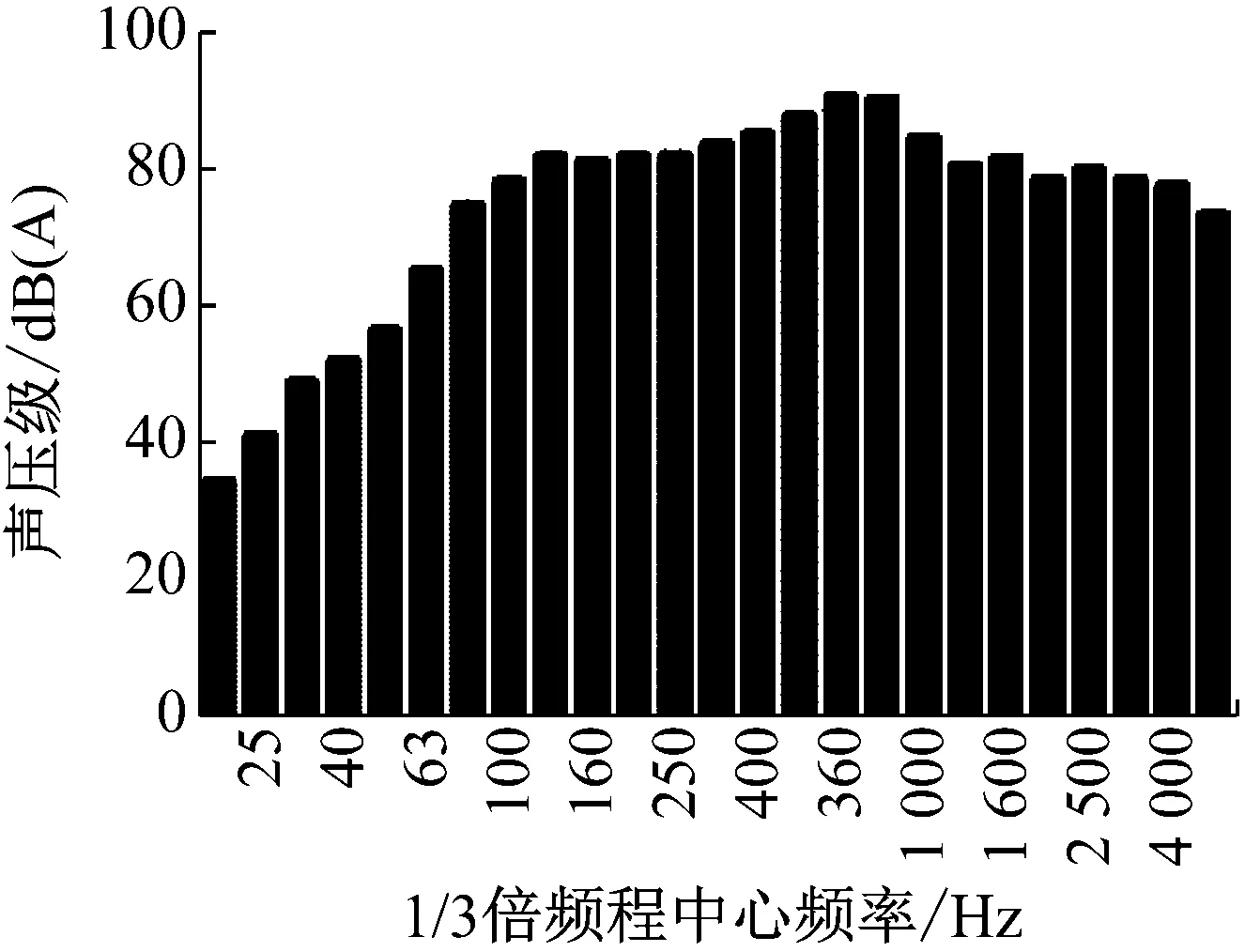
图6 实测轮轨噪声1/3倍频程图

2 试验与列车声学模型验证

2.1 试验概况

为验证车体声学模型的准确性，选择广州地铁7号线进行试验。广州地铁7号线一期线路全长17.41 km，全部为地下线，列车采用6节编组B型列车。依据GB/T 3499—2011《声学轨道车辆内部噪声测量》[19]和GB/T 14892—2006《城市轨道交通列车噪声限值和测量方法》[20]，分别在前转向架上方、客室中间、后转向架上方布置噪声测试传感器，通过美国NI数据采集仪和Gras传声器对每个测点数据进行采集。测试采用行车期间数据不间断采集，采样频率为25 000 Hz。若相同测量条件下该组读数之最大差值超过3 dB，则重新进行测量。取20组测量数据的算术平均值作为实验结果。图7为车体纵向剖面图及相应的测点布置情况，噪声测点均在地板上方1.2 m(坐姿位置)处，测点编号从左至又依次为P1、P2、P3。图8为现场实测照片。

图7 噪声测点布置

图8 现场测试图

2.2 列车声学模型验证

将二系悬挂力、轮轨噪声作为车体声学模型输入激励并计算列车内噪声，如图9所示为地铁列车声学模型外部激励加载示意图，二系悬挂力激励施加在车体与二系悬挂(共四个)的连接处，轮轨声激励施加在车体模型底部。在VA One中，设置与车内噪声测试试验相同位置的车内声学传感器，如图10所示，声学传感器均设在地板上方1.2 m(坐姿位置)处，分别以A1、A2、A3表示。

图9 声学模型载荷激励

图10 车内声学传感器设置

计算得到车内A1、A2、A3点处的声压级。采用各测点20组列车不同时段相同运行工况的1/3倍频程分析多组数据在不同频段的统计规律，进而得到3个测点的各频段噪声统计特性，基于这20组数据做出1/3倍频程频谱均值曲线。将仿真值与20组试验值(图11中表示为虚线)以及均值进行对比，如图11所示。

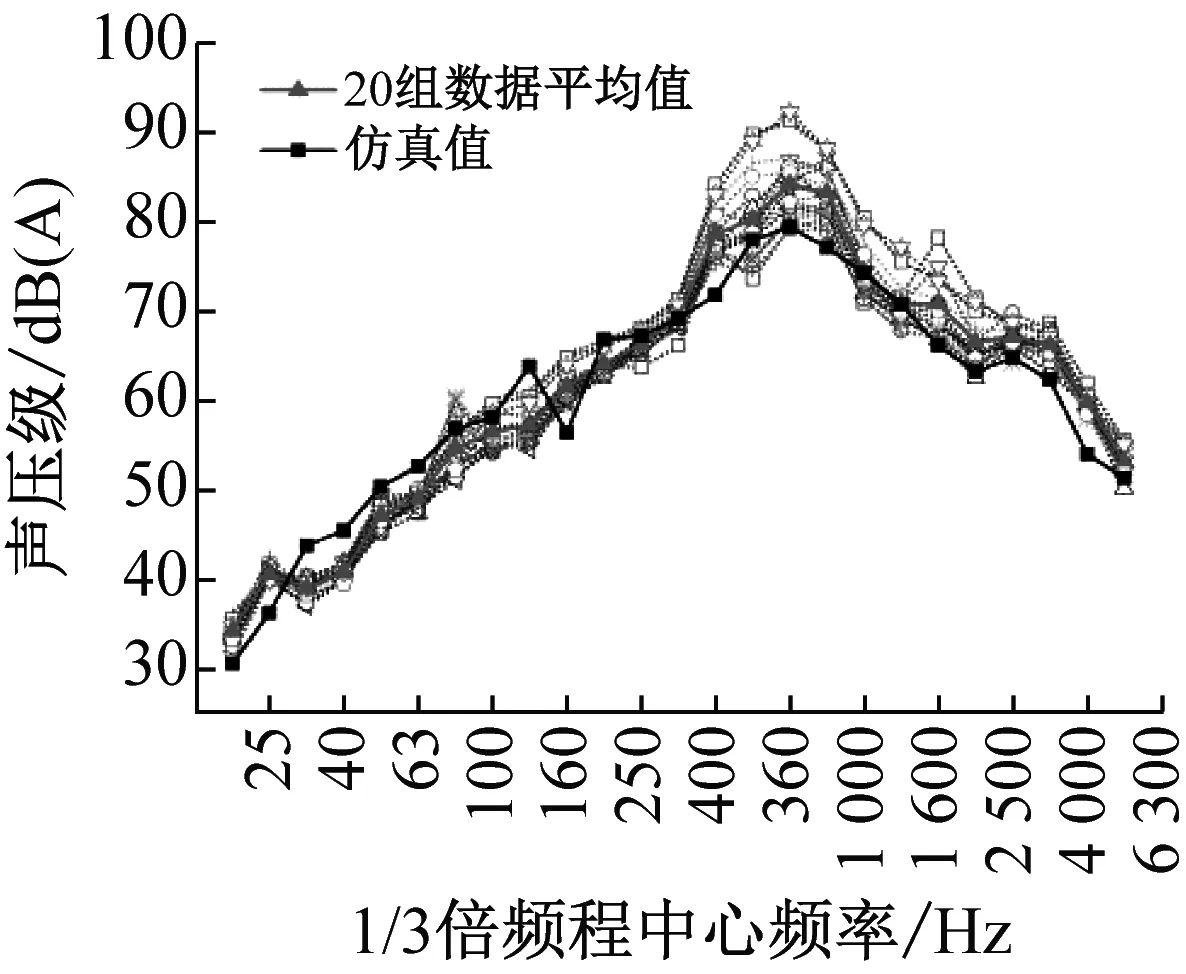
(a)A1点

从图11可以看出，总体上车内噪声仿真与试验声压级值基本一致，主要频段出现在200～1 600 Hz。在分析频段200 Hz以下，仿真曲线在试验曲线上下方波动，这主要与仿真时车体板块结构的简化有关，且实际中列车车体存在缝隙，在数值模型中较难实现，以及未考虑列车车内设备噪声的影响，导致误差进一步增大，使仿真结果出现波动，但是在200 Hz以上频段，数值计算与试验的误差基本上小于3 dB，符合工程精度的要求，且车内各测点的仿真与试验声压级总值误差均小于3 dB。综上所述，该声学模型能够较为准确地对地铁列车车内噪声进行预测。

3 车内结构声与空气声影响特性分析

地铁列车车内结构声主要来自转向架及附属设备的振动激发车体部件振动，向车内辐射产生的噪声；空气声则透过车体壁板、门窗，以及通过门缝等缝隙传播至车内，本文建立的车辆模型是密闭无缝的，轮轨声激励作用于车体底部时主要通过板件透射的方式向车内传递空气声。

3.1 工况设置

为了研究结构声和空气声对车内噪声的影响，设置了以下四种工况：

工况1：结构声荷载单独作用车体时车内噪声，即在车体底部施加振动激励；

工况2：空气声荷载单独作用车体时车内噪声，即在车体底部施加轮轨声激励；

工况3：结构声和空气声荷载同时作用车体时车内噪声，即在车体底部施加振动激励和轮轨声激励；

工况4：20组实测车内噪声数据平均值。

3.2 数值计算结果分析

根据文献[19-20]选取车体内3点为观察点，如图10中观察点A1～A3。表3给出了不同工况下的车内各观察点的总声压级。图12为不同工况下各观察点的三分之一倍频程曲线。

表3 车内各观察点总声压级

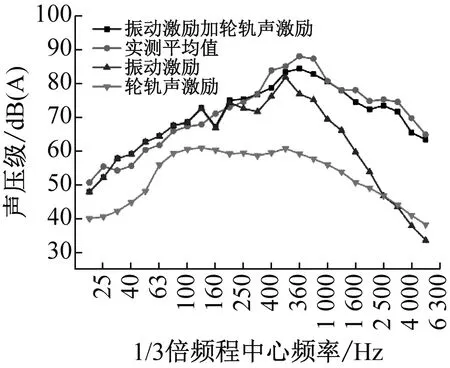
(a)A1点

由表3可知：

(1)仅在振动激励作用下，车内各标准点结构噪声总声压级相差较小，最大差值低于1 dB(A)，转向架上方结构噪声比车体中心结构噪声高约0.5 dB(A)，主要是因为振动激励主要是由转向架传向车体，振动激励越大，车内噪声越大。因此可考虑对车底转向架处受载部位进行减振以降低转向架上方噪声。

(2)在振动激励和轮轨声激励2种荷载共同作用下，车内噪声声压级明显大于振动激励单独作用下的车内结构噪声，差值约为4 dB(A)。考虑2种激励共同作用和只考虑振动激励时，计算得到的车内声压级与实测结果最大误差分别为2.17 dB(A)和6.08 dB(A)，前者可降低误差约4.61%。说明轮轨声激励对车内噪声的贡献量并不可忽略，在列车车内噪声预测中作为声激励应被充分重视。

(3)车速60 km/h下，结构声荷载下车内中心处声压级为78.2 dB(A)，比空气声荷载作用下车内中心处声压级高约21 dB(A)。说明地铁列车在低速运行状态下，结构声是车内总声压的主要成分。

从图12可以得出：

(1)在不同荷载激励工况下，车内各标准点的1/3倍频程声压级图变化趋势基本一致，均呈宽频带分布，噪声A声级呈现先上升后下降的趋势，能量主要集中在200～1 600 Hz频段，转向架和车体中心上方1.2 m处噪声的A声级都在630 Hz左右出现明显峰值，对应峰值分别为84.08 dB(A)、81.73 dB(A)、82.76 dB(A)。

(2)在20～200 Hz频段内，列车在振动激励下的A声级和2种激励共同作用下的A声级基本重合，最大差值为0.95 dB(A)，这是因为轮轨噪声的能量主要集中在200 Hz以上(如图5)，说明轮轨声激励对车内低频噪声作用并不明显。因此，降低车内低频噪声可优先选择控制车体结构振动，如降低轮轨冲击力、车体敷设阻尼材料等。

(3)仅在轮轨声激励下，车内噪声呈宽频分布，无明显峰值；仅在振动激励下，车内噪声A声级随着频率升高呈现先增大再减小趋势，在500 Hz达到最大值为75.9 dB(A)，噪声能量主要集中在200～800 Hz；500～5 000 Hz频段内，车内A声级大幅衰减，和2种激励共同作用下车内A声级差值逐渐增大，说明此时车内噪声主要由空气声主导。因此，在进行车内高频噪声控制时，可以考虑对轮轨噪声进行优化，如采用阻尼钢轨等措施。

(4)在列车车内噪声研究中，对比单一振动激励，同时考虑轮轨声激励时，车内噪声A声级更接近实测结果，在列车车内噪声预测和车内噪声声源控制中应得到充分重视。

4 结 论

本文建立了隧道-车体有限元-边界元声学分析模型，分析了地铁列车车内噪声特性，通过地铁车内噪声试验对分析模型进行验证，并研究了结构声和空气声对车内噪声的影响规律。总结如下：

(1)本文所建立模型考虑了振动激励和轮轨噪声激励，计算结果与实测结果吻合较好，该模型能够快速准确地预测地铁列车车内噪声。

(2)车内各标准点噪声A声级呈现先上升后下降的趋势，在630 Hz存在明显峰值，能量主要集中在200～1 600 Hz频段内。车体转向架上方A声级比中心上方大1.02～2.35 dB(A)，因此可考虑对车底转向架处受载部位进行减振以降低转向架上方噪声。

(3)仅在振动激励作用下，车内各标准点结构噪声总声压级相差较小；振动激励和轮轨声激励共同作用下车内A声级更接近实测结果，轮轨噪声在列车车内噪声预测和车内噪声声源控制中应得到充分重视。

(4)结构声对车内噪声的主要影响频段在20～200 Hz，空气声对车内噪声的主要影响频段在200～5 000 Hz，其中500～5 000 Hz频段最为显著。因此在降低车内低频噪声时可优先选择控制车体结构振动(如降低轮轨冲击力、车体敷设阻尼材料等)；在进行车内高频噪声控制时，可以考虑对轮轨噪声进行优化(如采取阻尼钢轨等措施)。