水下悬浮隧道张力腿的时滞减振控制研究

童俊辉，彭 剑,2，符 翔，孙洪鑫,2

(1.湖南科技大学 土木工程学院，湖南 湘潭 411201；2.湖南科技大学 结构抗风与振动控制湖南省重点实验室，湖南 湘潭 411201)

悬浮隧道(submerged floating tunnel,SFT)，又称Archimeders桥[1],是一种跨越长水道和深海峡潜在的交通结构物，主要依靠自身结构的浮力和支持系统保证其在固定位置，较传统隧道和桥梁有其特有的优势，具有广泛应用前景。但由于海洋环境复杂，悬浮隧道的振动和稳定性问题亟需解决。近年来，水下悬浮隧道及悬浮隧道张力腿引起学者大量关注。为了解决悬浮隧道在水流作用下的动力响应问题，项贻强等[2]对管体和锚索系统的参数振动和涡激振动进行了研究，结果表明，管体的初始扰动对锚索瞬态振幅有很大影响；易壮鹏等[3]对张力腿悬浮隧道的动力学模型和自振特性进行了研究；闫宏生等[4]研究了海流作用下悬浮隧道缆索的运动响应；孙胜男等[5-6]对锚索-隧道耦合非线性参数振动进行了研究，并对不同参数激励下隧道张力腿的振动进行了分析；李焱等[7]研究了畸形波作用下张力腿平台的动力响应，考虑张力腿平台的六自由度运动与张力腿非线性恢复刚度，建立非线性耦合运动方程；常爽等[8]通过波浪聚焦和波列叠加模型模拟生成了畸形波，结果表明畸形波和二阶波浪力会引起张力腿平台纵荡和垂荡的大幅运动；刘宇等[9]研究了锚索倾角对不同截面悬浮隧道运动响应影响；黄磊等[10]总结并分析了近些年水中悬浮隧道的研究进展。

此外，为了抑制张力腿的大幅振动，振动控制研究显得尤为重要。主动控制在土木工程结构的抗风、抗振和自适应修复等问题上有了大量的研究和应用，提高了结构稳定及性能[11]。但在主动控制系统中，时滞问题是不可避免的，其中包括本身自有的时滞以及外部引入的时滞。胡海岩等[12]从时滞动力学系统的特点、研究方法、动力学等问题出发，对时滞动力学研究进展作了综述；Masoud等[13-15]研究了结构振动的时滞输出反馈控制器设计，并利用时滞状态反馈控制起重机的振动问题，有很好的控制效果；陈龙祥等[16]研究了时滞对系统稳定性的影响，指出主动控制系统的时滞存在可利用的价值；Peng等[17]对压电弹性梁非线性共振响应的时滞反馈振动控制进行了研究;Sandip等[18]对时滞非线性反馈振荡器的参数激励和Hopf分岔进行了分析。

水下悬浮隧道是一种未来的新型交通结构，目前悬浮隧道的预想设计有浮筒式、墩柱式以及锚索(张力腿)式，其中张力腿式根据张力腿的倾斜角度不同，分为垂直式、倾斜式和混合式等。本文采用时滞减振技术对垂直式张力腿悬浮隧道进行振动控制研究，将隧道管体假设成质量点，根据Euler-Bernoulli梁理论和时滞反馈控制策略，考虑高阶非线性影响，建立了张力腿的参激振动模型，将隧道管体的竖向和横向运动简化成简谐运动，并着重分析张力腿的运动特性及时滞减振效果。通过实际算例，调整不同的控制增益和时滞量，验证了时滞反馈控制对张力腿振动的抑制效果，为未来水下悬浮隧道的实际应用及稳定控制提供参考意见。

1 数学模型

图1是基于张力腿竖直锚定的水下悬浮隧道示意图及其力学简图，考虑轴向和横向耦合，将张力腿简化成一根下端固定铰支，上端可移动铰支的非线性梁模型。

(a)水下悬浮隧道示意图

由于大长径比，忽略转动惯量和弯曲刚度的影响,并考虑材料的阻尼，根据Hamilton变分原理，得到张力腿振动控制方程[19]：

(1)

fy+Fcδ(x-xd)

(2)

式中：“·”为对时间t求导，“′”为对坐标x求导;ρ为材料的密度;A为横截面面积;c为线性阻尼系数;E为材料弹性模量;I为张力腿横截面的惯性矩;u和v分别为轴向和横向的位移;Fc为控制力;δ是Dirac delta函数;xd表示控制点的位置。

边界条件为：

(3)

式中：Ua(t)、Va(t)分别为隧道管体竖向和横向运动形式，为便于理论分析，本文将张力型悬浮隧道管体的竖向和横向振动简化为简谐振动，并将竖向和横向谐振的位移记为[20]：

(4)

式中：fx和fy分别为轴向和横向单位长度的分布力，fx为单位长度的浮力与重力的差值：

fx=ρfAg-ρAg

(5)

fy为张力腿横向运动所引起的流体阻尼力，根据Morison方程进行计算[21]:

(6)

式中：ρf为海水密度;A为张力腿的横截面积;g为重力加速度;D为张力腿直径;Ca、Cd分别为附加质量系数和黏性力系数;UL0、VL0分别为隧道管体垂荡和纵荡的幅值;ωa为其振动的圆频率。

因为张力腿长径比较大，忽略方程(1)～(2)中转动惯量的影响，考虑上端隧道管体的横向和竖向振动，以及预张力所引起的变形，运用Galerkin法，将轴向位移和横向位移的时间变量和空间变量分离，将其表示为振动函数和振型函数的乘积叠加，即：

(7)

(8)

(9)

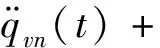
(10)

由于张力腿的横向波速远小于其纵向波速，故假设张力腿以拟静态方式进行轴向变形[22],忽略方程式(9)中的惯性力、外激励则有：

(11)

将方程式(11)代入方程式(10)，有：

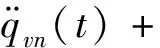
(12)

本文采用速度时滞反馈策略，记为如下形式：

(13)

(14)

其中：

μn=2ωnξ，

2 线性稳定性分析

本节研究了系统线性稳定性,并得到了系统稳定性图，以此为依据，得到系统的稳定域，为第3节的实例分析中参数的选取提供指导意义。

将方程(14)线性化，并令f=0，可得：

(15)

式中：ωn为张力腿固有频率，方程(15)的解形式如下：

qvn=Ane(ξn+iλn)t

(16)

式中：An是振幅;ξn是阻尼系数;λn为响应频率，将方程(16)代入方程(15)，分离实虚部，并令其分别等于零，得到：

sin(2πλnγ)+2ξnλncos(2πλnγ)]=0

(17)

cos(2πξnγ)-2ξnλnsin(2πξnγ)]=0

(18)

式中：γ=τ/2π，通过分析发现，系统的线性稳定性由阻尼系数ξn决定，当ξn>0时，系统是稳定的，而当ξn<0时，系统不稳定，因此为了得到线性稳定性边界条件，令ξn=0，求解方程(17)～(18)，得到：

通过方程(19)～(20)，得到稳定性区域(见图2)。如图2所示，在(τ,k1)平面内，随着τ的增大，稳定性范围逐渐减小；当确定时滞τ为某一值时，系统的稳定随着k1的变化而发生改变，即由稳定变为不稳定或者由不稳定变为稳定。因此，可以通过调节时滞和增益来改变系统的稳定性。

图2 系统稳定性图(n=1，μ1=0.008 8)

3 数值分析与讨论

本节以某拟建悬浮隧道参数进行算例分析，结构基本参数见表1[23]。其中，增益值和时滞量根据图2系统的稳定性图，选取了稳定域中的几个参数，进行比较分析。

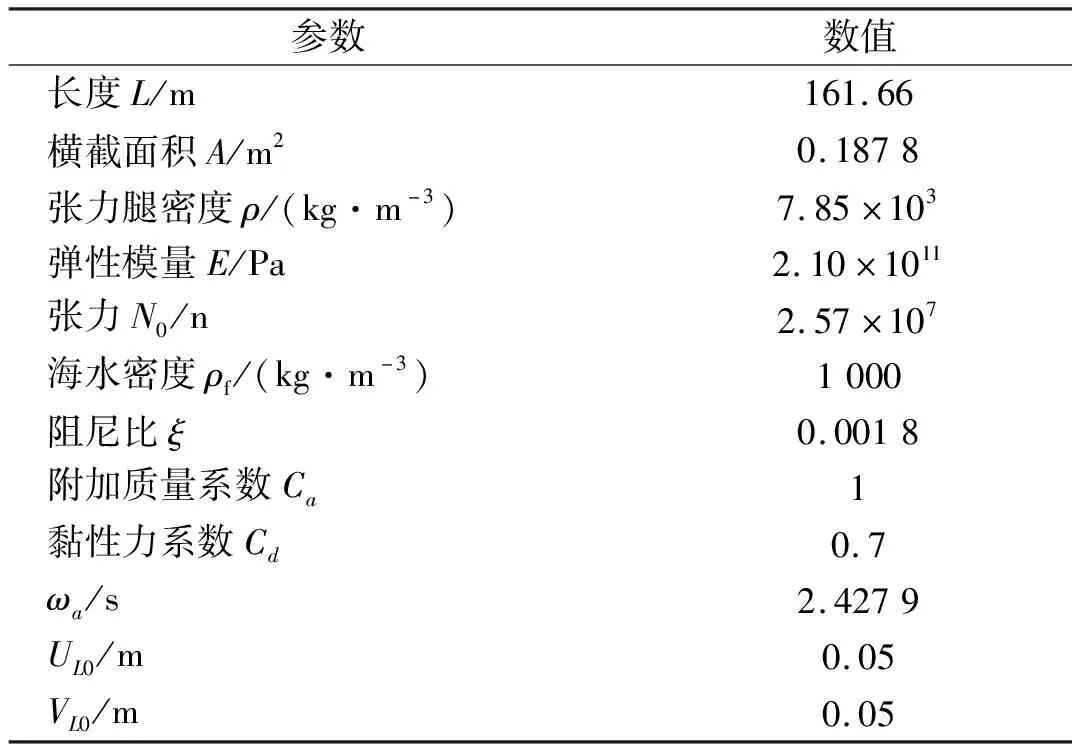
表1 张力腿基本参数

不考虑海流及波浪力对张力腿的作用，通过激励隧道管体间接施加给张力腿，隧道管体的振动频率ωa等于张力腿的第一阶振动频率ω1。图3为张力腿横向前三阶模态位移响应图，图4为张力腿在不同的时间点沿高度变化各点的横向位移变形图。从图中可以看出，张力腿横向运动呈周期性，一阶模态峰值约为0.75 m，且振动响应以第一阶模态为主，取前三阶基本满足计算结果的精度要求。

图3 张力腿横向前三阶模态响应

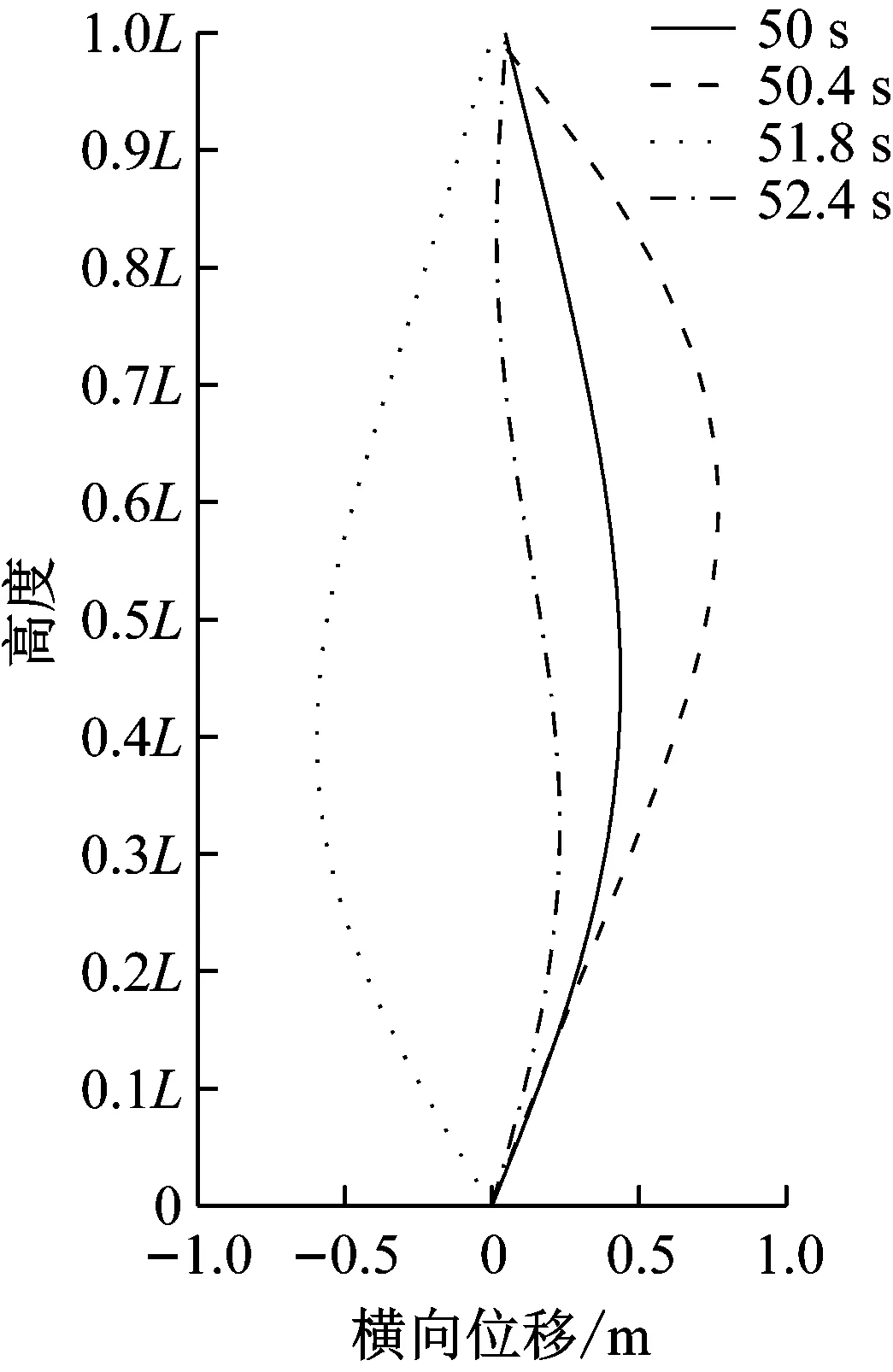
图4 张力腿横向位移变形图

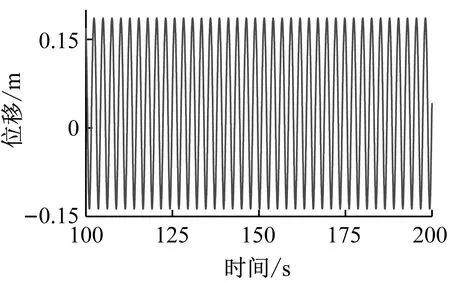
图第一阶模态响应时程曲线和相图

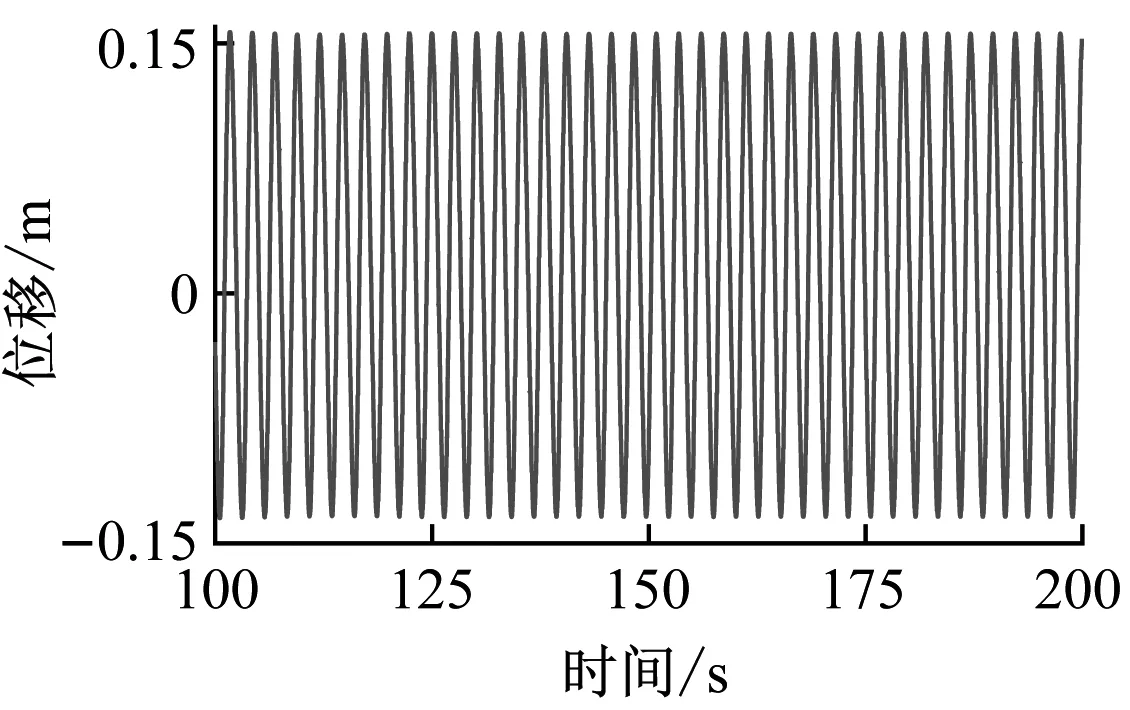
图第一阶模态响应时程曲线和相图

图第一阶模态响应时程曲线和相图

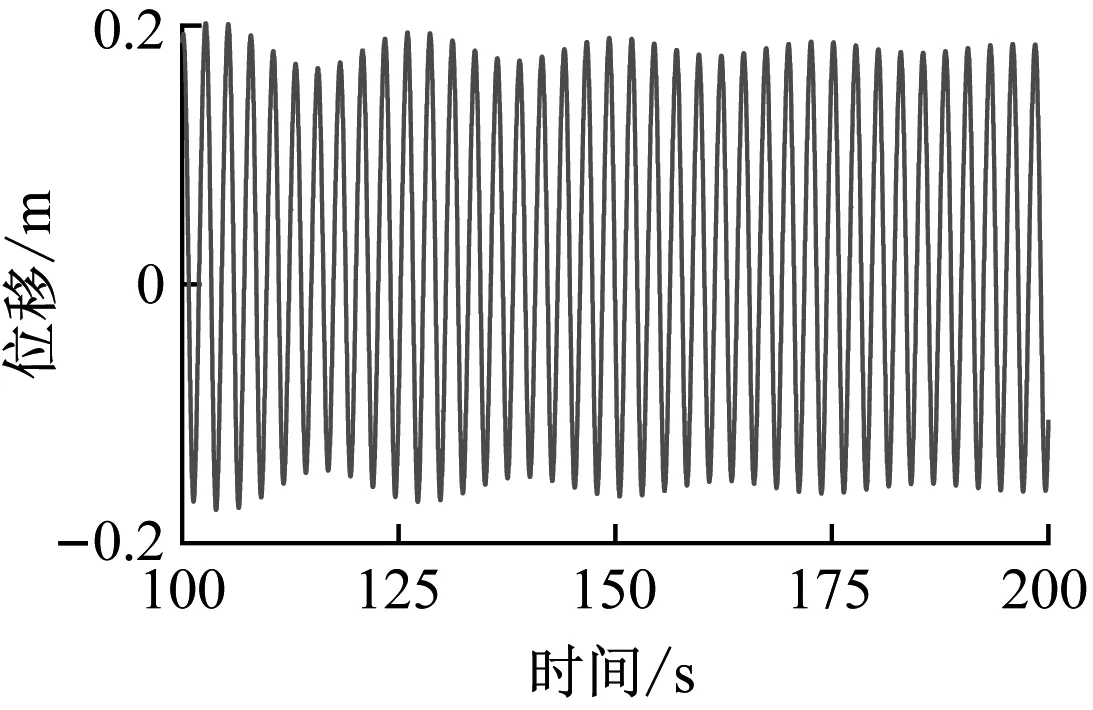
图第一阶模态响应时程曲线和相图

图9为当τ=0.1，xd=L/2时，不同增益下结构的第一阶模态响应时程曲线，如图所示，当时滞量τ为一确定值时，在稳定域内，随着增益量k1值越大，响应幅值越小，故对于某一确定时滞值，通过调节不同的控制增益，可以有效的抑制张力腿的大幅振动越小。图10为当时滞值和增益量固定时，在张力腿的高度分别为L/6、L/4、L/2、5L/8处施加控制力时结构的第一阶模态响应时程曲线，从图可得出，在张力腿中间位置施加控制力时振动抑制效果最好。

图9 τ=0.1时不同控制增益下结构的时程曲线

图时在不同位置施加控制下结构的时程曲线

4 结 论

本文将隧道管体假设成质量点，采用Euler-Be-rnoulli梁理论，分析了时滞速度反馈控制对水下悬浮隧道张力腿的大幅横向振动控制的影响。结果表明，时滞反馈控制能大幅降低张力腿的横向大幅振动，提高结构稳定性，减少其疲劳损坏。并且通过确定稳定域，调节时滞值和增益量为合适值，将控制设置在张力腿中间位置，能使减振效果达到最佳，最高抑制效果可达90%以上；但若时滞和增益量选取不合适，不但达不到控制效果，反而加剧张力腿的振动，并可能出现混沌运动。然而理论模型与实际工程有一定的差距，以后的工作将进一步结合并改进悬浮隧道张力腿设计模型，同时开展相关试验研究，最终将该减振技术在悬浮隧道张力腿中将其实现。