平尾模型连续变速压颤振试验方法及数值计算研究

刘 南，易家宁，王 冬，侯良学，杨希明

(1.中国航空工业空气动力研究院 气动研究与试验二部，沈阳 110034；2.高速高雷诺数气动力航空科技重点实验室，沈阳 110034)

颤振是一种典型的气动弹性不稳定性现象，可能导致飞行器的结构遭到灾难性破坏，在飞行包线内绝对不允许发生颤振现象且留有一定的裕度。风洞试验是研究飞行器颤振问题的重要手段之一，例如我国国军标GJB 67.7A—2008《军用飞机结构强度规范第7部分》[1]中明确要求飞机必须通过颤振风洞试验获得其颤振特性，进而得出颤振设计结论和飞行包线。而跨声速条件又由于流场非线性、颤振速压低、试验风险高，成为颤振风洞试验研究的重点和难点[2]。

相比颤振计算研究[3-5]，目前国内跨声速颤振试验研究主要受到如下两方面的约束：① 国内绝大部分高速风洞都是暂冲式，风洞试验研究大多基于该类型风洞[5-7]，但是暂冲式颤振风洞试验信号有效采样时间短、风洞背景噪声大、信噪比低，而且采用阶梯变速压方式进行颤振试验耗气量大，试验效率低；② 试验模型跨声速颤振边界评估手段不足，基于偶极子格网法的线化方法无法准确预测跨声速颤振边界，一般通过增加安全系数的方式进行处理，结果的精度和可靠性无法保证；而基于雷诺平均Navier-Stokes方程的高精度方法效率较低。

针对上述问题，本文基于自回归滑动平均系统辨识方法建立了一套高效的模型颤振边界预测方法，通过地面振动试验(ground vibration test，GVT)结果对模态数据进行修正后，计算与风洞试验吻合较好，显著地提高了试验的安全性和效率；基于补偿解耦和专家PID建立了高速暂冲式风洞定马赫数连续变速压试验方式，有效地提高了试验效率。

1 试验模型颤振边界高效预测方法

1.1 ARMA辨识方法

首先简单介绍本文采用的ARMA系统辨识方法[8]。该方法中广义气动力预测模型如下：

(1)

式中：fT为广义气动力向量；q为模态位移向量；na和nb分别为输出、输入延迟阶数；k为离散时间步；Ai，Bi∈RN×N为ARMA模型参数，N为模态阶数。

利用3211外部信号作为模态位移的激励，在来流速压QT条件下通过非定常计算得到广义气动力，进而获得时域响应序列{q(k),ya(k)}(k=1,2,…,K)，其中K为迭代步数。通过最小二乘法可以得到矩阵{Ai}(i=1,2,…,na)和{Bi}(i=0,1,…,nb)，具体计算过程此处不再赘述，可以参考文献[9-10]。

将式(1)改写成矩阵形式：

(2)

式中各个量的具体定义可以参考文献[4-5]。

将式(2)转化为连续时域状态空间方程如下：

(3)

结合结构模态运动方程：

(4)

式中：M,D,K分别是广义质量、阻尼和刚度矩阵；q为模态位移，广义力f与fT之间的关系如下：

(5)

式中，Q为来流动压。结合式(3)～(5)可得：

(6)

其中

根据Lyapunov稳定性理论，根据矩阵L的特征值分布能够判断式(6)的稳定性，进而获得试验模型的颤振边界。

1.2 验证算例

利用AGARD445.6机翼对ARMA辨识方法进行验证。该机翼于1961年在TDT风洞进行颤振试验[11]，已成为跨声速颤振研究和程序验证的标准模型之一。

CFD/CSD计算结果(无黏和有黏)、ARMA辨识结果以及风洞试验结果对比如图1所示。由图可见：CFD/CSD计算考虑黏性后，大幅提升与风洞试验结果的吻合度，尤其是Ma=1.041和1.172工况；对于AGARD445.6机翼，ARMA预测结果与CFD/CSD计算结果较为吻合，颤振频率和动压的差别均不超过4%。效率方面，ARMA预测颤振边界仅需一次非定常计算，无需在不同动压下分析时域响应变化趋势，能够显著提升颤振分析效率。

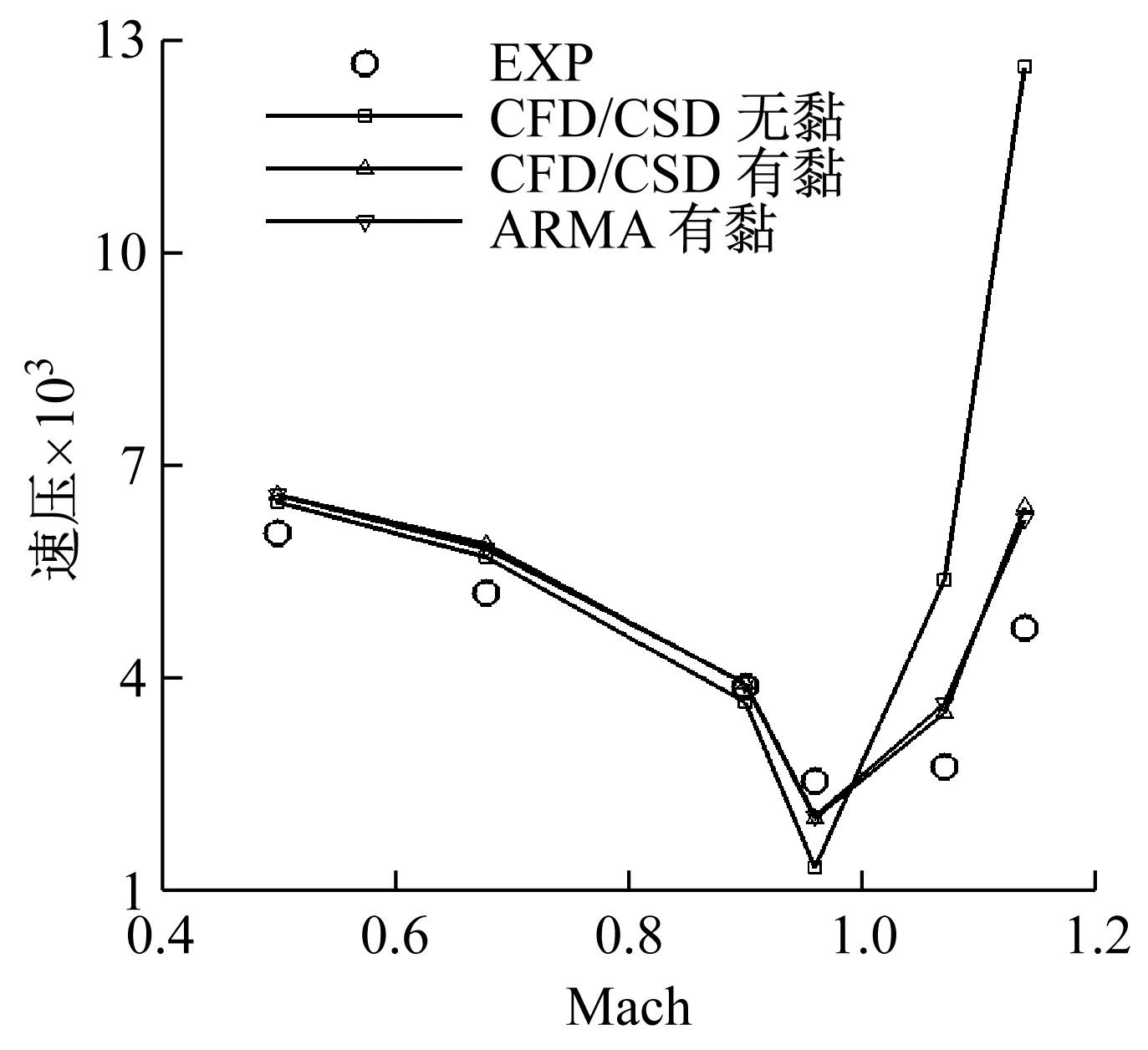
(a)颤振速压

2 定马赫数连续变速压流场控制

FL-60暂冲式风洞流场输入为主调压阀开度、栅指位移和引射器调压阀开度，输出为总压和马赫数。其中引射器用于降低速压运行下限，其运行方式在主调压阀开启前预先调节到特定引射压力，在风洞主管路流场调节过程中，引射压力保持恒定，可视作常量。因此，对于亚、跨声速(Ma=0.4至1.2)流场控制系统可视作两个存在耦合关系的闭环控制回路：① 总压控制回路，以调压阀为执行机构，被控对象是总压；② 马赫数控制回路，以栅指为执行机构，被控对象是马赫数。其中，总压调节过程中阀门开度对马赫数产生耦合影响，马赫数调节过程中栅指位移对总压产生耦合影响。为了消除两者之间的相互影响，首先通过补偿解耦消除耦合影响，然后设计专家PID建立各个控制回路。

2.1 补偿解耦

风洞总压P0和马赫数Ma的参数表达式为

(7)

式中：smv和scf分别是主调压阀开度和栅指位移。由流场调试结果得出，栅指位移对总压的影响近似视作为零，则式(7)可写成如下矩阵形式：

(8)

引入补偿因子并设计反馈解耦器，如下：

(9)

式中：λ12、λ21为补偿因子。若实现完全解耦，则使系统矩阵对角线为0，即

(10)

联立式(9)和(10)，有

(11)

但是风洞流场复杂且具有非线性特征，难以精确得到系统模型参数G11至G22，无法实现完全解耦。在实际工程应用中，往往只需要将耦合作用减弱到一定程度，便可以将耦合视作扰动，通过闭环控制消除耦合影响。

2.2 专家PID控制器

连续变速压试验需要在保证调节速度和调节精度符合需求的前提下尽量避免产生超调，但同一组PID参数的暂态性能和稳态性能相悖，也难以在不同的速压范围内均具备理想的控制效果。此外，风洞流场具有非线性、滞后和时变不确定性等特征，难以获取精确的数学模型。只能将减弱之后的耦合视作扰动，并通过优化控制器性能来消除耦合带来的不利影响。诸多因素使得常规的PID控制器难以满足要求。

FL-60风洞所采用的控制器形式为反馈-前馈结合的符合控制器，其中反馈部分为增量式数字PI控制器，用于稳定被控参数；前馈部分为静态前馈控制器，用于补偿风洞气源压力变化，表达式为

u(k)=u(k-1)+KP[e(k)-e(k-1)]+

KIe(k)+KFFTS

(12)

式中：KFF为前馈补偿系数；Ts为控制周期。

专家PID控制基于受控对象和控制规律的各种知识，根据专家规则、当前状态和历史状态等智能调整PID控制器参数，使受控系统尽可能地优化和实用化，具备一定的自适应性和鲁棒性。

在式(12)的基础上引入各参数的加权因子，则控制算法如下：

u(k)=u(k-1)+αKP[e(k)-e(k-1)]+

βKIe(k)+ξKFFTS

(13)

式中：α、β、ξ分别为比例系数、积分系数和微分系数。

以总压专家PID控制器为例，控制器结构见图2。加权因子的大小由专家系统按照专家规则，根据被控参数的历史输入、输出和其他相关条件进行在线修正。为避免过度修正引起失稳，加权因子取值范围为α,β,ξ∈[0,2]。

图2 风洞总压专家PID控制器

2.3 试验结果

在FL-60风洞开展定马赫数连续变速压流场调试试验，分别在Ma=0.8和1.2工况下进行调试，设定总压变化速率为3 kPa/s，对应速压变化速率分别为0.88和1.2 kPa/s，得到来流总压、马赫数和速压的变化趋势如3所示。由图可见：马赫数控制误差小于±0.003，取得较为理想的控制效果。

3 颤振风洞试验

3.1 试验模型

本文风洞试验采用模型是依据某机平尾为基础，按照FL-60风洞速压运行范围设计得到的缩比模型。几何尺寸如下：展长650.6 mm，翼根弦长659.1 mm，翼根弦长220.3 mm，前缘后掠角34°。结构采用“承力蒙皮+梁”的结构形式，蒙皮、肋板和梁等主要结构形式采用玻璃纤维复合材料，翼根采用高强度铝合金7075材料与转轴连接，内部填充聚氨酯泡沫，翼梢加铅块配重并安装加速度计测量振动响应。

(a)Ma=0.8

开展GVT试验通过锤击法获得试验模型安装在风洞转窗后的固有频率和振型，如表1所示为计算与GVT试验得到的固有频率对比。由结果可见：前四阶固有频率误差均在10%以内，有限元计算与GVT试验符合性较好；但是前两阶固有频率与GVT试验结果存在一定差距，而且这两个模态是颤振主导模态，因此需要在计算前对结构有限元模型进行修正，可以通过修改模型参数匹配GVT测得的固有频率和结构振型。

表1 计算与GVT试验得到固有频率对比(以一阶固有频率计算值为1进行无量纲化处理)

3.2 信号采集和安全防护

试验模型安装在FL-60风洞试验段如图4所示，试验过程中采用PXI动态系统进行振动信号采集，该系统是基于PXI总线的QTS2524动态测试系统，由CM4214放大器、CM4504低通滤波器、NI-PXI4472动态采集设备组成，系统共有24个通道，每个通道动态采样率最高51.2 kHz，动态采集精度0.2%。

图4 试验模型安装在FL-60风洞试验段上

颤振试验数据采集和安全防护软件是基于PXI动态采集设备和Labview软件环境开发的，如图5所示，主要包括操纵面板、采集参数设置以及各个通道的时域响应。其中操纵面板提供人机交互功能，包括开始/停止数据采集、强行关车、显示试验状态等功能，采集参数设置主要供使用人员在试验前设置采样率、各个采样通道、安全防护监控通道和阈值等。

图5 颤振试验数据采集和安全防护软件界面

试验模型安全防护装置如图6所示。试验模型根部安装限位装置，在风洞启动、关车和模型即将发生颤振(连续多次加速度振幅超过预先设定阈值)等条件下，通过气缸驱动限位装置限制模型的扭转位移，从而抑制颤振，保护模型。

图6 试验模型安全防护装置

3.3 试验方法

本文颤振试验通过定马赫数阶梯变速压和连续变速压两种试验方法开展。前者在某个固定马赫数条件下设置若干速压阶梯，每个阶梯保持稳定5～10 s并记录模型的振动信号；后者则是在某个固定马赫数条件下速压线性增大。试验结束后，通过亚临界响应分析方法分析振动信号，并外插得到颤振边界。

本文亚临界响应分析方法选择Peak-Hold方法，该方法在国内外高速颤振风洞试验中得到广泛应用[12]。其原理如下：对于弹性系统置于风洞气流中受到湍流激励，系统的振幅可以表示为颤振微分方程的解，表示如下：

(14)

式中：Q为广义力；A为广义气动力(是马赫数和减缩频率的函数)；V为来流速度；ρ为来流密度；下标f、s和t分别代表颤振、振动和湍流。

对上式左右两边求倒数，并将振动和湍流项分开，对于湍流激励可得：

(15)

因此，当系统接近颤振临界点时，1/|a|与速压接近线性关系，因此可以利用谱峰值倒数进行颤振边界外插。

3.4 试验结果分析

针对颤振风洞试验结果，首先将流场和翼梢加速度时域响应(由于加速度信号信噪比较低，本文利用低通滤波器已将200 Hz以上的高频信号滤除)分段加窗，如图7所示，然后计算各段的平均速压及对应的加速度频谱，画出谱峰值随速压的变化趋势及其拟合曲线如图8所示，预测得到颤振边界43.0 kPa，其中图8(a)是3车阶梯变速压试验结果的综合展示，试验过程中每车最多3个速压阶梯。

(a)马赫数和速压

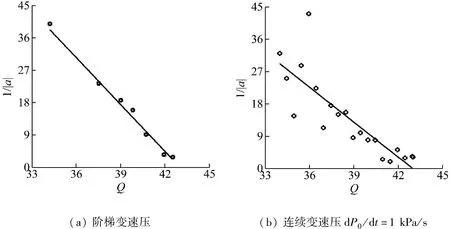
图8 谱峰值倒数随速压的变化趋势及拟合得到的线性趋势线(Ma=0.70)

综上，通过本次试验分别获得两种试验方式得到的平尾模型颤振边界如表2所示。结果表明：两种试验方式得到的颤振边界非常接近，差别不超过2%。

表2 平尾模型两种试验方式得到的颤振速压对比

3.5 颤振边界对比

颤振速压边界计算与试验结果对比如图9所示，由图可见：利用原始有限元模型进行颤振分析得到的颤振边界较高，利用GVT试验结果对有限元模型修正后得到颤振边界与试验值较为吻合。

图9 平尾模型颤振速压和频率对比

由本文结果可见，对于一般的部件级颤振模型，通过数值计算在风洞试验前可以得到较为可靠的颤振边界。如果采用定马赫数阶梯变速压试验方式，根据计算结果在来流速压远低于颤振速压时，可以适当增大速压阶梯，在靠近颤振边界时适当减小速压阶梯。如果采用定马赫数连续变速压试验方式，可以进一步改进设计分段线性速压变化流场控制程序，在来流速压远低于颤振速压时，可以适当增大速压变化速率，在靠近颤振边界时适当减小速压变化速率。

4 结 论

针对跨声速颤振裕度低、风险高、预测难度大的问题，本文建立了一套高效高精度颤振预测方法和连续变速压试验方法，得出结论如下：

(1)首先建立了基于CFD/CSD耦合的高精度颤振预测方法，但是该方法需要在时域内求解非定常流场和结构运动方程并且反复迭代，效率极低，在此基础上，建立了基于ARMA系统辨识模型的高效颤振预测方法，每个马赫数条件下仅需进行一次非定常计算即可，效率提升一个量级左右；

(2)通过AGARD445.6标模对CFD/CSD耦合计算方法和ARMA辨识方法进行验证，计算结果与试验吻合度很高；

(3)基于FL-60风洞建立了定马赫数连续变速压试验能力，通过流场调试证明速压变化线性度高、马赫数偏差小(波动范围小于±0.003)；

(4)通过平尾模型对上述成果进行综合验证，阶梯变速压和连续变速压两种试验方式颤振速压差别低于2%，计算结果与试验吻合度较好，为试验车次安排可以起到良好的指导作用。

以上试验模型的设计结果固有频率和结构振型与GVT试验有一定差别，后续针对上述差异进一步研究，探索复合材料有限元分析、铺层设计和加工工艺等影响；该试验模型的跨声速凹坑附近颤振速压过低，无法通过暂冲式风洞试验获得，后续通过修改模型或改至连续式风洞(可负压运行)进行试验，获得较为完整的颤振边界，为数值计算验证提供更加丰富的试验数据。