基于深度学习的单自由度机械臂定位可靠性估计

鲍 丹，侯保林

(南京理工大学 机械工程学院，南京 210094)

随着机器人技术的发展，机械臂被广泛应用于工业制造、航天航空、医学治疗和军事等各个领域，比如物流系统中用于搬运、包装的机械手；航空航天的空间自由漂浮机械臂；火炮自动装填系统中的弹药传输机械臂。机械臂定位可靠性是动作可靠性的一种，它表示机构在规定的实用条件下，在规定的使用期内，为实现其规定功能，而使其性能保持在允许值范围内，能精确、及时、协调地达到目标位置的能力。但是，由于受工作环境的影响，在运动过程中的机械臂系统受到不确定性参数和外部扰动等因素的影响，使其定位可靠性的估计很困难。因此，研究机械臂在参数不确定以及存在外部随机扰动的情况下的定位可靠性具有重要意义。

国内外目前也有大量对系统中存在不确定性参数的可靠性问题研究。例如，Rao等[1]使用概率方法对机械手运动学和动力学进行建模，在此基础上提出计算可靠性的方法；Kang等[2]基于概率多椭球凸集混合模型，提出了在参数不确定或载荷不确定情况下结构安全可靠度指标的数学定义；姜潮等[3]针对系统中既有概率变量又有区间变量的混合不确定问题提出了一种概率-区间混合结构可靠性的高效计算方法；孟广伟等[4]提出了借助降维方法将功能函数利用泰勒展开，推导结构功能函数的前4阶中心距，利用四阶矩法分别获得失效概率上界和下界；邱涛等[5]针对机械结构中既有随机变量又有区间变量的混合可靠性问题，提出一种基于二参数的混合可靠性分析算法。上述文献的方法是基于功能函数可用显式数学方程表达，当系统受到随机扰动的影响，复杂性增加，显式方程难以获得时，采用神经网络模型是可取的选择。例如文献[6]建立神经网络代替位置分量的动力学模型，结果表明该方法能较好地满足计算精度的要求；朱坚民等[7]针对机床滑动结合面动态特性参数不确定的问题，结合神经网络对参数进行优化辨识；高学星等[8]构建了基于径向基神经网络的代理模型以提高计算效率，实现弹药协调器动作可靠性估计。

具有单隐层的前馈神经网络足以表示任何一个函数，但是当函数的非线性特别强时，则需要非常多的隐层单元，不仅大大降低计算效率，更有可能无法正确地学习和泛化。针对非线性复杂系统，使用更深的网络模型能够减少隐层单元数量，并且可以减少泛化误差[9]。因此，文章提出了一种基于深度学习多隐层结构的神经网络模型结合LM(levenberg-marquardt)算法，用于估计机械臂的定位可靠性。在ADAMS中建立机械臂系统的不确定模型，区间不确定参数在一次动作过程中可视为定值，通过实验数据结合参数辨识的方法辨识出几组实验的参数，同时验证单自由度机械臂仿真模型的准确性；在模型中加载外部随机扰动，对区间不确定性参数进行拉丁超立方采样，将每一组参数带入模型，获得机械臂在运动中的定位误差，从而得到样本数据；然后构造基于LM算法的深度学习神经网络的模型，基于此模型估计机械臂定位可靠性。最后通过多组实验数据分析表明文章提出的定位可靠性估计方法具有高效性和有效性。

1 单自由度机械臂模型建立

1.1 单自由度机械臂不确定性参数分析

文章研究的单自由度机械臂是以某火炮的弹药传输机械臂为原型。单自由度机械臂由电机、控制器、减速箱、机械臂、气弹簧、台架、负载以及振动台组成，主要实现机械臂末端负载的准确定位。控制器与上位机进行数据交换，通过电流控制电机的转矩，电机输出转矩经过行星齿轮减速箱实现单自由度机械臂的绕轴运动，系统结构如图1所示。气弹簧用于平衡机械臂的重力矩，减小电机的负载。

图1 单自由度机械臂的结构示意图

单自由度机械臂系统中包含众多参数，其中某些参数是可以通过计算或测量的方式获得，如等效转动惯量，机械臂物理尺寸；某些参数是不确定的，在估计单自由度机械臂的定位可靠性的时候，考虑工作时间段中外部环境的变化(例如温度，气压等)和零件的磨损变形，这类参数在长时间工作中是变化的，只能确定其变化的范围。对于文章研究的机械臂系统而言，这类区间不确定性参数包括：减速箱传动效率η，气弹簧的初始压力p和气体的多变指数n。

(1)减速箱传动效率η；由于齿轮间的润滑条件和长时间的使用等因素使减速箱的传动效率受到影响，将这些因素对整个传动系统性能的影响等效在减速箱传动效率η上。

(2)气弹簧的初始压力p；气弹簧的初始压力随着外部环境的变化而变化，在此气弹簧的初始压力被视为变化的区间不确定参数。

(3)气体的多变指数n；气弹簧的伸缩杆在运动过程中，气体的多变指数受外部环境温度影响，是变化的不确定性参数。

1.2 单自由度机械臂不确定性建模

在仿真软件ADAMS中建立了单自由度机械臂的动力学模型和控制模型。模型的控制采用PID控制，PID控制器由比例单元(P)、积分单元(I)和微分单元(D)组成，结构和算法简单，应用广泛，工业过程控制中95%以上的控制回路都具有PID结构。在建模过程中，对三个不确定性参数进行参数化区间建模。并采用MATLAB程序控制参数化仿真，即在改变不确定性参数的取值，自动进行仿真，得到相应参数下的机械臂角位移变化曲线，以便后面参数辨识过程中的大量仿真的自动进行。

根据实际经验、器材说明书以及相关文献[10]，确定三个区间不确定参数的变化区间分别为：减速箱传动效率η为[0.58,0.63]；气弹簧的初始压力p为[0.46,0.52]，单位MPa；气体的多变指数n为[1.08,1.26]。

1.3 参数辨识与模型验证

系统的三个区间不确定性参数在长时间内是变化的，但在机械臂一次动作定位过程中，由于时间极短可近似看作是定值。利用实验数据对系统参数进行辨识，同时验证ADAMS动力学模型的准确性。图2为测试过程的图片。在无负载情况下进行三次机械臂的重复性定位测试，以20°为目标定位位置，得到图3 所示的三组机械臂角位移变化曲线。在加载负载的情况下进行三次机械臂的重复性定位测试，仍以20°为目标定位位置，得到图4所示的三组机械臂角位移变化曲线。

图2 测试照片

图3 无负载时角位移变化测试结果

图4 有负载时角位移变化测试结果

文章的辨识问题可看成一个优化问题来解决，即在控制条件与测试过程中的控制参数一致的情况下，当减速箱传动效率、气弹簧的初始压力和气体的多变指数在区间中变化时，在区间内找到一组最优的参数，使得仿真得到的机械臂角位移曲线与测试所得的角位移曲线相似度最高。以时间序列曲线相似度为优化目标，文章采用动态时间规整(DTW)[11]计算仿真曲线与测试曲线的相似度来评价辨识结果。寻优过程采用粒子群优化算法，粒子群优化算法(particle swarm optimization, PSO)以其实现简单、精度高、收敛快等优点被广泛运用，它是从随机解出发，通过迭代寻找最优解，并通过适应度值来评价解的优劣[12]。PSO参数包括种群规模m、最大迭代次数N、惯性权重、学习因子c1和c2，粒子位置和速度的范围。优化问题的自变量值即为粒子的位置，在每一次迭代中，粒子通过跟踪两个极值(个体极值和群体极值)，再根据以下公式来更新位置和速度直到满足结束条件。其中x表示粒子的位置，v表示粒子的速度；d表示不确定参数的个数；pid表示个体极值，pgd表示群体极值；r1和r2为[0,1]范围内的均匀随机数，k为迭代次数。

vid(k+1)=wvid(k)+c1r1(pid-xid(k))+

c2r2(pgd-xid(k))

(1)

xid(k+1)=xid(k)+vid(k+1)

(2)

粒子群算法的流程图如图5所示，具体步骤为：

图5 PSO算法流程图

(1)初始化粒子群的位置和速度，设置种群规模、最大迭代次数，惯性权重，学习因子等参数。

(2)计算每个粒子的适应度值(此处的适应度值为时间序列曲线相似度)。

(3)将每个粒子的适应度值与个体极值进行比较，更新个体极值；将每个粒子的适应度值与群体极值进行比较，更新群体极值。

(4)根据式(1)和式(2)更新粒子的位置和速度。

(5)如果满足结束条件(达到精度或者达到最大迭代次数)则退出，否则返回步骤(2)。

由于实际系统待辨识的参数是难以测量的，文章利用仿真模型实验来确定此方法的辨识精度，再利用测试数据对单自由度机械臂的参数进行辨识，来验证仿真模型的准确性。表1给出了辨识结果。其中，通过仿真模型，粒子群算法对三个待辨识参数辨识结果的平均相对误差分别为0.54%、2.48%和0.61%，可见辨识精度较高，满足实际需求。对于图3中的无负载情况下的3组测试数据，通过辨识的方法分别得到3个待辨识参数的辨识值；对于图4中的有负载情况下的3组测试数据，通过辨识方法分别得到3个待辨识参数的辨识值，且辨识值均与理论值相符。将有无负载情况下的第二组辨识结果带入仿真模型，计算得出机械臂角位移辨识结果与测试数据进行对比，如图6所示，从图中可以看出，两组对比的相似度均很高，表明辨识结果是合理的，并且仿真模型是准确的。

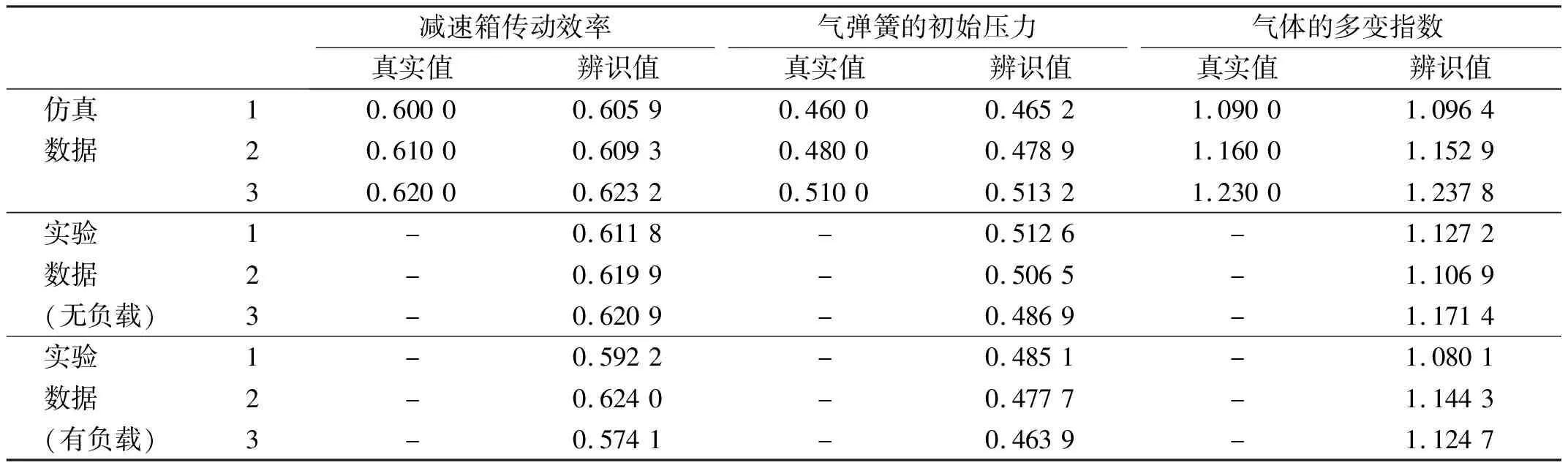
表1 辨识结果

(a)无负载情况

与测试过程一样，在三个位置采用正弦波叠加原理加载随机外部扰动，振动台由三个振动柱构成，每个振动柱加载随机正弦波位移扰动。在仿真模型中，正弦波的频率均为1 Hz，幅值在区间[0,30]中随机取值，单位mm;相位在区间[0,180]中随机取值,单位为度。当幅值分别为7 mm、18 mm和30 mm,相位取值分别为45°、90°和180°时，三个振动柱加载的位移扰动如图7所示。

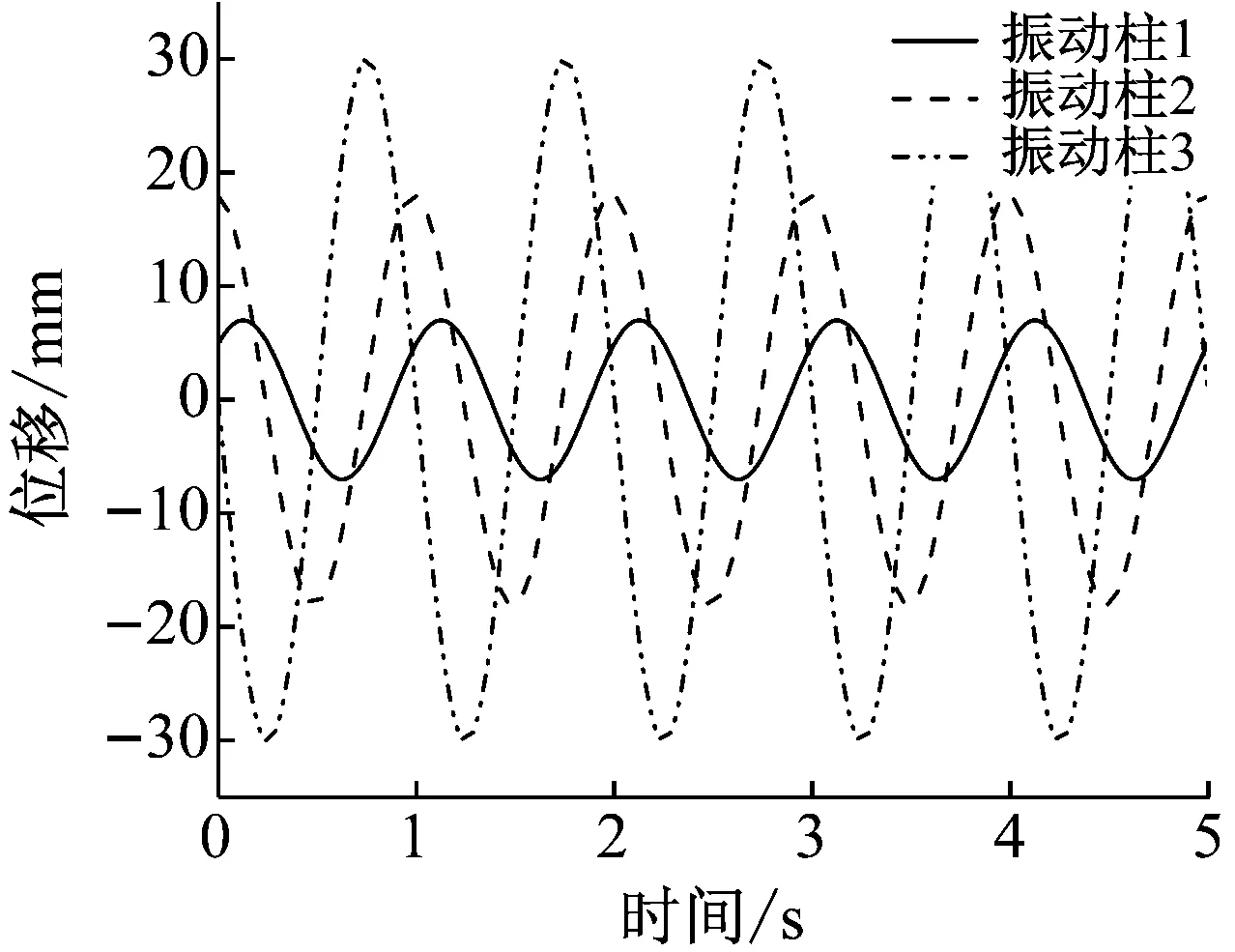
图7 随机扰动信号

在三个不确定参数的区间内进行拉丁超立方采样10 000组，将每一组参数带入仿真模型，机械臂在随机外部扰动中实现定位，从而获得机械臂定位误差。不确定性参数作为训练深度学习神经网络模型的输入，机械臂定位误差作为其训练的期望值。

2 深度学习神经网络模型建立

2.1 深度学习神经网络结构

进行可靠性计算时，需要大量的数据，通过实验获得大量数据是耗时耗力不可取的。并且在文章所研究的机械臂系统中，存在着多个区间不确定参数，所以文章采用了基于深度学习的代理模型来分析机械臂系统的可靠性。深度学习是机器学习的一种方法，它大量借鉴了我们关于人脑、统计学和应用数学的相关知识[13]。深度前馈神经网络也称多层感知机，是典型的深度学习模型，主要包含输入层，隐含层和输出层，如图8所示。神经网络是由大量的神经元连接而成的复杂网络，其中“M-P模型”是一直沿用至今的神经元模型。在这个模型中，每个神经元接收到前一层所有神经元传递过来的输入信号，这些信号通过权重的连接进行传递，再经过偏置，然后通过“激活函数”处理产生神经元的输出，并传递到下一层神经元。

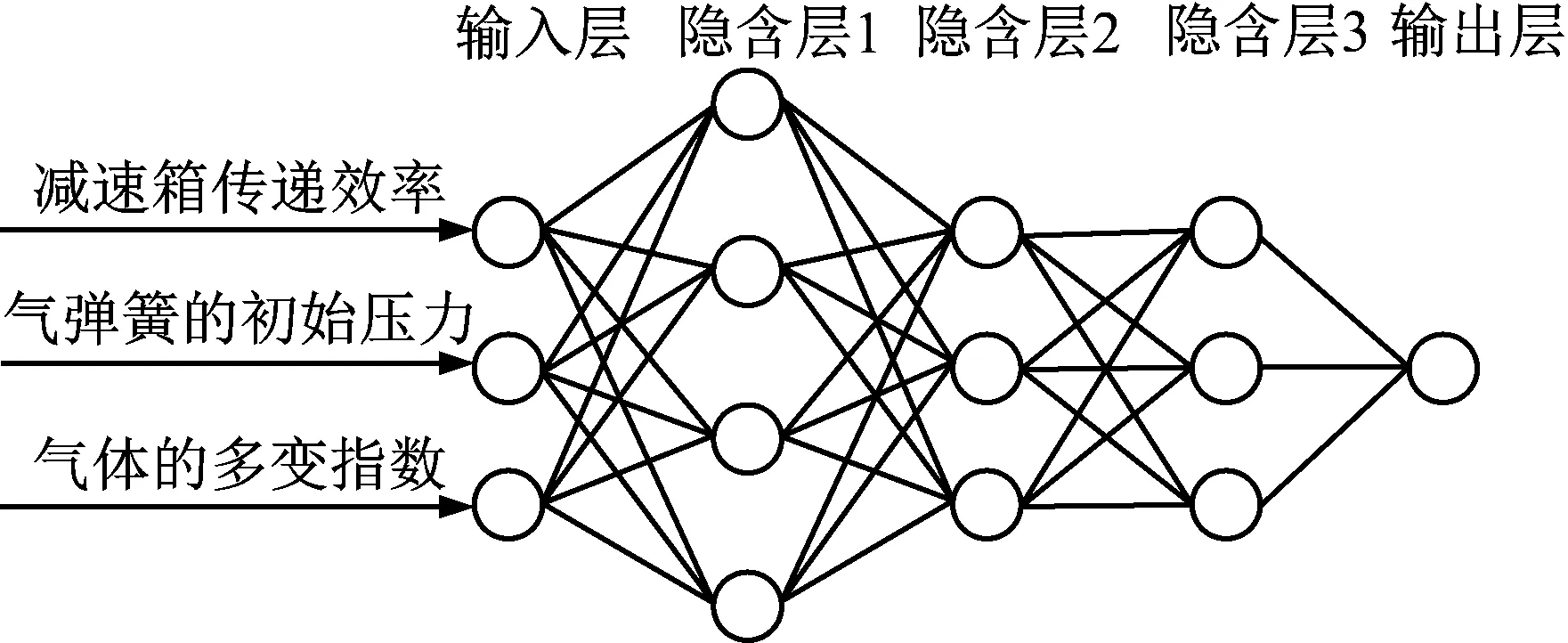
图8 神经网络模型结构

图9 M-P神经元模型

(3)

(4)

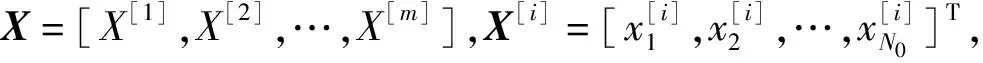
(5)

根据文章有三个输入，一个输出，采用含三个隐含层的神经网络结构，则W(1)为4×3的矩阵，b(1)为4×1的矩阵，W(2)为3×4的矩阵，b(2)为3×1的矩阵，W(3)为3×3的矩阵，b(3)为3×1的矩阵，W(4)为1×3的矩阵，b(4)为1×1的矩阵。

2.2 基于Levenberg-Marquardt算法的模型

神经网络的训练过程就是根据输出与期望输出之间的误差来调整神经元之间的权值以及阈值，使得预测输出与期望输出最接近。文章采用LM算法[15-16]来更新权值和阈值。LM算法是介于梯度下降法和高斯牛顿法的一种非线性算法，在远离最优解的时候，它具有梯度下降法的全局搜索特性，在接近最优解的时候，LM算法具有高斯牛顿法的局部快速收敛性。LM算法的权值和阈值更新准则为：

(6)

(7)

(8)

(9)

式中，下标k和k+1分别表示当前迭代和下一迭代，Jk是神经网络输出误差相对于神经网络权值的雅可比矩阵，Ek是由目标系统与神经网络输出误差组成的误差向量。第l层权值和阈值的雅可比矩阵可由公式(8)和(9)得到。μ是LM算法中的超参数，当μ值很小的时候，LM算法近似于高斯-牛顿法，当μ值很大的时候，LM算法近似于梯度下降法。这里μ采用自适应算法。

设置神经网络的相关参数：神经网络具有三个隐含层，第一层含有4个神经元、第二层和第三层分别含有3个神经元；采用正态概率分布法采样初始化权重和阈值，平均值为0，标准方差为前一层的节点数的开方；最大迭代次数为1 000次。

采用LM算法训练神经网络，得到模型预测结果，并与单隐层神经网络的预测结果进行对比，图10为单隐层结构且含有10个神经元的网络模型预测误差，单隐层结构且含30个神经元的网络模型预测误差以及文章提出的多隐层结构且含10个神经元的网络模型预测误差对比图，它们的平均预测误差分别为0.107 5、0.092 0和0.051 7。当神经元数目相同时，多隐层结构神经网络的预测精度比单隐层神经网络的预测精度高两倍。此外，由图11可得，基于LM算法的深度学习神经网络模型收敛速度更快。因此，文章的机械臂定位可靠性分析是基于LM算法的深度学习神经网络模型。

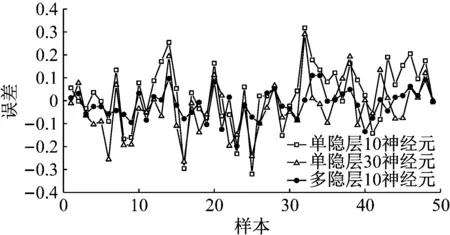
图10 不同神经网络模型预测误差对比图

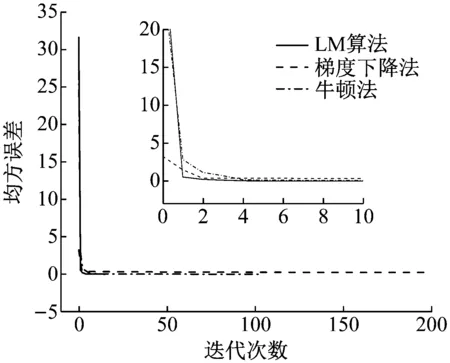
图11 不同算法下模型的收敛速度

3 定位可靠性分析方法与结果

3.1 定位可靠性的分析方法

定位可靠性是动作可靠性的一种，它表示机构在规定的实用条件下，在规定的使用期内，为实现其规定功能，而使其性能保持在允许值范围内，能精确、及时、协调地达到目标位置的能力。定位可靠性取决于系统的物理参数、几何参数、边界条件和外部载荷等，设这些因素为系统的随机变量X=(x1,x2,…,xn)，每一组随机变量经过系统得到对应的定位误差，即定位误差Y是随机变量的函数。

Y=g(X)=g(x1,x2,…,xn)

(10)

在正常运动的系统中，如果任一定位误差超过某一临界状态将不能满足设计指标，这一临界位置称为系统的极限状态。对于机械臂定位可靠性问题，极限状态函数可表示为

f(X)=Y0-Y

(11)

式中：Y为随机变量X下的定位误差，Y0为要求的误差范围。动作是否可靠可以通过f(X)来判断。如果能将f(X)表示为X的明确数学表达式，则称之为显式极限状态函数，否则称为隐式极限状态函数。在实际工程中，难以获得不确定参数的概率密度分布；另外，由于存在外部随机扰动，使得机械臂的定位误差极限状态函数f(X)很难用明确的数学表达式来表示；并且，可靠性分析需要进行成千上万次不停随机变量下的模拟计算，从时间上来说也是不现实的。文章采用上述基于深度学习的神经网络代理模型进行定位可靠性估计。

定位可靠性计算流程如图12所示。前处理模块主要完成机构动力学模型不确定性参数辨识和模型验证，对区间不确定参数采样，并产生随机扰动，带入动力学模型来获取用于训练深度学习模型的样本点。机械臂的定位误差作为训练样本的输出。由于涉及大量的重复仿真操作，整个流程采用脚本程序自动完成，主要包括的步骤有调用MATLAB自动修改ADAMS参数文件，打开动力学软件完成参数赋值并进行仿真，保存仿真结果。中间处理模块主要以区间不确定参数为输入，定位误差作为输出建立深度学习神经网络模型。后处理模块完成对基于深度学习神经网络模型的大量仿真结果进行统计，利用蒙特卡洛算法最终计算出定位可靠性。

图12 基于深度学习模型和蒙特卡洛的定位可靠性计算流程

3.2 定位可靠性的估计结果

根据3.1的定位可靠性计算流程，进行可靠度的估计。在一次动作过程中，机械臂从初始位置0°运动到定位位置，设置20°为目标角位移，定位误差为机械臂协调的定位角度与目标位置的角度之差。通过深度学习神经网络模型，模拟106组数据。采用蒙特卡洛算法得到定位误差绝对值的概率密度分布以及定位误差绝对值的累积概率分布，如图13和图14所示。该机械臂的定位误差精度指标为0.5°，仿真可得机械臂的定位误差绝对值不超过0.5°的概率是84.12%，即机械臂的定位可靠性为84.12%。最后在不同的环境温度中进行了100组实验，得到100组机械臂的定位误差，如图15所示。对100组定位误差进行分析，可得机械臂的定位误差概率为82.05%。仿真结果与实验结果很接近，且仿真所得误差绝对值的累计概率分布与实验测试所得的误差绝对值累计概率密度曲线重合度很高，如图14所示。

图13 定位误差绝对值概率密度分布

图14 定位误差绝对值累计概率分布

图15 100组实验的定位误差

4 结 论

文章建立了单自由度机械臂的动力学模型和控制模型，根据实验数据辨识系统中的参数并验证了仿真模型的准确性；针对系统中存在区间不确定参数以及随机扰动的因素，使得系统复杂性和非线性急剧上升，提出了一种基于深度学习结合Levenberg-Marquardt算法的神经网络模型来估计定位可靠性；对神经网络模型进行Monte-Carlo仿真分析后，求解了定位误差的概率分布，机械臂的定位可靠性估计值为84.12%。最后通过100组实验的数据分析，表明文章提出的方法具有可行性，这为复杂系统的可靠性估计提供了借鉴。