基于声波衰减模型对液体管道泄漏位置的极大似然估计

2021-08-11池招招蒋军成王志荣沈国栋郝永梅

振动与冲击 2021年15期

池招招，蒋军成,，刁旭，倪磊，王志荣，沈国栋，郝永梅

(1.南京工业大学安全科学与工程学院，南京 211816；2.常州大学环境与安全工程学院，江苏常州 213164)

随着我国工业化进程的加快和能源结构优化的推进，我国油气管道建设正迎来一个大的发展机遇期。虽然油气管道运输为经济发展带来诸多便利，但是油气管道安全影响因素多，部分因素偶发性强，运行风险高，管理难度大[1-3]。油气管道泄漏可能导致爆炸等严重事故，造成巨大的生命财产损失和环境问题。因此泄漏检测方法的研究将有助于提升我国油气集输系统安全保障的技术水平，具有重要的经济价值和社会意义。

针对管道泄漏定位研究，Li等[4]通过对信号使用时频分析谱(crosstime-frequency spectrum，CTFS)去噪，然后通过互相关分析确定上下游传感器接收到泄漏信号的时差，使用时差法对泄漏点进行定位，所得结果相较单纯时差法误差降低六倍。Liu等[5]研究了声波在管道上的传播衰减公式，并对该公式进行修正，通过实验获得管道上下游处声波幅值，使用声波衰减公式计算得到泄漏点位置。该方法与时差法相比，无需获得声波传播波速和上下游传感器接收到泄漏信号的时差，且Liu等将该方法成功应用到实际油气管道上。Sun等[6]仍旧使用时差法进行泄漏定位，但不同点是使用了威格纳-维尔分布(wigner-ville distribution，WVD)计算时频参数，并通过时频参数获得时差。Sun等是将时差法用于声发射(acoustic emission, AE)信号，Liu等[7]则是在压力信号中使用时差法。Liu等[8]使用了改进之后的小波包对动态压力传感器获取的信号进行去噪，并对比时差法与幅值衰减法的定位情况，结果表明幅值衰减法定位结果优于时差法，且不受时间测量与波速测量装置的限制。

由于管道中液体流动的影响，上下游衰减参数是有差异的；使用声波衰减公式定位时，若工况发生变化，则需要重新计算衰减参数。本文针对上述问题改进了衰减参数的设置，分别计算上下游参数值；且为了避免每次计算衰减参数前需要确定管道运行参数，改进了传感器的布设方式，直接通过实验数据获得衰减参数值，然后使用极大似然估计(maximum likelihood estimation, MLE)法对改进后的衰减公式进行变换并求解，从而获得预测的泄漏位置。

1 原理

1.1 声波衰减模型

泄漏状态下，流体从泄漏口喷射至管外时，液体与管壁相互作用产生声发射源，声发射源向外辐射能量形成压力波并以波速沿着管壁进行传播。通过在管壁上安装AE传感器则可记录得到声波信号。

声波信号随传播距离的增加而发生的衰减公式[9]为

p=p0e-σαx

(1)

式中：x为声波传播距离，m；p0为泄漏点处的声波幅值，Pa；p为相应传播距离x处的声波幅值，Pa；σ为修正系数，用于修正管道运输不同介质时所产生的差异，对于水管，取值3～4，而对于气体管道则是0.5～1.5；α为黏热吸收系数，用于表征由于黏性吸收和热传导所造成的声波强度衰减，根据公式(1)可知，α值越大，黏性吸收和热传导对声波的衰减作用越强，α计算公式为

α=αη′+αη″+αχ=

(2)

式中[10]：αη′为切变黏滞吸收系数;αη″为容变黏滞吸收系数；αχ为热传导吸收系数；ω为角频率，rad/s，ω=2πf；f为声波频率，Hz；r为管道内径，m；ρ0是介质密度，kg/m3；c0为声波在管道中的传播速度，m/s；η为动力黏滞系数，Pa·s；η′为切变黏滞系数，Pa·s；η″为容变黏滞系数，Pa·s；χ为热传导系数,W/(m·K)；Cv为定容比热；Cp为定压比热,kJ/(kg·K)。

若是按照传统的声波衰减定位方法，则需要根据管道运行状态确定上述所有参数，从而获得黏热吸收系数α。当所需检测的管道发生变化时，其对应的r，c0，η′，η″，χ相应地也需要做出调整，而当管道内介质发生变化时，需要相应调整ρ0，Cv和Cp，这就造成了计算上的繁琐以及变换应用场合之后的重复计算。

因此本文在该基础上，增加了上下游衰减系数的差异性；且改变了传统的传感器布置方式，以便于σ和α的计算，传感器布置示意图如图1所示。

图1 水管泄漏声波检测的传感器布置示意图

按照式(1)可知，对于水管修正系数σ取值为3～4，只给出取值范围而没有确切的数值，所以本文为了避免修正系数取值的差异对结果的影响，将修正系数σ和黏热吸收系数α合并，在本文中两系数乘积σα即为声波衰减系数。

根据式(1)，声波向上游点1和点2的传播公式为式(3)和(4)，上游的衰减系数为σ1α1

p1=p0e-σ1α1x1

(3)

p2=p0e-σ1α1x2

(4)

同理，声波向下游点3和点4的传播公式如式(5)和式(6)，下游的衰减系数为σ2α2

p3=p0e-σ2α2x3

(5)

p4=p0e-σ2α2x4

(6)

式中，p0为泄漏点处的声波信号幅值，mV。(式(1)的声波为压力值，而实验设备所得幅值为电信号的电压值，本文直接使用电信号的电压值代替声波压力值)；x1，x2，x3和x4分别为传感器1，2，3，4与泄漏点之间的距离，m；p1，p2，p3和p4分别为传感器1，2，3，4所获取的声波信号幅值，mV；σ1α1可由上游两个传感器的幅值比值获得，即式(3)除以式(4)

(7)

变换公式获得

(8)

同理可得

(9)

(10)

从上式可以看出，只要知道声发射传感器在测量点1、2、3、4处的声波信号幅值p以及同一端传感器之间(1和2之间，3和4之间)的距离，即可由式(8)和(10)获得衰减参数的数值。

1.2 声波衰减模型的极大似然估计

公式(8)和(10)仅能得到σα的值，如果使用衰减公式(1)计算x，则需要知道泄漏点处的声波幅值，但是实际工程应用中，泄漏点处的声波幅值是无法得到的，仅仅用该公式并不能得到泄漏位置。所以对于泄漏位置的预测，本文在声波衰减公式的基础上采用MLE。MLE的估计流程图如图2。

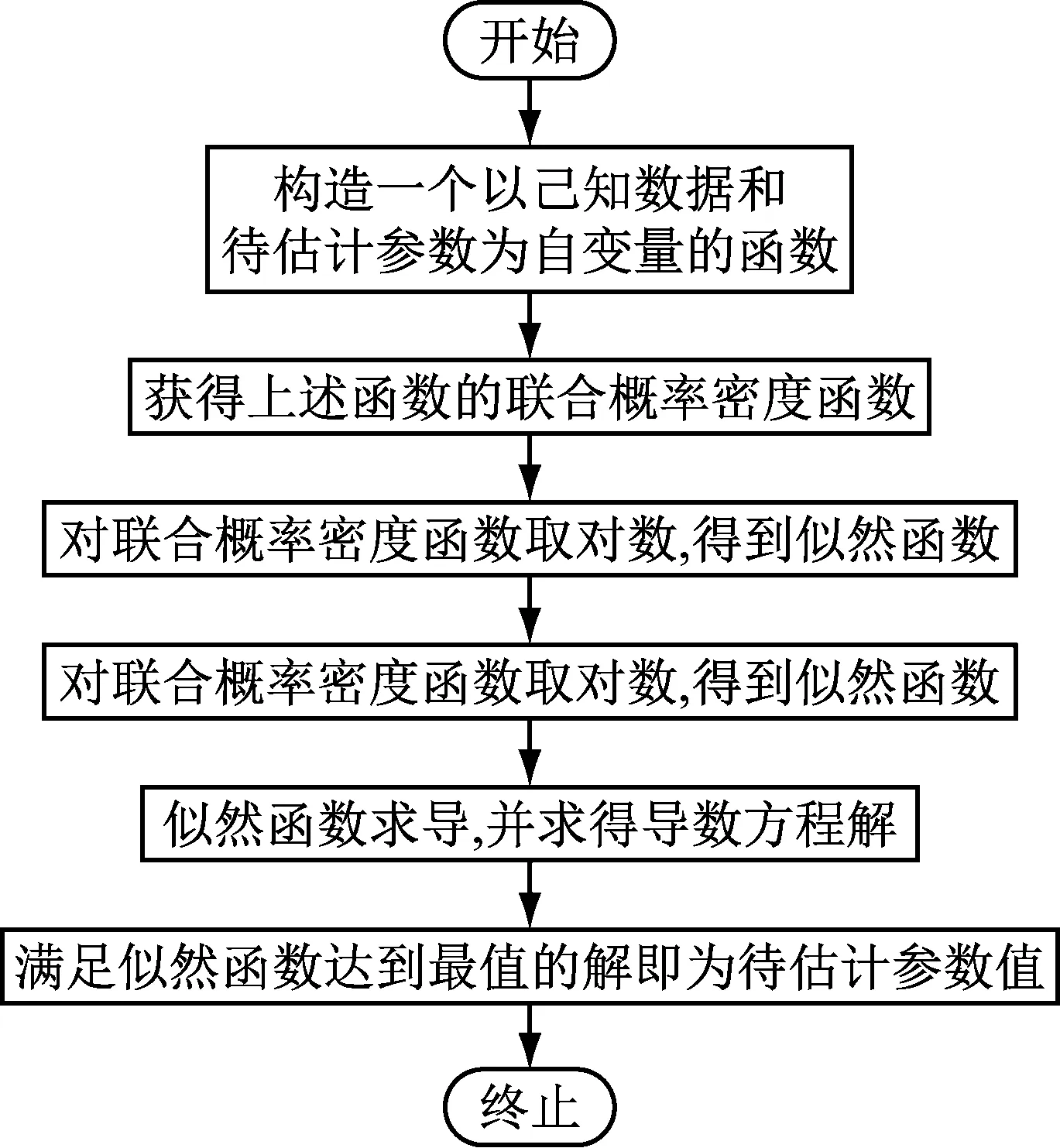
图2 MLE流程图

按照上述流程，首先定义一个上下游的幅值比值公式为

(11)

由于泄漏检测过程中，信号常常夹杂着噪声，所以本文在公式(11)的基础上加入白噪声ω[11]

(12)

假设白噪声ωi满足N(μi,εi)的正态分布，对式(12)标准化处理，得

(13)

(14)

对式(14)联合概率函数取对数可得似然函数，如式(15)所示

(15)

式中：μi为噪声均值；εi为噪声方差；L为测量段长度，m，即传感器1和4之间的距离。

上式中，Ki，σ1α1和σ2α2可通过去噪后的纯泄漏信号进行幅值计算，μi和εi由噪声信号获得，将实验信号所得到的数值代入式(15)，使用MLE即可对该公式进行求解，求得x1。

2 实验设备与操作

由于测量油品泄漏会有较大危险性，所以本文采用水代替油品进行实验。

实验装置包括管道系统和数据采集系统，如图3。该水管由法兰连接，法兰连接处有橡胶垫圈，管长67 m，阀门安装在距离上游水流入口33.5 m的地方。管道外径108 mm，壁厚3 mm。运行时压力0.1 MPa，流量为32～34 m3/h。管线为碳钢材质，焊缝宽度为5.3 mm，焊缝系数为0.85。

图3 水管泄漏声波检测与定位装置

阀门开启时假定为泄漏状态，为了探讨不同泄漏口径下，本文所用定位方法的准确性，设置了不同大小的泄漏孔；泄漏孔的直径分别为3,6,8,10,12,15,20和27 mm。不同的测量距离会影响传感器接收到的信号强度，测量距离越远，信号越弱，也就影响了泄漏定位的精度。因此，本研究通过控制变量，在相同的泄漏尺寸下设置了不同的测量距离。

由于声发射泄漏检测是一种无损检测方法，所以传感器可以沿着外壁管道的任意位置固定，以捕获声压信号[12]。本实验进行了两组不同距离的测量，分别对应图1传感器1,2,3,4的不同位置，实验中传感器位置设置如表1，表中距离为传感器到泄漏口的距离。

表1 传感器位置布置表

实验设备如图3，在PCI-2系统中，R15a谐振传感器非侵入性地获得包含噪声的泄漏信号，该传感器采样率范围为1～3 000 kHz；利用40 dB的前置放大器放大微弱的输入信号；18位a/D转换的声发射处理卡，即PCI-2采集卡进行数据处理；数据在AEwin软件中显示。在阀门开启，管道内液体流动稳定之后以200 kHz的采样频率进行数据采集，每次采集持续时间为25 s，每组工况采集3次数据。

3 实验结果

3.1 数据处理

由数据采集系统直接获得的原始AE信号如图4所示。上述实验获得的信号，首先用VMD(variational mode decomposition)方法将噪声信号从实验获得的信号中分离出来，以便获得噪声参数；原始信号去除噪声信号后被认定为纯泄漏信号，纯泄漏信号被用于计算式(8)、式(10)和式(12)中的幅值。

图4 数据采集系统所得的原始AE信号图

VMD在运行前，需要预设二次惩罚项ξ，分解模态分量个数k，噪声容忍度τ以及收敛准则容差值φ，根据相关计算结果，最终预设值如表2所示。

表2 VMD相关运行参数设置

分解出的7个模态分别标记为u1～u7。随机选取实验获得的声发射信号作为VMD输入信号，得到原始信号及VMD分解之后的各模态频谱图如图5所示，各模态有其各自的中心频率。计算各模态与原始信号之间的相关系数，将相关系数大于0.3的模态进行重构[13]。经过计算，u2～u7与原始信号之间相关系数大于0.3，即对u2～u7重构，记为去噪之后的信号；u1被设定为噪声信号。

图5 原始信号频谱与VMD分解后各模态频谱图

分离出的噪声信号与纯泄漏信号需要白化[14]。白化后的噪声信号用于计算噪声方差与均值。白化后的纯泄漏信号经过特征值提取，首先得到能量值，幅值则用能量的开方获得。能量值计算公式为

(16)

式中:xi为重构信号;M为每个信号中采样点数。实验设定采样时间为25 s，但是实际操作时，采样的时间会由于操作人员的反应速度以及软件反应速度等因素产生微小差异。考虑到不同泄漏口径进行实验时，采样时间的微小差异会影响能量计算结果，进而影响幅值结果，因此在原有能量值的基础上，将按照采样时间与能量值的比例，计算5 s采样时间的能量值。第一组传感器布置距离在不同泄漏尺寸下声波信号幅值计算结果在表3中显示(三次实验的平均值)；第二组距离在表4中显示(三次实验的平均值)。将表3和4的数据画图6和图7，以求更直观地分析数据。

表3 第一组距离布设下不同泄漏尺寸声波信号幅值表

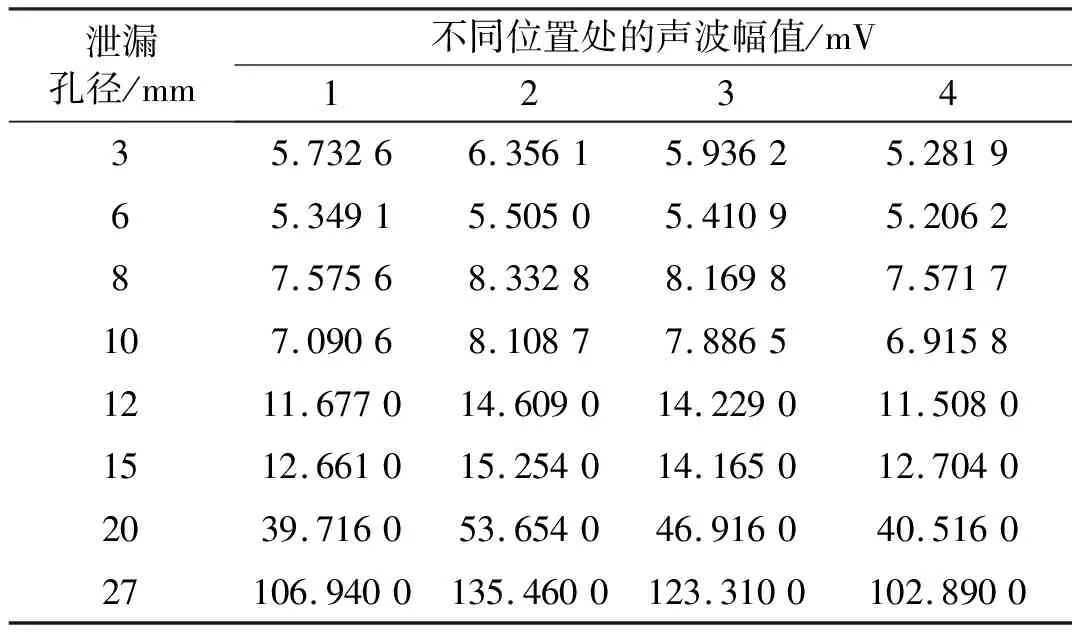
表4 第二组距离布设下不同泄漏尺寸声波信号幅值表

图6 第一组传感器布设下不同泄漏口径幅值对比图

图7 第二组传感器布设下不同泄漏口径幅值对比图

图6中，3,6,8,10,12和15 mm之间幅值差异较小，原因在于泄漏尺寸之间差距较小；而20 mm和27 mm之间幅值差异就比较明显。随着泄漏口径的增加，幅值逐渐增大，12 mm的幅值除外，原因推断是，在该条件下当泄漏孔小到一个临界值时，由于出现管路膨胀振动形式[15]，增强了传感器接收到的声发射信号。

图7中，3 mm的信号幅值大于6 mm；8 mm的信号幅值大于10 mm；与第一组距离的规律不同。由于声波沿管道传播过程中不同的频率衰减程度是不同的，也就意味着不同探测距离，传感器所探测到的信号中占主导的频率是不同的。在第二组距离中，3 mm信号幅值大于6 mm的原因推断是3 mm泄漏口处液体汽化，从而发生气固耦合[15]，增强了AE信号中的某一频率，而在该探测距离下，这一频率在声信号中占主导，所以造成了第二组距离的实验现象。8 mm信号幅值大于10 mm原因是8 mm管径在该探测距离下，管路发生膨胀振动形式，且对应的频率在声信号中占主导。

本文所用方法只需要确定每一组实验中不同传感器之间的信号幅值比，定位结果的准确性主要取决于幅值比值。因此，不同泄漏口径之间幅值的大小对比不影响结果。

3.2 定位结果

(17)

在两组不同测量距离下，用基于衰减模型的极大似然估计得到的定位结果如表5。由表5中三组实验数据得到的误差平均值做不同泄漏口径及不同传感器布设下定位误差对比，如图8所示。

表5 不同测量距离处泄漏定位结果

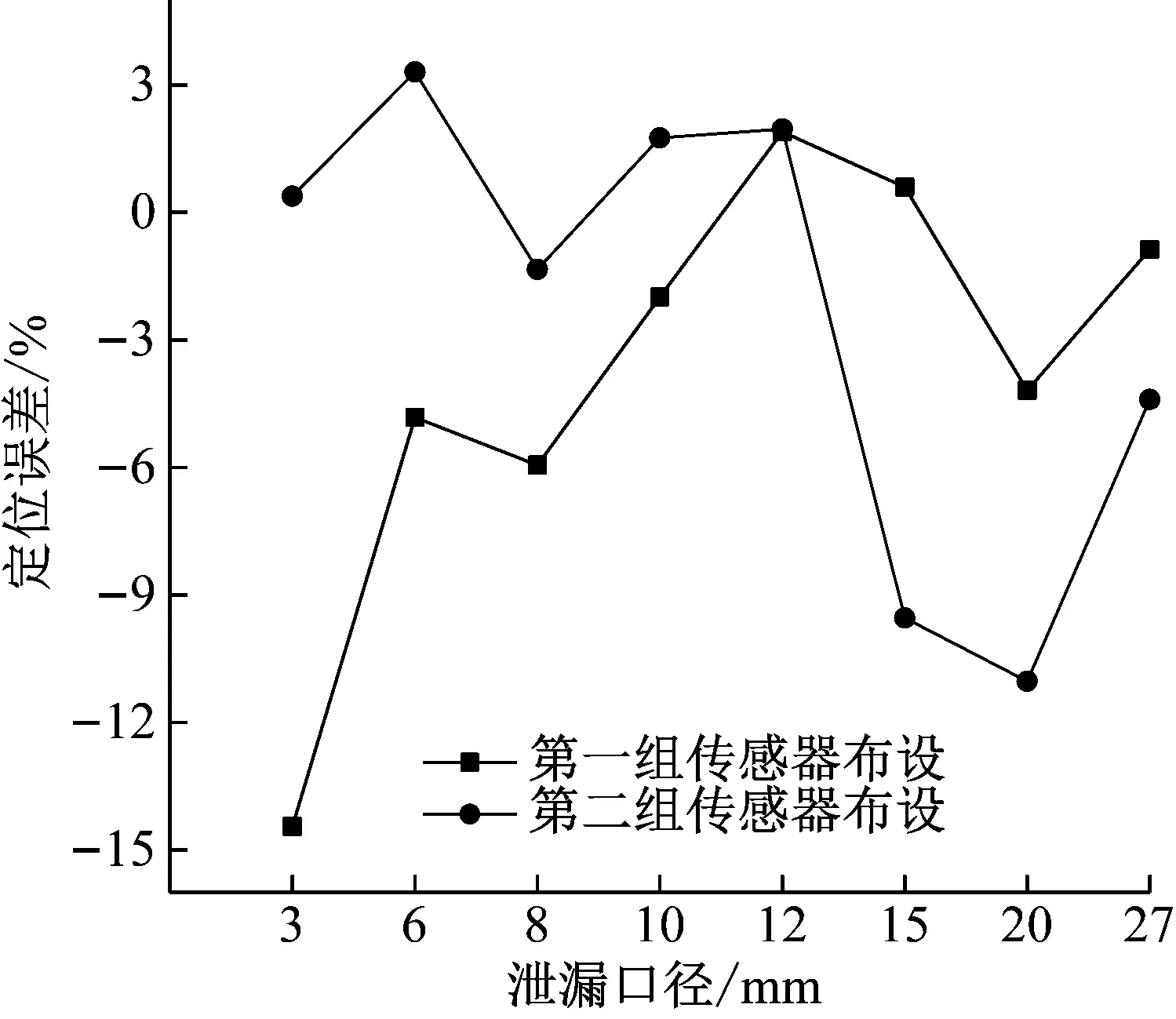
图8 不同泄漏口径及不同传感器布设下定位误差对比图

表5中可见，第一组距离，3 mm泄漏孔的实验1和实验3所得结果较差，推断是由于泄漏口径较小，导致传感器接收的泄漏信号较弱，被湮没于噪声信号中，从而影响幅值计算结果。

由图8可知，第一组传感器布设的条件下，3 mm的泄漏口径误差最大。而在第二组传感器布设的条件下，15 mm和20 mm的误差较大。除此之外，其他预测值误差都在6%以内，所有实验数据中最大的误差也不超过15%，说明该方法能较好地对泄漏点进行定位。也说明在本文的实验中，传感器的探测距离对定位结果的影响较小。

该实验的误差来源于：

(1)在测量传感器距泄漏口的距离时，由于测量工具精度以及测量方法产生的误差。

(2)当泄漏点距离焊缝、法兰等管道特征较近时，由于反射波的影响，会使定位出现较大误差[16]。

(3)传感器的采样率不够，导致测量得到的信号不能较完全地反映泄漏情况。

式中，j和l表示φ(jΔx,lΔy)所形成二维矩阵的第j行第L列，Δκx=2π/Dx和Δκx=2π/Dx分别为x方向和y方向频率间隔，Dx=NxΔx和Dy=NyΔy分别为相位屏两个方向上的长度，Nx和Ny分别为两个方向上的网格数，Δx和Δy分别为两个方向上的网格间距.

(4)在对声发射信号的处理过程中，使用的VMD去噪方法分离的噪声与纯泄漏信号，与实际的噪声和泄漏信号有所差别。

(5)极大似然估计法只能估计出最优位置，但是结果可能与实际泄漏位置之间会有误差。

为了佐证该方法的有效性，对现有设备选取一段较长直管进行试验。在管段上选取一点进行敲击，共实验三次，且每次敲击强度不同。实验中敲击点位于传感器2与3之间，传感器与敲击点之间距离如表6所示。