基于圆锥微凸体的结合面法向刚度分形模型研究
2021-08-11兰国生谭文兵张学良温淑花陈永会
兰国生,孙 万,谭文兵,张学良,温淑花,陈永会
(太原科技大学 机械工程学院,太原 030024)
机械结构中存在着大量的结合面,结合面刚度是机械结构整体刚度的重要组成部分。结合面刚度对整机的静态特性以及动态特性有着十分重要影响[1-2]。文献[3]指出机床结合面的刚度约占机床总刚度的60%~80%,结合面引起的变形量约占机内静变形量的85%~90%。为此,许多学者对机械结合面的刚度做了大量研究。张学良等[4]建立了球面与平面接触的法向接触刚度分形模型;兰国生等[5]基于域扩展因子和改进W-M函数提出了结合面接触分形模型;王润琼等[6]考虑了微凸体相互作用建立了结合面接触刚度模型;陈永会等[7]提出了粗糙表面弹塑性接触连续光滑指数函数模型,并在此基础上研究了法向接触刚度;刘伟强等[8]构建了椭圆抛物体形微凸体曲面弹性接触模型;Adams等[9]研究了弹性圆锥与弹性半空间的接触问题;许志倩等[10]建立了基于圆锥与平面接触的三维粗糙表面接触力学模型;田洪亮等[11]将圆锥微凸体应用在粗糙表面接触分析中,建立了结合面法向刚度统计模型,该模型中的粗糙表面统计参数受取样长度和测试仪器的分辨率的影响,不具有客观唯一确定性。
以上研究工作大多基于球体与平面接触的模型,研究粗糙表面接触力学特性。然而结合面上微凸体理想化的模型与实际差别还是很大的,实际微凸体各自大小和形状都不一样,因此结合面上存在球形、椭球形、抛物体、圆锥体等各种形状的微凸体,采用圆锥模拟微凸体可以为结合面进一步的研究提供基础。因此,本文以圆锥体等效粗糙表面上的微凸体,并结合分形理论和改进的W-M函数,建立了结合面法向接触刚度分形模型,并通过仿真分析了相关因素对结合面法向接触刚度的影响。最后将本文模型与经典模型以及文献[12]中试验数据进行比较,验证了本文模型的准确性。
1 粗糙表面的圆锥微凸体模型
1.1 粗糙表面建模
文献[13]提出了可以更好模拟粗糙表面轮廓的改进W-M函数,微凸体的变形量δ可由其余弦函数的波峰和波谷的幅值表示,即
(1)
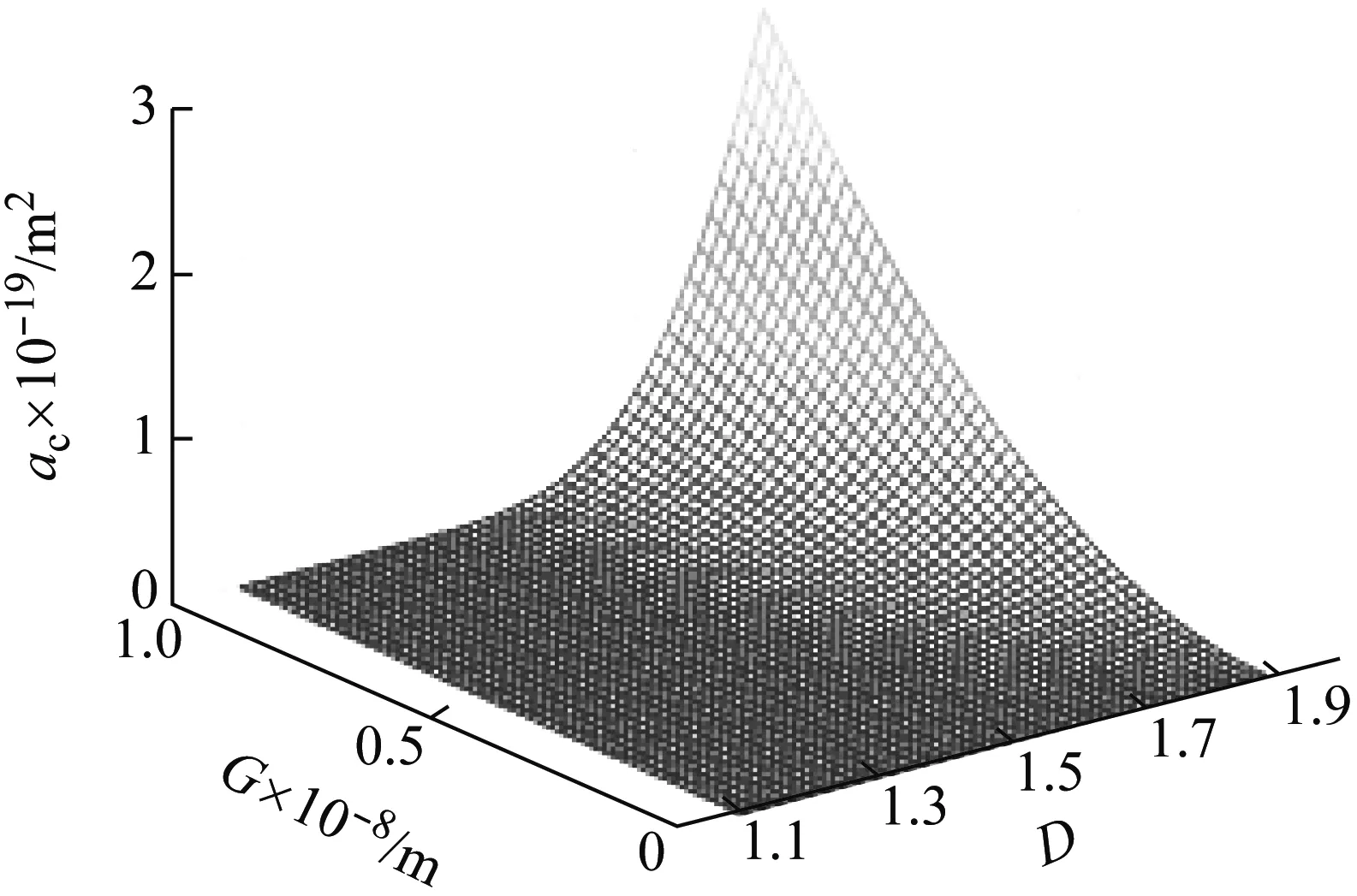
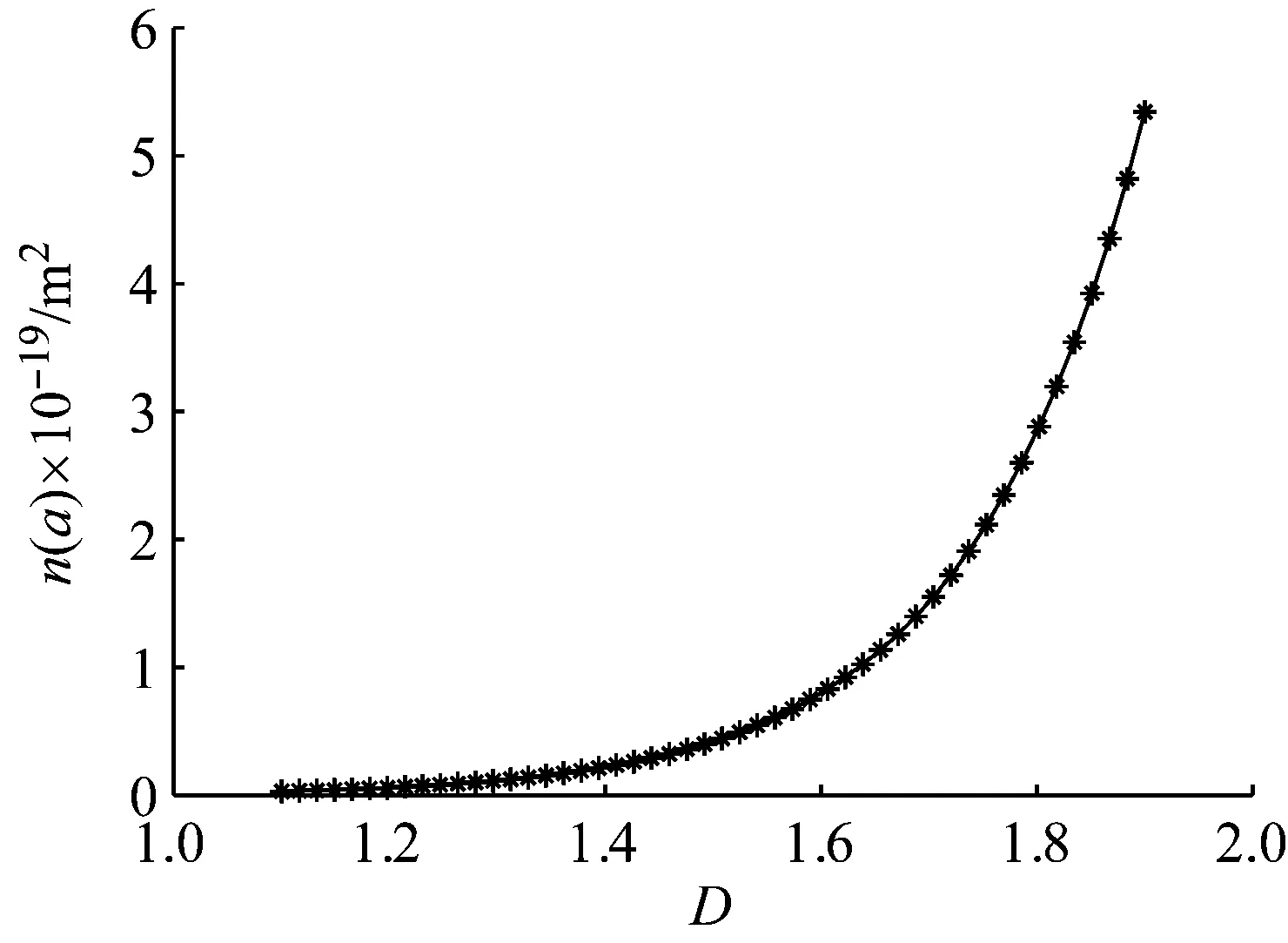
式中:G为分形粗糙度参数;D为粗糙表面分形维数(1 相互接触的粗糙表面可以简化为一粗糙表面和一刚性平面相互接触,一般粗糙表面上的微凸体可以等效为球形、柱形、锥形,球形模型比较常用,柱形模型与实际接触情况不符,锥形比较接近实际[14],因此本文用圆锥模拟粗糙表面上的微凸体。单个圆锥微凸体的变形量为δ,接触半径为r,半顶角为β,如图1所示。 图1 微凸体等效模型 如图1所示,球形模型等效微凸体时,以余弦波曲率半径为球形半径。根据文献[15]可知,由余弦波包裹微凸体,对应的微凸体中有空白致使等效微凸体的体积大于真实体积,为此本文与等效球形方法类似并适当减小余弦波所包裹的体积,以余弦波顶点和余弦波与刚性平面接触的边界两点作等腰三角形(即为等效圆锥体的正视图),则圆锥微凸体的半顶角余切值可以表示为 (2) 式中,a为微凸体接触面积a=πr2。 根据式(2)并取a=10-15m2,G=10-15~10-8m,D=1.1~1.9进行仿真,仿真结果如图2所示。 图2 D和G对cot(β)的影响(a=10-15 m2) 由图2可得,圆锥微凸体的半顶角余切值随着分形维数的增大而减小,随着分形粗糙度参数的增大而增大。进而可知,对于相同接触面积的不同微凸体,分形维数越小,分形粗糙度参数越大,微凸体越“扁平”;分形维数越大,分形粗糙度参数越小,微凸体越“尖锐”。 由图1可得,圆锥微凸体变形量和接触面积之间的关系为 (3) 由文献[16]可得,圆锥微凸体在弹性阶段所受载荷和接触面积的关系为 (4) 式中:E为两接触材料的综合弹性模量;E1和E2分别为两接触材料的弹性模量;υ1和υ2分别为两接触材料的泊松比。 由式(4)可得,圆锥微凸体在弹性阶段所受的平均压强为 pea=0.2Ecot(β) (5) 将式(2)代入式(4)可结合分形参数D,G,即 (6) 根据刚度的定义,单个圆锥微凸体的法向刚度可以表示为 (7) 将式(3)和式(4)求导后代入式(7)可得 (8) 当圆锥微凸体发生塑性变形时所受总载荷为 pp=Ha (9) 式中,H为两接触材料中较软材料的硬度。 由式(9)可得,圆锥微凸体在塑性阶段所受的平均压强为 (10) 圆锥微凸体由弹性状态进入弹塑性状态时,可设施加在圆锥微凸体上的压强在临界变形量处连续,即 pea=ppa (11) 将式(5)、式(2)和式(10)代入式(11)可得,结合面微凸体临界接触面积为 (12) 式中:k=H/σy;φ=σy/E;σy为相互接触材料中较软材料的屈服强度;φ为塑性指数;k一般为2.8。 根据式(12)并选取结合面参数取值φ=0.7~2.5,G=10-15~10-8m,D=1.1~1.9,k=2.8进行仿真,仿真结果如图3和图4所示。 图3 D和G对ac的影响(φ=1.5,k=2.8) 图4 φ对ac的影响(D=1.6,G=10-12 m,k=2.8) 由图3和图4可得,结合面微凸体临界接触面积随着分形维数和分形粗糙度参数的增大而增大,随着塑性指数的增大而减小。 由文献[17]可知接触面积分布密度函数表达式为 0 (13) 式中,al为所有微凸体中最大接触面积。 根据式(13)并取al=10-10m2,a=10-15m2,D=1.1~1.9进行仿真,仿真结果如图5所示。 图5 D对n(a)的影响(al=10-10 m2,a=10-15 m2) 由图5可得,结合面接触面积分布密度随着分形维数的增大而增大。进而可知,对于结合面相同实际接触面积区域内,分形维数越大,发生接触变形的微凸体个数越多。 结合面上的实际接触面积为 (14) 结合面的法向总载荷为 (15) 将式(6)、式(9)和式(13)代入式(15)可得 (16) 结合面的法向总刚度为 (17) 将式(8)和式(13)代入式(17)可得 (18) 将式(16)和式(18)无量纲化, (a)D=1.1 (a)D=1.1 (a)D=1.1 图和D对的影响(G*=10-10,φ=1.5) (a)D=1.1 (a)D=1.1 综上所有仿真结果进一步分析: (1)当结合面实际接触面积一定,分形维数小于1.5时,随着分形维数的增大,相同接触面积的圆锥微凸体的半顶角余切值明显减小,致使所受弹性力减小;临界接触面积增大,致使处于塑性状态微凸体(具有较小接触面积)的数量占比略微增加,同时处于弹性状态微凸体(具有较大接触面积)的数量占比略微减少;此外,结合面相同实际接触面积区域内发生接触变形的微凸体个数略微增多。前两者因素(致使结合面法向载荷相对减小)起主要作用,后一因素(致使结合面法向载荷相对增加)起次要作用,最终致使结合面法向载荷相对减小。同理,随着分形维数的减小,结合面法向载荷相对增大。 (2)当结合面实际接触面积一定,分形维数大于1.5时,随着分形维数的增大,相同接触面积的圆锥微凸体的半顶角余切值略微减小,致使所受弹性力减小;微凸体临界接触面积增大,致使处于塑性状态微凸体(具有较小接触面积)的数量占比明显增加,同时处于弹性状态微凸体(具有较大接触面积)的数量占比明显减少;此外,结合面相同实际接触面积区域内发生接触变形的微凸体个数明显增多。这与分形维数小于1.5时的情况相反,前两者因素(致使结合面法向载荷相对减小)起次要作用,后一因素(致使结合面法向载荷相对增加)起主要作用,最终致使结合面法向载荷相对增大。同理,随着分形维数的减小,结合面法向载荷相对减小。 (3)当结合面实际接触面积一定,分形粗糙度参数的增大时,相同接触面积的圆锥微凸体的半顶角余切值增大,致使所受弹性力增大;微凸体临界接触面积增大,致使处于塑性状态微凸体(具有较小接触面积)的数量占比增加,同时处于弹性状态微凸体(具有较大接触面积)的数量占比减小;此外,结合面相同实际接触面积区域内发生接触变形的微凸体个数不变。第一因素(致使结合面法向载荷相对增大)起主要作用,第二因素(致使结合面法向载荷相对减小)起次要作用,最终致使结合面法向载荷相对增大。同理,当分形粗糙度参数的减小时,结合面法向载荷相对减小。 (4)当结合面实际接触面积一定,分形维数的增大时,临界接触面积增大,致使处于弹性状态微凸体的数量占比减少;结合面相同实际接触面积区域内发生接触变形的微凸体个数略微增多。前者因素(致使结合面法向接触刚度相对减小)起次要作用,后一因素(致使结合面法向接触刚度相对增加)起主要作用,最终致使结合面法向接触刚度相对增大。同理,随着分形维数的减小,结合面法向刚度相对减小。 (5)当结合面实际接触面积一定,分形粗糙度参数的增大时,临界接触面积增大,处于弹性状态微凸体的数量占比减小;结合面相同实际接触面积区域内发生接触变形的微凸体个数不变。前者因素致使结合面法向法向接触刚度相对减小。同理,随着分形维数的减小,结合面法向刚度相对增大。 参考文献[12]和文献[19]中粗糙表面接触力学试验的基础特性参数均是通过施加一定的外载荷、动态激励等外部作用,经过传感器转化成数字信号,最后通过模拟测试确定结合面的动力学特性,同时固定结合面间的最大静压强小于3 MPa且尽量保证压力在两试件接触的结合面上均匀分布,以便保障试验数据的有效性。粗糙表面分形参数均是采用结构函数法计算获得的。参文献[12]中的试验样本材料均为铸铁,试样材料的硬度、弹性模量和泊松比分别为H=220 MPa,E1=E2=100 GPa,υ1=υ2=0.25;文献[19]中的试验样本材料均为灰铸铁,试样材料特性参数为H=231 MPa,E1=E2=130 GPa,υ1=υ2=0.25。试样表面轮廓分形参数见表1,各个试样采用不同加工方法组成不同结合面,文献[12]中结合面的名义接触面积均为Aa=10 000 mm2,文献[19]中结合面的名义接触面积均为Aa=11 200 mm2,结合面间无润滑,其等效接触表面分形参数见表2。文献[12]试验简图如图14,详细试验方法为:通过四个螺栓对结合面施加静态预紧力(可以使用扭矩扳手将负载调整到指定值),并通过冲击锤在上部件的表面上激发激振力。三轴加速度传感器固定在下部件上,用橡胶绳将试样悬挂,以防止底座的激振响应影响测试。应用了多点激励方法,并从固定的三轴加速度传感器收集了响应信号,通过模拟测试确定加工的结合面的动力学特性,其中通过将模拟结果拟合到第一和第二共振频率的试验值中来识别结合面的接触刚度。文献[19]试验简图如图15,详细试验方法为:首先将滑块安装在导轨的测试台上,并通过扭矩扳手将负载螺栓调整到一定的法向负载,将弹性橡胶垫圈安装在螺栓下方,以避免螺栓刚度对结合面刚度的影响。安装加速度传感器后,通过冲击锤将激振力施加到组装好的滑块上,同时数据采集系统将收集到的响应信号发送到CutPro软件,然后可以从软件的频率响应分析中获取FRF数据。最后可以通过一组弹簧阻尼器来模拟结合面的动态特性来确定结合面的刚度参数。根据表2顺序分别将三组试验数据记为试验数据1、试验数据2、试验数据3。本文模型是以圆锥等效粗糙表面上的微凸体,文献[12]中的模型是以球等效粗糙表面上的微凸体,记为JZZ模型。将上述参数代入本文模型和JZZ理论模型与试验数据1、2、3对比,对比结果如图15~18所示。 图14 文献[12]试验示意图 图15 文献[19]试验示意图 表1 不同试样的分形参数值 表2 接触表面的等效分形参数值 图16 不同模型与试验数据1比较 图17 不同模型与试验数据2比较 由图15~18可见,本文模型与试验数据基本吻合,证明了本文模型的正确性,相比与JZZ模型,本文模型的精确性得到了一定的提高。粗糙表面接触刚度与表面粗糙度有关,然而表面粗糙度是由加工方法产生的,因此加工方法对粗糙表面接触特性有着直接的影响。特征分形参数D和G是表面多尺度相似测量与绝对测量的统一,因而它既具有分形测量多尺度性的特点,也保留了常规粗糙度参数直观和简明的优点。本文理论模型计算值偏离试验值的主要原因在于:本文模型忽略微凸体之间的相互作用以及形变时材料强化作用;微凸体的变形方式可以分为塑性、弹塑性和弹性这三个状态,在本文中为简化问题只考虑塑性与弹性这两个状态。 图18 不同模型与试验数据3比较 (1)将粗糙表面上的微凸体等效为圆锥体,结合分形理论和改进的W-M函数,建立了结合面法向接触刚度分形模型。 (2)结合面无量纲法向接触载荷随着无量纲接触面积、无量纲分形粗糙度参数和材料塑性指数的增大而增大;随着粗糙面分形维数的增大先减小后增大,且在分形维数等于1.5附近时达到最小值。 (3)结合面无量纲法向接触刚度随着无量纲法向接触载荷和材料塑性指数的增大而增大;随着粗糙面分形维数的增大先增大后减小,且在分形维数等于1.6附近时达到最大值;随着无量纲分形粗糙度参数的增大而减小。 (4)本文模型理论预测值与试验数据趋势相同,验证了本文理论模型的准确性,可用于相关的理论分析与预测。1.2 圆锥微凸体的受力与变形



2 结合面的接触模型
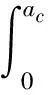
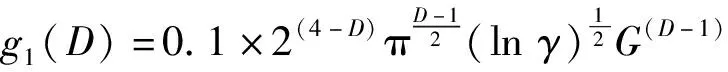


3 本文模型的数字仿真以及试验对比
3.1 仿真计算

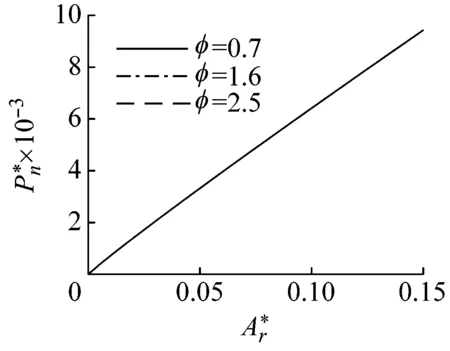
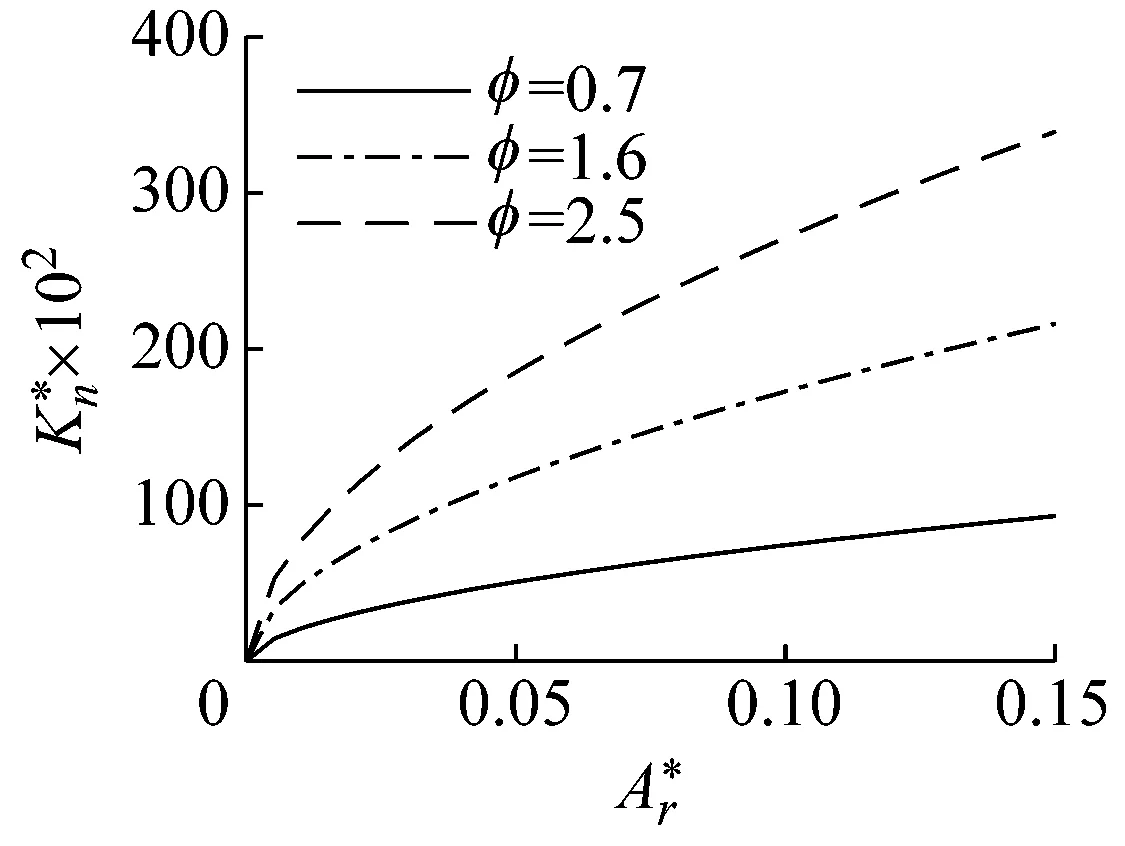
3.2 仿真结果分析

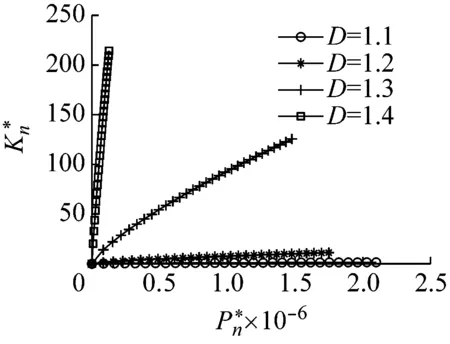




3.3 试验验证
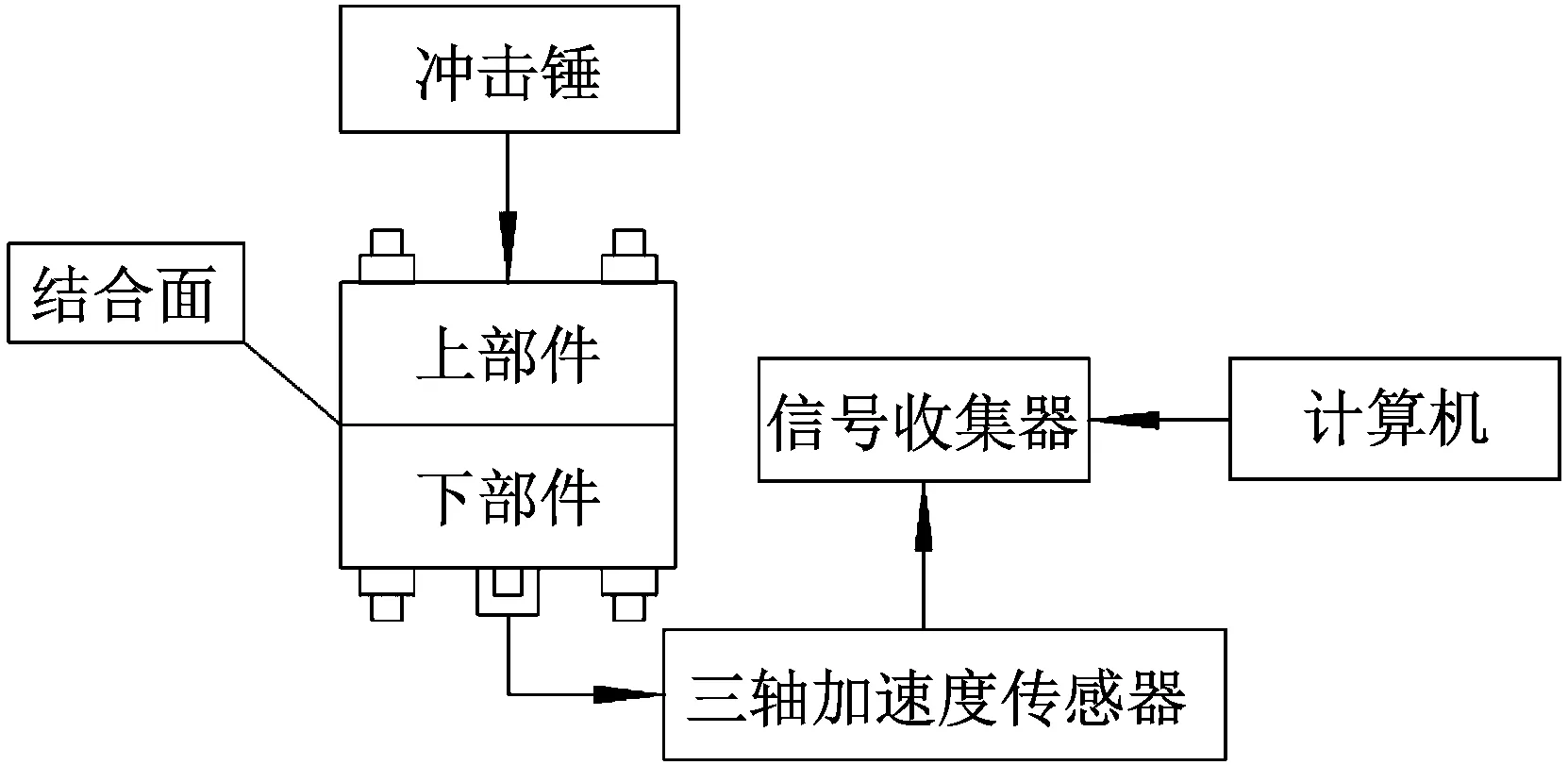



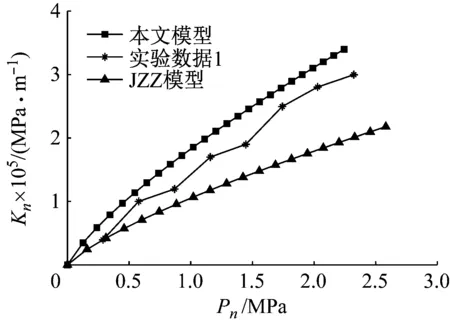
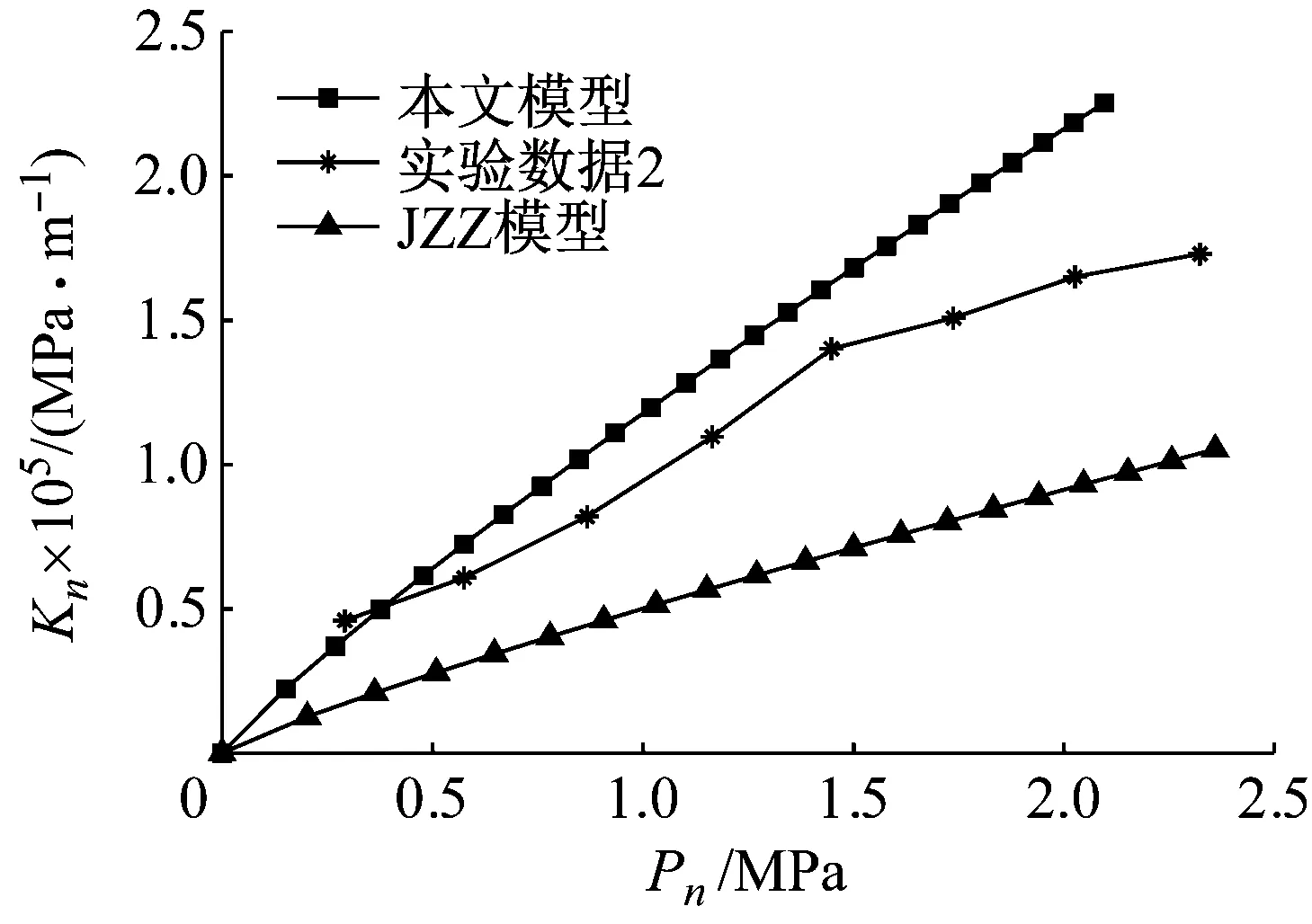

4 结 论
