不同距径比下管道后车环隙螺旋流脉动强度特性
2021-08-11刘亚坤孙西欢李永业
吴 剑,刘亚坤,孙西欢,李永业,张 帝,杨 姣
(1.大连理工大学 建设工程学部,辽宁 大连 116024;2.太原理工大学 水利科学与工程学院,太原 030024; 3.晋中学院,山西 晋中 030600)
1 研究背景
为了有效补充管道水力输送技术,克服现有管道运输体系困难,孙西欢等[1]于2007年正式提出了筒装料管道水力输送的概念。在该输运方式中,物料密封于圆柱状料筒内,被水流推动以实现空间输送。这种新的输运方式有着诸如占地面积小、地形限制少、安全性能高、几乎不受天气影响、更节省人力等优势,具有广泛的应用前景。
目前,对该技术的研究集中在管道车的运移特性和水流的水力特性方面。通过前人大量的研究,该技术有了很大进展。在一定的输运条件下,平均车速与流量的变化规律保持一致[2];管道车运移最优工况可通过直径比和雷诺数等参数判定(重度比法、平均流速法、流速分布法)[3-4];胡志毅等[5]、黄莹彬等[6]、李永业等[7-8]对管道车的影响因素(荷载、车型、导流条安放角)进行了分析,得出了管道内水流特征与管道车参数之间的关系;张雪兰等[9-10]通过试验分析了管道内壁与管道车外壁处的压力与速度分布情况,并对有限域内的复合圆柱体绕流进行了模拟,建立了柱状体强扰动范围估算模型;Yang等[11]运用COMSOL对平直管道内管道车壁面上的应力分布情况进行了数值模拟。在管道双车研究方面,吴剑等[12-13]、马成功等[14]分别对不同车间距和流量条件下环隙螺旋流的水力特性进行了试验研究;张春晋等[15-16]基于流固耦合方法对管道双车在运动时的振动问题进行了数值模拟和试验研究。
目前,筒装料管道水力输送技术对于多个管道车的研究还相对较少,本文主要对同型管道双车在不同距径比下后车环隙水流轴向、垂向和横向脉动强度特征进行了分析。该研究成果是对同心环状缝隙流理论的补充与完善,也为实际工业化过程中管道列车调度提供参考。
2 试验设计
2.1 试验系统
试验管道由多节内直径D=100 mm的有机玻璃圆管组成,并处于同一水平面内(xOy平面),离地面约1.5 m。试验时,离心泵将水从水箱下部抽出,经调整后流入平直有机管道,并最终流回水箱,经水箱内的稳流板后流入水箱下部,形成一个闭合循环回路。试验系统布置如图1所示,管道双车在管道内的状态如图2所示。图2中:l和d分别表示管道车圆柱状料筒的长度和直径;L表示管道车总长度;S表示双车净间距;D表示管道内直径。

图1 试验系统布置Fig.1 Layout of test system
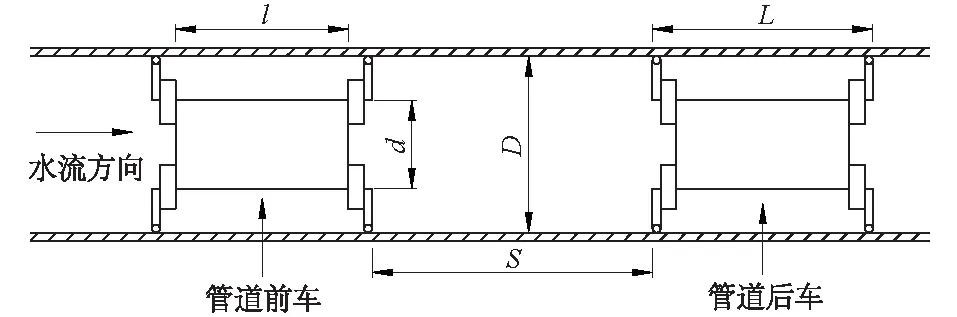
图2 管道双车示意图Fig.2 Schematic diagram of double-piped carriages
2.2 管道车
管道车由料筒、支撑体、导流条等组成。本次试验的双车型号相同,料筒长度l=150 mm,直径d=70 mm,管道车总长L=210 mm,在料筒两端面处间隔120°各安装了3个支撑体,导流条间隔120°并且错开支撑体布置。导流条长度150 mm,高度10 mm,厚度3 mm,安放角按照2°/cm的速度增长,出水端总安放角30°。管道车结构如图3所示,导流条安放角如图4所示。
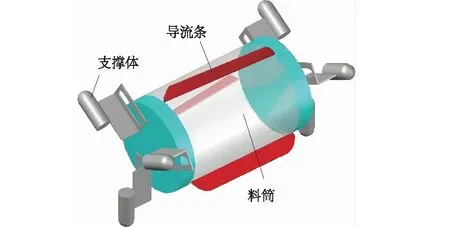
图3 管道车模型示意图Fig.3 Schematic diagram of piped carriage model
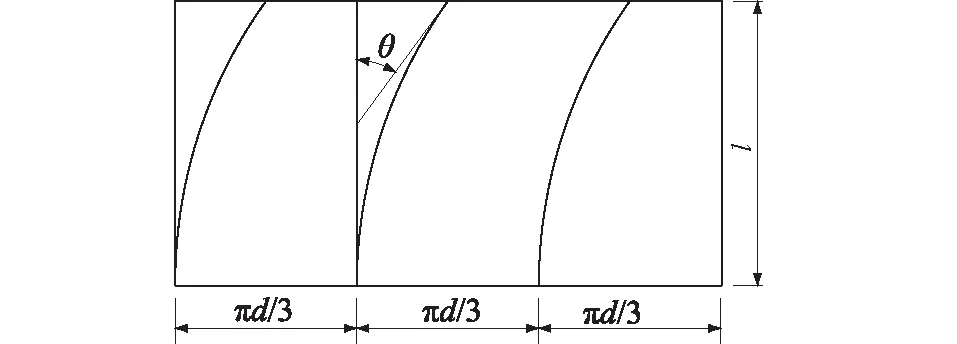
图4 导流条安放角示意图Fig.4 Schematic diagram of guide bar angle
2.3 测点布置
测试断面布设在管道车车身正中位置,按极坐标划分为12条极轴、5个测环,测环半径R1—R5分别为47、44、42.5、41、38 mm,极轴与测环的交点即为测点。测点布置如图5所示。
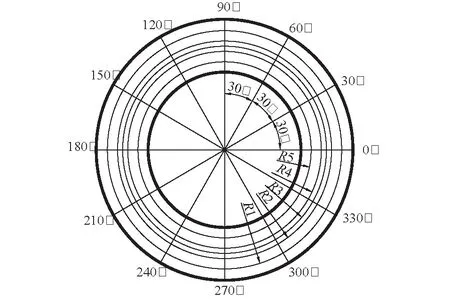
图5 测试断面测点布置Fig.5 Layout of measuring points of test section
2.4 测试工况
双车间距是本试验一个主要的控制因素,流体的水力特性和运输效率与管道车间距密切相关。本文定义距径比SD为双车间距S与管道内直径D之比(即SD=S/D),试验共选取5个间距,其SD分别为1、3、5、7、9。本次试验的流量Q=30 m3/h,管道内断面平均流速V=1.06 m/s,水的运动黏度系数ν≈8.74×10-7m2/s,雷诺数Re=1.21×105,管段内水流为湍流状态。
2.5 试验数据采集与处理
环隙内水流速度由激光多普勒流速仪(LDV)进行测定,采样频率f>200 Hz,采样时长t=15 s。试验测试段位于水槽处,定义轴向速度方向为水流方向,横向速度方向为水平面内垂直于水流方向,垂向速度方向垂直于管道平面方向,即图1中的x、y、z3个方向,同向为正,反向为负。
本文采用脉动速度的均方根来表征水流脉动强度的大小,脉动强度的相关统计参数,即算术平均值、极差、标准差、变异系数的计算公式分别见式(1)—式(4)。其中,平均值、极差、标准差的单位均为m/s,变异系数无单位。
(1)
R=umax-umin,
(2)
(3)
(4)
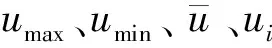
3 试验结果分析
3.1 轴向速度脉动强度
从图6来看,轴向速度脉动强度虽有所波动,但是波动不大,没有出现突增幅度较大的地方。随着SD的增加,轴向速度脉动强度的分布略有平缓的趋势,这是因为随着SD的增加,管道内水流在双车之间满管区域经过了更长距离的发展,进入管道后车的水流更加平缓一些,使得水流轴向速度脉动强度的分布也更加平缓。环隙流区内水流的轴向速度脉动强度大致呈现出“外小内大”的分布,这是由于环隙内侧的水流受到管道车的阻碍作用,水流出现绕流现象而进行一定重分布,环隙内侧水流受到的管道车影响要比外侧的大,使得内侧处的轴向速度脉动强度要高于外侧处的。
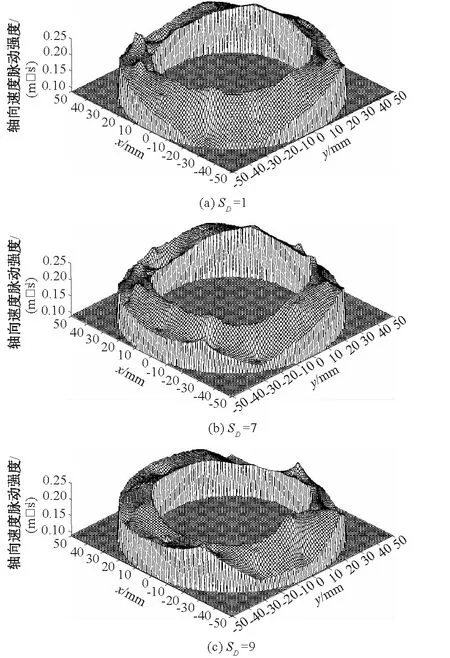
图6 不同距径比下轴向速度脉动强度分布Fig.6 Distribution of axial velocity fluctuation intensity under different SD values
从图7(a)可以看出:随着SD的增加,测试断面内轴向速度脉动强度大小在各个区间的比重变化不大,[0.2,0.23) m/s区间所占比重最大(36%),[0.17,0.2) m/s区间次之(27%),≥0.23 m/s的比重最小(2%)。从图7(b)可以看出:平均值¯u和极差R相对比较稳定,分别维持在0.18、0.14 m/s左右。随着SD的增加,轴向速度脉动强度的标准差σ和变异系数η都呈现减小的变化规律,其中,σ从0.044 m/s减小到了0.035 m/s,减小了21%;η从0.23减小到了0.19,减小了17%。这是由于随着SD的增加,管道前车对进入后车环隙区域水流的扰动影响逐渐减小。
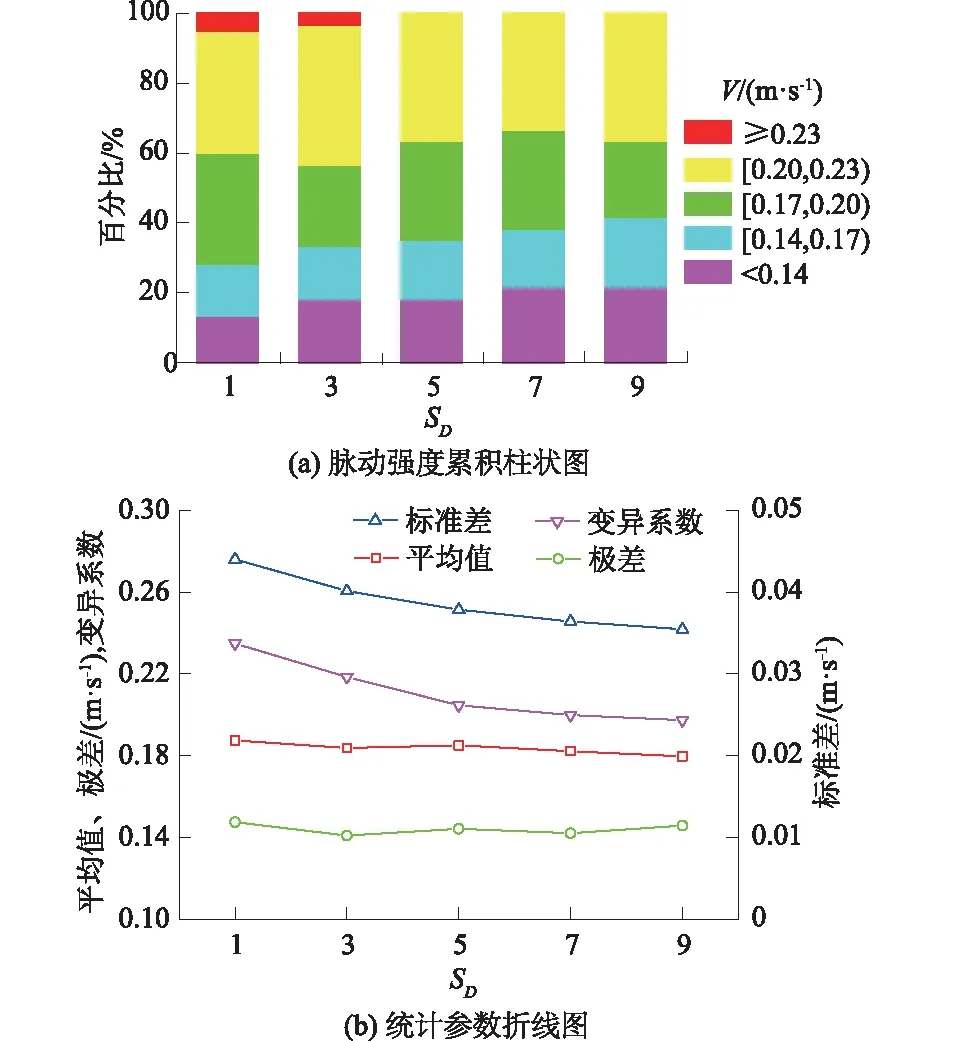
图7 不同距径比下轴向速度脉动强度统计特征Fig.7 Statistical characteristics of axial velocity fluctuation intensity under different SD values
3.2 垂向速度脉动强度
从图8来看,环隙内水流的垂向速度脉动强度在局部位置有突增,其幅度大于轴向速度脉动强度,这是由于环隙水流经过支撑体结构的扰流作用之后,在垂向方向上发展的时候受到导流条的阻碍作用,后车环隙区域的垂向速度脉动强度在局部突然增大。垂向速度脉动强度为0.012 m/s左右,垂向速度脉动强度要比轴向的小1个数量级。水流在管道中的流动主要表现为轴向流动,而垂向运动强度要小于轴向的,其脉动强度比轴向的要小。
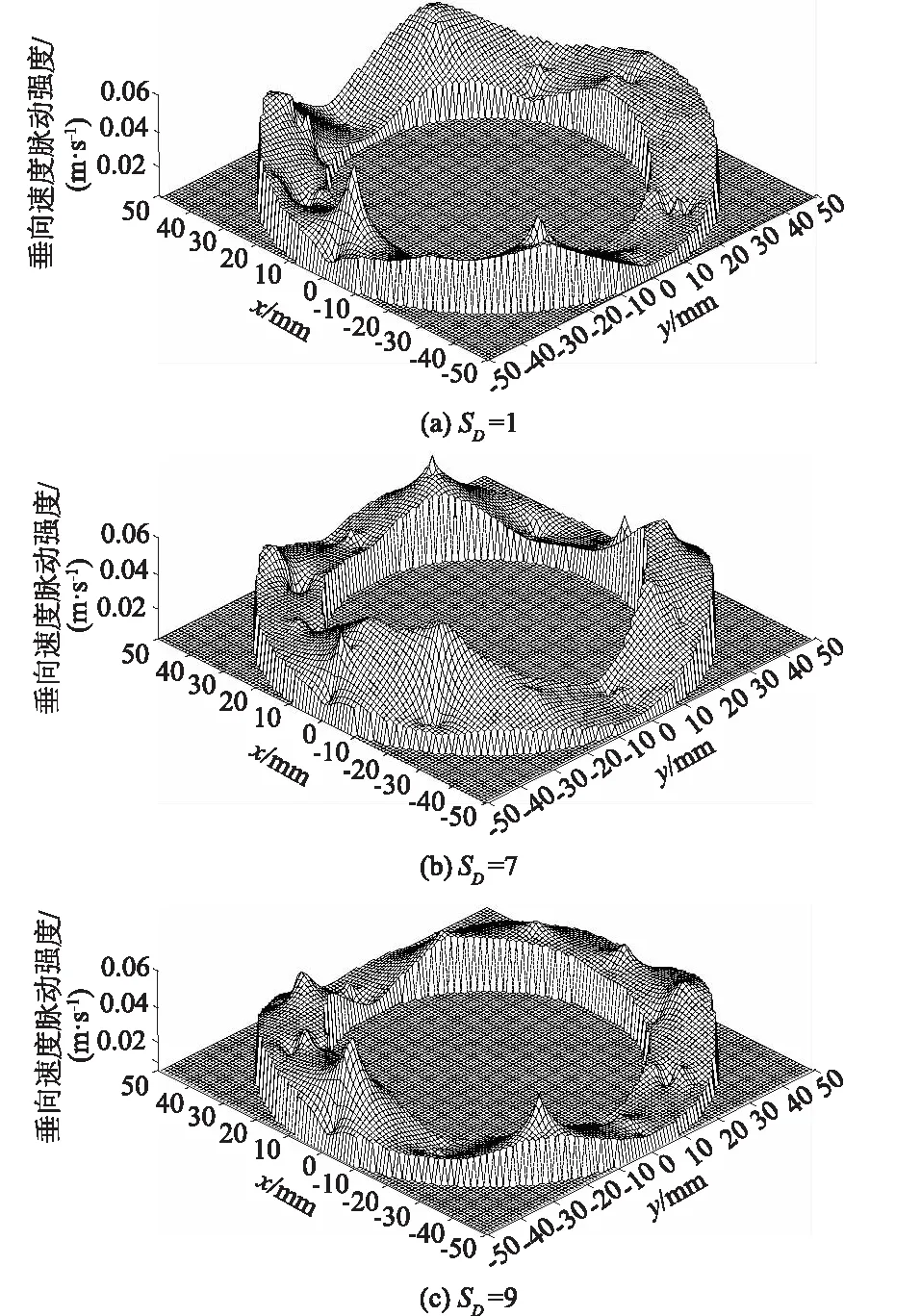
图8 不同距径比下垂向速度脉动强度分布Fig.8 Distribution of vertical velocity fluctuation intensity under different SD values
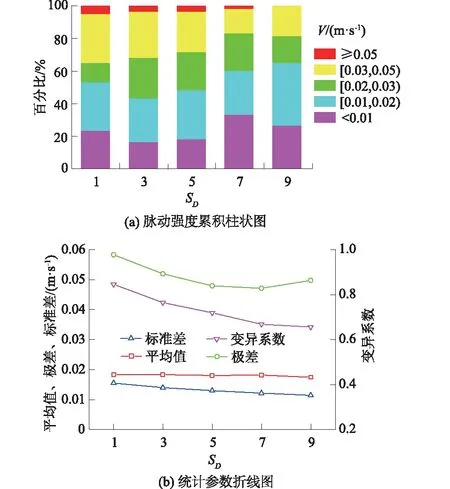
图9 不同距径比下垂向速度脉动强度统计特征Fig.9 Statistical characteristics of vertical velocity fluctuation intensity under different SD values
由图9可知,随着SD的增加,垂向速度脉动强度的标准差σ和变异系数η呈现逐渐减小的变化规律,σ从0.015 m/s减小到了0.011 m/s,减幅达27%,η从0.85减小到了0.64,减幅达25%。随着SD的增加,表征水流脉动离散程度的2个统计量都逐渐减小,说明随着SD的增加,环隙垂向水流的均匀程度逐渐增加。垂向速度脉动强度的η大约是轴向的3倍,表明垂向速度脉动强度虽然比轴向的要小,但是其离散程度比横向的要大。
3.3 横向速度脉动强度
从图10来看,横向和垂向速度脉动强度分布非常类似,其在局部位置也有突增,增加的幅值与垂向速度脉动强度突增的幅值为同一个量级,且都要小于轴向脉动速度强度的幅值。随着SD的增加,三维速度脉动强度离散程度均有所降低,脉动强度出现突增的位置和大小可能与管道车两端面处的支撑体结构有关,值得进一步研究。
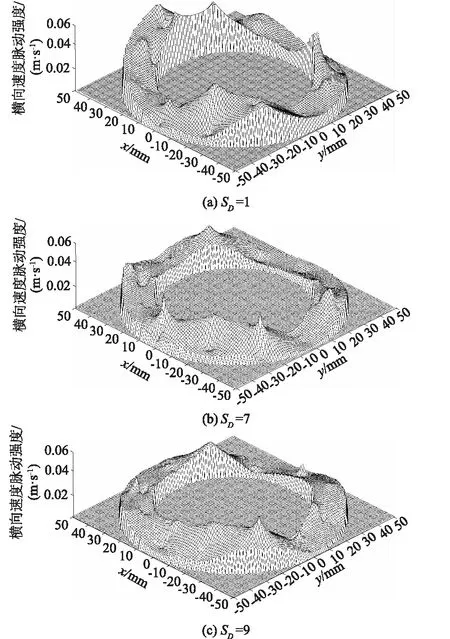
图10 不同距径比下横向速度脉动强度分布Fig.10 Distribution of lateral velocity fluctuation intensity under different SD values

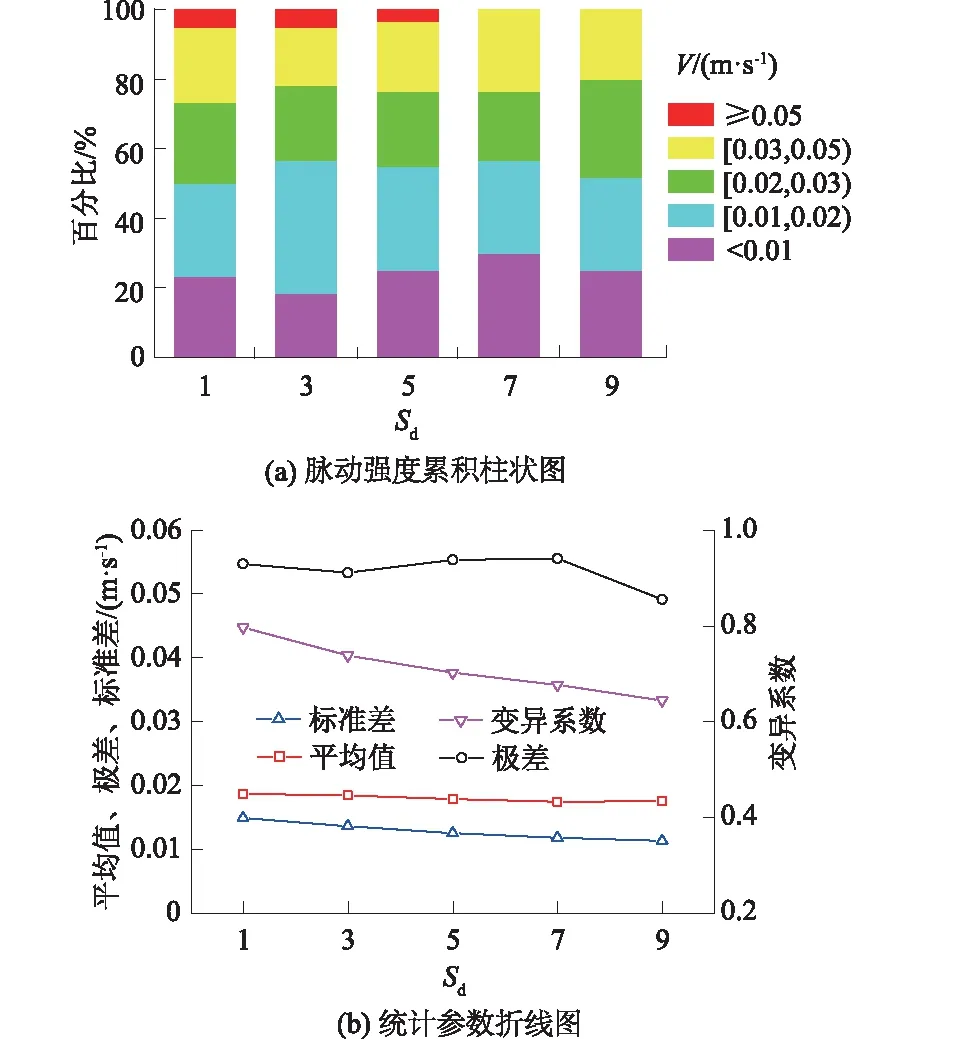
图11 不同距径比下横向速度脉动强度统计特征Fig.11 Statistical characteristics of lateral velocity fluctuation intensity under different SD values
与垂向速度脉动强度类似,随着SD的增加,横向速度脉动强度的标准差σ和变异系数η也呈现逐渐减小的变化规律,且表征离散程度的各统计特征量与垂向速度的也基本相同。σ从0.015 m/s减小到了0.011 m/s,减幅达26%;η从0.80减小到了0.62,减幅达22%。这些均表明环隙内水流垂向与横向速度脉动强度特征基本一致。
3.4 较优距径比
筒装料管道水力输送过程中,管道车之间的车间距是一个至关重要的参数。间距太小,管道前车对管道内的水流扰动剧烈,导致管道后车可能出现俯仰运动,影响运行安全;间距太大,则物料运输效率不高,经济上不划算。

表1 不同距径比下σ、η下降百分比Table 1 Decrease percentages of σ and η under different SD values
从表1可知:随着SD的增加,参数σ和η的下降基本呈现“先快后慢”的变化规律。不论何种SD下,轴向、垂向和横向速度脉动强度的σ和η下降百分比均<10%。当SD>5时,轴向速度脉动强度的σ和η下降百分比都<5%;当SD>7时,垂向和横向速度脉动强度的σ和η的下降百分比均<5%。虽然继续增大SD能一定程度地减小水流的离散程度,但减小的幅度十分有限。兼顾运行安全和输送效率,管道双车较优的SD为5~7左右。
4 结 论
(1)管道双车运行的较优SD值为5~7。
(2)轴向速度脉动强度虽有波动,但幅度不大,随着SD的增加,¯u和R基本保持稳定,σ和η都呈现减小的变化规律。
(3)垂向速度脉动强度与横向速度脉动强度的各统计特征量基本保持一致,垂向与横向速度脉动强度特征相似。
(4)无论何种SD值,垂向和横向速度脉动强度都比轴向脉动强度小1个量级,但其η值约为轴向的3倍。
(5)随着SD的增加,垂向和横向速度脉动强度的σ和η呈现逐渐减小的变化规律。
