基于正交试验法的埋地钢管参数敏感性分析

伍鹤皋，于金弘，石长征，石雅竹

(武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072)

1 研究背景

国内长距离输水工程中埋地钢管的应用逐渐增多，钢管结构的安全性及经济性问题越来越突出。埋地钢管可认为一种由钢管和土体组成的联合承载体，管周土体参数的改变通常会影响钢管的结构承载性能[1]。在埋地钢管的结构设计中，当钢管的管径和埋深确定后，回填土体的土质及压实度、垫层包角、沟槽底部开挖宽度及倾角等众多因素都将影响钢管的变形及应力状态[2]。因此，区分哪些参数对钢管结构性能影响较为显著，从而选取合适的参数，提高埋地钢管的安全性及经济性，是当前亟待解决的问题。

国内外关于埋地钢管相关参数的敏感性研究相对较少，并且通常采用单因素分析法即分析时仅变化一个参数并假定其余参数不变，来比较指标值随参数的变化关系[3]。Kawabata[4]对大直径埋地钢管回填不同材料进行对比试验，发现回填材料会显著影响钢管结构性能；Masada[5]采用解析法分别对土体模量、钢管刚度和垫层包角等参数进行研究；周正峰等[6]采用有限单元法分别对基床包角、基础刚度和管土相对刚度等参数对钢管结构的影响展开研究；Dezfooli等[7]采用有限单元法对管土间摩擦系数进行敏感性分析，结果显示该摩擦系数对钢管变形的影响较小；肖俊等[8]采用基于Spangler理论的有限单元法，通过控制土体模量来模拟因地基差异引起的柔性管道沉降问题；Card等[9]根据前人研究成果及工程经验，建议沟槽开挖宽度不超过2倍管径。

单因素分析法虽然能够比较直观地反映各参数对指标值的影响，但当考虑因素较多时，如果要对各种因素进行完全实验，将十分困难[3]。为此，本文引入正交试验法，进行大直径埋地钢管的回填土变形模量E1、砂垫层变形模量E2、垫层包角θ、沟槽底部开挖宽度B和沟槽侧壁倾角α等参数关于钢管变形和应力的敏感性分析，以区分各参数的影响大小，从而指导埋地钢管的结构设计。

2 正交试验法简介

正交试验法是采用正交表安排多因子的试验设计和分析的方法[10]。它能够大大减少试验次数而不影响拟考虑因素的性能指标，并且可以得到代表全部试验的试验数据。实际工程常常需要考虑众多因素，对各种因素进行完全试验，难以实现，例如：5因素4水平的试验，若每个因素和水平上只做1次试验，则试验次数达45=1 024次。正交试验法能够根本上解决因素多和水平多的试验。正交试验法的一般步骤见图1，其中“指标”为需要考察处理的目标，“因素”为指标的影响因子，“水平”为因素的取值[11-12]。

图1 正交试验法的一般步骤Fig.1 General steps of orthogonal test method

2.1 正交表

正交表通常记作LN(mk)，正交表中的各个元素构成了一个N行k列的矩阵，其中N、k、m分别为试验次数、因素数和水平数，例如：L8(27)正交表，它可以构成8行7列的矩阵，因素数与水平数分别为7和2，共需进行8次试验，如表1所示。正交表具有任一列中不同的水平出现的次数相同和任意两列同一行的水平数对出现的次数相同的特点，这使得试验数据具有综合可比性,以及平方和分解简单易行，能够极大地方便统计工作[10]。

表1 正交表L8(27)Table 1 Orthogonal table L8(27)

2.2 分析方法

按照正交表设计的试验方案得出各试验的指标值后，通常采用极差分析法和方差分析法来判断各因素对指标影响的敏感性大小。

2.2.1 极差分析法

极差分析法通过计算极差Rj的大小来判断因素的敏感性程度。Rj的大小反映了第j列因素水平波动下的试验指标变化情况，通常Rj越大，说明该因素对试验指标影响越显著。该方法简单易懂，可以直观地反映各因素的敏感性的高低，但无法区分试验结果的波动是由因素水平变化还是由试验误差导致的，且没有明确的界限标准判定该因素是否敏感。假定正交表为LN(mk)，极差分析过程如下。

(1) 计算出Kij，其为第j列上第i个水平的试验结果总和。

(1)

式中r为第j列上水平号i出现的次数。

(3) 计算出第j列的极差Rj，即

(2)

(4) 根据Rj分析判断因素的敏感性程度，选择最优试验方案，以及绘出因素-指标图等。

2.2.2 方差分析法

方差分析法可以估算出试验误差的大小，并给出各因素对试验指标影响程度的量化结果。为区分因素水平变化和试验误差的影响，明确各因素的敏感性程度，并验证极差分析的结果。本文同时采用方差分析法对试验结果作进一步分析。

假定正交表为LN(mk)，当试验完成后可测得N个数据，依次记为y1，y2,…，yN，数据的和记为T，即T=y1+y2+…+yN,每个水平重复数记为r=N/m。方差分析过程如下[10]。

(1) 计算出各列的水平和。每列有m个水平，水平和分别记为L1，L2，…，Lm。

(2) 计算出各列的平方和Sj及自由度fj，即：

(3)

fj=m-1，j=1,2,…,k。

(4)

(3) 计算出总平方和ST和总自由度fT，即：

(5)

fT=N-1 。

(6)

ST=S1+S2+…+Sk;

(7)

fT=f1+f2+…fk。

(8)

(4) 确定出误差平方和Se及误差自由度fe。Se由空白列的平方和与一些相对较小的列平方和之和组成，但是当无空白列且无重复试验时，可以在平方和中寻找相对较小的平方和作误差用；fe是相应列自由度之和。

(5) 进行方差分析，把上述计算出的结果写入方差分析表，然后计算均方和Vj及F比，如表2所示，其中Ve为误差平方和Se与误差自由度fe之比。在给定的检验水平α下确定拒绝域，见式(9)，并进行显著性分析。

W={F>F1-α(fj,fe)} 。

(9)

式中F1-α(fj,fe)是F分布F(fj,fe)的1-α分位数。

表2 方差分析表Table 2 Analysis of variance

3 计算模型及正交试验

3.1 计算模型

采用有限元软件ANSYS建立埋地钢管计算模型，如图2所示。x轴和y轴位于铅直面内，z轴沿管轴线方向，钢管内径3 m、管顶覆土2 m，管底垫层包角为θ，厚0.3 m，沟槽底部开挖宽度为B，沟槽侧壁倾角为α，模型宽为7B、高21.2 m，本文仅研究管道横断面问题，模型轴向长度取值对结果基本无影响，轴长取2 m即可。钢管采用Q235钢材，管壁厚14 mm，弹性模量为2.06×105MPa，泊松比为0.3，密度7 850 kg/m3，土体的材料参数列于表3，计算时不考虑天然地基的质量。钢管采用4节点壳单元Shell181模拟，土体采用8节点实体单元Solid45模拟。模型底部、前后及左右端面施加沿法向的位移约束，顶面自由，分析时考虑的外荷载主要是覆土压力。

图2 有限元模型示意图Fig. 2 Schematic diagram of the finite element model

表3 土体的材料参数Table 3 Material parameters of the soil

假定模型中的土体均遵守Drucker-Prager屈服准则。该准则在主应力空间的屈服面为光滑圆锥，在π平面上为圆形，并且考虑了中主应力和屈服引起的体积膨胀对土体的影响，数值计算效率高[13]。模型中的钢管与土体、沟槽内的土体与天然地基之间均设置面-面接触单元，并采用库伦摩擦模型模拟接触面间的相互关系。面-面接触单元依赖单元表面建立接触对，并采用穿透节点周边节点的方式来参与接触应力的计算，从而消减局部应力集中与接触压力的不均匀性，而库伦摩擦模型则是判断发生接触的两个面是否发生相对滑动的依据[14-15]。模型中管土间摩擦系数取0.25，沟槽内的土体与天然地基间的摩擦系数取0.577(tan30°)[2,16]。

3.2 设计方案及结果

根据规范及工程经验，选取回填土变形模量E1、砂垫层变形模量E2、垫层包角θ、沟槽底部开挖宽度B以及沟槽侧壁倾角α共5个试验因素，各因素均取4种水平，详见表4[2]。

表4 正交试验的因素及水平Table 4 Factors and levels in the orthogonal test

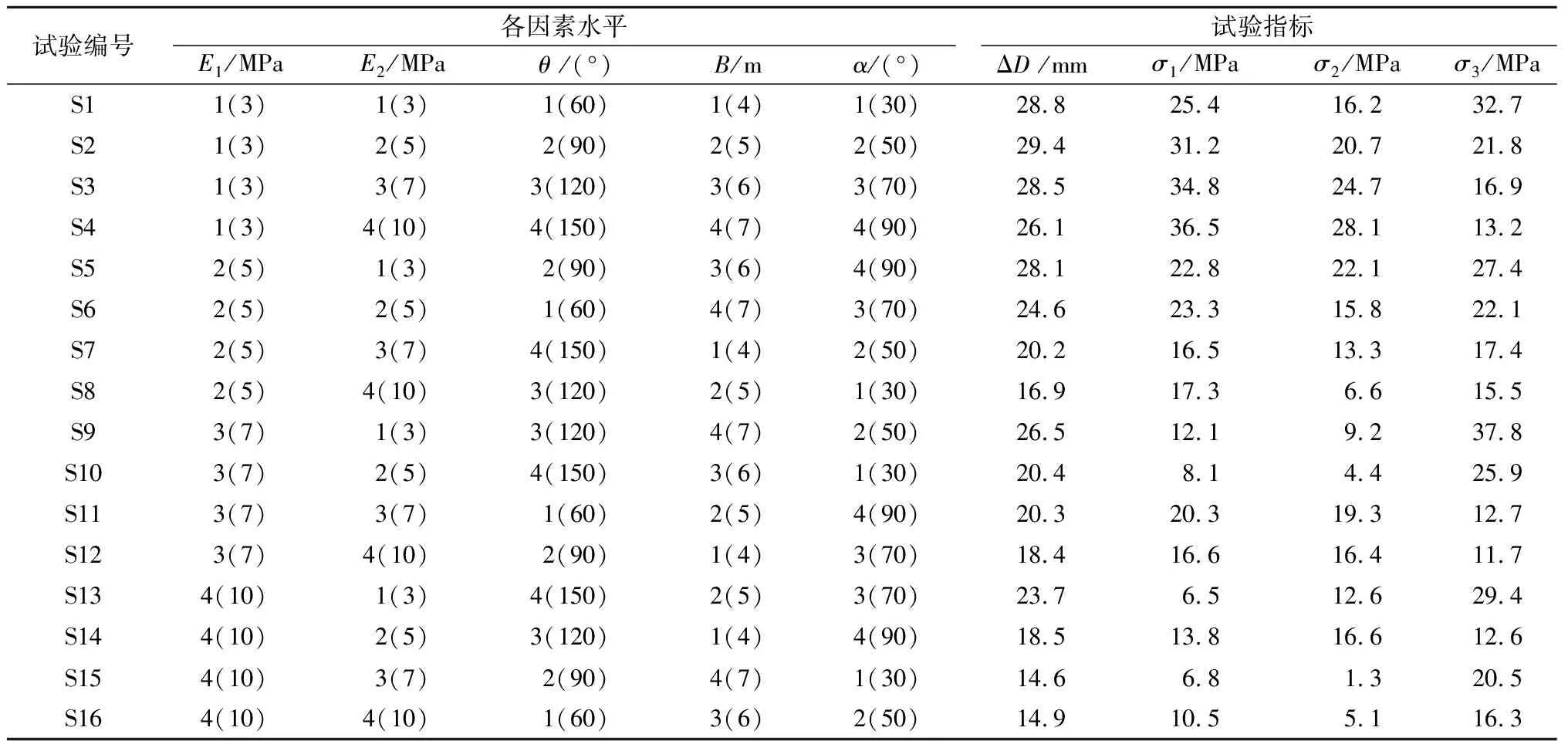
表5 正交试验设计方案及结果Table 5 Design schemes and results of the orthogonal test

由于埋地钢管设计时对θ、B、α的取值一般根据工程经验及地形地质等因素确定，较少考虑其对钢管结构的影响，且在施工时，土体变形模量较难精确控制，存在一定的不确定性。故选取上述5个因素进行研究，各因素水平取值的依据如下所述。

(1) 变形模量E和垫层包角θ的取值主要是根据《给水排水工程埋地钢管管道结构设计规程》(CECS 141:2002)。该规范对于变形模量E的取值规定为1～20 MPa；对于垫层包角θ的取值为20°～150°。实际工程中变形模量多取值在3～10 MPa，垫层包角多取值在60°～150°。为更好地指导工程实践，本文采用工程中常见取值进行研究。

(2) 沟槽底部开挖宽度B的取值主要根据施工要求进行确定，各规范无明确要求。《给水排水管道工程施工及验收规范》(GB 50268—2008)[17]中规定当无设计要求时，可以通过式(10)计算。

B=D0+2(b1+b2+b3) 。

(10)

式中：D0为管道外径；b1为管道一侧的工作面厚度；b2为管道一侧的支撑厚度；b3为模板的厚度。

本文采用3 m的管径，若按GB 50268—2008，则B可取4.4 m；美国土木工程师学会[18]推荐取值2倍管径即B=6 m，但当管径很大时，该推荐值会偏大。本文适当扩大B的取值范围取1.33～2.33倍管径(4～7 m)进行研究。

(3) 沟槽侧壁倾角α的取值通常根据现场地质、施工等条件确定。GB 50268—2008根据施工过程中土的类别规定了最陡沟槽侧壁倾角在38.66°～84.29°之间。大直径管道工程中常用倾角通常在60°左右，本文适当扩大倾角α的取值范围，即取30°～90°进行研究。

为考察这些因素对钢管变形及应力的影响，选取钢管最大竖向变形ΔD为变形的试验指标，选取3个特征点处环向弯曲应力，即管顶处环向弯曲应力σ1、管腰处环向弯曲应力σ2、管底处环向弯曲应力σ3，为应力σ的试验指标。模型中各参数之间无交互作用，根据表4中的试验因素和水平个数，选择L16(45)正交表安排试验，并将试验得到的指标结果ΔD、σ1、σ2、σ3列于表5。

4 正交试验结果分析

根据正交试验所得试验指标结果，以下分别采用极差分析法和方差分析法对结果进行分析对比。

4.1 极差分析法

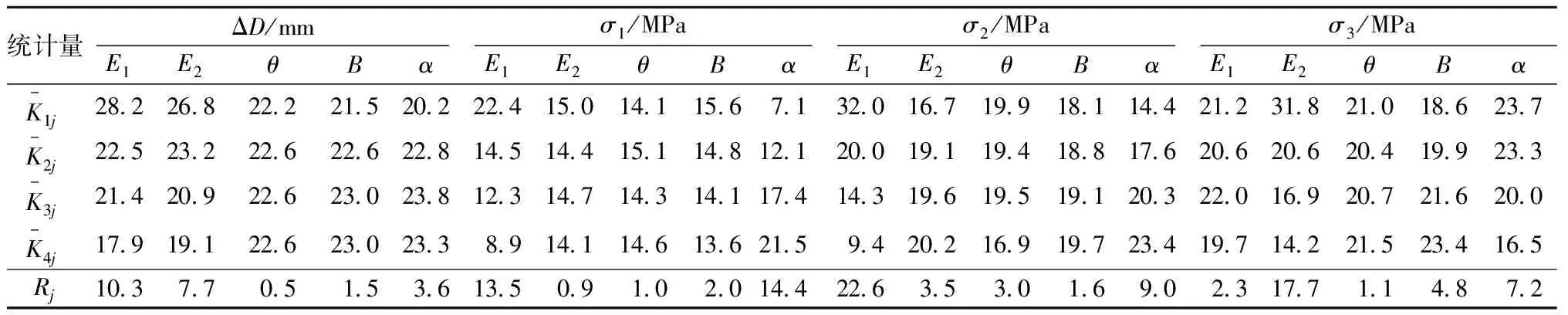
表6 ΔD、σ1、σ2、σ3影响因素极差分析结果Table 6 Range analysis results of test indices ΔD, σ1, σ2, and σ3

4.1.1 钢管变形分析

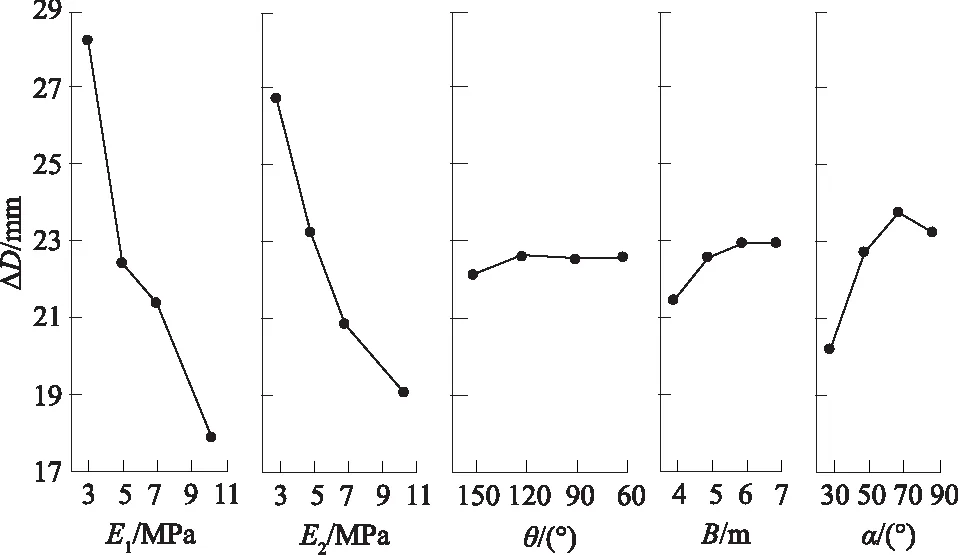
图3 因素-ΔD趋势线Fig.3 Trends of factors versus ΔD

(1)回填土及垫层模量增加后，钢管变形急剧减小，是影响钢管变形的主要因素，这是由于埋地钢管可看作是钢管与管周土体共同构成的联合承载体，土体变形模量的大小反映了管周土体的密实度，高密实度的土体可以增强对钢管变形的约束能力，进而减小钢管变形。砂垫层的主要作用是使钢管管底受力更为均匀，避免应力集中，垫层包角对钢管变形影响极小，不是主要影响因素。

(2)沟槽底部开挖宽度的增加会加大钢管变形，但当宽度增加到一定程度后，钢管变形基本保持不变，这是由于沟槽宽度的增加，会增加管顶土压力，并降低管侧土体综合反力模量，进而加大钢管变形，但随着沟槽宽度的增加，其影响越来越小。

(3)沟槽侧壁倾角对钢管变形有着较大的影响，随着侧壁倾角的减小，存在以下3种影响因素：管顶土压力变大、侧壁的约束作用减缓和管侧土体的约束能力增强。侧壁变缓后，钢管两侧沟槽内的土体在重力的作用下，沿着侧壁向下滑动，产生向钢管方向力的作用，进而约束钢管变形。此外，侧壁越缓，钢管两侧沟槽内的土体越多，产生向钢管方向的力越大，约束能力越强，但管顶土压力增幅和侧壁的约束能力越小。钢管变形随着倾角的增加，通常当沟槽窄时，可能存在先上升后下降的过程；但当沟槽宽时，钢管变形总体呈上升趋势。

4.1.2 管壁应力分析

同样，根据表6分析结果，绘制出因素-σ趋势图，如图4。由图4可以看出：

(1)回填土变形模量的增加，可以显著的降低σ1、σ2，垫层变形模量的增加可以显著的降低σ3，这是由于回填土变形模量的增加减少了管顶和管腰的弯曲变形，而垫层变形模量的增加能够显著降低管底的弯曲变形。

表7 ΔD、σ1、σ2、σ3影响因素方差分析结果Table 7 Analysis of variance of test indices ΔD, σ1, σ2, and σ3

(2)垫层包角对钢管特征点位置处的应力影响不大，但当材料性质相差较大时，可能在垫层材料交界处形成局部应力集中。

(3)沟槽底部开挖宽度对σ3有较大的影响，并随着沟槽宽度的增加，管底弯曲变形加剧。沟槽侧壁倾角通过影响钢管变形，进而对特征点的弯曲应力产生较大的影响。沟槽倾角变缓时，由于钢管两侧土体沿侧壁向钢管方向滑动，对钢管底部约束作用增强，管底弯曲变形降低，导致弯曲应力减小。

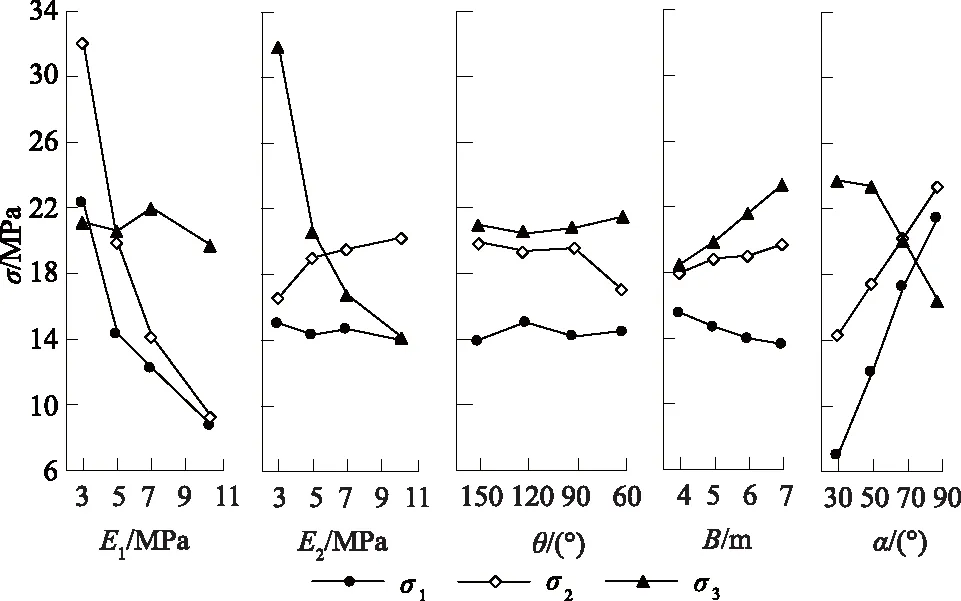
图4 因素-σ趋势线Fig.4 Trends of factors versus σ

4.2 方差分析法

由于正交表中无空白列，故可在平方和Sj中选择相对较小的平方和作为误差，进行方差分析[10]。根据正交试验所得的钢管最大竖向变形ΔD和环向弯曲应力σ1、σ2、σ3，结合方差分析理论，将分析结果列于表7。方差分析的检验水平置信度选用α=0.05和α=0.01，在F分布表中查出：F0.05(3,3)=9.28，F0.01(3,3)=29.5。因素的显著水平判断标准为：当Fj比>F0.01(3,3)时，该因素影响高度显著，敏感性高，记为“**”；当F0.01(3,3)≥Fj比≥F0.05(3,3)时，该因素影响一般显著，敏感性中等，记为“*”；当Fj比≤F0.05(3,3)时，该因素影响不显著，敏感性低[19]。

对ΔD而言，由F比大小可知：参数敏感性由高到低依次为E1、E2、α、B、θ，其中E1、E2、α对ΔD的影响高度显著，敏感性高；B对ΔD的影响一般显著，敏感性中等；θ对ΔD的影响不显著，敏感性低。

对σ1而言，由F比大小可知：参数敏感性由高到低依次为α、E1、B、θ、E2，其中α、E1对σ1的影响高度显著，敏感性高；B、θ、E2对σ1的影响不显著，敏感性低。对σ2而言，参数敏感性由高到低依次为E1、α、E2、θ、B，其中E1、α对σ2的影响高度显著，敏感性高；E2、θ、B对σ2的影响不显著，敏感性低。对σ3而言，参数敏感性由高到低依次为E2、α、B、E1、θ，其中E2、α对σ3的影响高度显著，敏感性高；B对σ3的影响一般显著，敏感性中等；E1、θ对σ3的影响不显著，敏感性低。

综上，通过方差分析法可知，对钢管变形和应力而言，敏感性较高的因素有E1、E2、α；B、θ的敏感性较低，但B的敏感性大于θ。从上述分析可知，方差分析法与极差分析法所得结论基本一致。

5 结 论

工程实践中，埋地钢管大多采用浅埋方式，大直径钢管也有较多应用，随着引调水工程的迅速发展，未来水利水电行业中大直径埋地钢管的应用将会越来越多。本文以具有埋深浅、直径大特点的某埋地钢管作为研究对象，引入正交试验法，系统研究了回填土变形模量E1、砂垫层变形模量E2、垫层包角θ、沟槽底部开挖宽度B和沟槽侧壁倾角α对钢管变形及应力的影响。研究结果表明：

(1)各因素对钢管变形的敏感性程度由高到低依次为E1、E2、α、B、θ，对钢管应力的敏感性与钢管部位有关：对σ1而言，参数敏感性由高到低依次为α、E1、B、θ、E2；对σ2而言，参数敏感性由高到低依次为E1、α、E2、θ、B；对σ3而言，参数敏感性由高到低依次为E2、α、B、E1、θ。

(2)综合各因素对钢管变形及应力的敏感性程度可知，敏感性较高的因素有E1、E2、α；B、θ的敏感性较低，但B的敏感性大于θ。

(3)回填土和垫层的变形模量是影响埋地钢管结构的最主要因素，设计及施工过程应尽可能地提高管周土体变形模量。此外，沟槽的形态参数如沟槽底部开挖宽度及沟槽侧壁倾角也对钢管结构产生较大的影响，应引起重视。