有压管道内串列管道双车的运移速度

贾晓萌，孙西欢，李永业

(太原理工大学水利科学与工程学院，山西 太原 030024)

传统运输方式因其资源消耗大、环境污染严重、运输成本高等缺点，已经不能满足当今社会所提倡的节能环保的发展理念，因此发展新型运输方式势在必行[1-2].而筒装料管道水力输送技术因其环境污染小、所需人力少、占地资源少等优点，符合当今社会的发展需求.筒装料管道水力输送技术是对囊体管道水力输送技术的优化和改进，通过在料筒两端添加支撑体使管道车在管道内做同心运动，避免了料筒和管道内壁的碰撞，降低了管道车与管壁之间的摩擦.经过数十年的研究与发展该技术已经取得了一定的理论和成果.

ZHANG等[3]建立了单个管道车在管道中做同心水平运动时的数学模型，根据数学模型计算管道单车的运行速度并推导出相应压降公式，并通过相应的物理试验验证了公式的准确性.文献[4-5]对静止状态下的管道单车所形成的同心环状缝隙流场进行了数值模拟，得到了环状缝隙内流速和压强的分布规律.ASIM等[6]分别对单个管道车在平直管道和弯管处运动时的流场变化进行了数值模拟，参考数值模拟结果对管道车输运系统进行了优化.文献[7-9]对不同雷诺数、径长比和荷重条件下单个管道车运移时的水力特性进行了研究，得出不同工况条件下管道车运移速度和管道内压力变化规律，并计算了相应的能耗损失.张春晋等[10]对不同导流条安放角下的管道车动边界环状缝隙流场特性进行了研究，发现随着导流条安放角的不断增大，动边界环状缝隙内流速和压强值均呈现出逐渐增大变化趋势.随着对单个管道车研究的不断深入和完善，学者们逐渐将工作重心转向管道双车的研究.吴剑等[11]对不同车间距条件下静止管道双车的车间轴向流速进行了研究，结果表明随着车间距的不断增大，车间轴向流速逐渐趋于稳定，当车间距为90cm时，双车之间的相互影响可以忽略.JIA等[12]对不同车间距下静止管道双车的水力特性进行了研究，发现当双车间距大于4倍的车身长度后，管道双车之间的相互影响可忽略不计.根据目前研究成果，筒装料管道水力输送技术的研究大多集中于单车的车速、流场以及能耗等方面，且对于管道双车的研究也都集中在静止状态下的流场分布变化，而运动状态下的管道双车的研究内容鲜有报道.

管道车作为筒装料管道水力输送的核心部件,其输送速度的快慢及稳定性对筒装料管道水力输送的技术研究至关重要，管道车速度直接决定着输送物料的数量并进而影响到筒装料管道水力输送的输送效率.因此，文中通过物理模型试验对影响管道双车运移速度的各因素进行研究，并分析各因素对管道车运移速度的影响程度，从而为管道双车结构优化提供参考，为寻求该技术所要求的最佳输送速度提供一定的理论基础.

1 试验系统和方案

1.1 管道车结构

管道车模型主要由料筒、支撑体2部分组成，具体如图1所示.料筒用于盛放物料，一般为圆柱体结构，用和管道相同材料的有机玻璃制成.在管道车两端每隔120°装有一个不锈钢材质构成的支撑体，前后共6个支撑体，支撑体用来保证管道车在管道中做同心运动，同时减小管道车与管壁的碰撞和摩擦.为了保持管道双车在运行过程中的车间距不变，试验在双车之间添加轻质弹簧，用于确定双车之间的间距.试验过程中为了避免弹簧拉伸和压缩，减少弹簧对双车之间流场的影响，同时又能确保管道双车顺利驶过弯道，选取线径为1 mm，外径为5 mm的弹簧进行连接.

图1 管道双车设计Fig.1 Two-pipe line vehicles design

1.2 试验系统

试验系统主要由动力装置、调节装置、投放和接收装置以及测试装置4部分构成，如图2所示,动力装置为离心泵；调节装置则由闸阀和电磁流量计组成；测试装置包括红外线计时器.试验管路总长24.7 m，管道内径100 mm，由透明有机玻璃管构成.试验管路分为前部直管段、弯管和后部直管段，前部直管长为7.5 m，后部直管段长10.8 m，弯管长为3.1 m.

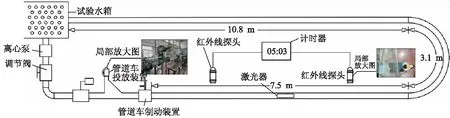
图2 试验系统Fig.2 Test system

试验开始前先将水箱注满水，启动离心泵将水箱中的水注入管道中，调节闸阀将流量控制在20 m3/h之下，之后通过投放装置将管道双车注入管道内，再次调节闸阀达到试验所需流量值，等管道内水流稳定后启动管道车制动装置，管道车在水流推动下在管道内运动，当管道车经过第一个红外线探头时，计时器开始计时，当管道车经过第二个红外线线探头时计时器停止计时，最后根据速度公式求取管道双车的运移速度.

1.3 试验方案

由于试验变量较多，每次控制单一变量，多次试验求取平均值.试验变量包括管道车尺寸l×D(D为单个管道车直径，l为单个管道车车长)，雷诺数Re，输送荷重m以及双车车间距L.管道车尺寸l×D分别为100 mm×80 mm，100 mm×70 mm，100 mm×60 mm，150 mm×80 mm，150 mm×70 mm，150 mm×60 mm；雷诺数Re为115 513，154 018，192 522， 238 107，对应的流量分别为30，40，50，60 m3/h.输送荷重m分别为400，600，800，1 000，1 200，1 600， 2 000 g.管道双车间距L分别为50，100，150，200， 250，300 mm.

2 试验结果分析

2.1 雷诺数对管道双车运移速度的影响

当管道尺寸和荷重一定时，雷诺数变化会引起管道内流量的改变，而流量的变化则会使管道内压力发生变化，从而对管道车的受力状况产生影响，进而影响管道双车的运移速度.因此，以型号为150 mm(l)×70 mm(D)，荷重为600 g，车间距为100 mm的管道双车为例，分析其在不同雷诺数下的运移速度变化，具体如图3所示.

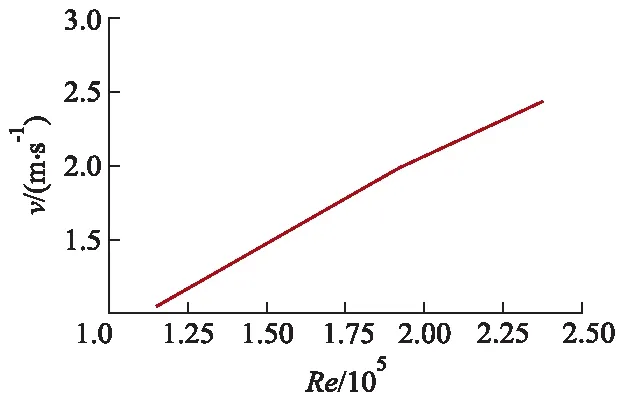
图3 不同雷诺数下管道双车运移速度图Fig.3 Moving speed of two-pipe vehicles under different Re

从图3中可以发现，当其他变量保持不变时，随着雷诺数的增大，管道双车的运移速度也逐渐增大，且管道双车运移速度与雷诺数呈线性增长的关系.这主要是由于管道双车在管道内运移时的主要动力来源于管道内水流的压力，而随着雷诺数的不断增大，管道内压力也逐渐增大，则管道双车动力也逐渐增大；虽然随着雷诺数的增大，管道双车所受阻力也逐渐增大，但是阻力随雷诺数的增大程度小于压力的增大程度，所以管道双车所受总动力随雷诺数增大是呈现逐渐增大的变化趋势，因此管道双车的运移速度随着雷诺数的增大而逐渐增大.

2.2 管道车尺寸对管道双车运移速度的影响

管道车的尺寸主要是指管道车的直径D和车身长度l，管道车尺寸的变化会使管道双车的受力面积发生改变，进而影响管道双车的受力，最终导致管道双车运移速度也发生改变.因此，试验选取管道双车荷重为400 g，车间距为100 mm，流量为40 m3/h时，不同尺寸下管道双车运移速度的变化情况进行研究，具体如图4所示.

从图4中可以看出，不同尺寸下的管道双车运移速度各不相同.当其他变量保持不变时，随着管道车直径D的不断增大，双车的运移速度也逐渐增大.这主要是由于管道双车前后端面所受的压差力为其运动的主要动力，由式(1)可知压差力与管道车前后端面的面积成正比，所以随着直径的增大，管道双车所受压差力逐渐增大；同时根据式(2)可知，当管道双车直径增大时，管道双车所受浮力也增大，而当输送荷重一定时，浮力的增大导致管道车所受摩擦力降低，因此随着管道车直径的增大，管道双车所受总动力也逐渐增大，管道双车的运移速度也增大.

Fp=Δp·Ac=Δp·πD2/4，

(1)

Ff=μFg=μ(mg-Fv)，

(2)

式中：Fp为管道车前后端面压差力；Δp为前后端面的压强差；Ac为管道车端面面积；Ff为管道双车所受摩擦力；μ为摩擦阻力系数；Fv为管道双车所受浮力；m为荷重.

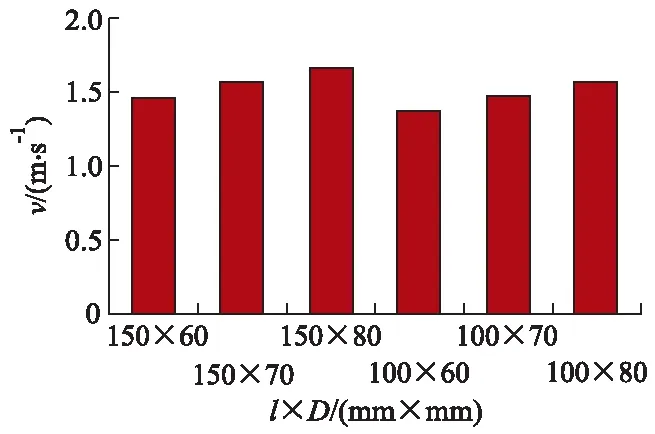
图4 不同尺寸下管道双车运移速度图Fig.4 Moving speed of two-pipe vehicles under different sizes

从图4中还可以看出，当其他变量保持不变时，车身长度较长的管道双车的运移速度也较快.由于试验过程中环状缝隙流流速大于管道车运移速度，因此环状缝隙流对管道车表面的剪切力为动力.根据式(3)可知，当管道车车身长度增加，车身壁面所受剪切力也增大，同时由于车身长度的增加，管道车的体积增大，浮力也随之增大，管道双车所受摩擦阻力降低，因此管道双车的总动力增加，管道双车的运移速度也增大.

Fτ=A′·τ=πDl·λρ(va-vc)2/8,

(3)

式中：A′为管道车侧面积；Fτ为管道车侧壁面所受剪切力；τ为管道车侧面所受切应力；λ为流动阻力系数；ρ为水的密度；va，vc分别为环状缝隙流流速和管道车运移速度.

2.3 输送荷重对管道双车运移速度的影响

输送荷重的多少一直是筒装料管道水力输送技术关心的另一个重点.当荷重过大时，虽然一次性可输运较多的物料，但是其运输速率降低；而当荷重较小时，一次性输送物料的重量减少，但是其运输速率提高.因此，文中以型号为150 mm(l)×80 mm(D)，输送流量为40 m3/h，车间距为100 mm的管道双车为例，研究不同荷重对管道双车运移速度的影响，具体如图5所示.

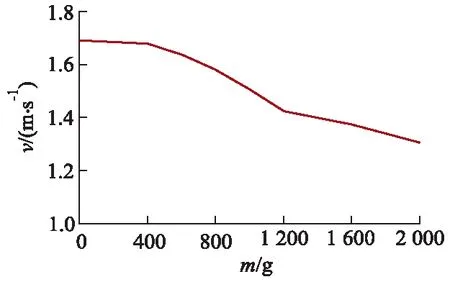
图5 不同荷重下管道双车运移速度图Fig.5 Moving speed of two-pipe vehicles under different loads

从图5中可以看出，随着输送荷重的增大，管道双车的运移速度呈现逐渐降低的变化趋势.这主要是由于当管道双车尺寸一定时，管道双车所受压差力和浮力均保持不变，根据式(2)可知，当荷重增加后，管道双车所受摩擦阻力增大，进而使得管道双车所受的总动力值降低，因此，管道双车的运移速度随之降低.从图中还可以看出，以荷重1 200 g为分界点，当输送荷重小于1 200 g时，管道双车的运移速度随荷重增大时的降低速率较快，即曲线斜率较大，而当输送荷重大于1 200 g后，管道双车的运移速度随荷重增大时的降低速率变小，即曲线斜率较小.

2.4 不同车间距对管道双车运移速度的影响

当管道双车之间的间距不同时，双车之间的相互影响程度也会不同，进而也会对双车的运移速度产生影响.因此文中以车型为150 mm(l)×70 mm(D)，输送流量为40 m3/h，荷重为400 g的管道双车为例，研究不同车间距对管道双车运移速度的影响，具体如图6所示.

图6 不同车间距下管道双车的运移速度图Fig.6 Moving speed of two-pipe vehicles under different vehicle spacing

从图6中可以看出，随着管道双车车间距的不断增大，管道双车的运移速度呈现出逐渐增大的变化趋势，且不同车间距下的管道双车运移速度小于单个管道车(车间距为0时)在管道内运移时的速度.这主要是由于当管道双车在管道内运移时，水流经历了“满管-环状缝隙-车间-环状缝隙-满管”的流动过程，能耗损失比单个管道车在管道内运移时的大，管道双车所获得的动能要小于单个管道车的，因此使得管道双车的运移速度小于相同工况下的单个管道车运移速度.当管道双车间距较小时，所形成的车间空间也较小，水流自环状缝隙进入车间之后流速迅速发生改变，水流与管道车之间的相互作用也较为剧烈，因此造成的能耗损失也较大，进而使得管道车的运移速度较低，而随着车间距的逐渐增大，水流进入车间后与两车的相互作用逐渐减弱，能量损失也随之降低，管道双车的运移速度也逐渐增大.当车间距在50～150 mm时，随着车间距的增大，管道双车的运移速度增长较快，而当车间距在150～250 mm时，随着车间距的增大，管道双车的运移速度增长较慢，之后随着管道双车间距的进一步增大，管道双车之间的相互作用几乎可以忽略不计，可将管道双车在管道内的运动看成是单个管道车的运动，双车的运移速度也向单个管道车在管道内运移时的速度转变.

3 各因素对管道双车运移速度影响

由以上试验结果可以看出，管道双车的运移速度受到管道车直径、车身长度、雷诺数、输送荷重以及车间距的影响.为了探究这5个因素对管道双车运移速度的影响程度，采用多元回归分析中的标准回归系数法进行分析.

对于随机变量Y来说，受到m个自变量X1，X2，…，Xm的共同影响，试验样本容量为n.记Xik表示自变量Xi在第k次试验时的取值，Yk表示随机变量Y在第k次试验的结果，如果Y和Xi之间存在线性关系，则回归方程可记为

Y=a+b1X1+b2X2+…+bmXm.

(4)

公式(4)中的回归系数bi由下列方程组求出：

(5)

为了消除试验过程中自变量所取单位的影响，Y对Xi的标准回归系数b′i与Y对Xi的回归系数bi之间的关系式为

(6)

经过式(6)的处理，标准回归系数b′i与Y及Xi所取单位无关，因而可以直接进行比较.|b′i|值越大，Xi对Y的影响就越大.

依据上述理论，试验相关数学模型为

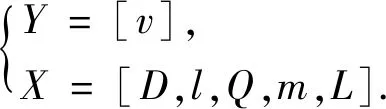
(7)

管道车直径D取60，70，80 mm, 管道车长度l取100和150 mm，雷诺数取为115 513，154 018，192 522，输送荷重m取400，600，800 g，管道双车车间距L取50，100，150 mm，5个变量两两正交，试验次数为162次，根据试验数据计算管道双车的平均运移速度.将各项数据代入相关方程，求解得到对应的标准回归系数b′i依次为b′1=0.302 00，b′2=0.115 00，b′3=0.935 00，b′4=-0.093 80，b′5=-7.85×10-4，由此可知|b′3|>|b′1|>|b′2|>|b′4|>|b′5|

通过标准回归系数法的计算可知，雷诺数Re，管道车直径D，车身长度l，输送荷重m，双车车间距L对管道双车运移速度的影响程度依次降低.

观念摄影在装置作品中的应用越来越普遍，而且，随着摄影设备的更新发展，图像质量越来越高。法国艺术家首次提出了在装置作品中应用观念摄影艺术品，其首次设计的艺术品与一般的摄影作品相比更具有独特性。一般的摄影技术中，由于图片是单面的，所以对于场地的选择非常严格，并且还限制了人们对作品的想象和观看，因此，通过摄影作品和装置的结合，就极大的融合了多种不同空间、不同时间等，对于作品内涵的表达有很大帮助。就现在观念摄影在装置方面的分类，主要包括更好的刻画图片的内涵的图片为主，实物为辅类；分散或者依附于实物表面的实物和场景为主类；单纯依赖于图片相互之间的空间关系的完全脱离实物类；

由以上分析可以看出管道双车的运移速度受到多个因素的影响，因此，在以后的试验研究过程中要综合考虑多方面因素影响，选择较为合适的管道车尺寸、车间距、雷诺数以及输送物料荷重，争取在获得较大运移速度的同时消耗较少的能量.

4 结 论

文中通过物理试验对影响管道车运移速度的各因素进行了研究，并采用标准线性回归分析了各因素对管道双车运移速度的影响程度，所得结论如下：

1) 管道双车的运移速度随着雷诺数的增大而增大，二者呈线性增长关系.

2) 不同尺寸下的管道双车运移速度也各不相同，管道车直径或者长度的增大，均会引起管道双车运移速度的增大，这其中型号为150 mm×80 mm的管道双车运移速度最大.

3) 管道双车运移速度和输送荷重呈负相关关系，即随着输送荷重的不断增大，管道双车的运移速度逐渐降低.

5) 雷诺数Re，管道车直径D，车身长度l，输送荷重m，双车车间距L对管道双车运移速度的影响程度依次降低.