拼接梯度压电材料中多裂纹的响应问题
2021-08-11周春梅
周春梅, 马 旭, 闫 洁
(宁夏师范学院数学与计算机科学学院, 固原 756000)
梯度压电材料作为一种新型的复合智能材料,兼具压电和梯度二者的优点,被广泛应用于诸多工程领域。材料的复合虽然克服了单项材料的缺陷,但又有许多新的问题需要解决。例如,如何判定裂纹在这种新型材料中的稳定性是一个值得关注的课题。一般的金属材料,都考虑用动应力强度因子、能量释放率、能量密度因子作为断裂分析的依据.对于裂纹扩张来说,当材料呈脆性或小范围承受时,应力强度因子通常作为断裂的依据。薛宇等[1]针对传统压电构建容易被破坏的问题,提出了一个改进的功能梯度材料特性分布形式,研究了材料分布类型、梯度分布指数和材料总体积分数对材料板振动控制的影响。张智娟等[2]研究了一种悬臂梁双晶压电能量采集装置的发电性能,实验将两片双晶压电振子并联,得到振动台频率、激励位移等对装置输出电压和负载功率的影响情况。刘婷等[3]介绍了4类压电材料的研究进展,分析了它们的结构特点、制作方法和应用场合,并且展望了压电材料的未来发展趋势。李林利等[4]讨论了恒定温度场下压电材料矩形板的频率和振幅,给出了温度对位移的影响,以及速度、加速度的变化规律。穆翔等[5]研究了傅里叶变换在压电材料与热电材料的接触、断裂等问题中的应用。刘媛等[6]利用有限截项法分析了无限板圆孔边四不等长裂纹,得到应力强度因子的接近程度与裂纹半长与半径比有关。祝青钰等[7]研究了椭圆孔边任意长度双裂纹复合型应力强度因子复变函数解。提出了一种基于Muskhelishvili复变函数理论和有限截项原则的强度因子求解方法,得出强度因子受椭圆孔半轴比、夹角和裂纹长度的综合影响。梁瑞虹等[8]分析并制造了宽温堿低损耗的新型压电材料与摩擦功能材料,提岀了通过相结构调控、增加第三组元、引入偶极子缺陷钉扎畴壁等方法来制备低损耗压电陶瓷材料。李洁等[9]研究了一种用于压电传感器的柔性电极的制备及其性能分析。朱帅等[10]利用有限元模型,采用分层法进行材料的梯度仿真模拟,分析了功能梯度压电材料单裂纹的受力情况,得到缓解应力集中的参数算例结果。现对拼接压电材料中的共线多裂纹问题进行分析。
1 问题描述及理论分析
如图1所示,在x-y平面中,梯度压电材料(functionally graded piezoelectric material,FGPM)拼接在一均匀压电材料(piezoelectric material,PM)上,材料沿Z轴极化。裂纹位于高度为h1+h2的梯度压电带y=0的平面上,裂纹间距为2c,裂纹的长度为|bj-aj|=2a0,设第j个裂纹的左右尖端在x轴的坐标分别为aj、bj,裂纹表面处有反平面应力载荷τxy=τ(x)、平面内的电位移Dy=D(x)。
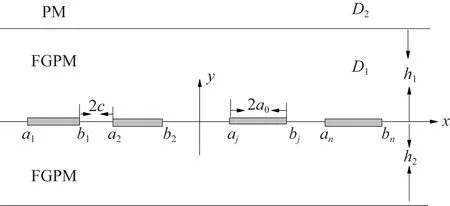
图1 拼接梯度压电材料中共线多裂纹模型
压电材料的本构方程为
(1)
(2)
式中:τxz(i)、τyz(i)和Dx(i)、Dy(i)分别为应力和电位移;wi和φi为位移和电势;i(i=1,2) 分别对应区域D1和D2;c44(i)、e15(i)、ε11(i)分别为弹性刚度系数、介电常量、压电常量。
电场分量与电势有如下的关系:

(3)
假设梯度压电材料的弹、电性系数沿y轴按指数函数分布:
[c44(1)(y),e15(1)(y),ε11(1)(y)]=
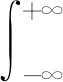
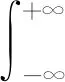
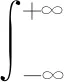
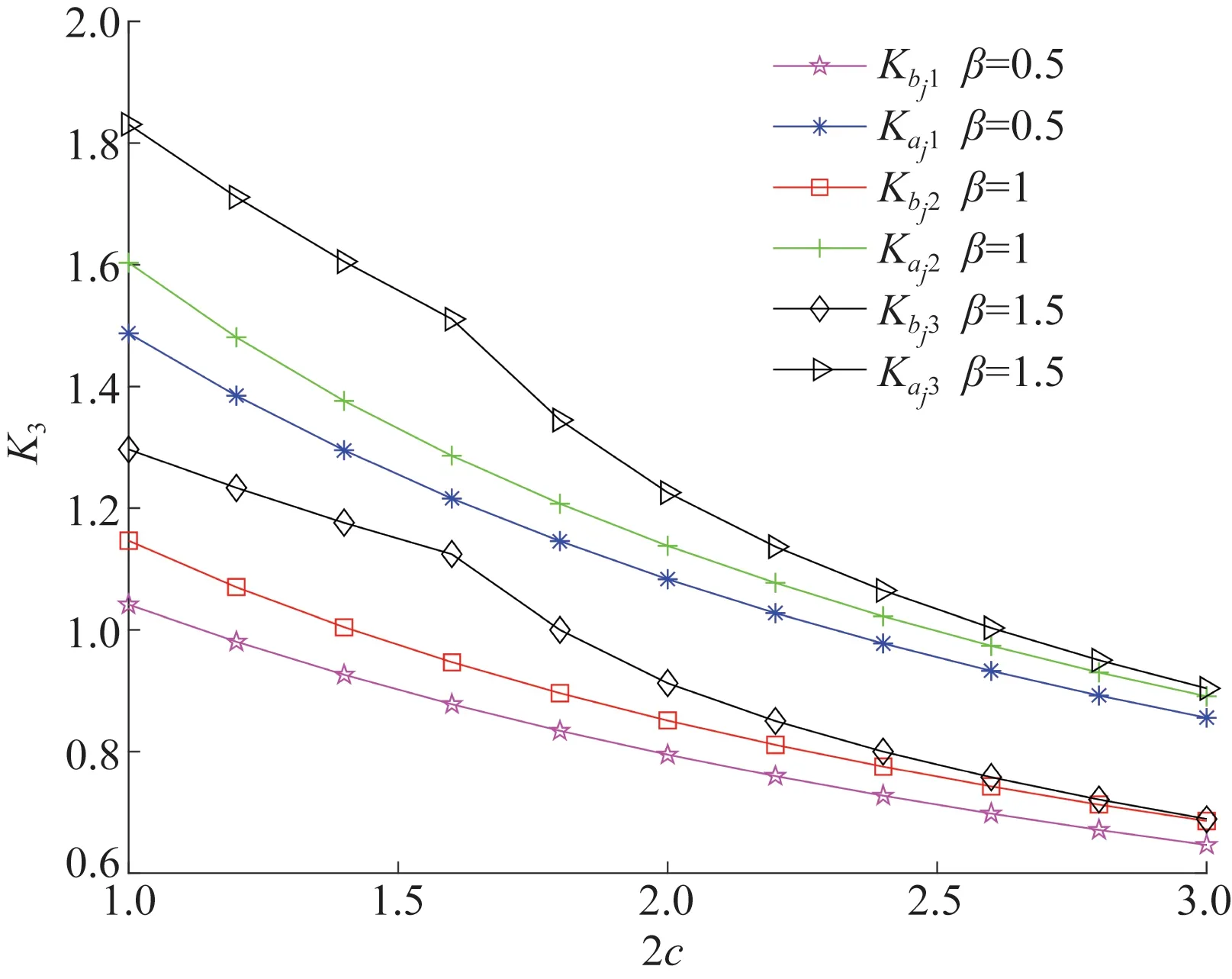
eβy[c0,e0,ε0], -h2 (4) [c44(2)(y),e15(2)(y),ε11(2)(y)]= eβh1[c0,e0,ε0],y>h1 (5) 式中:β、c0、e0、ε0分别为功能梯度参数、剪切模量、压电系数、介电常数。 静态平衡方程为 (6) 由式(1)~式(6),得到控制方程为 -h2 (7) (8) 由此可得 (9) (10) 式(9)和式(10)解的形式为 (11) -h2 (12) (13) 式(11)~式(13)的未知函数的表达式为 (14) 由于材料结构关于y轴对称,只需要考虑右半平面。边界条件及连续性条件[11]为 (15) (16) (17) 运用傅里叶变换,并且利用边界条件式(15)~式(17),得到下列方程: A1(α)ep1 h1+A2(α)ep2 h1-E1(α)e-αh1=0 (18) B1(α)ep1 h1+B2(α)ep2 h1-F1(α)e-αh1=0 (19) +αF1(α)e-αh1]e-iαxdα=0 (20) ×ep2 h1+αF1(α)e-αh1]e-iαxdα=0 (21) e-iαxdα=0 (22) e-iαxdα=0 (23) p1D1(α)-p2D2(α)]e-iαxdα=0 (24) p2D2(α)]e-iαxdα=0 (25) 引入两个位错函数[12]s1(x)和s2(x): (26) (27) 将应力和电势的解代入式(26)、式(27)中,并结合边界条件有 (28) x∈[aj,bj]时,可得 C1(α)-C2(α)]e-iαxdα (29) D1(α)-D2(α)]e-iαxdα (30) 应用Fourier变换法和边界条件式(15)~式(17)式求解方程组,解出系数Ai(α)、Bi(α)、Ci(α)、Di(α)、E1(α)、F1(α)。再由本构方程和边界条件得到应力和电位移的解析表达式[13]为 (31) 当α→∞时,k有奇异项被分离,可以表示为 (32) 令 (33) 将式(32)、式(33)代入式(31),方程被标准化为 (34) (35) (36) 通过Gauss-Chebyshev积分公式对第一类奇异积分方程式(34)和式(35)进行求解。基函数与权函数有如式(37)所示关系: (37) 式(34)、式(35)通过简化为Chebyshev多项式求解。 (38) (39) (40) 最后解得裂纹端切应力强度因子和电位移强度因子[15]为 (41) (42) (43) (44) 式中:未知函数的值Fj(-1)(j=1,2)和Fj(1)可以分别从Fj(tn-1)、Fj(tn-2)、Fj(tn-3)和Fj(t2)、Fj(t3)、Fj(t4)的二次插值得到。 裂纹端强度因子正则化[16]为 (45) (46) 取PZT-4为基本压电材料,通过数值计算,可以得到以下一些结论。 从图2得到正则化强度因子与裂纹长度2a0的变化规律。第j个裂纹的左端aj处的强度因子比裂纹右端bj处的强度因子大。随着带宽比h1/h2的增大,裂纹左右端处的强度因子逐渐增大,从图形可以看出,强度因子是平行的增大趋势。当带宽比的值固定不变时,裂纹端的强度因子与裂纹长度2a0有同样的变化趋势,即裂纹长度增大时,强度因子也增大。 从图3得到正则化强度因子随带宽比h1/h2的变化规律。可以看出与图2有相似的结论,裂纹左端处的强度因子比裂纹右端处的强度因子大。随着非均匀参数β的增大,裂纹左右端的强度因子逐渐增大,并且也是平行的增大趋势。当非均匀参数β固定不变时,裂纹端的强度因子随着带宽比h1/h2的增大而减小。 图2 不同带宽比下,裂纹长度与正则化强度因子的响应 图3 不同非均匀参数下,带宽比与正则化强度因子的响应 从图4得到正则化强度因子随裂纹间距2c的变化规律。与前面的结论一致,裂纹的左端处的强度因子比裂纹右端处的强度因子更大。随着非均匀参数β的增大,裂纹左右端的强度因子逐渐增大,这里可以看到,当β=1.5时,线条有跳动的趋势,不再是平行的变化情况。当非均匀参数β的值固定不变时,裂纹端的强度因子随着裂纹间距2c的增大而减小。 图4 不同非均匀参数下,裂纹间距与正则化强度因子的响应 讨论了拼接压电材料中共线多裂纹问题。利用傅里叶变换技术将边值问题转化为积分方程,应用位错函数以及高斯-切比雪夫方法求解方程获得裂纹端的切应力和电位移的解析式。最后的数值分析结果显示们,裂纹端强度因子与裂纹几何长度、裂纹间距、材料带宽比以及非均匀梯度参数的关系密切。图2~图4有统一的结果,即裂纹左端的强度因子总比裂纹右端的强度因子大。随着带宽比以及非均匀梯度参数的增大,裂纹端强度因子也随之增大;当带宽比有确定值时,裂纹长度增大时,强度因子也增大;当非均匀梯度参数有确定值时,带宽比和裂纹间距增大时,强度因子反而减小。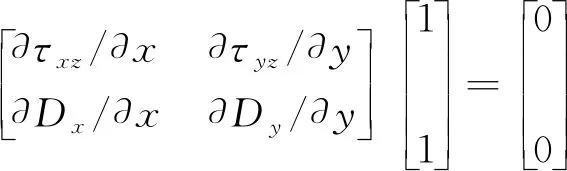

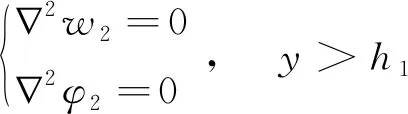

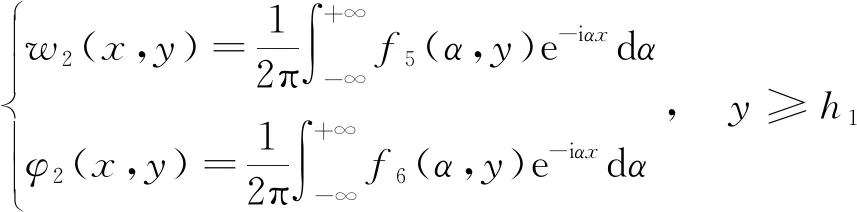

2 问题求解
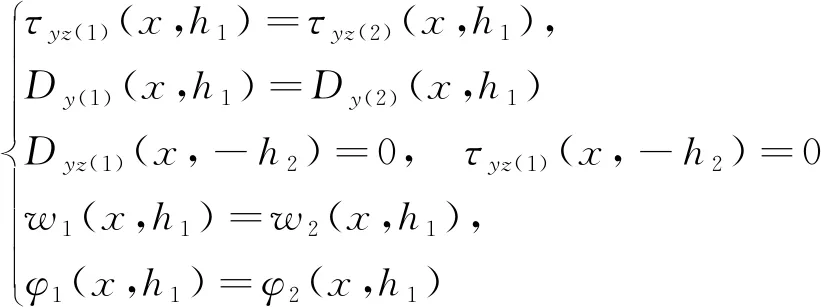












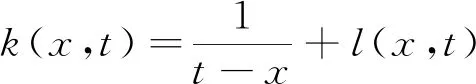
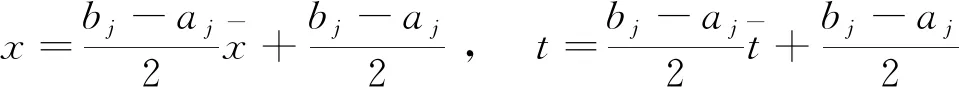
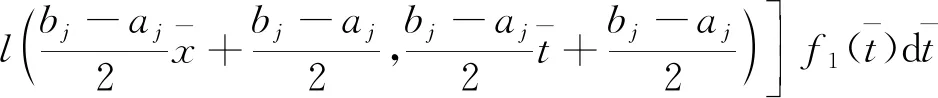
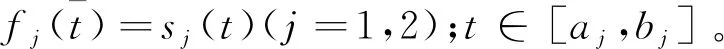
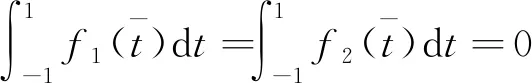
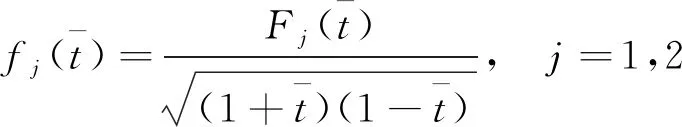
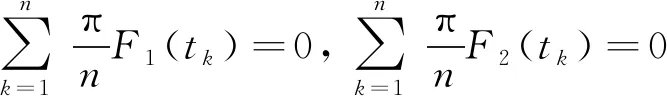
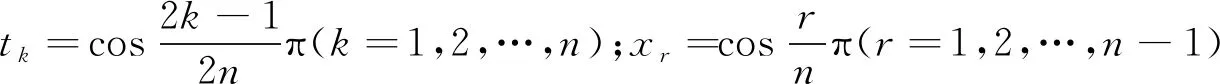
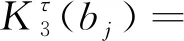
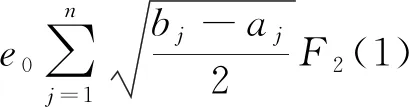
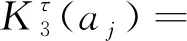
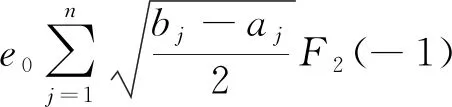
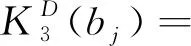
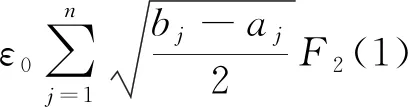


3 数值计算及讨论
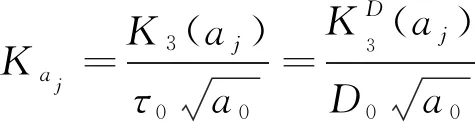



4 结论
