基于6自由度平台的体感模拟算法研究

王军政，蒋铄，汪首坤，沈伟

(1.北京理工大学 自动化学院，复杂系统智能控制与决策国家重点实验室，北京 100081； 2.北京理工大学 自动化学院，伺服运动系统驱动与控制工信部重点实验室，北京 100081)

提 要： 针对模拟驾驶器对动感逼真度和平台工作空间的需求，将基于洗出算法的体感模拟控制策略应用于6自由度并联式运动模拟器.首先对系统进行了整体设计及数学建模，然后通过分析人体感知机理，提出了基于加速度控制的体感模拟洗出算法；随后具体研究了模拟驾驶过程中可能存在的多种复杂工况及对应的加速度控制模式；最后，通过联合仿真与实验验证了所提出控制算法的可行性及控制效果，结果显示平台在有限运动范围内动感逼真度得到了显著提升.

运动模拟器在航天、航海及车辆驾驶等领域中得到了广泛应用[1]，早期的运动模拟器工作空间小、承载能力低、驱动方式多为液压式且缺乏能够模拟复杂环境的视景系统，随着近年来虚拟现实技术的兴起，运动模拟器可用于模拟驾驶系统研发、作战飞行员辅助训练、促进VR动感娱乐装置及汽车测试样机等产品开发[2]. 除对系统控制精度、平台负载能力及结构稳定性的要求外，模拟车辆驾驶过程中能否给与操作者真实的动感逼真度及不同工况下模拟驾驶运动平台的控制性能成为了运动模拟器研究领域中的热点[3-5].

体感模拟洗出算法作为运动模拟控制的核心技术之一，有效地提升了并联式平台运动过程中的动感模拟逼真度. 上世纪90年代，KIM等[6]采用简单的洗出滤波器针对Stewart平台进行有限范围内的运动模拟，但无法有效量化评估人体感知并进行参数设计，本世纪初BARBAGLI等[7]将经典洗出算法应用于电动车模拟系统的研发，通过不断调整和优化滤波器参数打破了并联式平台工作空间的限制，实现了一定程度上的动感模拟，但在非极限工况下系统响应还不够明显. 近年来，BEGHI等[8]设计出用于航空飞行器的体感洗出算法，基于模型预测控制的方式，在线进行滤波器及控制器参数预测试图实现复杂工况下的体感模拟，但可变参数较多，无法保证通讯实时性，仍欠缺系统可靠性.

为解决以上问题，设计了一款Stewart型6自由度动感模拟器，创新采用改进形式的体感模拟洗出算法. 搭建Linux交叉编译环境并建立5G路由器基站，将Unity3D城市道路视景系统中的路况信息转化为摇摆台的6自由度运动指令进而验证算法的有效性. 实验结果表明，平台在有限工作空间的运动提升了操作者的动感体验.

1 系统组成与原理

本文研究的动感模拟驾驶器实验样机如图1所示，由并联式6自由度平台、座椅、视景系统、嵌入式主控制器、PMSM电机驱动器、通讯基站、传感器测量装置以及惯性负载组成.

6自由度平台是结构基础，其主要执行机构为6根力位复合一体化电动缸. 电动缸通过十字万向节铰接上下平台，内嵌PMSM电机、增量式光电编码器、应变片式拉压力传感器等，将伺服电机转子与传动丝杆一体化，在实现力位复合控制的同时可满足疲劳试验要求，提高了传动效率及可靠性.

主控选用Linux多任务交互式实时操作系统实现交叉编译的同时提升了平台的动态响应速度，利用5G路由器基站可提升视景系统、手机移动终端、

图1 动感模拟器样机Fig.1 Dynamic simulator prototype

上位机与主控间的数据传输效率. 编码器脉冲经差分输入、光耦隔离、加减计数将位移信息送入主控；力传感器经标定校准、放大调理将力信号送入主控，主控利用SPI串行模块结合DA向驱动器发送指令驱使电动缸伸缩. 视景系统在Unity3D2019环境下配合C#脚本语言完成场景绘制、车辆模型搭建，多传感器数据的采集、滤波与融合，通过UDP协议以固定格式指令传输虚拟运动体的姿态信息给主控，进而实现与6自由度平台的联动.

2 系统建模

2.1 一体化电动缸传动环节

PMSM电机作为一体化电动缸的重要传动环节，由定子、转子、电枢铁芯等构成，鲁棒性强，具有较硬机械特性，建立永磁同步电机在d-q轴的方程如下

(1)

式中：ud和uq分别为定子d、q轴定子电压；id和iq分别为d、q轴的定子电流；Ld和Lq分别为定子绕组自感；P为微分算子；Ra为定子绕组电阻；φf为定子磁链幅值；ωn为磁场旋转角速度. 根据系统运动特性有

(2)

式中：pn为极对数；J为系统的转动惯量；Te为电磁转矩；TL为负载转矩；ωr m为电机输出轴机械角速度.id=0时，可联立各式得电机简化数学传函[9]

(3)

式中：KT为伺服电机转矩系数；Teq为交叉角频率的倒数；G(s)为二阶滞后环节，由于电机内部结构复杂及负载受诸多干扰因素等原因需利用参数辨识法估计.

滚珠丝杠启动力矩小，无爬行，能实现精确微给进，若仅考虑黏性摩擦，与电机间联轴器视为刚性连接，不考虑回程间隙，根据文献[10]，可建立传动方程如下

(4)

式中：Jm为总转动惯量；cb，ct分别为旋转部件与轴向黏性摩擦系数；ls为丝杠导程；K为刚度系数；xl为缸杆位移；θm为丝杠转角.

2.2 6自由度平台数学建模

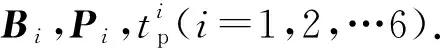
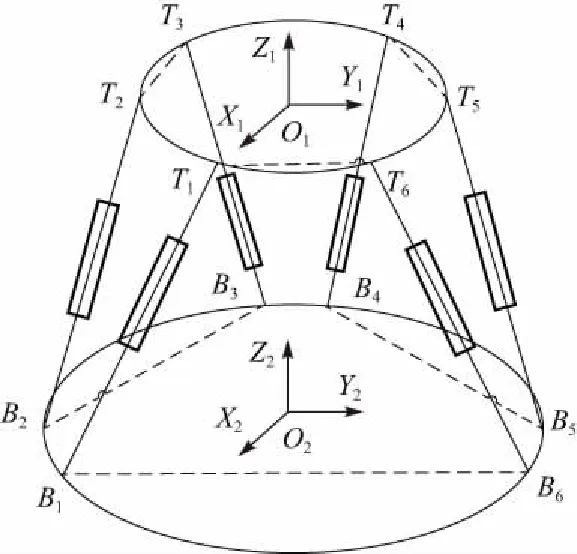
图2 6自由度平台模型Fig.2 Six-degree-of-freedom platform

T=T(x,θx)Τ(y,θy)T(z,θz)

(5)

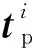
(6)

式中Lmin为电动缸伸出中位时的长度[11].

体坐标系下用角速度ω描述姿态变化，在惯性坐标系下则用欧拉角变化率描述，需将体坐标系下运载工具角速度信号转变为惯性坐标系下欧拉角变化率，即

(7)

为进行6自由度位置正解以实时计算平台位姿，采取Levenberg-Marquardt法求解非线性方程组F(x)=0

F(x)=f(θx,θy,θz,x,y,z,ui)-li，i=1,2,…6

(8)

式中：ui为驱动器控制量；li为初始缸长.

首先取u0=‖F(x0)‖,x0为初始迭代点，按下式求解搜索方向d

(JTJ+u0I)d=-JTF

(9)

式中J为雅可比矩阵，通过泰勒展开获得.

随后，采用0.618一维搜索法搜索最优迭代步长λ，求取φ(λ)局部极小值,其中

φ(λ)=F(x0+λd)

(10)

0.618黄金分割法计算过程中可实时更新步长，Levenberg-Marquardt法可有效改善Gauss-Newton迭代法对雅可比矩阵列满秩的限制条件，且能够提高计算效率. 最后计算增量并更新x0的值，并按特定规律更新u0进行迭代，可得平台6自由度参数.

3 人体感知器

人体感知系统主要由视觉、前庭系统和触觉感受器组成. 前庭器官包括半规管与耳石器，其中半规管用来感知角速度变化，例如车辆前倾与转弯，耳石器用来感知加速度，例如车辆启动、制动及在崎岖路面上的颠簸，耳石器对加速度感觉以比力形式呈现，即线加速度与重力加速度的矢量和. 加速度与角速度低于某阈值时人体不会察觉到运动，利用这一特点可设计运动模拟器回归中位而不被模拟器驾驶员察觉的方式[12].

耳石与半规管数学模型对人体感知进行量化，有助于为体感模拟算法相关参数的设计提供参考，耳石器传递函数表达式如下

(11)

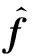
表1 耳石模型参数Tab.1 Otolith model parameters

半规管传递函数表达式如下

(12)

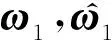
表2 半规管模型参数Tab.2 Parameters of semicircular canal model

4 体感模拟洗出算法

基于加速度控制的体感模拟洗出算法控制系统原理如图3所示，图中f为视景系统惯性坐标系下的三轴比力输入，ω为实际驾驶器的角速度输入，θin为模拟驾驶路面倾角，T为欧拉角旋转矩阵，L为角速度变换矩阵，FHP1,2为二阶高通滤波器，FLP1为二阶低通滤波器，G(s)为加速度控制器，其确定了加速度与目标位移之间的联系. 洗出算法的作用是利用摇摆台有限的运动工作空间还原真实运动过程中的动感，系统最终输出为6自由度平台的位移l与角度θ.

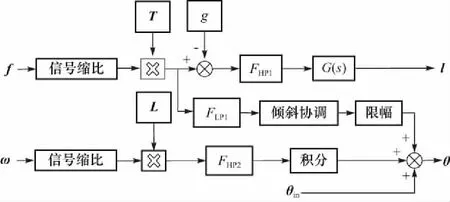
图3 体感模拟算法控制原理Fig.3 Control principle of somatosensory simulation algorithm

4.1 输入信号缩比

首先需对输入的模拟驾驶系统加速度和角速度信号进行缩比以调节平移量，采用非线性缩比策略可保证整个区域信号连续性的同时，对不同幅值段信号实现不同幅度缩放，美国NASA兰利探究中心的航天飞行模拟器也曾采用这种方法，通常为三阶多项式法，其形式为

y=a3x3+a2x2+a1x+a0

(13)

式中：x为输入信号；y为输出信号；a0～a3为各阶次系数. 非线性缩比策略的作用是防止6自由度平台超出运动范围，随后将缩比信号经矩阵变换到体坐标系下.

4.2 加速度分解策略

当操作者模拟驾驶于平滑路面或崎岖不平道路，需分别设计对应的控制策略，因此要将体坐标系中加速度信号进行高低频分解. 在振动工况及角速度过滤环节选用二阶高通滤波器，表达式如下

(14)

式中：ξ为阻尼系数；ωs为震荡频率；k′为常数量纲一. 过滤出的高频信息输入到加速度控制器中. 在模拟平滑路面行驶情况时，加速度呈现低频特性，利用二阶低通滤波环节将其滤出，表达式如下

(15)

4.3 倾斜补偿策略

模拟持续加速、减速及连续转弯过程时，需将平台沿各自轴向倾斜角度以获取重力加速度分量. 比力信号经低通滤波得到的加速度低频稳态分量与重力的矢量夹角可补偿人体耳石感受到的持续加速度. 补偿倾角为

(16)

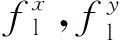
(17)

4.4 加速度控制器实现

崎岖不平路面驾驶过程中加速度信号呈现高频抖动，6自由度平台垂直向等效为弹簧阻尼器，列出线性时不变单自由度振动运动力平衡方程

(18)

式中：m为惯性负载质量；b为阻尼系数；k为弹簧常数；ag为垂直向加速度. 电动缸阻尼力与弹性恢复力与其相对速度和位移有关[13].

在坠落撞击的过程中，等效为单位脉冲激振力作用，表现出宽频带特性，其通解为

式中：ω0为系统固有频率；ε为临界阻尼比.

5 实验结果与分析

为验证所提出控制算法的可行性及控制效果，在Solidworks、Adams中依据实验样机建立图4所示的机械模型并进行动力学分析，结合Matlab实现体感模拟算法，进行联合仿真，并在图1所示的实验样机中进行测试. 机械模型如图4所示，系统参数如表3所示.

图4 动感模拟器机械模型Fig.4 Mechanical model of motion simulator

表3 平台结构参数Tab.3 Parameters of platform’s structure

图5为操作者模拟车辆连续快速地经过5组10°的标准化斜坡，给定为俯仰向周期性正弦运动，利用上位机采集驱动器控制量与电动缸伸缩速度进而得出实时姿态，通过前馈PID控制以提升电动缸的伺服控制精度. 图5为运动时的动态跟踪曲线，轨迹方程为

θy(t)=10.0sin(4πt)

(20)

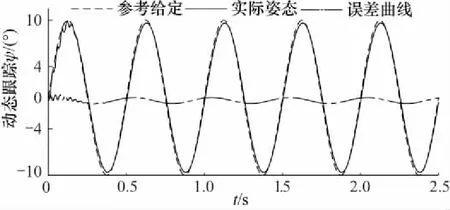
图5 斜坡工况跟随测试Fig.5 Slope condition following test

通过最小二乘参数辨识法近似得出电动缸传动环节传递函数为Gc(s),表达式为

(21)

图6为模拟崎岖不平路面振动工况的6自由度平台位移与单缸速度曲线. 改变加速度高通通道二阶震荡频率ωs，对比ωs为0.5，1.0，2.5时的实验结果，可以看出，当ωs较小时，6自由度摇摆台超出限制，但运动速度过快，容易引发电动缸失控，如图7所示. 经反复调试，ωs取2.5时，随着ωs的逐渐增大，平台能够实现有限运动范围内振动模拟，且能够在模拟器运动结束后回归0位.

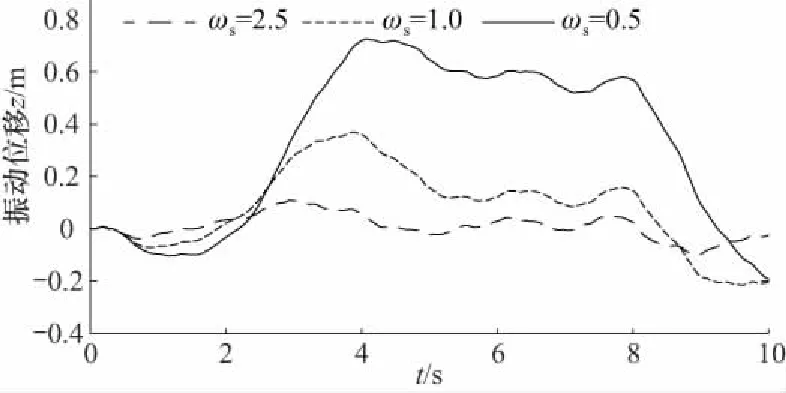
图6 崎岖路面振动工况测试Fig.6 Vibration test of rough road

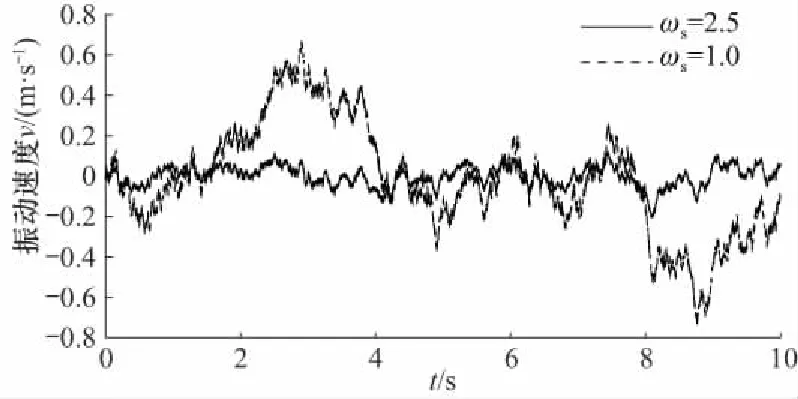
图7 振动工况下电动缸速度Fig.7 Electric cylinder’s speed under vibration condition

图8为倾斜补偿实验测试曲线，在视景环境下模拟货车的启动过程，最大加速度约为2 m/s2,从实验曲线看出，在第4 s时，加速度达到最大，摇摆台做出俯仰向后倾约12°的倾角，符合预期，而未采用倾斜补偿的俯仰角仅来自于模拟驾驶器自身的倾角，无法还原真实环境下的动感. 在10 s时，速度达到最大，驾驶器进入匀速运动阶段，倾角归0.

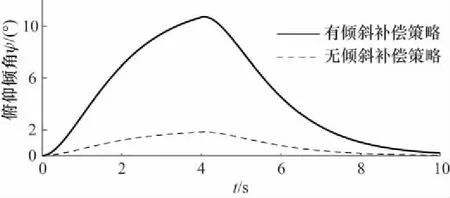
图8 倾斜补偿测试Fig.8 Tilt compensation test condition

6 结 论

为满足运动模拟器在有限运动空间下尽可能真实的还原驾驶操作者在模拟驾驶过程中的动感模拟需求，搭建了基于一体化电动缸执行单元的6自由度运动模拟器实验平台，并设计了基于人体感知器的体感模拟洗出算法，对视景环境下的振动工况进行了策略分析，针对车辆启动加速工况采取了倾斜补偿策略，通过联合仿真与对比实验，验证了系统的可行性及体感模拟控制效果. 下一步工作将深入研究复杂工况下的并联式稳定平台伺服控制方法.