地铁牵引电机气动噪声仿真关键因素研究*

王文庆， 朱一乔， 惠新伟， 张 伟

(中车永济电机有限公司，陕西 西安 710016)

0 引 言

随着电机在多种领域上的应用，噪声已经成为电机研发的一项重要性能指标[1]，电机噪声过大不但会影响人的舒适性，还会对周边环境造成噪声污染，降低电机噪声是电机应用过程中重点关注的问题。

牵引电机作为高铁、地铁等地面交通工具核心动力部件，其工作时产生的噪声主要由3部分组成：气动噪声、电磁振动噪声和机械噪声[2-4]，其中气动噪声是自通风牵引电机的主要噪声源。因此，在电机设计研发阶段，能够准确预估产品噪声数值成为保证电机声品质的有效手段，而仿真的精确度也成为影响噪声数值的关键因素。

在电机气动噪声仿真计算中，噪声的计算涉及到多个参数，包括噪声计算模型的声学网格数量、声源区噪声向自由场中辐射的插值阶次以及当地温湿度下空气介质属性等，这些参数与设置不但对噪声计算的准确性有影响，而且也会影响噪声计算的效率。在实际的工程问题中，仿真计算应兼顾精确度和分析效率。

本文以1台地铁自通风异步牵引电机为例，针对噪声计算中涉及到的关键参数进行研究，为电机气动噪声仿真计算及修正提供指导。

1 气动噪声仿真

1.1 计算原理

旋转机械气动噪声计算基于Lighthill声类比方法[5-7]，并加入了Curle’s理论[8]：Curle方程的体积分作为有限元区域的体源；Curle方程的面积分作为边界条件；自由场的格林函数作为其他的边界条件。应用分部积分产生弱变分形式表示为

(1)

∑ij=ρvivj+(ρ-ρ0)δij-τij

(2)

在处理工程气动噪声过程中，ACTRAN采用混合计算气动声学(CAA)方法[9-11]，该方法将气动噪声计算分为声源产生和声传播：

(1) 采用ANSYS FLUENT计算电机的非定常流场[12-13]，同时输出速度、密度信息。

(2) 以非定常流场计算结果为基础，利用Lighthill声类比方法进行计算，即不可压缩计算流体动力学(ICFD)模块通过Lighthill方程将风扇流场区域的速度、密度信息转换成气动声源再进行声场计算。

1.2 计算模型

1.2.1 CFD计算模型

电机气动噪声仿真过程中涉及到电机计算流体动力学(CFD)模型和声学模型，根据电机原始模型简化后的CFD模型包括静止域和旋转域，静止域为电机进风口及定子流体域图1(a)、出风口延长段图1(b)，旋转域为转子流体域图1(c)及风扇旋转域图1(d)。

图1 CFD模型

1.2.2 声学计算模型

电机声学模型分为声源区和声传播区，如图2所示。声源区为电机流体静止域，电机试验时是水平放置在地面的，因此对声传播区电机底部声学模型进行切除。

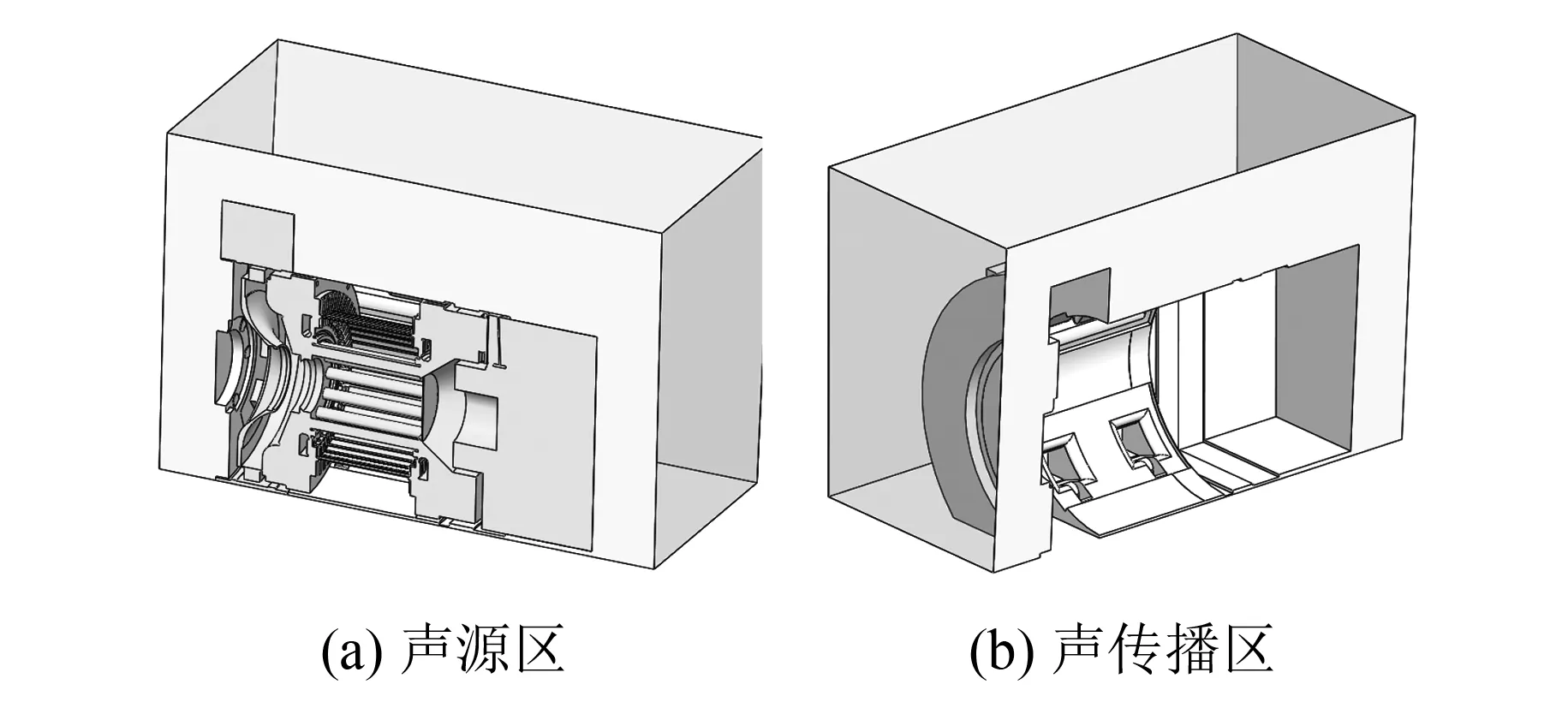
图2 声学计算模型

1.2.3 噪声测点布置

图3所示为电机噪声测试测点[14]分布示意图，根据相关测试标准[15]，关键测点数为5，竖直平面上测点位于电机中心位置距离电机外壳1 m处，水平面上距离电机外壳1 m处，前后左右均布4个测点。在仿真模型中，依据每一测点的空间坐标位置同样设置5测点。

图3中，h为电机轴中心轴高度；d=1 m；x为关键测量点。

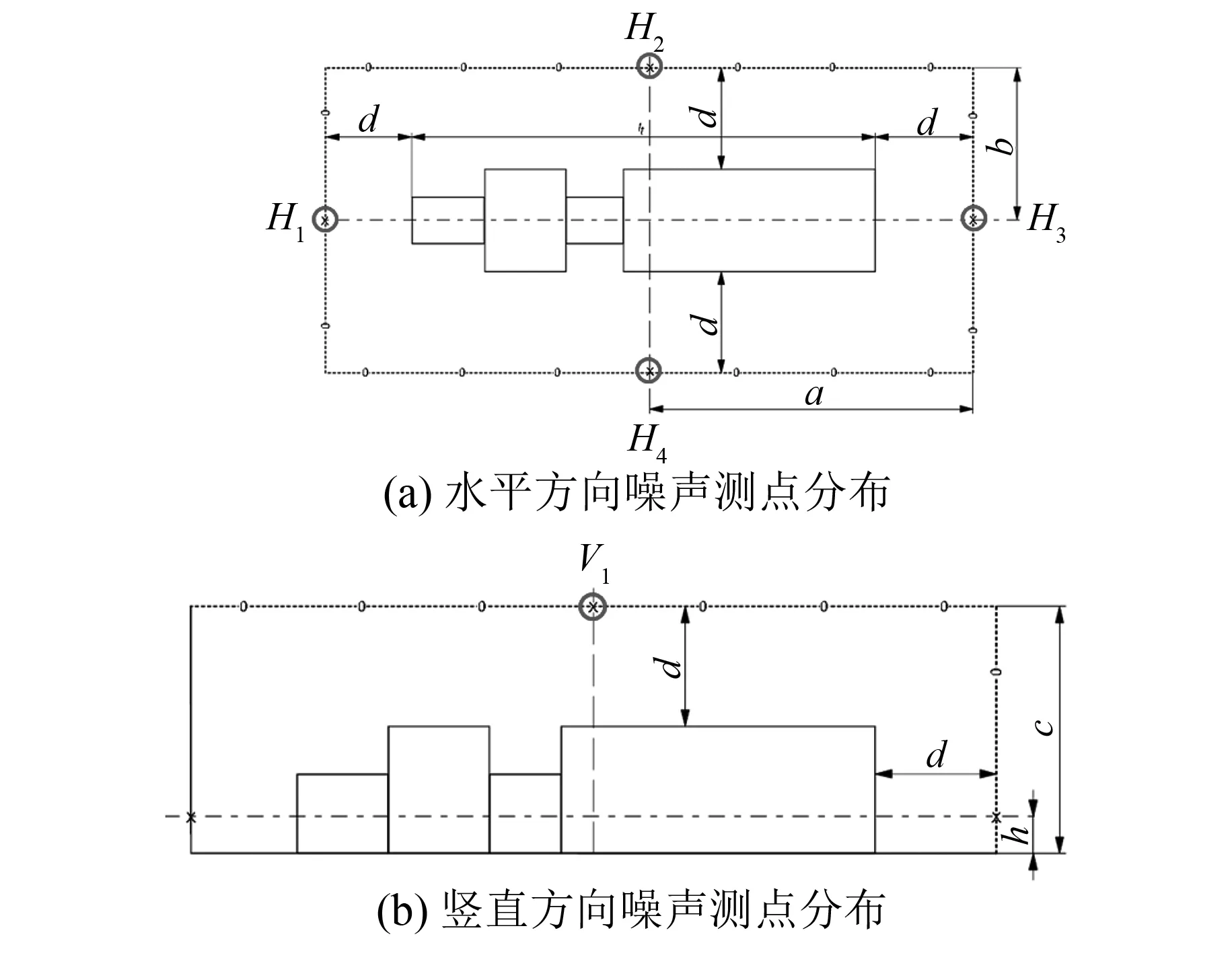
图3 电机噪声测点分布示意图

2 仿真关键因素

2.1 试验设置

试验根据噪声测试标准进行，试验过程中电机保持在额定工况下空载运行，额定转速为2 000 r/min，运行20 min后电机运行稳定后进行噪声测试。

相关试验参数设置如表1所示。

表1 试验参数

2.2 计算模型声学网格无关性验证

2.2.1 CFD计算模型

一般来讲，声学网格尺寸要大于流场网格尺寸。声学网格的大小由计算的目标频率决定，目标频率对应的则是风扇噪声的叶片通过频率fBP的3倍频，从以往经验来看为了保证采样精度往往在这个基础上再乘以2.5倍，因此最大计算频率fmax为

fmax=fBP×3×2.5

(3)

(4)

式中：n0为电机转速；N为风扇扇叶个数。

声学网格尺寸需要保证在最大频率对应波长内应包含8层网格。据此网格尺寸计算为，确定声波长λ；每个波长对应6～8个网格单元，通常取8个，具体计算如下：

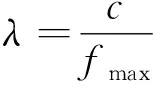
(5)

(6)

式中：λ0为声学网格单元尺寸；c为当地声速。

电机转速为2 012 r/min，扇叶个数为11，依据此网格划分方法，获得对应的最大计算频率fmax为3 000 Hz，λ0为14 mm。为提高采样精度，考虑网格相关性研究，同时采用最大计算频率为5 000 Hz进行对比分析，最终划分的网格数分别如表2所示。

表2 不同计算频率的网格数分布

2.2.2 试验与仿真结果对比

最大计算频率为3 000 Hz和5 000 Hz的声学网格对应的电机监测点处噪声计算结果与试验测试值分别对比，其中各测点值和多点平均值均为声压级(SPL)，工程应用中以声功率级结果作为最终参考依据，结果如表3所示。

表3 不同声学网格尺寸噪声仿真与试验结果对比

最大计算频率为5 000 Hz的声学网格的噪声计算结果与试验值相比，单个测点处最小相差0.1 dB(A)/H1，最大相差5 dB(A)/H2，多点平均值相差1.9 dB(A)；最大计算频率为3 000 Hz的声学网格的噪声计算结果与试验值相比，多点平均值相差2.1 dB(A)。图4可以更直观地看出，不同网格尺寸的噪声仿真计算结果在各个监测点上相差均很小，说明在电机气动噪声仿真计算中使用最大计算频率为3 000 Hz的网格能满足计算精度的需求。

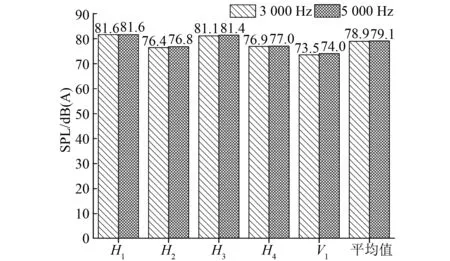
图4 不同测点处2种声学网格尺寸的噪声结果对比

2.2.3 计算所需资源与时间对比

表4汇总2种声学网格尺寸所需的计算资源进行对比。计算时采用同样的计算机配置(128 GB内存/24核/48线程)，由于最大计算频率为5 000 Hz的声学网格数量明显增多，其所需的计算内存也明显增大，是最大计算频率为3 000 Hz的声学网格所需内存的2倍。在计算时间上，最大计算频率为5 000 Hz的声学模型所需计算时间也明显增大，是最大计算频率为3 000 Hz的声学网格所需时间的6倍。图5对比了2种声学网格尺寸模型在计算时所需的硬盘存储量，最大计算频率为5 000 Hz的声学模型所需的硬盘存储量约500 GB，是最大计算频率为3 000 Hz的声学网格所需存储量的5倍。

表4 不同声学网格所需资源对比

通过对比发现,使用8 mm的声学网格的噪声计算结果，与14 mm的声学网格计算结果相差较小，多点平均值相差2.1 dB(A)。但是在所需计算资源和时间上，相差很多，使用8 mm的声学网格的噪声计算时间多达3天11小时(83 h)，再加上电机非定常流场计算的时间，整个电机气动噪声计算时间可能多达10天以上，这在实际工程中很难接受。因此，考虑到计算时间和精度，在电机气动噪声计算模型中使用14 mm即最大计算频率为3 000 Hz的声学网格模型。

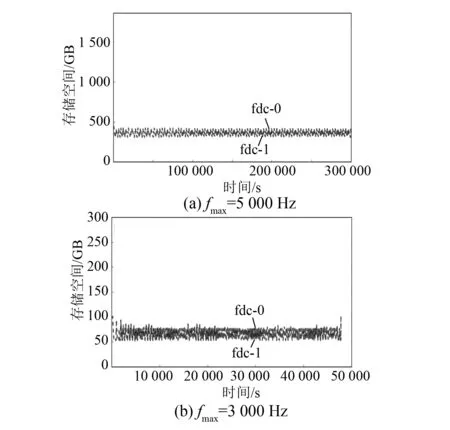
图5 不同声学网格尺寸的计算时所需硬盘存储空间对比

2.3 无限元插值阶次对气动噪声计算影响

2.3.1 参数介绍

在噪声测试中，麦克风常常需要布置在自由场中，比如一般的电机噪声测试中麦克风布置在距离电机外壳1 m远的位置。在噪声计算模型中，参考噪声测试时麦克风位置来设置噪声监测点，如果使用有限元方法需要建立足够大的模型，这样网格数量势必会很多，造成计算量过大。因此，为了提高声学计算效率，学者们提出了声学无限元法。声学无限元提供2种功能：(1)创造无反射边界条件。声波传递到无限元边界，不会发生反射。(2)允许计算远场声学响应。无限元可以帮助工程师提取计算域外监测点的声学响应。

ACTRAN提供了无限元声学组件来模拟声波向自由场传播的问题，无限元的定义主要输入：材料、插值阶次和椭球参考坐标系。其中插值阶次可以解释为无限元内振动声源产生的声场，可以看作由一系列的简单声源组合而成。

无限元的阶次是一种在无限元无限边界上定义一系列虚拟节点的方法。增加虚拟节点的数量可以模拟更复杂的辐射声场，但是同时会增大求解计算量。

2.3.2 试验与仿真结果对比

本文通过在ACTRAN中分别设置插值阶次为4、6、8，对比不同无限元插值阶次对噪声计算结果和计算效率的影响。表5列举了不同插值阶次的噪声计算结果与试验测试结果，发现不同插值阶次的单点和多点平均值与试验值相差基本一致。从图6中可以更直观地看出，不同插值阶次对噪声计算结果影响很小。

表5 不同无限元阶次的噪声仿真与试验结果对比

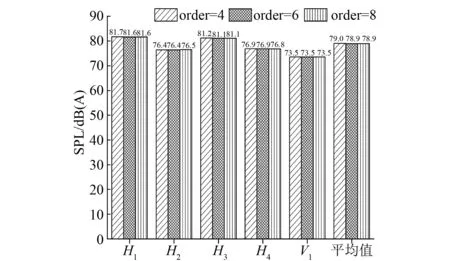
图6 不同无限元阶次噪声计算结果对比

2.3.3 所需计算资源与时间对比

表6汇总不同无限元插值阶次所需的计算资源进行对比。计算时采用同样的计算机配置(128 GB内存/24核/48线程)，从表6中可以看出，无限元插值阶次主要影响了计算时间，当插值阶次为4时，计算时间明显缩短。

表6 不同插值阶次噪声仿真所需资源对比

还可以发现，无限元插值阶次对计算精度的影响很小，但是在所需计算时间上，相差很多，当插值阶次为4时所需计算时间远小于其他2种阶次。因此，考虑到计算时间和精度，在电机气动噪声计算中推荐设置无限元插值阶次为4。

2.4 空气介质属性对电机气动噪声计算影响

2.4.1 考虑温湿度的空气密度与声速计算

在噪声传播计算中，需考虑空气介质属性。仿真计算过程中默认选择常温15 ℃下的空气介质属性(密度和声速)，但在实际测量中，随着温湿度的变化，空气的密度和声速是变化的。本文选用默认的空气介质属性和试验的实际数值进行对比分析。

噪声测试过程中现场实测温度为34.1 ℃，湿度为62.3%，可依据实测的空气温湿度值计算空气密度和声速。

影响空气密度的环境因素有气压、温度、高度和湿度。气压为干燥空气气压和水蒸气气压之和。干燥空气气压和高度有关，计算公式为

(7)

式中：标准大气压P0=101 325 Pa；常温为15 ℃;标准温度T0=15+273.15=288.15 K；温度递减率L=0.006 5 K/m；H为高度；理想气体系数R=8.314 47 J/(mol·K)；重力加速度g=9.806 65 m/s2；摩尔质量M=0.028 964 4 kg/mol。

当不考虑湿度时(即相对湿度取0%，为干燥空气)，空气密度仅与气压和温度有关，计算公式为

(8)

式中:ρ为10 min的平均空气密度；P为干燥空气平均气压；R0为干燥空气的气体系数，取R0=287.05 J/(kg·K)；T为测量温度，K，计算时取T=TC+273.15，TC为实际温度，℃。

非干燥空气时，基于特滕斯公式的饱和水蒸气压力为

(9)

式中:C0、C1、C2分别为特滕斯公式的系数，C0=6.107 8，C1=7.5，C2=237.3。

相对湿度定义为实际水蒸气压力和饱和水蒸气压力的比值，记为PH%。实际水蒸气压力为

PV=100Es·PH%

(10)

此时考虑湿度的空气密度计算公式为

(11)

由式(7)～式(11)可得，代入实测的温度34.1 ℃和湿度62.3%，计算得到考虑当地湿度的空气密度为1.086 9 kg/m3。

考虑温度的当地声速计算公式为

(12)

式中：c0为常温下声速340 m/s。

依据式(12)，计算得到考虑当地温度的声速为351.087 m/s。

2.4.2 试验与仿真结果对比

对比不同空气属性下电机噪声仿真和试验结果，如表7所示，可以看出，单个测点上仿真与试验值最小相差0.1 dB(A)，多点平均值相差2.3 dB(A)，这一误差和使用常温空气介质属性的仿真计算结果基本一致。从图7可更直观地看出，不同空气介质属性的噪声计算结果相差在0.1～0.7 dB(A)之间，区别较小，在后续的仿真计算中建议直接使用常温空气介质属性。

表7 不同空气属性的噪声仿真与试验结果对比

图7 不同空气属性噪声计算结果对比

2.5 误差分析

对比不同因素仿真结果与试验结果，发现均存在一定偏差。误差来源分析如下：(1)工程试验中，电机噪声测试是在车间进行，测试电机周围存在遮挡物(如电源、变流柜等设施)，造成噪声反射；(2)实际电机噪声测试过程中除了风扇气动噪声，还包括电磁噪声和机械噪声；(3)监测点位置的精确性。这些问题导致测试结果存在一定的偏差。

根据表3、表5、表7可知，仿真与试验结果误差均在3 dB(A)以内，因此仿真结果满足工程计算的要求。

2.6 参数验证

为了校核上述关键参数的可靠性，采用上述关键参数对相似自通风电机进行验证，同样采用额定工况(1 808 r/min)下空载运行并与试验结果进行比较，从表8可以看出，采用上述关键因素仿真计算的总声功率级结果与试验值相差1.5 dB(A)，满足仿真要求。

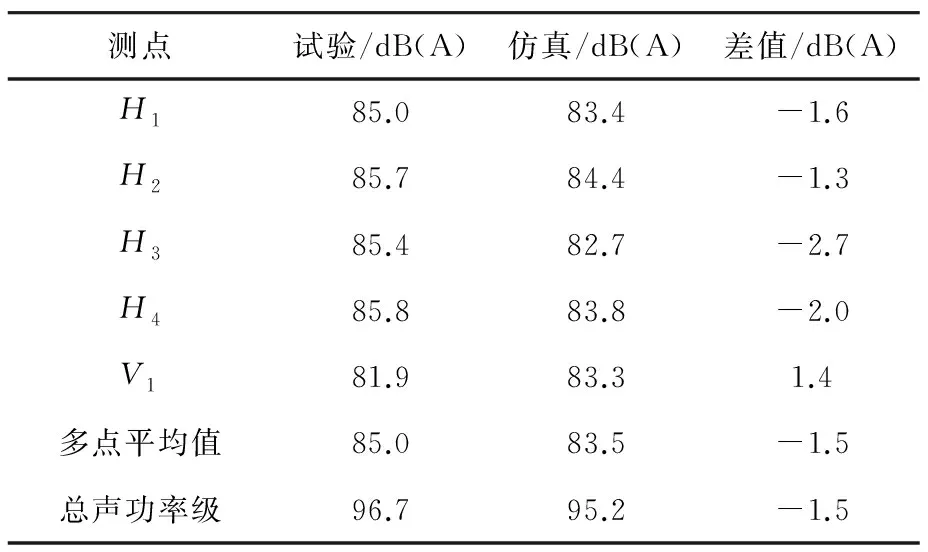
表8 验证电机噪声仿真与试验结果对比

同时，由图8可以看出，该电机在331 Hz处存在明显的离散峰值，其对应了额定转速下的风扇噪声的叶片通过频率fBP，仿真结果完全捕捉到风扇的特征频率，证明了仿真分析的准确性。图9展示了在fBP为331 Hz时，电机前后左右各方向在声传播区域内的声压分布。

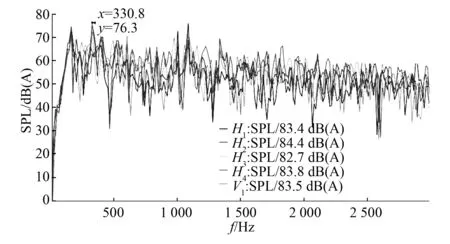
图8 验证电机各监测点仿真频谱图

图9 电机风扇噪声的叶片通过频率为331 Hz时的声压云图

3 结 语

本文以1台地铁自通风异步牵引电机为例，研究了气动噪声仿真计算中关键参数对噪声仿真精度和效率的影响，并对这些关键参数进行验证。采用ACTRAN软件分析了声学网格尺寸、声源区噪声向自由场中辐射的插值阶次以及当地温湿度下空气介质属性等不同仿真参数对电机气动噪声的影响，并与试验测试结果进行对比分析，结果表明：

(1) 在保证满足声场最低网格要求下的气动噪声仿真结果可以满足精度要求。

(2) 无限元插值阶次对计算精度的影响很小，推荐选用无限元插值阶次为4。

(3) 不同空气介质属性的噪声计算结果相差很小，建议直接使用常温空气介质属性。

(4) 仿真与试验误差控制在3 dB(A)以内，可以有效地进行电机噪声预测，为电机设计初期噪声优化设计提供可靠的依据。