基于Morris与Sobol法的SWMM模型参数敏感性分析
2021-08-10刘鹏霄马立山唐中楠王伊林
刘鹏霄 马立山 唐中楠 王伊林
(河北建筑工程学院,河北 张家口 075000)
0 引 言
近年来,我国经济发展迅速,城市化进程加快,城市的热岛效应随着城市化的发展而加剧,城市内涝频发[1].在此种情况下,水文模型的精确性为预测洪涝灾害,提早进行防范提供了可能[2].SWMM模型是由美国环保署研究的一个水文水质模型,它能够对于降雨从产生开始到形成径流等一系列过程进行模拟,在国内的众多水文模型中得到了广泛的应用[3].模型主要由结构和参数两部分组成,参数又可以分为纯物理参数、纯经验参数和半经验参数三类,对于模型而言,模型的参数选择对于模型的精确程度有很大影响[4].通过分析不同研究区的模型参数对于输出结果的影响程度,降低模型参数的不确定性,从而提高模型率定的效率与精度[5].
参数敏感度分析方法可以分为局部敏感性分析和全局敏感性分析两类[6].局部敏感性分析主要用于评价参数对于输出结果的局部影响,而全局敏感度分析则可以考虑到参数整体对于输出结果的影响,注重参数之间的作用对于输出的综合效应[7].局部灵敏度分析方法主要包括Morris筛选法、EFAST法、扰动分析法等,全局分析法包括Sobol法(方差分解法)、Extend FAST法、RSA方法(区域灵敏度分析方法)、GLUE法(普适似然度法)、RSMSobol法、逐步回归法、方差分析法等[8].史蓉等[9]利用Morris筛选法将SWMM的模型参数排序;张胜杰等[10]利用修正Morris筛选法对不同雨强下的参数进行敏感性分析,得出雨强与下渗参数关系;常晓栋等[11]利用Sobol法进行敏感度分析,认为此方法适应于城市水文模型敏感性相关研究;张质明等[12]将Sobol法应用于WASP模型得出模型参数之间耦合性强结论.就目前情况看,在对于模型参数进行敏感度分析时,一般只运用某一种方法,考虑单个参数影响,而未能将参数组合影响考虑进去,造成分析结果的偏差.本文选取总产流和峰值流量两相作为目标函数,利用Morris法和Sobol法两种局部与全局相结合的敏感度分析方法,对于研究区的SWMM模型进行分析.其研究结果有利于今后模型敏感度分析方法的选取,进一步提升模型的精度.
1 研究材料及方法
1.1 研究区域概况
研究区亚热带季风气候,日照时间长,历史平均气温15.43℃,年平均降水1170mm,因为属亚热带季风气候,受东南沿海暖湿气流影响,降雨本身存在明显季节性变化差异,夏季降雨占全年总降雨接近50%,全年的5月至9月份是暴雨高发期,这一段时间易形成洪涝灾害,并且持续时间长,危害性大.
1.2 研究区模型构建
研究区域面积为21.55km2.不透水区面积16.94km2,占总面积的78.60%.根据研究区域研究时间段的卫星影像、数字高程数据、土地利用现状和现状排水管网,利用GIS将研究区域面积、不透水比例、坡度、下垫面情况和管网信息输入到SWMM模型中,构建雨水径流模型,将整个研究区域划分为26个子汇水区、27个节点和17个排放口.子汇水区主要通过高程图和坡度图,与具体的主干道分布位置进行大的集水区的划分,经过人工调整后的子汇水区划分,输入降雨时间序列,添加雨量计,完成模型构建,如图1所示.
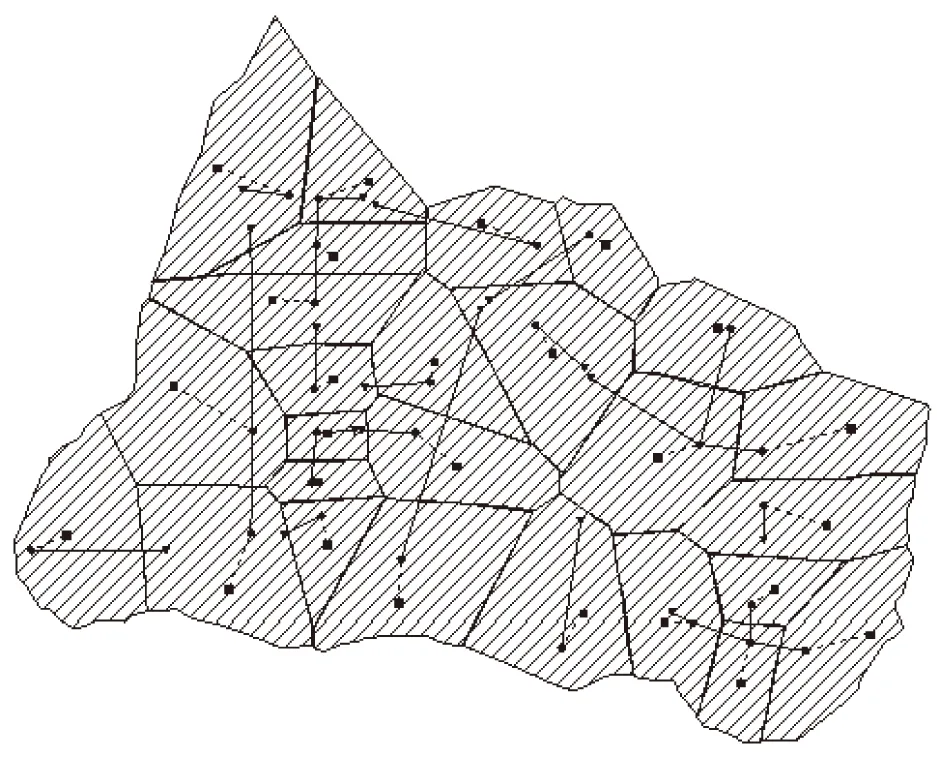
图1 SWMM模型图
1.3 模型参数与目标函数
1.3.1 模型参数
模型采用了Horton模型与非线性水库模型来模拟降雨径流过程,Horton模型需要参数主要包括:最大入渗速率、最小入渗速率、衰减速率常数、干燥时间、最大可能渗透深度[13].非线性水库模型所需参数主要包括汇水面积、不透水百分比、宽度、坡度、不透水区曼宁系数、透水区曼宁系数、不透水区积水深度、不发生积水百分率[14].其中,面积、宽度、坡度、不透水区域所占百分数、透水区不发生积水所占百分数等根据地理信息系统获取,排水管道的管网数据从排水资料和施工图中获取.根据现有资料的具体情况,现选择敏感性分析的参数共8项,其具体的物理意义和取值范围见下表:
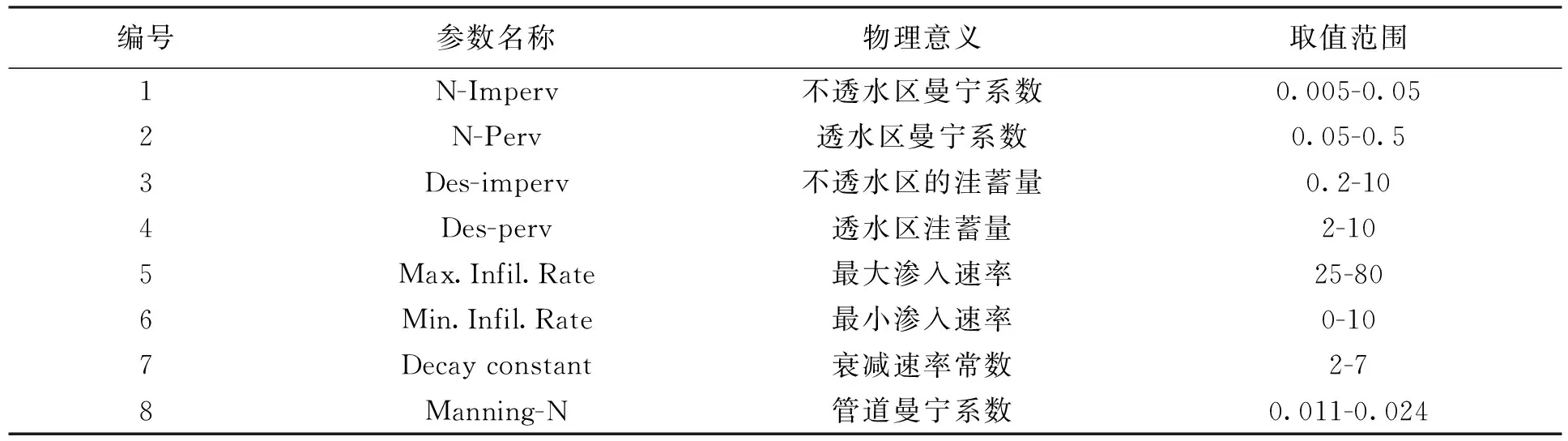
表1 SWMM模型参数取值范围
1.3.2 目标函数
根据模型所涉及到的主要产汇流参数,将能表征径流特征的峰值流量和总产流两项提出,并结合水文相关规范,最终确定目标函数选择为峰值流量绝对百分比误差和总产流的平衡误差系数,其具体的计算方法如下表所示:
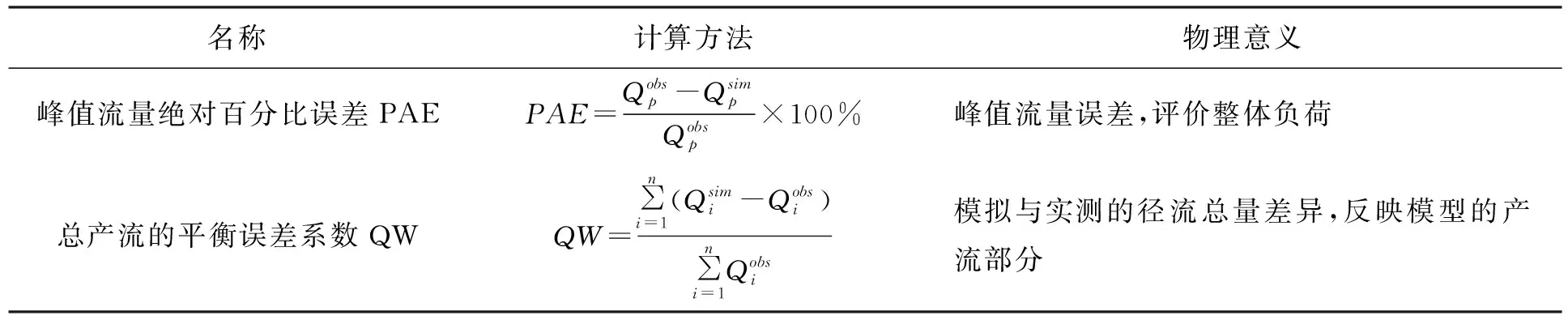
表2 目标函数
1.4 参数敏感性分析方法
1.4.1 Morris法
Morris筛选法是由Max D.Morris首次在1991年提出的,它作为局部敏感性分析方法关注单个参数对于模型模拟效果的影响,操作性强、简单快捷、被广泛应用[15].Morris筛选法主要思想是改变单一变量参数xi而其他参数不变后,在参数允许的阈值内随机改变xi取值,通过其对于输出值的影响来判断参数敏感性的一种方法[16].本次研究以10%为固定步长对于各个水文水力参数进行扰动,取值分别为±10%、±20%、±30%.在保证某一参数变化时控制其他参数不变,探究单一参数对于目标值的影响,选取目标值为总产流和峰值流量两项重要表征项相关形式,具体式如下:
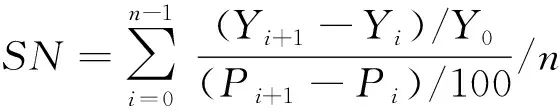
(1)
其中:SN:敏感性判别因子;Yi:模型第i次运行输出值;Yi+1:模型第i次运行输出值;Y0:参数调整后的计算结果初始值;Pi:第i次模型运行参数值相对于校准后参数值的变化百分率;Pi+1:第i+1次模型运行参数值相对于校准后参数值的变化百分率.
1.4.2 Sobol法
基于蒙特卡罗法的Sobol法是一种定量全局敏感度分析方法,它能够求解高度非线性模型中的参数间的相互作用所产生的灵敏度[17].它主要是利用了目标函数的方差可以分解为单个参数的方差和各个参数之间相互作用的方差的思想,来表征各个参数的独立或相互关系灵敏度.Sobol法中,假设模型的函数形式为y=f(x),其中参数x可以由xi(i=1,2,…,n)的n维离散表示.若f(x)本身可积,xi服从[0,1]上的均匀分布,则f(x)可以表示为:
(2)
式中共2n项相加和,将其写作方差的形式,利用D表示,并且归一化则可以得到如下公式:
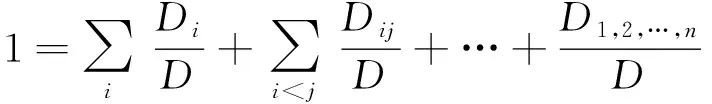
(3)
式中各项即为一阶、二阶、总阶灵敏度表达式:

(4)
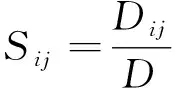
(5)

(6)
式中:Si表征xi单独作用时对于输出项的灵敏度值,Sij表征xi和xj两个参数共同作用时对于输出项的灵敏度值,STi表征有xi参与的所有项对于输出项的灵敏度值.
2 结果与分析
2.1 局部敏感度分析
利用修正Morris筛选法对研究区子汇水区以固定步长进行扰动,根据目标函数对各个参数的敏感度进行排序,结果表3所示:
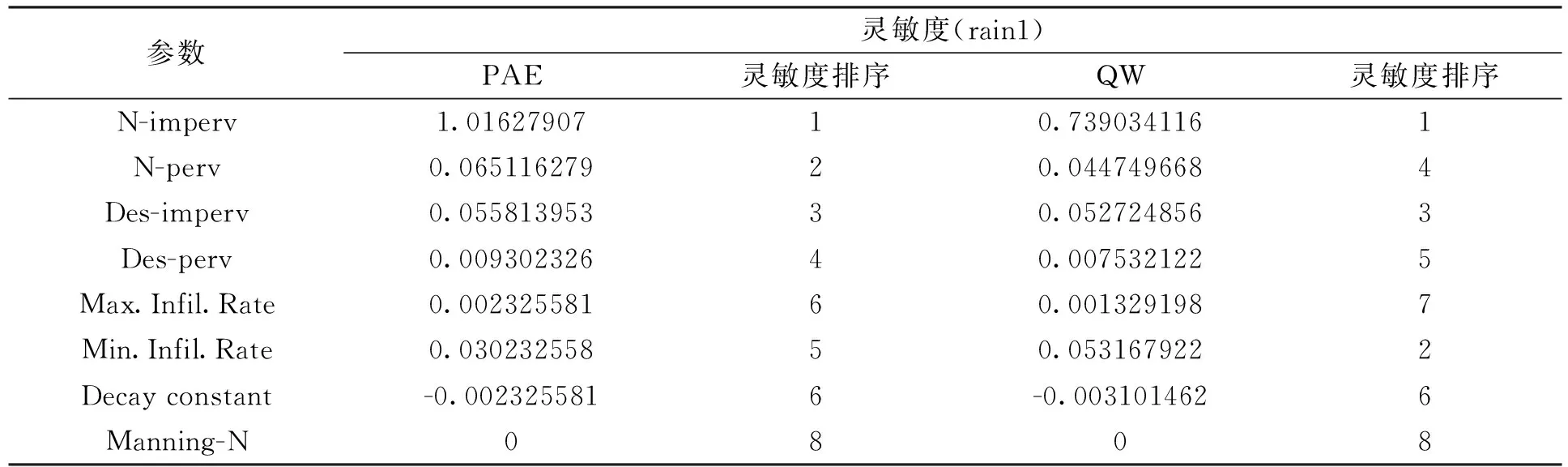
表3 局部灵敏度结果排序
通过分析得知,对于峰值流量而言,敏感参数中敏感度大小依次为N-imperv、N-perv和Des-imperv,其中N-imperv为高敏感参数.对于总产流而言,敏感参数则依照敏感度大小为N-imperv、Min.Infil.Rate和Des-imperv.对于此两项目标函数,剩余参数均为不敏感参数.
以峰值流量的绝对百分比误差为目标函数时,N-imperv的敏感程度最高,这是因为研究区不透水区面积相对更广,与不透水区径流相关参数(N-imperv和Des-imperv)对于模型的产流过程取重要作用,相关的参数敏感程度高.对于总产流平衡误差系数为目标函数时,由于下垫面的透水情况所造成的产流量的影响尤为明显.本次采用的输入降雨时间序列为20年一遇的实测点降雨数据,降雨强度较大的情况下,土壤中的含水量迅速增加,与下渗有关的参数敏感性相对较强.
两目标函数下的敏感参数对比可知,N-imperv的敏感度排序未发生变化,但是其敏感度却由高敏感参数变为敏感参数,敏感度水平有所下降.Min.Infil.Rate和Des-imperv为敏感参数,其余参数项为不敏感参数.Min.Infil.Rate由不敏感参数转变为敏感参数,敏感度有所上升.这表明同一参数在输出结果不同时,它的敏感性也会表现出差异.
2.2 全局敏感度分析
本次研究的主要研究参数共8项,按照Sobol法步骤进行计算,利用拉丁超立方抽样,抽取3000个基础样本,共2组,分别用矩阵A、B表示,将B矩阵的每一列替换为A矩阵中的每一列,组成新的矩阵,与原来A、B矩阵共同构成(8+2)组样本数矩阵.将得到的10组共30000个数据样本带入到SWMM模型中进行模拟,输出共30000组状态报告文件,按照要求提取相应的输出值,将其进行处理后作为目标函数,对其进行敏感度分析.
本文中主要求解模型的一阶敏感度和总阶敏感度,探究参数单独作用时和与其他参数共同作用时对于目标函数的敏感度的影响.交互敏感度的计算方法为一阶敏感度与总阶敏感度差值,用以表示模型某一参数与其他参数的相互作用.
根据计算结果,将参数对应于两个目标函数的一阶灵敏度(Si)、总阶灵敏度(STi)与交互敏感度(STi-Si)汇总到表4和表5中.选用0.01作为敏感度的阈值,及敏感度值在0.01及以上,表示敏感参数,否则为敏感参数.
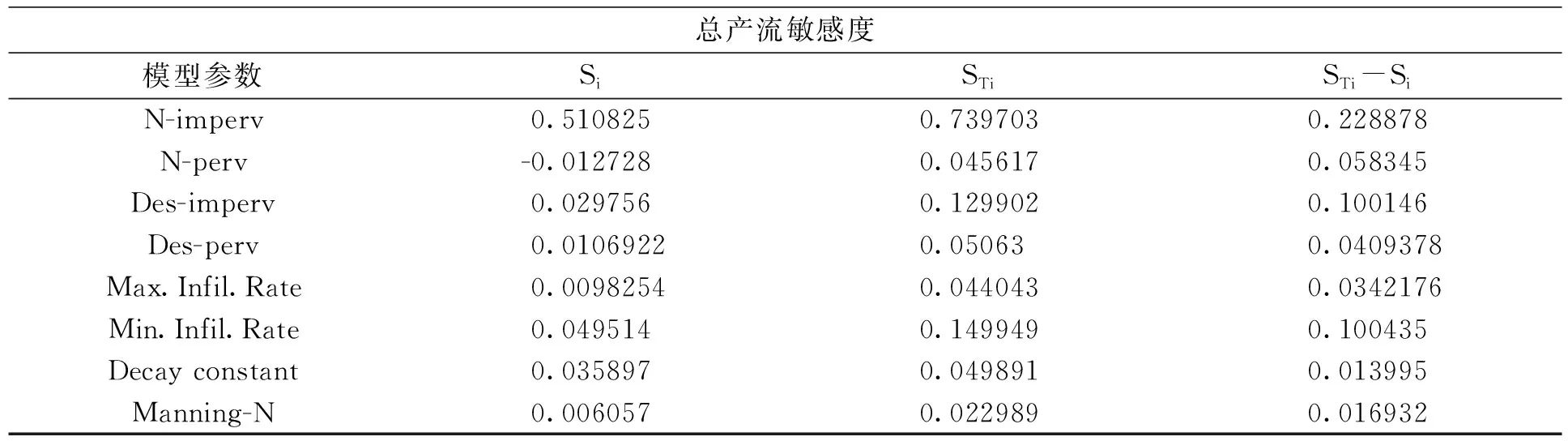
表4 关于总产流的全局灵敏度结果分析
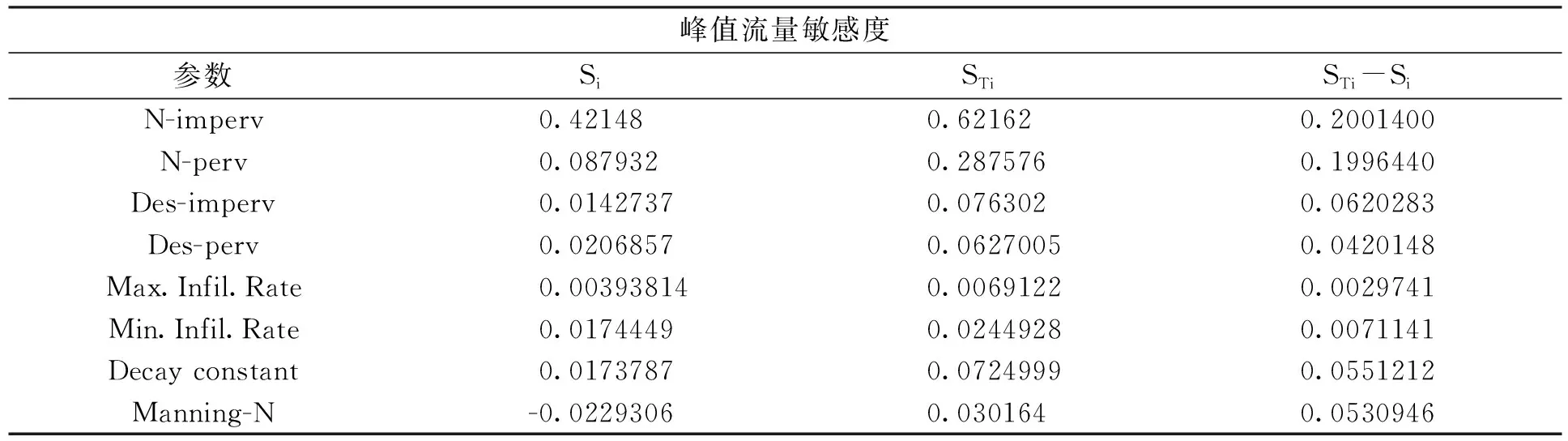
表5 关于峰值流量的全局灵敏度结果分析
对于总产流的一阶敏感度而言,敏感参数排序由大至小依次为N-imperv、Min.Infil.Rate、Des-imperv、Des-perv,与局部敏感度分析相同,强降雨Rain1条件下,与下渗有关的参数Decay constant、Min.Infil.Rate为敏感参数,Max.Infil.Rate值同样受影响,敏感程度上升.对于峰值流量的一阶敏感度而言,敏感参数排序由大至小依次为N-imperv、N-perv、Des-perv、Min.Infil.Rate、Des-imperv、Decay constant.
对于总产流而言,一阶敏感度中N-imperv的敏感性与其他参数相比较明显要大,这说明N-imperv参数对于研究区域的总产流而言是十分重要的参数项,地表径流受人类活动与下垫面影响较大.对于峰值流量的一阶敏感度而言,除了N-imperv之外,N-perv的敏感度排序较高,这说明研究区的不透水区面积较大,但是透水区在对于峰值流量的影响仍然起了很大作用.
交互敏感度是总阶敏感度与一阶敏感度的差值,可以表征参数之间的耦合性.N-imperv、Min.Infil.Rate、N-perv、Des-perv的交互敏感度在10%左右,其值表示此独立参数与其他参数的耦合性强.Des-perv和Decay constant的值相对较小,其表现出的与其他参数的耦合性更差一些,受到其他参数的影响较小,属于相对独立的参数.
2.3 对比分析
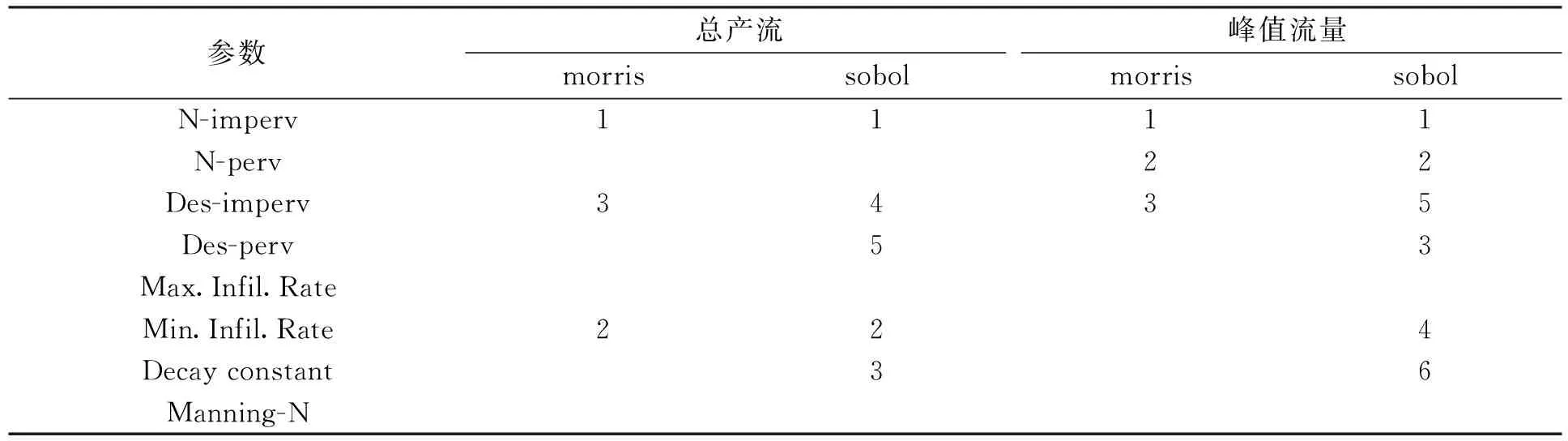
表6 全局与局部灵敏度排序汇总
由此表可以看出,修正Morris筛选法作为局部敏感度分析法,对两项目标函数的敏感度分析中,分别有三项参数被识别为敏感参数,其余为不敏感参数.而Sobol法进行敏感度分析时,对于两项目标函数的敏感参数项包括但是不仅限于原本的三项,而是有更多的敏感参数项被识别出来.由此可见,修正Morris筛选法对于参数的敏感性分析具有一定的借鉴意义,但是其对于模型总体敏感参数的识别并不突出,许多敏感参数被识别为不敏感参数.在分析敏感度时,需要综合考虑,不能作为直接依据.
3 结 论
(1)根据研究区情况,利用局部Morris筛选法时,共筛选出N-imperv、N-perv、Des-imperv和Min.Infil.Rate 4项敏感参数,这些与地表径流和下渗相关参数表现出的敏感性与所选目标函数相关.利用全局Sobol法时,除去以上4项,同时将Des-perv和Decay constant判别为敏感参数.两种方法产生差异的原因主要是由于前者关注单个参数的影响,而后者则关注参数对整体的影响.Des-perv和Decay constant单独作用时,对于研究区的两项目标函数的影响较小,但在与其他参数共同作用时,对其他参数产生影响较大,间接影响最终结果,被标识为敏感参数.
(2)局部修正Morris筛选法对于对于敏感参数项有一定的识别作用,全局Sobol法所需基础参数大,通过对于参数进行敏感性分析,认为局部敏感性分析方法具有一定的参考性,但是却会对于一些在全局敏感参数项识别有误,因此在进行敏感性分析的时候,应当全局与局部敏感分析综合考虑.同时,敏感性分析时并未考虑降雨强度这一因素对于参数敏感性的影响,在今后的研究中,应当加强此方面分析,为模型优化提供更可行精确的研究方法.
