空调房间侧送风非等温射流分形特性实验研究
2021-08-10冯仁杰赵延博
冯仁杰 高 天 张 雄 赵延博
(河北建筑工程学院,河北 张家口 075000)
0 引 言
在现有的侧送风气流组织设计当中,风口轴心射流速度与侧送风射流射程及风口当量直径三者之间不是完全匹配的,存在一定的误差.究其原因,是由于射流在风口处就已紊乱化,形成湍流运动,湍流速度在时间序列上是波动且无序的,并不是一个定值,而原有方法用射流速度时均值代替瞬时值进行气流组织设计,无法反映流场实际情况,导致设计误差的产生.这种误差有可能导致侧送风射流无法到达室内预定区域便提前进入室内工作区,影响到工作区人员的舒适度.正因为这样,往常空调设计都需要反复校核房间侧送风气流组织设计参数是否满足房间要求,工作比较繁琐,给空调房间侧送风气流组织设计造成了一定的困难.
本文采用理论推导与实验验证相结合的方式,将分形的概念引入到空调房间流场特性的研究中,探究运用分形理论研究侧送风气流组织的可行性,为空调房间侧送风气流组织研究提供一种新的思路和方向.
1 实验内容及方案设计
1.1 实验台的搭建
本实验在河北建筑工程学院的通风空调一号综合实验室中进行.实验室中有一间密闭的实验房间,该实验房间长6 m,宽5 m,高2.8 m,四周均为保温墙,门窗密封性完好,保证了室内温度场的稳定性.其内布置有侧送风气流组织实验台,该实验台由吊顶式新风机组,通风管道,侧送风口,回风口等设备及构件组成.其中,吊顶式新风机组型号为XSQ-1000D,额定功率为0.2W/380V,风量为1000m3/h,制冷量为12.15kW,制热量为22.14kW,如图1所示;机组连接着一段通风管道,位于房间一侧,管道末端安装有一个方形双层百叶侧送风口,其当量直径为0.26m,如图2所示.侧送风口距地面1.8m,距屋顶1m,侧面距近端墙体2m,在侧面墙体不会干扰到空气流场的前提下,确保侧送风射流沿送风方向自由流动,保证实验条件满足实验的要求.

图1 吊顶式新风机组 图2 侧送风口 图3 变频器
在风机控制箱电源处接有变频器,如图3所示.变频器靠内部IGBT的开断来调整输出电源的电压和频率,根据风机的实际需要来提供其所需要的电源电压,达到风机变频调节的目的.继而通过变频调节的方式对侧送风风速进行调节,以获取不同工况下侧送风射流出口处的轴心速度和轴心温差数据(需要强调的是,此处轴心速度数据和轴心温差数据为瞬时速度时间序列数据组和瞬时温差时间序列数据组).
1.2 实验测点布置及方法
本次实验需要采集侧送风口出口瞬时风速及瞬时温差,因此须在侧送风口射流出口处的轴心线上进行测点的布置.瞬时速度时间序列数据和瞬时温差时间序列数据采集使用多点风速仪(图4)和温度自记仪(图5)进行记录.需要注意的是,多点风速仪使用1个风速探头(图6)对射流出口处射流轴心速度记录即可;而温度自记仪需使用5个探头,其中1个对射流出口处射流轴心温度进行记录,还有2个需对射流出口处射流轴心周围温度进行记录,最后2个对室内温度进行记录,为实验提供容错率,避免轴心温差误差过大.需要强调的是,6个探头须同时工作,同时记录,保证数据的在时间序列上的一致性.

图4 多点式风速仪 图5 温度自记仪及探头 图6 风速探头
在实验中,每0.1s记录一组数据,每次实验记录1000组数据.为了数据的稳定性和可靠性,同种工况进行5-10次实验,完成后对同种工况下的实验数据进行对比分析,剔除掉误差较大的数据.本次实验共记录了15种工况下(图7)的瞬时速度时间序列数据组和瞬时温差时间序列数据组.其中,风速数据的统一单位为m/s,温度数据的统一单位为℃,下文中所有表格中数据的单位均以此为准.

工况样本号123456789101112131415平均风速8.157.767.387.046.656.335.965.575.174.744.263.783.292.712.21
2 分形维数与湍流强度的关系研究
2.1 分形维数的计算
分形维数也叫分数维数,是描述自然界中不规则形体复杂程度的一个定量指标.本文中将采用盒计数维数法对侧送风射流的分形维数进行计算,盒计数维数又称为闵可夫斯基(Minkowski)维数、容量维数和度量维数.是测定分形生长、特别是二维随机生长图形的分形维数一种常用方法.随机分形现象在自然界中大量存在,所以这种应用方法具有普遍性,而且这种维数由于计算简单和易于经验估计,得到了分形理论应用研究者的广泛青睐.但该方法同时也存在一定的缺陷,其并不能反映计算对象的不均匀性,因此会存在计算误差.盒计数维数法一般适用于计算只有单一对象的分形维数.
盒计数维数的定义[1]如下:
设F是Rn空间的任意非空有界子集,r表示用来覆盖测量对象的盒子的边长,对于任意的一个r>0,N(r)表示用来覆盖F所需要的盒子数.如果存在D,使得r→0时,有
N(F)∝1/rD
(1)
那么称D为F的盒计数维数(盒维数).盒维数为D,当且仅当存在一个整数k使得
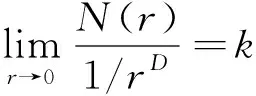
(2)
对上述方程(2)两边取对数,得:
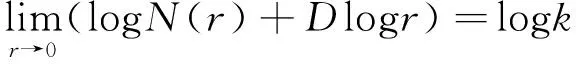
(3)
进一步求得:
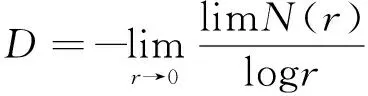
(4)
前文提到本实验各工况下侧送风口射流出口处的轴心瞬时风速由多点式风速仪测得,每0.1s记录一组数据,每种工况下记录1000组数据.以样本号1的数据记录结果为例,其瞬时风速在时间序列上的数据如图8所示.
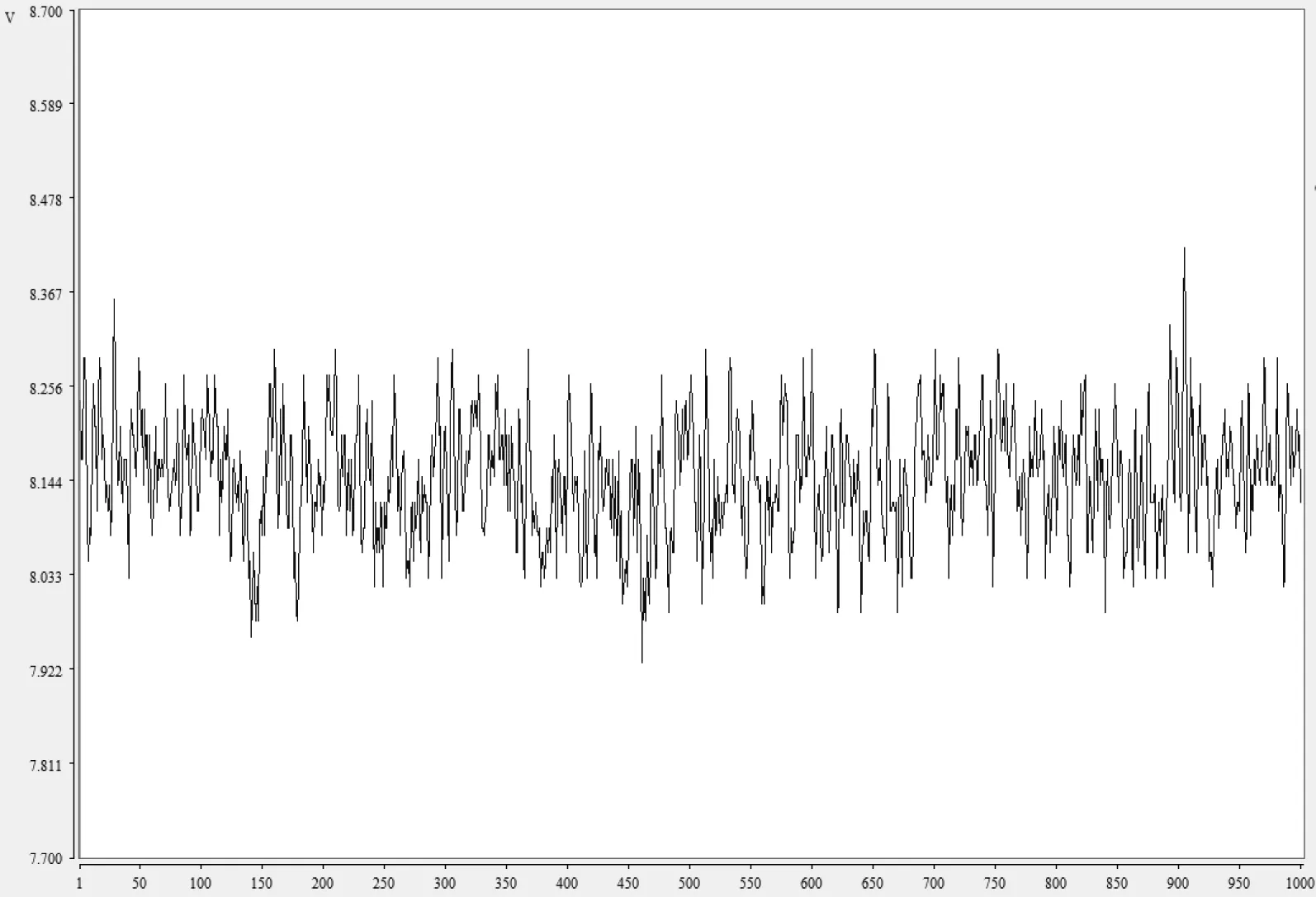
图8 平均风速为8.15m/s时的速度时间序列图
根据计算盒计数维数的步骤,编写相对应的MATLAB程序,并将数据带入MATLAB程序中,对样本号1的分形维数进行计算,如图9所示.
图9 平均风速为8.15m/s时速度时间序列的分形维数
依据以上步骤,分别对样本号2—15的分形维数进行计算,结果如图10所示.

图10 各工况下的分形维数
2.2 湍流强度的计算
假设在本文的实验中各工况下的采样次数为n,得到的周期t内速度时间序列的平均速度为:
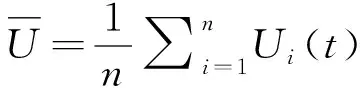
(5)
脉动速度的均方根为:
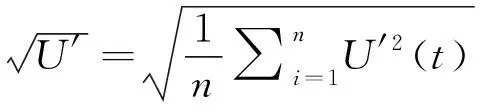
(6)
所以湍流强度为:
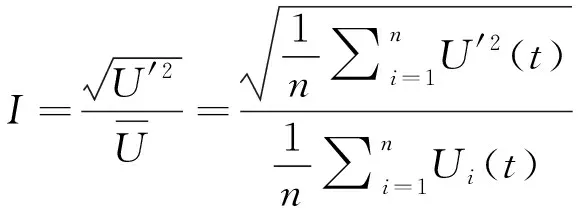
(7)
根据以上湍流强度的计算步骤,带入在实验中所得的瞬时风速数据,对各工况下侧送风口射流出口处轴心射流的湍流强度进行计算,结果如图11所示.

图11 各工况下的湍流强度
2.3 分形维数与湍流强度的关系
在2.1和2.2中计算出的分形维数和湍流强度的数据的基础上,利用Origin软件对侧送风气流组织下侧送风口射流出口处轴心射流的分形维数和湍流强度进行拟合分析,结果如图12所示.
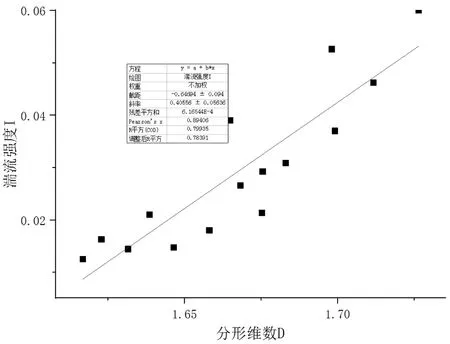
图12 侧送风气流组织下分形维数与湍流强度的回归分析图
从上图中可以直观地看到湍流强度I随分形维数D的变化关系,湍流强度随着分形维数的增加而增加,呈正相关性,并且是明显的线性关系,即分形维数可以表征侧送风射流湍流强度的大小.利用回归分析拟合得到的湍流强度I和分形维数D的数学模型如下:
I=0.4056D-0.6469
(8)
通过拟合得到的分形维数和湍流强度的函数关系式可以直观地看出它们之间的定量变化关系.
3 分形维数与阿基米德准数的关系研究
3.1 阿基米德准数的计算
阿基米德准数是一个评价室内气流组织的特性数值.阿基米德准数的计算公式[2]如下:
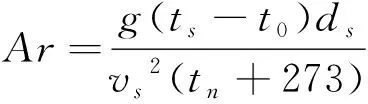
(9)
式中:g—重力加速度,m/s2
ts—射流出口温度,℃
t0—射流周围空气温度,℃
ds—送风口当量直径,m
vs—射流出口速度,m/s
tn—射流周围空气温度,℃
根据以上阿基米德准数的计算步骤,带入在实验中所得的瞬时风速及瞬时温度数据,对各工况下侧送风口射流的阿基米德准数进行计算,结果如图13所示.
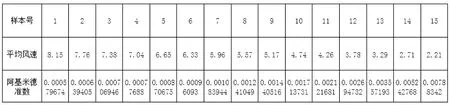
图13 各工况下的阿基米德准数
3.2 湍流强度与阿基米德准数的关系
在空调房间侧送风气流组织研究中发现,侧送风射流与室内气流之间存在温度差和密度差,导致侧送风射流与室内气流混合而产生湍流,在能量耗散的过程中,轴心射流因惯性力逐渐无法克服浮升力做功,导致冷射流方向向重力方向发生偏转.湍流强度是衡量湍流强弱的相对指标,而阿基米德准数是轴心射流偏转程度的评价指标,二者都是因湍流现象而产生的特性数值,具有共性联系.
在2.2和3.1中计算出的湍流强度和阿基米德准数的数据的基础上,利用Origin软件对侧送风气流组织下侧送风口射流出口处轴心射流的湍流强度和阿基米德准数进行拟合分析,结果如图14所示.
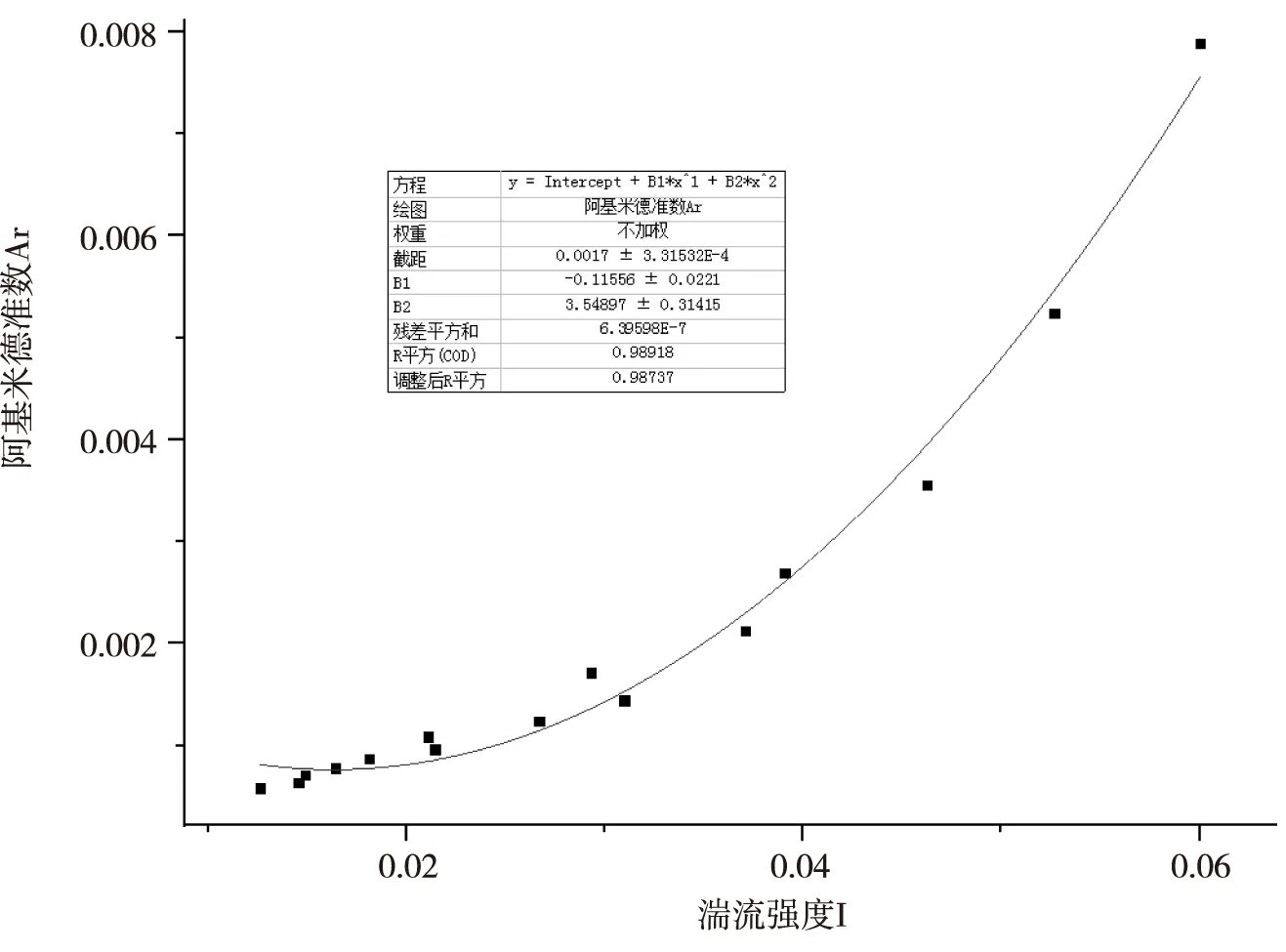
图14 侧送风气流组织下湍流强度与阿基米德准数的回归分析图
从上图中可以直观地看到阿基米德准数Ar随湍流强度I的变化关系,阿基米德准数随着湍流强度的增加而增加,呈正相关性,并呈偶次幂函数关系.利用回归分析拟合得到的阿基米德准数Ar和湍流强度I的数学模型如下:
Ar=3.549I2-0.1156I+0.0017
(10)
在以上研究的基础上,将利用回归分析拟合得到的湍流强度I和分形维数D的数学模型以及阿基米德准数Ar和湍流强度I的数学模型进行联立推导,可得到阿基米德准数Ar和分形维数D的函数关系式,如下所示:
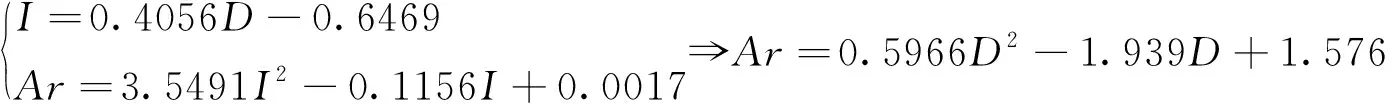
(11)
在以上研究当中发现,分形维数越大,侧送风射流的湍流强度也就越大,导致空气流场的紊乱程度随之增强,阿基米德准数也随之更大,而阿基米德准数便是评价室内气流组织的特性数值之一.在以上研究结论的基础上,便可以将分形维数与侧送风气流组织设计联系到一起,使分形维数这一能够定量反映侧送风射流运动的复杂性和不规则程度的特性数值成为一个新的侧送风气流组织设计参数.
4 结 语
本文所涉及研究通过测量空调房间侧送风口处送风射流的瞬时速度及瞬时温差,得到侧送风射流在时间序列上的分形维数,湍流强度以及阿基米德准数,通过对数据的分析发现,空调房间侧送风射流风口处的湍流强度随着分形维数的增大而增大,并呈明显的线性关系;而阿基米德准数随着湍流强度的增大而增大,并呈偶次幂函数关系.在此基础上引入分形维数这一能够定量反映侧送风射流运动的复杂性和不规则程度的特性数值成为一个新的侧送风气流组织设计参数,以评价湍流运动对于侧送风气流组织设计的影响,为以后的侧送风气流组织研究提供一个新的方向.
本文中的实验由于场地及条件限制,仅涉及到实验对象为方形双层百叶侧送风口,上送下回这一种形式,本文中所得拟合公式在其他侧送风形式下是否适用,还需进一步验证.
