基于响应面法的柱塞泵迷宫密封优化设计

杨煜兵，张春光，刘光恒，李上青，张俊峰，安 磊，褚 帅

（沈阳仪表科学研究院有限公司 研究开发部，沈阳 110043）

0 引言

超高压往复式柱塞泵广泛用于水力破拆系统、水刀切割、农业灌溉等领域，在超高压范围内，填料式密封失效，因此大多采用迷宫密封方式。迷宫密封中，影响密封效果即泄漏量的因素有很多，包括密封入口压力、密封间隙、迷宫密封槽数量、密封槽尺寸（如角度、间距等）等［1-2］。对迷宫密封结构进行优化，降低迷宫密封的泄漏量，是往复式柱塞泵设计的重要环节。使用计算流体动力学（CFD）方法对迷宫密封结构进行优化计算，需要根据计算结果反复修改迷宫密封结构，优化计算极为耗时，而且该方法不易获得全局最优解［3］。遗传算法（Genetic Algorithm，GA）是一种不需要具体函数形式的非数值优化算法， 可以寻得全局最优解，适合于离散变量的优化问题。但遗传算法优化过程中需要大量的数值计算，优化效率低［4］。而响应面法（Response Surface Methodology，RSM）使用试验设计（Design of Experiment，DOE）方法对参数设计点集合进行试验（仿真试验），从而得到优化目标和约束的响应面模型，可以替代CFD的反复仿真计算，计算效率得到提高［5-7］。本文以某型号的往复式柱塞泵迷宫密封系统为对象，对迷宫密封进行了参数化建模，采用神经网络响应面模型，并应用遗传算法进行优化计算，得到了设计空间范围内的全局最优解。通过优化计算，能有效降低迷宫密封系统的泄漏量。

1 迷宫密封优化模型

本文研究的迷宫密封系统位于超高压柱塞泵的液力端，如图1（a）所示。柱塞向左侧进程时，在铜套内部产生高压水，铜套与柱塞之间留有极小的间隙，在铜套上开出迷宫密封槽，高压水通过这些迷宫密封槽时，会消耗压力势能，达到减少泄漏的目的。迷宫密封参数化结构示意图如图1（b）所示。A、B代表密封槽角度，H为密封槽高度，L为2个槽间距，W为密封槽顶部宽度，G为铜套与柱塞间隙，共计6个参数。

图1 柱塞泵迷宫密封系统结构Fig.1 The structure of piston pump labyrinth seal system

1.1 迷宫密封的设计参数

本次优化设计采用的迷宫密封设计参数的初始尺寸及各参数设计空间见表1。

表1 迷宫密封结构原型尺寸及结构参数设计空间Tab.1 Labyrinth seal structure original size and design space of each parameter

1.2 CFD计算模型

为计算迷宫密封密封泄漏量，本文对对迷宫密封系统的流场进行了CFD分析。CFD计算的几何模型选取迷宫密封的原型结构，该迷宫密封系统总长100 mm，密封沟槽数目为20个。划分的网格经过网格无关性验证，确定了最终CFD计算使用的的网格数目为55.8万。计算使用的部分网格如图2所示。

图2 宫密封密封CFD计算网格（仅展示部分网格）Fig.2 The grids for CFD calculation of labyrinth seal(Only part of the grids is shown)

迷宫密封内的介质流动可以认为是稳态的湍流流动，CFD计算采用的湍流模型为SST k-omega模型。工作介质为纯水，其密度为998 kg/m3，动力粘度为0.001 003 Pa·s，工作温度为25 ℃。计算的边界条件及设置见表2。

表2 边界条件及设置Tab.2 Configuration of boundary conditions

为了验证CFD计算结果，将CFD计算的迷宫密封泄漏量与理论计算公式进行了对比。迷宫密封泄漏量理论计算计算公式［8］：

式中 Qm——泄漏量，kg/s；

α —— 流量系数，工程上流量系数一般取0.6～0.8，本文取 0.7；

A ——密封间隙面积，m2；

p0——入口压力，MPa；

ρ0——入口介质密度，kg/m；

g ——重力加速度，m/s2， g=9.81 m/s2。

入口压力从80 MPa到160 MPa变化。CFD计算结果与理论计算结果如图2所示。

由图3可知，CFD计算结果与式（1）计算结果趋势一致，误差为1.6%，说明本文使用的CFD模型是准确可靠的。

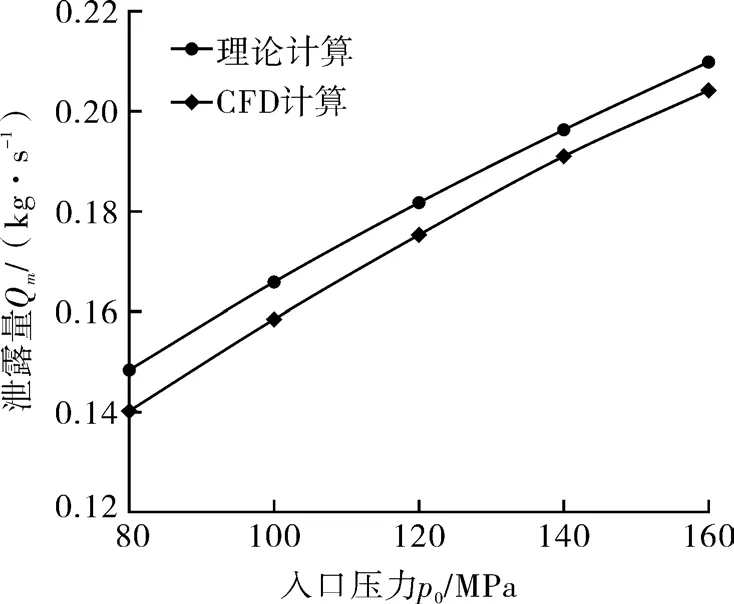
图3 CFD计算结果与理论计算结果对比Fig.3 Comparison of CFD results and theoretical calculation results

2 神经网络响应面模型

2.1 试验设计和神经网络响应面

在构造响应面模型之前，应进行试验设计（Design of Experiment，DOE）。试验设计通过合理选择样本点的数量和样本点在设计区间内的分布，制定CFD仿真方案。拉丁超立方（Latin Hypercube Design，LHD）试验设计是由MCKAY等提出的一种试验设计方法，该方法具有有效的空间填充能力，而且一个设计参数的每个水平只被研究一次［9-10］。（本文根据表1所示的设计参数和以泄漏量为输出参量，采用拉丁超立方法得到的试验设计结果见表3。

表3 拉丁超立方试验设计结果Tab.3 The result of LHD DOE

样本点的输出参数泄漏量采用CFD方法计算。响应面法基于试验设计和数理统计理论，其依靠目标函数本身的性质确定最优解，适合处理非线性数据。传统的响应面采用二次多项式函数形式，通过试验样本解出出多项式系数，只能构建二次近似模型。而神经网络响应面属于多层前馈网络，包含有输入层、隐含层和输出层，同层单元之间互不相连［11-17］。神经网络模型示意如图4所示。

图4 神经网络示意Fig.4 Schematic diagram of neural network

本次研究采用了多输入、单隐含层和单输出的三层神经网络模型构建了响应面模型。为了对响应面准确度进行检验，采用决定系数（R2）和均方根误差（Root Mean Square Error，RMSE）作为验证准则［18］，其定义如下：

N ——检验样本点数目。

R2愈接近1、RMSE愈小，响应面的拟合程度越好。在试验设计点的间隔中，增加数个新点作为检验样本点，本文通过对30组检验样本点的计算得到：R2=0.999 11，RMSE=0.007 049 kg/s，说明神经网络响应面模型的拟合精度较高，满足优化需求。

图5示出了迷宫密封泄漏量与各设计参数的响应面模型。

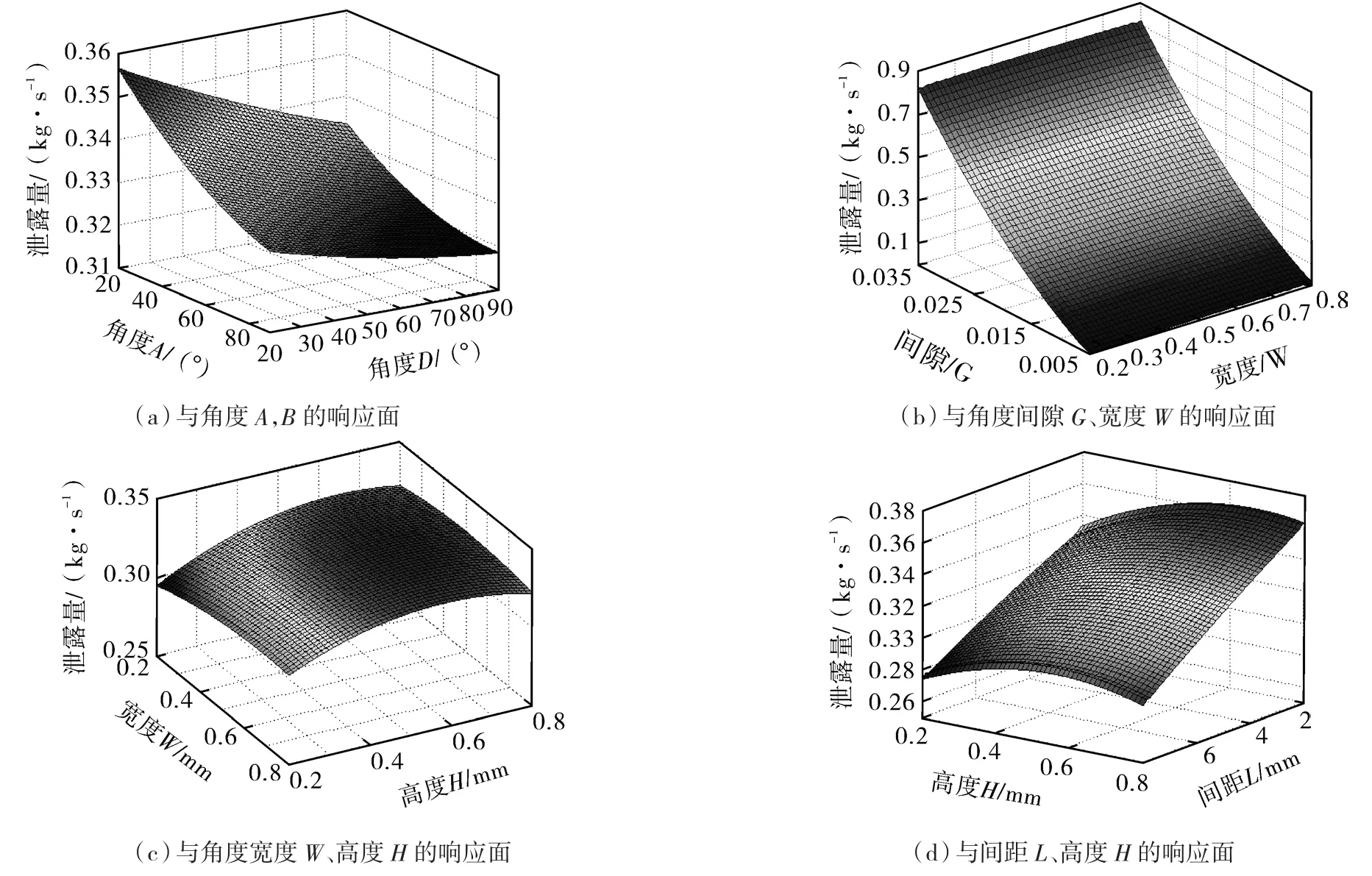
图5 泄漏量与各设计参数的响应面Fig.5 The response surface of leakage to each design parameter

由图5可知，迷宫密封泄漏量的影响因素中间隙G的影响最大；角度A比角度B的影响大；迷宫密封槽的高度与宽度对泄漏量影响较小，相比之下，密封槽间距对泄漏量影响较大。各参数对泄漏量的敏感度见表4。

表4 各参数对泄漏量敏感度Tab.4 Pie chart of sensitivity of each parameter to leakage

2.2 基于遗传算法的优化计算

遗传算法（Genetic Algorithm，GA）通过对生物自然选择和进化的模拟进行随机搜索，并且不需要具体的函数形式就可以获得全局最优解。其核心思想是：通过初代种群的的复制、交叉和变异来产生下一代种群［19-24］。本文采用的遗传优化算法的流程如图6所示。遗传算法需设置的主要参数有种群数量、种群代数、变异概率、交叉概率及收敛准则。种群数量对遗传算法的性能影响较大，种群数量太小容易产生较大的采样误差，太大的种群数量会占用大量的计算资源；种群代数即迭代次数，目前其取值主要依靠经验或试验；变异概率用来控制种群中发生变异行为的个体的数量，从而使种群保持一定的多样性，取值范围在0～0.5之间，变异概率过大，会对解产生比较大的破化性，而且容易丢失掉最优解，变异概率太小，会使算法收敛速度变慢；交叉概率用来控制种群中发生交叉行为（2个父代个体的部分结构加以替换重组而生成新个体）的个体的数量，取值范围在 0～1之间［25］。

图6 遗传算法优化流程Fig.6 Flow chart of genetic algorithm optimization

综合考虑本文研究的迷宫密封结构的实际工程情况，遗传算法主要参数设置见表5。

表5 遗传算法主要参数设置Tab.5 Configuration of main parameters of genetic algorithm

3 优化结果

本文针对迷宫密封结构的6个参数为设计变量，以泄漏量最小为优化目标，经过试验设计，建立了神经网络响应面模型，应用遗传算法对迷宫密封结构进行了优化计算，并对优化后的迷宫密封结构进行了CFD计算验证。优化结果及CFD验证结果见表6。

表6 优化结果及CFD验证Tab.6 The result of optimization and its CFD verification

由表6可知，基于响应面的优化结果与CFD验证结果误差为4.32%，说明响应面模型具有良好的准确可靠性。通过优化计算，迷宫密封的泄漏量由原型的0.197 9 kg/s降至了0.006 012 kg/s，极大改善了密封性能。

4 结语

针对某型超高压往复式柱塞泵，本文提出了一种CFD方法、响应面模型和遗传算法相结合的迷宫密封结构优化设计方法。通过对响应面模型的分析，可知影响迷宫密封系统的泄漏量的因素中间隙的比重最大，其次是密封槽角度、间距、宽度和高度。优化后的迷宫密封系统的泄漏量降幅极大，提高了迷宫密封的可靠性。将优化结果与CFD计算结进行了比较，表明优化模型具有较高精度，可以为超高压柱塞泵迷宫密封系统的设计优化提供可靠的参考。