欠驱动自主水下航行器航迹追踪控制

陈 伟,芦 海,杨 雯,吴青帅,冷建兴*

(1.浙江大学 海洋学院，舟山 316021)(2.海南联网二回项目管理有限公司,海口 570100)(3.中国南方电网超高压输电公司,海口 570206)

自主水下航行器作为高技术海洋工程装备在大海作业中应用广泛，不仅可以在深海海底进行海洋观察和资源探测，也可用于近海巡查海底电缆和维护石油管道.自主水下航行器的发展具有广泛的研究意义，发展前景广阔美好，如今依然存在一些挑战.水下航行器要想实现无人无线远距离自主航行，对于控制策略有着极高的要求，尤其应该注意它在海中运行时候具有模型非线性、高耦合、海洋环境随时间变化、波浪海流干扰不确定性等特点[1-2].

航迹控制需要水下航行器追踪一条随时间变化预先设计好的航行轨迹，必要情况下需要对起始和到达时候的速度有所要求.对于水下航行器的常见控制方法有PID控制、滑模控制、反步控制和模糊控制等，文献[3]通过实验和仿真的办法对几种常见控制策略进行比较，并且提出一种改进型滑模控制器.水下航行器面对的外界干扰难以准确实时测量，文献[4]基于扩展型观测器和高阶滑模控制提出一种自适应干扰观测器，有效应对时变不确定性干扰.文献[5]考虑到墙壁等边界对航行器的干扰，提出一种慢速时变干扰观测器.文献[6]考虑到位置约束，并对欠驱动航行器设计一个主动反步法控制器抑制干扰影响.文献[7]提出了一种有限时间观察器，能有效解决模型中部分动力未知的困难.为了对动力学不确定参数和外界干扰起到自适应补偿的效果，文献[8]设计一种滑模自适应控制器，文献[9]结合视线法设计非线性干扰观测器,文献[10]设计一种双回路积分滑模控制器.文献[11]在反步法和滑模控制的基础上，通过降维扩展型状态观测器对外部扰动做出补偿，也考虑到输入的有界性.文献[12]基于导航误差设计了一种鲁棒性较强的模糊自适应控制器，可以兼顾执行器存在饱和现象的限制条件.文献[13]在反步法控制器的基础上考虑到水下航行器在全驱动和欠驱动系统之间平滑切换的调节过程.文献[14]设计了终端滑模控制方案，最后在关联扰动下表现出良好的稳定性和鲁棒性.文献[15]针对欠驱动水下航行器系统设计了一个自适应快速非奇异终端滑模控制方案.文献[16]基于反步法控制和仿生速度准则将实际航行器速度变化变得更为平滑.文献[17]在反步滑模控制基础上，使用模糊控制的算法获得滑模增益系数，最终取得良好的鲁棒性.文献[18]利用基于李亚普诺夫模型的在线预测系统有效提高了控制器的表现性能.

文中研究的水下航行器属于欠驱动控制系统，主要对二维平面内三自由度系统航迹控制进行探讨.针对其中运动学和动力学间的各自由度状态量相互耦合情况，对耦合项进行建立数学模型，并以此为控制建模基础；针对航行器控制过程中需要考虑的坐标系、模型参数和系统状态量进行定义和模型确定；针对控制系统的设计思路、控制方程的确切形式和系统稳定性的理论验证；针对控制系统进行仿真，探究其控制性能并验证理论推导.

1 航行器模型

航行器总共拥有6个自由度，包含x、y、z3个平动自由度和ζx、ζy、ζz3个旋转自由度.但文中主要考虑航行器在平面运动过程中的二维路径跟踪控制，也就是x、y、ζz3个自由度.一般来说，水下航行器装备尾部螺旋桨或喷水装置作为船身方向驱动器，通过尾鳍等装置作为船体平面内旋转驱动器.两个驱动器却要用来控制平面内3个自由度，也就导致了欠驱动的难题.

在模型建立之前，先通过图1介绍文中采用的3个坐标系{e}、{b}、{d}.大地坐标系{e}是惯性坐标系，坐标系原点是Oe，坐标轴分别是xyz；航行器实际运动坐标系{b}随船体本身运动，坐标原点为船体重心Ob,坐标轴为ubwb；理想状态船体坐标系{d}以位于理想轨迹上的航行器重心作为原点Od，坐标轴为xdxd.在不同坐标系中的向量坐标表示通过右下角下标标识，若无标识则默认处于惯性坐标{e}.

图1 航行器运动状态和坐标系Fig.1 AUV′s motion state and coordinate system

其中ED、EB、BD分别表示坐标系原点间位移量，显然可得：

ED=EB+BD

(1)

大地坐标系{e}和理想航行器姿态坐标系{d}间坐标转换矩阵R为：

(2)

式中：ζD为x轴与xd轴夹角.

将式(1)对于时间t进行求导可以得到：

(3)

两边同时乘上坐标转换矩阵R得到：

(4)

(5)

(6)

(7)

式中：ζD为x轴与xd轴夹角；xp、yp为理想路径P的横纵坐标；c(s)为理想路径曲率；s为航行器路程.

ED、EB、BD分别在坐标系{d}或大地坐标系{e}中可以表示为：

(8)

式中xd、yd分别为航行器实际位置与理想路径位置在xdyd两轴方向上的距离.

结合公式(5、8)可以得到：

(9)

将式(2、8)带入到式(9)可得：

(10)

经过化简整理之后得到：

(11)

在大地坐标系之中可得：

(12)

式中：U为航行器速度矢量大小；r为航行器旋转角速度；β为航行器水平和竖直方向速度矢量间的夹角.显然有：

(13)

式中u、v分别为航行器速度U在航行器实际运动坐标系中向ub、wb轴方向上投影的分速度.

将式(12、13)整合可以得到：

(14)

(15)

(16)

如图1，ωU为速度U与x轴夹角ζU变化角速度；ωD为x轴与xd轴夹角ζD变化角速度.

式(15)为航行器的运动学模型，左边变量分别为航行器位置姿态和理想路径情况之间的误差.

观察运动学模型可知，位置误差的变化速度由航行器本身速度状态和预设理想路径变化情况共同决定.此时，预设理想路径是已知信息但无法在控制过程中改变，控制器需要做的是通过改变航行器的速度矢量来达到理想位置.

然后具体到位置和状态变化的表达，都是由该自由度方向上的分速度来决定.

在只考虑平面内三自由度情况，对于航行器动力学关系有[19]：

(17)

式中：u、v、r分别为航行器速度U在航行器实际运动坐标系中向ub、wb轴方向上投影的分速度和航行器本身旋转角速度；m1、m2、m3为考虑附加质量等情况下质量矩阵中的3个等效质量参数；d1、d2、d3为航行器3个自由度方向上的阻尼系数；τuτr为驱动器施加在航行器上的驱动力或力矩.Fd1、Fd2、Fd3为3个自由度上的外界干扰.

第二，从宏观的角度上进行分析。对于一个国家企业的金融结构基本情况一般可以从产业结构、融资结构、资产结构以及市场和金融的开放这五个主要的方面进行分析。由此就能够看出来该结构的演变过程就是一个国家金融结构的演变以及市场结构的变化还有资产在整个国民经济发展中的比重等等，它的演变过程是一个国家金融发展的过程，是一种动态过程，图1是其演变和我国人均GDP的变化曲线。

观察平面内运动学和动力学方程，会发现虽然3个自由度上的位置变化是互不干扰的，但是在动力学方面某一自由度上的速度会对另外一个自由度上的加速度有所影响.可见，模型之中存在相互耦合的特点，主要的体现是在加速度受到其他自由度上运动状态影响.

2 控制器模型

在前面模型建立的基础上进行控制器设计，控制器设计的思路是采用视线法和反步法设计出航行器运动学和动力学控制模型.其中在设计位置控制器的时候，不妨假设航行器速度ud恒定，并以此为基础得到理想的姿态角δ和角速度rd.

由于控制目标是希望航行器按照预设的路径进行跟踪运动，所以最终呈现出来的是位置控制.位置变化状态方程式(15)的输入是速度和角速度.这里首先希望航行器角度ζ能够与预设姿态角δ趋向一致，不妨令李雅普诺夫函数V1为：

(18)

对V1进行求导可以得到：

(19)

(20)

代入式(19)之后整理得到：

(21)

在确定目标角速度rd作为角度姿态的状态方程控制输入之后，还需要确定位置状态方程的控制输入使得位置误差随时间增长而稳定趋向于零.于是不妨令李雅普诺夫函数V2为：

(22)

对V2进行求导可以得到：

(23)

(24)

(25)

代入之后整理得到：

综合公式(20，24，25)得到运动学控制方程：

(26)

在获得理想的位姿角δ和角速度rd结果之后，实际控制输入的是驱动器的力或者力矩.这就需要通过对航行器动力学进行控制器设计，令航行器实际旋转角度ζ和旋转角速度r与预设的姿态角δ和角速度rd分别对应一致，就可以满足路径跟踪的需求.

因此，不妨令李雅普诺夫函数V3为：

(27)

对V3进行求导可以得到：

(28)

(29)

代入之后整理得到：

(30)

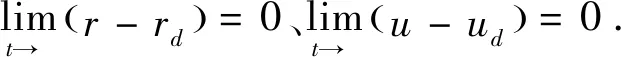
通过反步法的思路去寻找设计合适的控制器，在动力学控制环节考虑到动力学各个自由度之间耦合的情况.将耦合项中基本信息u、v、r通过航行器上传感器进行测量得到，在输入力或力矩之中做一个补偿将耦合项作用抵消，以达到抗耦合干扰的效果.

综上所述，在理论上控制输入符合式(26，29)即可以保证系统的稳定性，并满足水下航行器对路线进行跟踪的需求，至于实际运用效果还需要仿真和实际试验来进行进一步的验证和改进.

3 仿真分析

对控制器进行仿真分析，对航行器控制模型的参数进行适当选取整理之后得到航行器模型为：

式中：Fd1、Fd2、Fd3选择方差为0.005的高斯白噪声；τu、τr属于控制输入的力或者力矩.

对控制器参数进行取值，具体数值大小为：

k3=2，k4=1.25，k5=1

3.1 三角函数型路径

初始条件设计：

r=0.1，u=0.7，x=-2.9，

y=8，ζ=0.3

预设理想路线：

xp=s-1，yp=6cos(0.2s)

yp=6cos(0.2(xp+1)).

在图2中，起始时候水下航行器与理想起点存在差距，这是和设定的初始横向位置x=-2.9，纵向位置y=8一致的.后面可以明显观察到水下航行器的实际路线逐渐基本和理想路线保持一致，并且在终止时刻和理想状态趋向一致.其中图3、4专门将xd、yd随时间t的变化趋势进行比较，和前面路线图结果对照一致.经过了大概6～7 s，在xd轴方向上误差趋向于零，后面基本稳定于零附近波动；经过了大概10～12 s，在yd轴方向上误差趋向于零，后面基本稳定于零附近波动.图5显示的是每一时刻，航行器实际位置与该时刻理想路线点位置的绝对距离d.大约在10 s，航行器绝对位置误差趋向于零，并在后续运动中基本稳定地在零附近波动.可见根据仿真结果显示，文中设计的控制器符合预期设计初衷，也满足水下航行器自主航迹追踪的需求.

图2 航行器实际路径和理想路径对比Fig.2 Comparison of actual path and ideal path of AUV

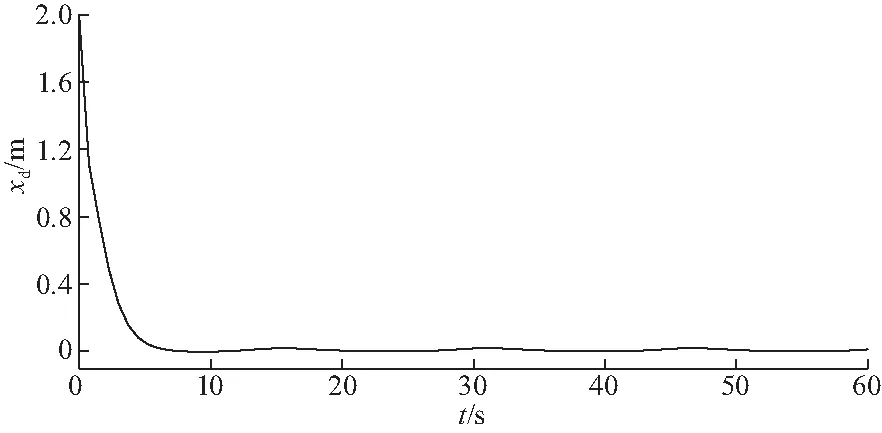
图3 航行器位置误差xdFig.3 AUV′s error xd

图4 航行器位置误差ydFig.4 AUV′s Error yd

图5 航行器位置点和理想路线位置点的距离误差Fig.5 Distance error between the position point of the vehicle and the position point of the ideal route

3.2 线性函数型和圆形路径

初始条件设计：

r=0.1，u=0.7，x=1，y=12.5，ζ=0.3

预设理想路线：

路径以时间为标准从上到下依次分为三段，预先设定航行器从点(0,10)直线行进到点(30,40),再行进到点(40,40)，然后以点(0,10)为圆心做直径为10的圆形环绕运行.

在图6中，起始时候水下航行器与理想起点存在差距，这是和设定的初始位置x=1、y=12.5一致的.后面可以明显观察到水下航行器的实际路线逐渐基本和理想路线保持一致，并且在最后一段围绕预设圆心做圆形环绕运动.其中图7、8专门将xd、yd随时间的变化趋势进行比较，和前面路线图结果对照一致.经过了7 s左右，在xd轴方向上误差趋向于零，中途在82 s左右有一个小的波动，后面基本稳定于零附近；经过了14 s左右，在yd轴方向上误差趋向于零，中途分别在30、82 s左右有一个小的波动，后面基本稳定于零附近波动.图9显示的是每一时刻，航行器实际位置与该时刻理想路线点位置的绝对距离.在12 s左右，航行器绝对位置误差趋向于零，中途分别在30、82 s左右有一个小的波动，并在后续运动中基本稳定地在零附近波动.分析仿真结果可以发现，中间出现的小波动主要是在两段不同路径转折的时间点出现，也能够有效稳定地逐渐趋向于零.可见根据仿真结果显示，文中设计的控制器符合预期设计初衷，也满足水下航行器自主航迹追踪的需求.

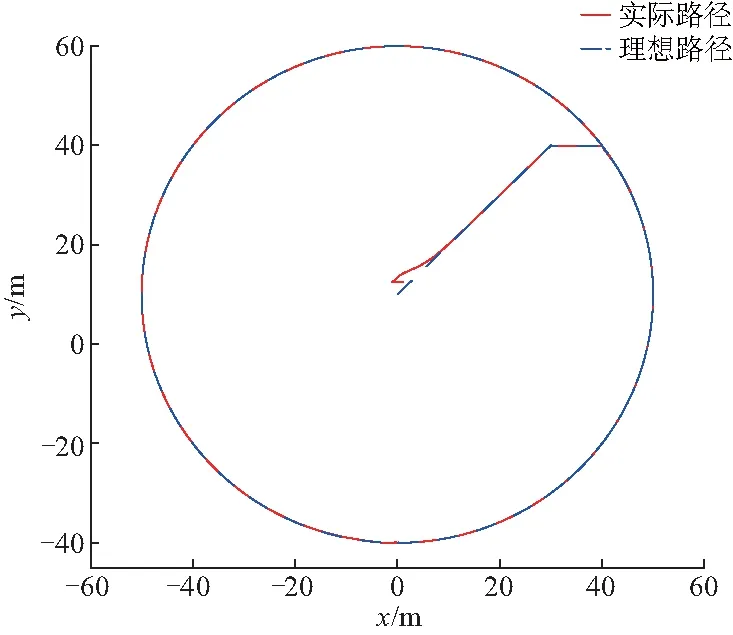
图6 航行器实际路径和理想路径对比Fig.6 Comparison of actual path and ideal path of AUV

图7 航行器位置误差xdFig.7 AUV′s error xd

图8 航行器位置误差ydFig.8 AUV′s error yd

图9 航行器位置点和理想路线位置点的距离误差Fig.9 Distance error between the position point of the vehicle and the position point of the ideal route

4 结论

(1)在模型基础上进行了非线性控制器设计，通过视线法和反步法设计控制模型结构，基本在理论上解决模型存在部分耦合项的困境.最终对于模型进行数值仿真验证了控制模型的有效性.

(2)在满足目标要求的前提下，后续依然有待进一步的装置试验进行验证和改进.航行器本身受到的外界干扰难以实时准确测量，后续可以进一步考虑设计观测器进行预测.对于某些控制中间项的上下限缺乏一定的选择，可能与实际工作中的执行器工作区间有所不符.