二次受力下粘贴钢板加固RC梁抗弯性能分析*

宋 力， 李林果， 樊 成

(大连大学 材料破坏力学数值试验中心， 辽宁 大连 116622)

粘贴钢板加固钢筋混凝土桥梁(RC构件)主要目的是提高构件抗弯承载力，同时改善构件刚度，二者可以形成共同受力的整体，改善原RC构件应力状态，达到补强效果，在实际工程加固已得到广泛的应用和发展[1-3].

目前，国内外学者对钢板加固RC梁已有很多研究.郭文龙等[4]发现加固梁中性轴高度和抗弯刚度随荷载增加均呈非线性变化，且实际计算模型应考虑桥梁损伤的现实状态；张维真[5]对锈蚀RC梁进行加固，发现梁承载力提高明显，但屈服挠度变化不明显；Alam等[6]发现用钢板和粘接剂修复严重剪切损坏的钢板钢筋，可以完全恢复梁的原始剪切能力.

但大多数研究人员只停留在考虑一次受力状态，而忽略桥梁二次受力的影响.一般情况下，RC构件加固是在初始荷载存在时，构件加固前处于一次受力或不完全卸荷状态.为更加贴近实际RC构件加固工程，本文针对二次受力下钢板加固钢筋混凝土梁进行抗弯性能研究.采用数值模拟软件ABAQUS对二次受力下钢板加固RC梁进行模拟，并将得出的模拟数据与试验结果进行对比，分析钢板层数、配筋率和预载量等因素对钢板加固RC梁效果的影响，评估其可靠度和实用性，为修复实际RC桥梁加固工程提供理论基础.

1 试验与有限元分析

1.1 试 验

RC梁为适筋梁，梁长为1 700 mm，截面尺寸为b×h=120 mm×200 mm，纵向受拉、压钢筋分别为HRB400的2φ8、2φ12，配筋率为0.59%，混凝土保护层厚度为30 mm，箍筋型号为HPB300，箍筋配置为φ6@150 mm，混凝土强度等级为C30.单层钢板厚度为2 mm，宽度为120 mm，弹性模量为192 GPa，屈服强度为300 GPa，极限抗拉强度为610 GPa.图1为RC梁试验加载装置，采用三分点加载方式，RC梁试验加载方案如表1所示.

图1 RC梁试验加载装置Fig.1 Loading device for RC beam test

1.2 有限元模型建立

表1 RC梁试验加载方案Tab.1 Loading schemes for RC beam test

图2 RC单轴拉、压应力应变曲线Fig.2 Stress-strain curve of RC under uniaxial tension and compression tests

根据上述条件建立有限元模型，如图4a所示.根据文献[13]，混凝土梁网格划分为30 mm，且种子按边布种.网格划分以及种子布置结果如图4b所示.

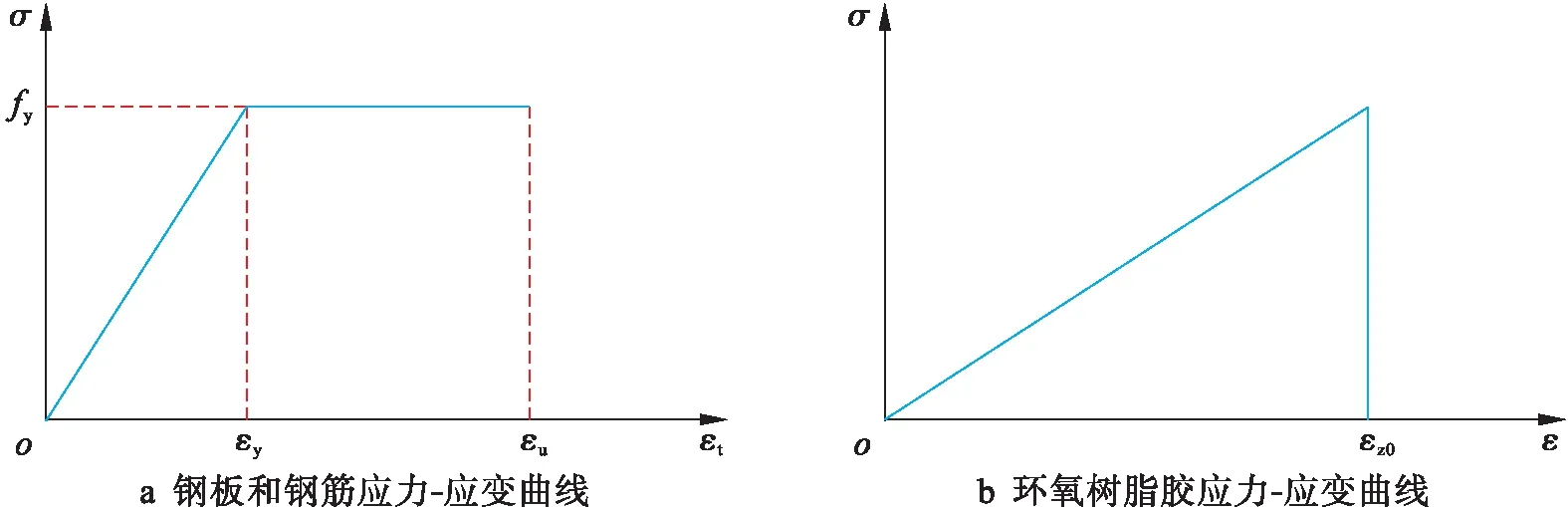
图3 钢材和环氧树脂胶应力应变曲线Fig.3 Stress-strain curve of steel and epoxy adhesives

图4 梁模型有限元建立和网格划分、种子布置Fig.4 Finite element establishment，meshing and seed placement of beam model

2 有限元结果与试验结果对比

表2 有限元结果与试验结果对比Tab.2 Comparison between finite element simulation and test results

3 加固效果影响因素分析

3.1 钢板厚度因素

选取N、O两组数据结合对比梁ML-1进行分析，比较方案如表3所示，有限元模拟结果如图6所示，图7为钢板厚度对梁极限承载力影响柱状图.由图6、7可知：1)无论RC梁是否有加载历程，RC梁极限抗弯承载力都随着钢板厚度的增加而提高；2)当加载历程相同时，钢板厚度对RC梁极限抗弯承载力影响较为明显，且随钢板厚度增加而增大；3)对比NL-4和OL-4发现，无加载历程时，钢板厚度对RC梁的抗弯承载力提高更为明显(NL-1，2，3和OL-1，2，3结论相同)；4)无加载历程时，NL-4和NL-3相对于NL-2和NL-1对提高RC梁的抗弯承载力更大.

3.2 钢板长度因素

表4为钢板长度比较方案.图8为模拟结果.由图8可知，钢板长度为1 300 mm时对RC梁极限荷载提高幅度减弱或不是很明显；钢板长度对挠度影响很小.

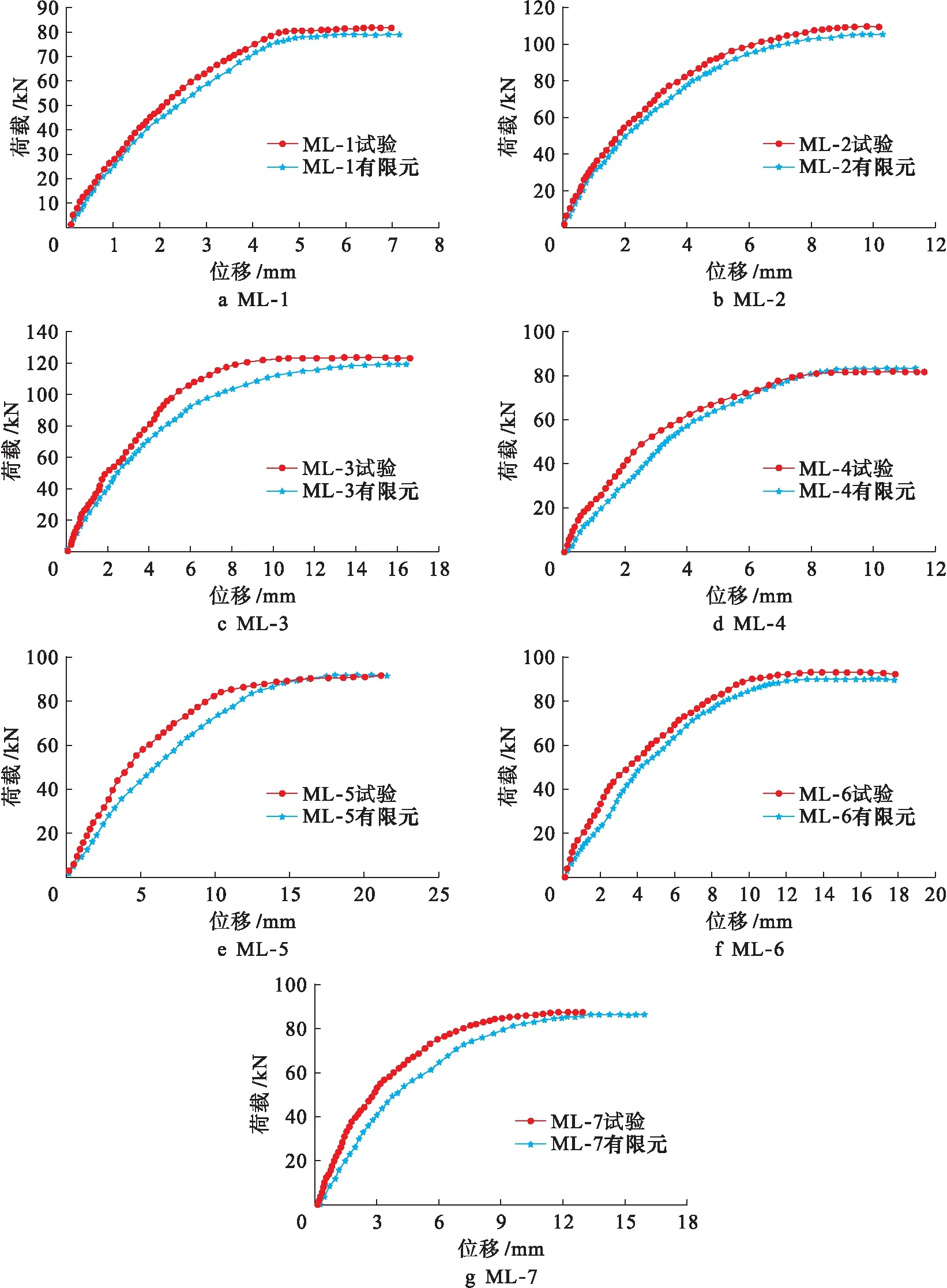
图5 有限元结果与试验结果荷载位移曲线对比Fig.5 Comparison of load-displacement curves between finite element simulation and test results

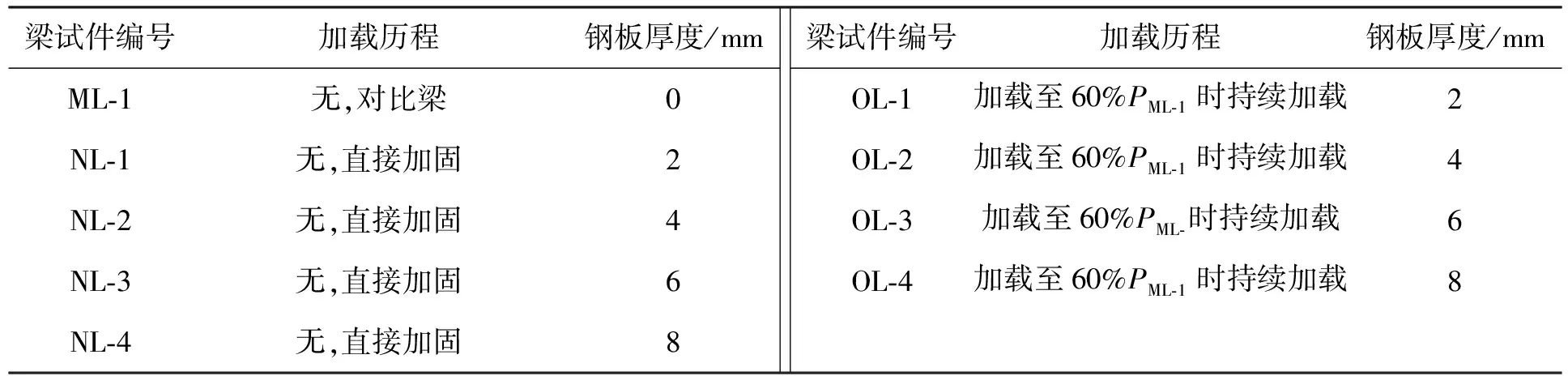
表3 不同钢板厚度方案比较Fig.3 Scheme comparison with various steel plate thickness

图6 钢板厚度和预载量对加固梁荷载位移曲线的影响Fig.6 Effect of steel plate thickness and preload amount on load-displacement curves of reinforced beams

图7 加固厚度与梁极限抗弯承载力关系Fig.7 Relationship between reinforcement thickness and ultimate bending capacity of beams

表4 钢板长度比较方案Tab.4 Scheme comparison for various steel plate lengths

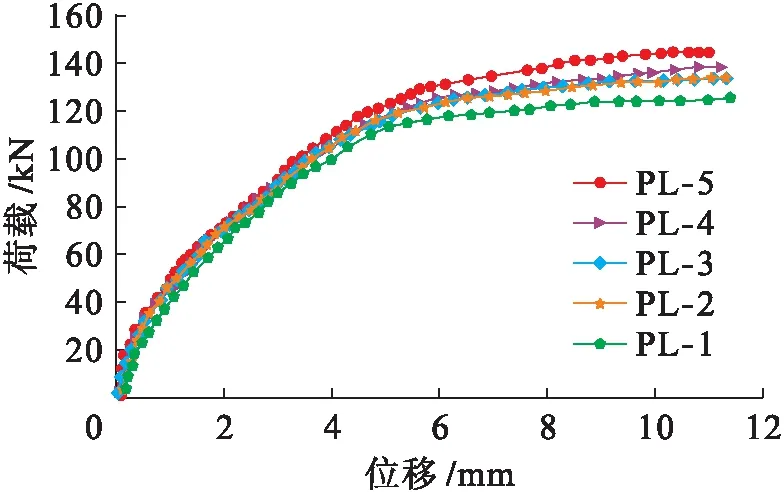
图8 不同钢板长度效果Fig.8 Influence of various steel plate lengths

3.3 配筋率因素

表5为不同配筋率比较方案.图9为有限元结果.由图9可知：1)相同配筋率下，加固梁TL-3(TL-2和TL-1)相对于未加固梁SL-3(SL-2和SL-1)其极限荷载承载力提高45.30%(41.36%和37.94%)；2)钢板厚度相同情况下，RC梁抗弯承载力随配筋率增加而增大，但不明显；3)RC梁最大挠度值减小程度TL组大于SL组，即RC梁更快达到其抗弯承载力.

表5 不同配筋率对比方案Tab.5 Scheme comparison for different reinforcement ratios

图9 不同配筋率影响结果Fig.9 Influence of different reinforcement ratios

4 结 论

本文通过分析得出以下结论：

1) 当二次受力下RC梁配筋率较高时，使用钢板加固RC梁其极限承载力提高明显，即加固效果更好；相对于对比梁而言，增加配筋率对RC梁极限抗弯承载力影响较大.

2) 对二次受力下钢板RC梁加固时，梁抗弯承载力随钢板厚度增加而增大；当预载程度为60%且钢板厚度为6和8 mm时，其抗弯承载力增加很明显，分别为23.00%、25.80%，且钢板长度对挠度影响不大.

3) 存在最佳配板率，使得二次受力下钢板加固RC梁极限承载力提高不再明显或基本不提高.本文中钢板长度为1 300 mm时最好，占总长的86.70%，故实际工程应考虑合理的加固方案以节省钢板原材料.