基于组合变权理论的风电机组状态评估*
2021-08-10华智广
刘 杰, 杨 娜, 华智广
(沈阳工业大学 机械工程学院, 沈阳 110870)
近些年,风力发电行业在飞速发展中面临着诸多困境.多数风场以温度阈值作为风机系统故障预警的标准,极易出现不报或误报等问题,不能充分利用风电机组监控系统的实时数据及早发现风电机组可能存在的故障威胁,同时风电机组的运行维护成本较高,这些使风场在风电机组故障出现后损失惨重[1].如何有效利用风电机组的实时数据对风电机组状态进行评估,发现问题并避免故障的发生是风电机组运行与维护领域最为关切的问题[2].
诸多学者开始对风电机组运行状态评估展开相关研究,李辉等[3]采用层次分析法对风电机组各指标进行赋权,但层次分析法的主观性较强,最终不能准确对风电机组的真实状态做出评估;肖运启等[4]对模糊综合评价策略进行了改进,选用“最大隶属度大于零的最低等级项”原则对风电机组状态进行评价;郭双全[5]基于灰色关联分析方法建立风电机组健康状态评估模型,对部分故障实现提前报警;田树仁[6]将小波变换和粗糙集的方法应用在风电机组变流器诊断中,通过计算欧氏距离的大小确定了变流器的故障类型;万书亭等[7]运用灰色变权理论确定风电机组各指标权重,实现风电机组状态监测,灰色关联分析法比层次分析法更客观,但在确定具有概括性指标权重方面存在一定缺陷.
本文在建立风电机组状态评估体系基础上,运用灰色关联分析与主成分分析相结合的方法计算各指标权重.为了使结果更具合理性,利用变权理论修正,同时引入劣化度确定隶属函数,形成风电机组综合评估流程.将上述方法应用在某风场2 MW风电机组SCADA系统数据中,成功评估了风电机组运行状态,实现故障提前预警.
1 状态评估指标体系与评估方法
以对风电机组运行状态产生影响的相关参数为基础,确定目标层、项目层和指标层共23项风电机组状态评估指标,最终建立如图1所示的风电机组状态评估体系.

图1 风电机组状态评估体系Fig.1 Wind turbine state assessment system
1.1 灰色关联和主成分相结合的组合赋权方法
1.1.1 灰色关联分析法求解指标权重
灰色关联分析法作为衡量因素间关联程度的方法,通过计算各子系统(或因素)样本数据间的关联度,确定各子系统(或因素)间的关系强弱、大小及次序,其优点是对样本量不做要求[8].分析的关联系数表达式为
(1)
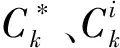
各指标权重计算表达式为
(2)

(3)
式中,m、n分别为关联系数及权重的数量.
1.1.2 主成分分析法求解指标权重
首先需要对原始数据进行标准化,其计算表达式为
(4)
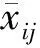
(5)
式中,rij为与zij对应的相关系数.贡献率与组成分载荷计算表达式分别为
(6)
(7)
式中:λi为非负特征量;aij为单位分量.
根据上述主成分分析方法和式(6)~(7),借助SPSS中因子分析等工具箱,确定指标体系中第二层、第一层的权值[9].
1.1.3 确定组合权重
设灰色关联法得到权重为W1=[w11,w12,…,w1t],且满足w1i∈[0,1];设主成分分析法得到权重为W2=[w21,w22,…,w2t],且满足w2i∈[0,1],则组合权重可表示为
W=χW1+δW2
(8)
式中,χ+δ=1,χ、δ根据权重期望值求得,即
(9)
最终χ、δ的计算表达式可表示为
(10)
1.1.4 变权理论修正
风电机组的某些参数严重偏离正常值时,不利于风电机组运行状态的正确判断,为把权重小的指标状态变化对评估结果带来的影响降到最低,需实时调整各指标权重系数以对风电机组的真实状态做出正确评估.本文引入变权理论完成权重修正,变权理论计算表达式为
(11)
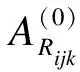
1.2 隶属函数确定
SCADA监控系统数据是反映风电机组状态优秀与否的基础,因此,加入劣化度来表示风电机组实际状态与优秀状态的偏离程度,取值为[0,1].
对于风电机组振动、温度和位移等越小越优型指标,其计算表达式[10]为
(12)
对风电机组压力和速度等中间型指标,其计算表达式[10]为
(13)
式中:x为评估指标的实测值;[xmin,xmax]为指标的正常范围;[xzjmin,xzjmax]为指标的最佳范围.
评估语集是指机组状态综合评价结果的集合,根据风电机组的运行状态最终将评估语集定为“优秀”、“良好”、“注意”、“恶劣”,即
H={优秀,良好,注意,恶劣}={h1,h2,h3,h4}
评估矩阵为
(14)
式中,MRij(j=1,2,3,4)为评估指标Rij在评估集中的状态hi(i=1,2,3,4)对应的隶属度.
为了将结果的差异性降到最小,根据式(12)或(13)对指标劣化度进行计算,最终选用三角形与梯形相结合的分布隶属函数(见图2)确定各评估指标的隶属函数.
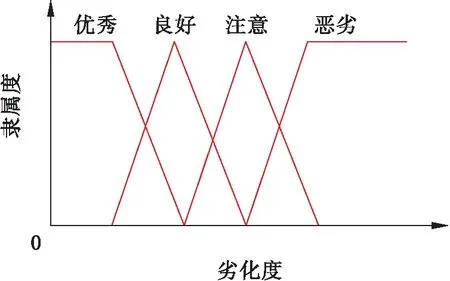
图2 半梯形和三角形组合的隶属函数分布Fig.2 Distribution of half-ladder-shaped and triangular membership function
2 SCADA监控系统数据分析
2017年7月1日14∶01某风场一台2 MW风电机组发生故障停机,以该风电机组SCADA监控系统数据为基础,提取该风电机组故障停机前部分数据(见表1),以此进行状态评估.
2.1 评估方法分析
1) 组合变权.根据表1给出的某风场2 MW风电机组SCADA系统数据进行权重计算.灰色关联分析法及主成分分析法确定的指标权重结果如表2~3所示.
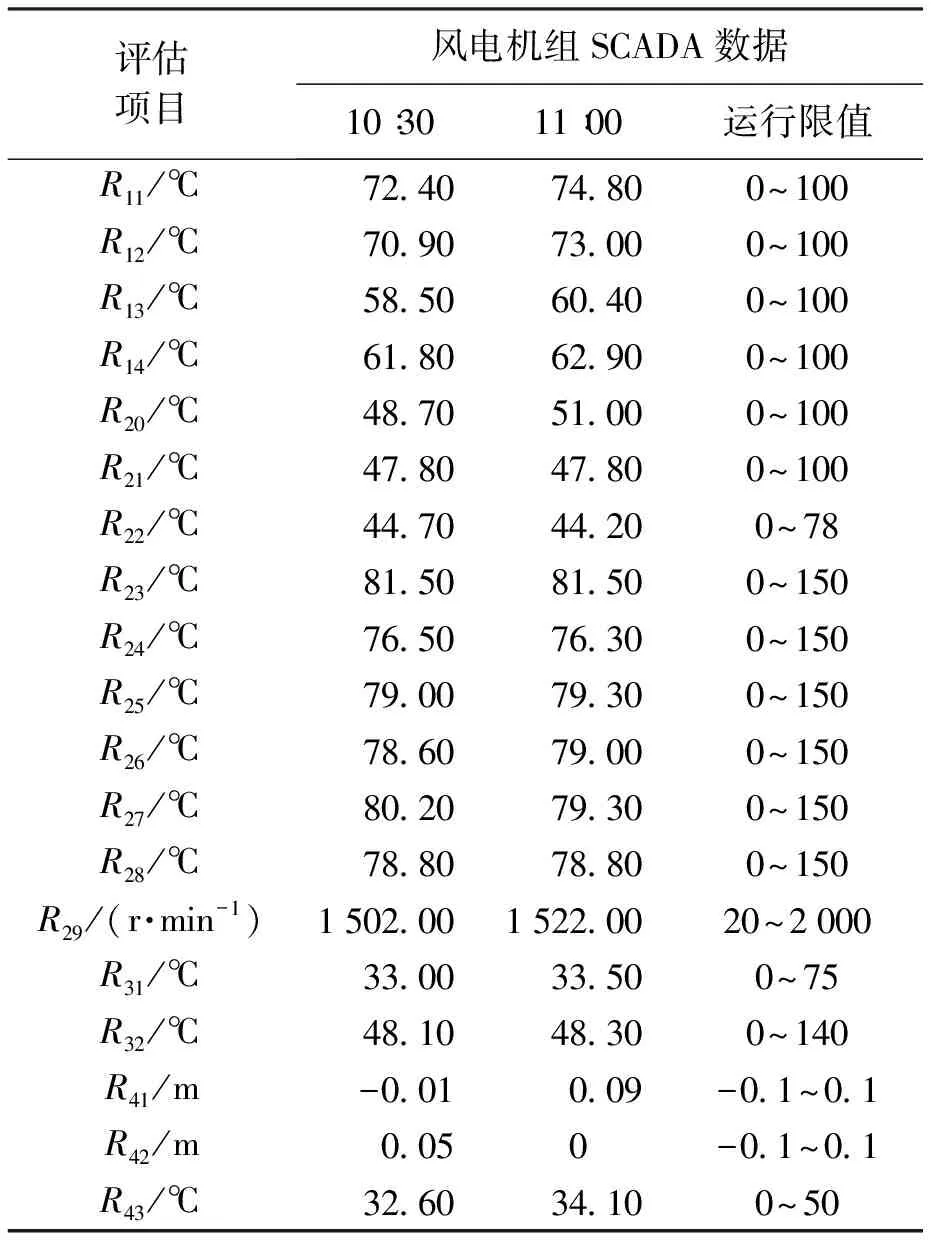
表1 风电机组SCADA数据Tab.1 SCADA data of wind turbines
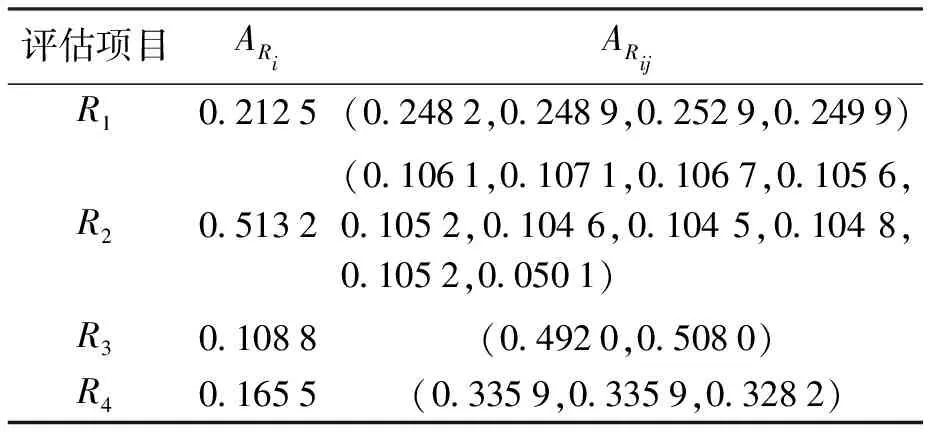
表2 灰色关联分析法确定的指标权重Tab.2 Indicator weights determined by grey correlation analysis method
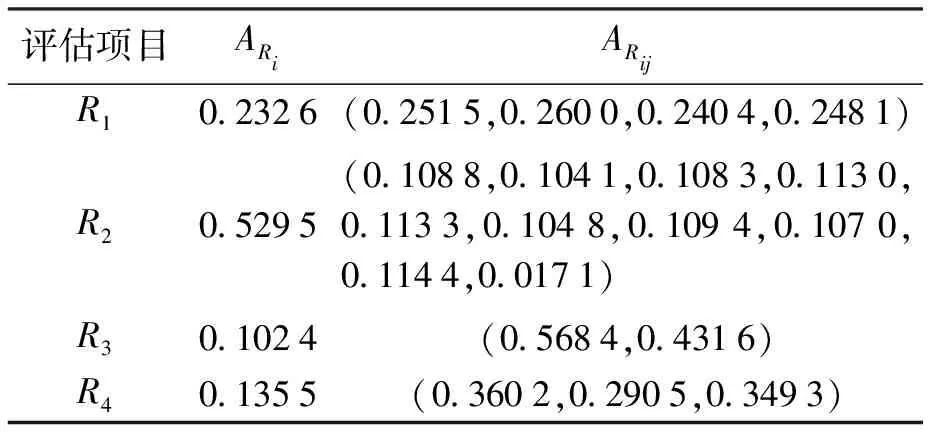
表3 主成分分析法确定的指标权重Tab.3 Indictor weights determined by principal component analysis method
根据式(9)~(10)最终求得χ=0.5,δ=0.5,将上述系数和W1、W2代入公式,得到最终组合权重的表达式为
W=0.5W1+0.5W2
经式(11)变权后的组合变权值结果如表4所示.

表4 组合变权值Tab.4 Combined variable weights
2) 劣化度及评估矩阵.计算各指标的劣化度均为g≤0.9,以10∶30时风电机组齿轮箱为例,得到对应评估矩阵为
3) 状态评估.对齿轮箱R1运行状态进行评估,即
B1=[0,0.010 4,0.568 9,0.420 6]
再对发电机R2、控制柜R3和机舱R4进行评估,结合各部分权重分配最终得到
B=[0.021 0,0.172 3,0.418 5,0.388 2]
根据隶属度最大原则可知B中最大值为0.418 5,判断当前风电机组总体上所处状态为“注意”,同样对11∶00时进行计算得到
B=[0.013 5,0.199 4,0.305 7,0.481 4]
综合上述结果可知,风电机组运行状态依次经历“注意”、“恶劣”.据风场相关人员反映,风电机在14∶01发生故障停机,风电机的状态评估结果与风电机组的实际运行相符,对11∶00时的风电机组各评估指标进行分析,得到R11的劣化度为0.748 0,R29的劣化度为0.770 7,虽仍旧小于0.9,但已经接近最大劣化度,且从表1中可以看出,齿轮箱前轴温度和发电机转速接近限值,故风机出现严重故障的原因主要是齿轮箱前轴温度过高、风机转速过大导致.
2.2 分析结果比较及故障预警点确定
将组合变权方法得到的评估结果与灰色关联法得到的评估结果进行对比,结果如表5所示.由表5可知,两种方法评估结果不一致,11∶00时风机已恶劣运行,而传统方法评估还处于“注意”状态,故改进方法的评估结果与风电机组的实际运行状态相契合.

表5 运行状态评估结果对比Tab.5 Comparison of operating state evaluation results
在10∶30与11∶00两个时刻,采用组合变权方法得到的风电机评估结果分别为“注意”和“恶劣”,于是取10∶30与11∶00间四个时刻数据进行计算,结果如表6所示.
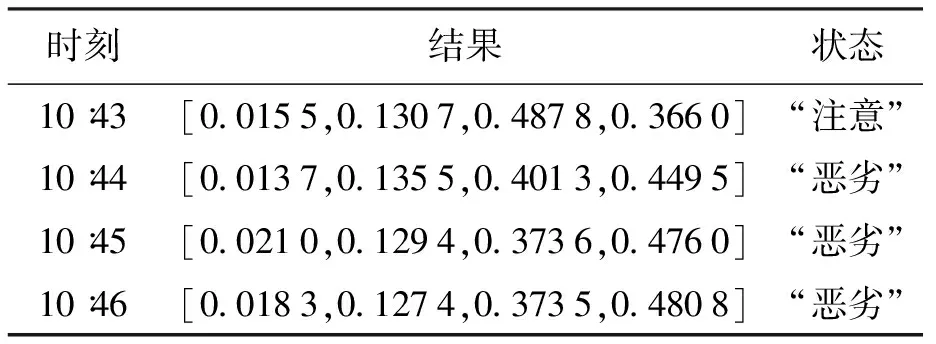
表6 10∶30~11∶00风电机组运行状态评估结果Tab.6 Operating state evaluation results of wind turbines from 10∶30 to 11∶00
由表6可知,10∶44时风机运行开始进入“恶劣”状态,之后一直维持“恶劣”状态,故应在10∶44时启动故障预警.
3 结 论
本文通过分析与风电机组监控系统相关的参数,明确包含目标层、项目层和指标层共计23项指标后,构建风电机组状态评估体系,提出组合赋权再变权方法,并加入劣化度的思想,形成风电机组状态综合评估流程.实例分析表明,变权理论通过对权向量进行动态调整,解决了状态失衡的问题,与传统方法相比,组合变权方法所得评估结果能更好反映风电机组的实际运行状态,最终实现风电机组运行的异常状态识别和故障预警,为管理者及时准确地把握风电机状态提供帮助,避免故障发生.
