过盈失效时轴毂微动的转子系统特性*

周世健， 陈世尧， 李志农，， 陈长征， 卢文秀

(1. 南昌航空大学 无损检测技术教育部重点实验室， 南昌 330063； 2. 沈阳工业大学 机械工程学院， 沈阳 110870； 3. 清华大学 机械工程系， 北京 100084)

在旋转机械中，由于装配质量不高或长期受到振动冲击，会导致轴毂的过盈配合失效.现有的研究主要从轴毂微动展开，分析了微动故障的主要影响因素.卢纯等[1]基于ANSYS建立了重载货车的轮轴有限元模型，分析了轮轴接触区域微动磨损与过盈量的关系，结果表明，随着负载的增大，微动磨损情况会加重；刘庸等[2]建立了轮轴过盈配合结构的微动磨损预测模型，利用该模型研究了微动磨损对接触应力、摩擦剪切应力以及滑移量的影响规律；张远彬等[3]建立了过盈配合结构微动磨损的计算模型，研究了微动磨损对接触压应力、微动滑移幅值等参量的影响；姚兴佳等[4]基于有限元方法，对风电机组轮毂的受力及强度进行了分析，结果表明，使用六面体单元对关键接触区域进行划分，可以准确计算出应力及位移阈值；鹿雪龙[5]建立了轴毂两种装配方式下的有限元模型，分析了不同过盈量、摩擦系数、转速对轴毂接触面径向微动特性的影响规律，以及预紧力对微动特性的影响；冯春宇等[6]结合有限元软件及实际工况对节流阀的阀杆与柱塞的过盈配合进行了建模仿真，分别讨论了配合直径、过盈量和摩擦系数等因素对过盈力的影响；Ma等[7]将轮轨接触问题作为研究对象，分析了有限元模拟的准确性对界面参数和时间步长的影响，同时分析了界面参数与精度之间的关系.这些研究只对轴毂接触微动及滑移的影响因素进行分析，而未对转子系统的振动特性进行分析.一般情况下，这种轴毂微动故障都是在转子旋转过程中出现的，因此，对轴毂微动的转子系统振动特性进行研究，有利于及早发现故障.刘杰等[8]建立了盘轴松动故障转子系统的动力学模型，研究了非稳态油膜力对转盘运动状态的影响及油膜间隙对转子系统振动特性的影响；韦淞瀚等[9]对轴毂的接触模型进行了改进，将轴毂间隙等效为转盘偏心进行动力学特性研究.

本文基于轴毂接触力学模型，对轴毂接触的转子系统进行有限元仿真，分析了当轴毂微接触时，过盈量、转速以及摩擦系数对轴毂接触应力的影响.进一步分析了转速改变时，系统振动特性的变化规律，并通过实验验证有限元建模仿真结果.将该有限元模型用于轴毂接触的系统振动特性研究，具有很好的可行性.

1 轴毂Hertz接触力学模型

在转子系统中，当轴毂接触采用过盈方式进行装配时，可依据Hertz理论对轴毂接触的状态进行分析研究.使用Hertz接触理论时假设：1)转轴与转盘均为完全弹性材料；2)接触体材料绝对均匀，且各向同性；3)转轴与轮毂接触表面均是光滑的；4)转轴与轮毂接触过程中不存在刚体位移；5)转轴与轮毂接触时不传递切向力.

为了将问题进行简化，可将转轴与轮毂的接触当成一对轴线平行的圆柱内接触，如图1所示.

图1 圆柱内接触模型Fig.1 Contact model in cylinder

图1中，两个圆柱体的半径分别为R1、R2，弹性模量和泊松比分别为E1、v1，E2、v2.在两接触体上施加大小为P的压力，接触面上会因压力的存在而出现接触应力，接触应力大小分布不等，会表现出从接触中线到两侧逐渐减小的趋势.因此，实际的接触压力分布为半椭圆形.根据弹性理论可知，当压力为零时，两个圆柱内接触为线接触，当压力增大后，接触面积将会变为一个较窄的长矩形，宽为2b，长为L.根据赫兹公式，可计算出接触区域的半宽为b，其计算公式为

(1)

最大的接触应力位于接触区域的中线上，其值为平均压力大小的4/π.若两圆柱在接触过程中，接触面上的接触应力为σHmax，则接触面上的合力为πσHmaxbL/2.此时，接触体上施加的压力P等于接触面上的合力，即

(2)

则接触压力的基本公式为

(3)

将式(1)代入式(3)，可得

(4)

2 轴毂接触有限元建模仿真

2.1 有限元求解

使用有限元法求解弹性接触问题时，接触压力的分布为非线性，产生的摩擦力也为非线性，求解过程为接触状态变化后反复迭代的过程.基于弹塑性增量理论[10]的非线性有限元方法，分析转轴、轮毂过盈接触区域的接触应力.弹塑性增量理论模型可以从以下5个关系进行求解.其中，应变分解关系为

(5)

(6)

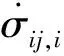
(7)

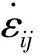
(8)

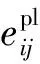
(9)

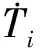
2.2 有限元仿真分析

在过盈配合的转子系统中，接触压力是影响轴毂接触微动的一个重要参数，接触压力主要由装配过盈量来实现.当过盈量不足或因长期的交变载荷使材料发生塑性变形时，轴毂之间会产生接触间隙从而引起微动现象.同时，摩擦系数、转速引起的离心力变化也会引起轴毂配合面之间产生局部微动区域.因此，通过建立轴毂接触有限元模型，分析了过盈量、转速及摩擦系数对轴毂接触应力的影响.当过盈力不足时，轴毂微动现象会对转子系统的振动特性产生影响.

轴毂的主要参数为：转盘的外径为76.2 mm；内径为9.5 mm；转盘两侧的凸缘厚度为5 mm.转盘、转轴的材料为45号钢，密度为7 890 kg/m3，泊松比为0.269.

图2为轴毂接触有限元模型.首先在三维建模软件中建立轴毂接触的几何模型，导入ANSYS有限元分析软件中；其次设置轴毂接触副为摩擦接触，接触过盈量在offset中调整.转轴两侧为弹簧支撑，刚度为1.3×107N/m，阻尼为7002N·s/m.在转轴上添加旋转副，并且设置轴速.

图2 轴毂接触有限元模型Fig.2 Finite element model of shaft-hub contact

图3为不同过盈量时轴毂接触应力随时间的变化曲线.σHmax为轴毂接触区域的最大接触应力，σHmin为最小接触应力.在每幅图中，0～1 s为转盘从0 rad/s加速至20 rad/s的过程.由图3可知，随着时间的延长，σHmax呈现先减小后增大至稳定的变化趋势，σHmin没有明显的变化.转速的增大会引起离心力发生改变，从而导致接触应力随之改变.图3a中，σHmax达到稳定时为1 070 MPa，图3e中，σHmax达到稳定时为1 190 MPa，随着过盈量的增大，σHmax也会变大，即过盈量和转速的增大都会引起接触应力的改变.

图4为轴毂接触应力随过盈量的变化曲线.依据装配过程中过盈量的选取标准，选取过盈量分别为0.01、0.012、0.014、0.016、0.018 mm时，分析在标准过盈量内的应力变化.由图4可知，过盈量增大会引起σHmax及σHmin近似线性增大.

图5为不同转速时轴毂接触应力随时间的变化曲线.在每幅图中，0～1 s为转盘从0 rad/s加速至20 rad/s的过程.随着时间的延长，σHmax呈现先减小后增大至稳定的变化趋势，σHmin没有明显的变化.图5a中，σHmax达到稳定时为1 079 MPa，图5f中，σHmax达到稳定时为830 MPa，随着转速的增大，σHmax会发生变化.图6为轴毂接触应力随转速变化的规律曲线.由图6可知，转速的增大会引起σHmax的减小，σHmin的减小不是非常明显.当转速增大时，转盘受到的离心力会增大，因此轴毂之间的接触压力会减小.图7为轴毂接触应力随摩擦系数变化的规律曲线.由图7可知，摩擦系数的变化不会引起σHmax发生明显的变化，同时σHmin也无明显变化.

图3 不同过盈量时轴毂接触应力随时间的变化曲线Fig.3 Variation curve of contact stress between shaft and hub with time under different interference magnitudes

图4 接触应力随过盈量的变化曲线Fig.4 Variation of contact stress with interference magnitude

由图4、6～7可知，转速及过盈量的变化会引起轴毂接触应力发生明显的改变.摩擦系数的改变对接触应力的影响是非常小的.

图5 不同转速时轴毂接触应力随时间的变化曲线Fig.5 Variation curve of contact stress between shaft and hub with time at different rotating speeds

图6 接触应力随转速变化曲线Fig.6 Variation curve of contact stress with rotating speed

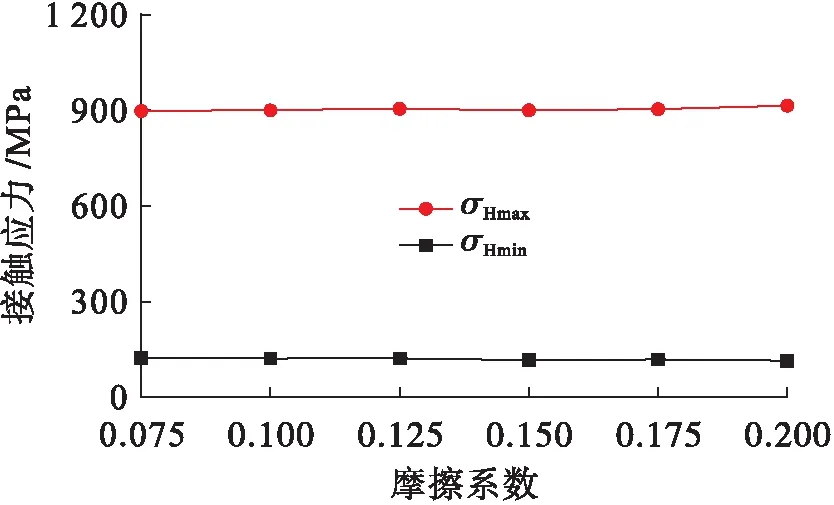
图7 接触应力随摩擦系数变化曲线Fig.7 Variation curve of contact stress with friction coefficient

图8为不同转速时轴毂转速差的变化图.由图8可知，当转速发生变化时，轴毂之间的转速差会发生明显的变化.转速越大，转速差会有一定幅度的增大，同时波动幅度也会变大.

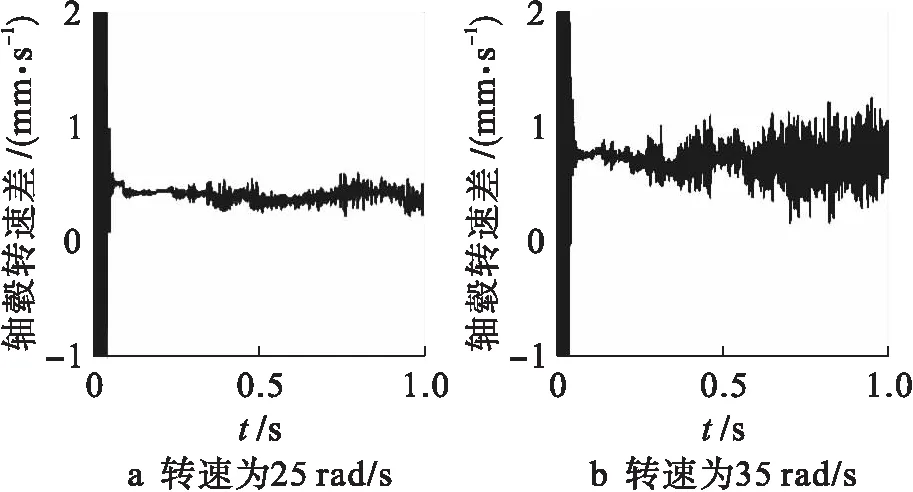
图8 不同转速时轴毂转速差变化图Fig.8 Rotating speed difference between shaft and hub at different rotating speeds

图9～10分别为不同转速时的时频图.时域图中存在明显的拍振现象，转速不同时，拍振周期会发生变化.拍振现象的产生是由于轴毂转频相差很小，两个信号叠加后产生.在两幅频谱图中都可以看到两个相差很近的频率成分，图9b中的频率为25 Hz和24.82 Hz，图10b中的频率为35 Hz和34.87 Hz.当转速变大时，因离心力增大，导致轴毂接触压力减小，时域图中的振幅也会相应地有所变大.

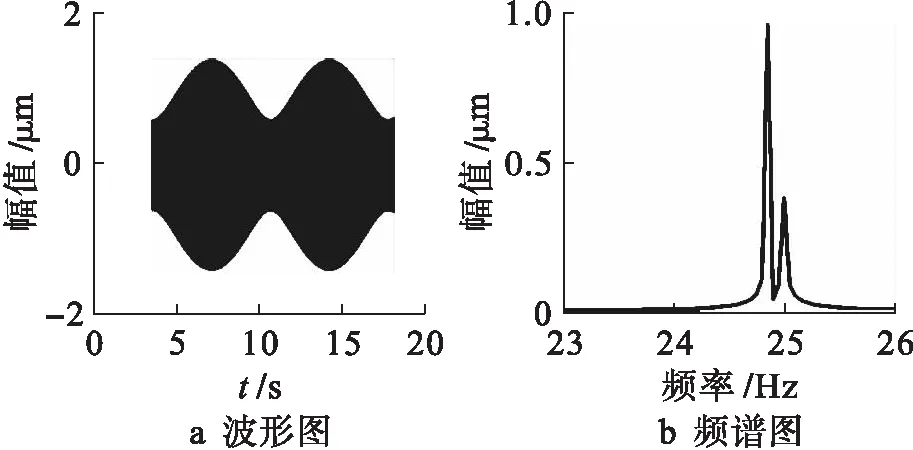
图9 转频为25 Hz时系统时频图Fig.9 System time-frequency figure at rotating frequency of 25 Hz

图10 转频为35 Hz时系统时频图Fig.10 System time-frequency figure at rotating frequency of 35 Hz

图11为不同转速时盘心轨迹图.图11中的轨迹为规则的椭圆形，随着转速的增大，盘心轨迹的x、y轴上的幅值均有所增大.

图11 不同转速时盘心轨迹图Fig.11 Tracks of disc center at different rotating speeds

3 实验研究

为验证轴毂微动的转子振动特性有限元仿真结果，设计了微动故障转子实验系统.实验系统由ZT-3转子实验台部分、传感器部分及信号采集显示部分等组成.

图12为转子实验台，实验台中包含电机部分、联轴器部分、盘轴部分及轴承支撑部分等.实验台的电机可实现0～10 000 rad/min的无极调速，满足轴速调整的要求.转轴的直径为9.5 mm，转盘外径为76.2 mm，转轴两支撑座之间的间距为422 mm，转盘质量为0.612 kg.为分析不同转速时，轴毂无过盈力接触转子系统的振动特性，可以通过调整转轴速度进行实验.实验中转盘结构如图13所示.转盘由内圈和外环两部分组成，同时这两部分通过锥面接触，由内圈旋进来调整转盘与转轴之间的过盈力大小.实验中不考虑转盘轴向位移的影响.

图12 ZT-3转子实验台Fig.12 ZT-3 rotor test bench

图13 转盘结构Fig.13 Rotary disk structure

图14为转速为23 rad/s时转子系统时频图.图14a中有明显的拍振现象，图14b中不仅存在相差较小的频率，还存在明显的多倍频成分.轴毂的转频分别为22.48 Hz和22.43 Hz，由于转频差的存在所以会出现拍振特性.图15为转速为30 rad/s时转子系统时频图.图15a中也存在明显的拍振现象，图15b中存在轴毂转频分别为29.18 Hz和29.12 Hz.同时，频谱图中依然存在多倍频成分，但多倍频的幅值相对于转频的幅值很小.

图16为转速为41 rad/s时转子系统时频图.图16a中没有明显的拍振现象，由图16c中的频谱图局部放大图可知，轴毂的转频分别为41.1 Hz和41.07 Hz.由图16b、d可知，多倍频的幅值相比于转频的幅值非常小.对比分析图14～16可知，当轴毂间过盈力不足时，轴毂之间会出现转速差，系统的时域图中会有明显的拍振现象.在转速较低时，频谱图中有明显的多倍频，当转速增大后，拍振周期会发生明显的变化，同时频谱图中的多倍频成分变得非常小.

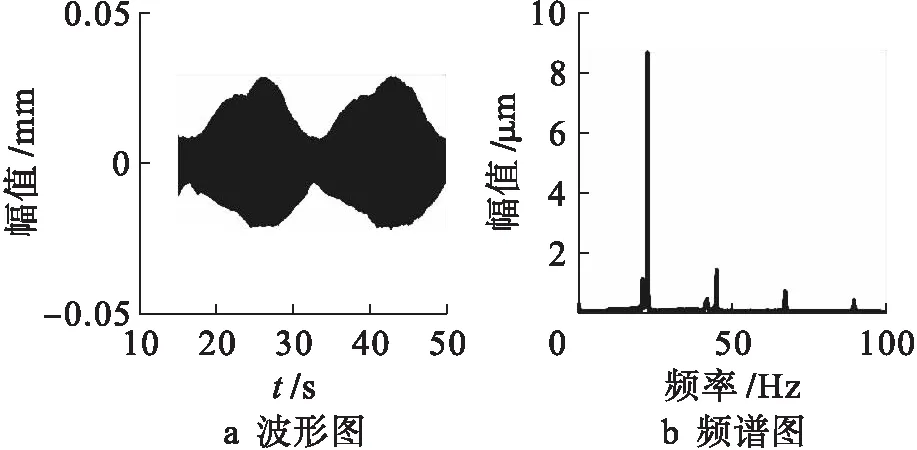
图14 转速为23 rad/s时系统时频图Fig.14 System time-frequency figure at rotating speed of 23 rad/s

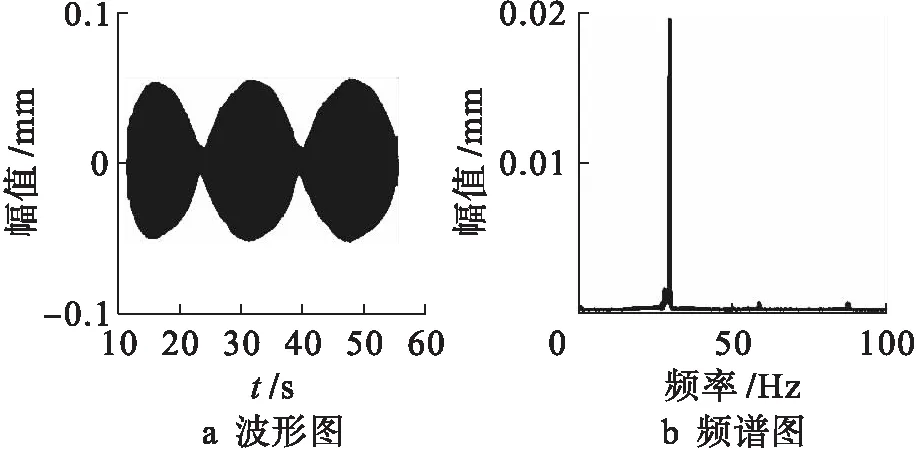
图15 转速为30 rad/s时系统时频图Fig.15 System time-frequency figure at rotating speed of 30 rad/s

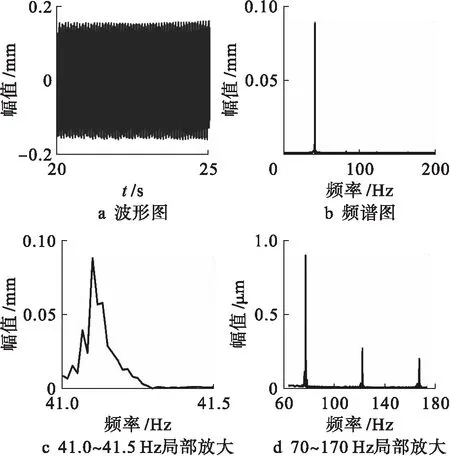
图16 转速为41 rad/s时系统时频图Fig.16 System time-frequency figure at rotating speed of 41 rad/s

图17为三种不同转速时盘心轨迹图.由图17可知，当转速较低时，转盘的盘心轨迹存在明显的锯齿状波动.当转速增大后，盘心轨迹会变为规则的圆形，同时锯齿状的波动特性会消失.通过频谱图中的多倍频变化及盘心轨迹可知，在转速较低时，因轴毂过盈力的不足，轴毂之间会存在碰磨的可能.当转速增大后，只存在轴毂转速差，以及轴毂微动摩擦.

图17 三种不同转速时盘心轨迹图Fig.17 Tracks of disc center at three different rotating speeds

4 结 论

基于轴毂接触的力学模型，本文对轴毂的有限元模型进行了仿真研究，分析了过盈量、转速及摩擦系数对轴毂接触应力的影响.同时分析了过盈力不足时，转速对轴毂微动转子系统振动特性的影响.最后通过实验验证了转速对轴毂微动转子系统振动特性的影响，得出以下结论：

1) 轴毂过盈配合时，在转盘的升速过程中，轴毂之间的最大接触应力会出现先减小后增大至稳定的波动过程.

2) 在一定范围内，随着轴毂间过盈量的增大，轴毂间的最大接触应力会呈现类似线性增大现象.转速增大时，最大接触应力会出现减小的趋势.摩擦系数的改变对轴毂接触应力不会产生明显的影响.

3) 当轴毂间过盈失效时，轴毂之间会因微动摩擦而存在明显的转速差.转速较低时，时域图中会出现拍振特性，频谱图中存在转频及多倍频成分，盘心轨迹中存在锯齿状波动.转速增大后，拍振周期会发生明显改变，频谱图中的多倍频成分也会减至很小，盘心轨迹变为规则的圆.同时转速增大会引起轴毂接触应力减小，时频图中的振幅均会明显增大.