基于量子粒子群优化算法的云计算负载均衡分析*
2021-08-10李祥琴罗传军
李祥琴, 罗传军, 杨 利
(1. 荆楚理工学院 计算机工程学院, 湖北 荆门 448000; 2. 湖北省荆门市电子政务信息中心, 湖北 荆门 448000; 3. 池州学院 大数据与人工智能学院, 安徽 池州 247000)
随着计算机应用范围的不断拓宽,每天会涌入大量数据,单机运行速度已经达到了瓶颈,无法满足海量数据处理的要求,在此背景下,云计算技术应运而生[1].云计算技术是多种技术的集成,主要包括:网格计算技术、分布式处理技术、并行计算及人工智能技术,其基于互联网技术将各种不同的资源打包成服务,通过收费方式提供给用户[2-3].由于云计算节点资源数量有限,且比较昂贵,因此需尽量使云计算资源上负载保持一种动态均衡,故云计算资源利用率达到最大化是云计算领域中的一个重要研究方向[4-5].
针对云计算负载均衡问题,出现了许多类型的云计算负载均衡方法[6].最初,人们采用穷举式搜索算法对负载均衡问题进行求解[7],但当云计算资源负载规模较大时,计算复杂度会呈指数形式增长,在短时间内很难搜索最优云计算负载均衡方案,不能满足现代海量数据处理的要求.随着群智能技术研究的不断深入,出现了许多类型群智能优化算法,它们模拟自然界生物的群体搜索特性对问题进行求解,如基于禁忌搜索算法、基于蝙蝠算法、基于蚁群算法及基于猫群优化算法的云计算负载均衡方法等[8-10].上述算法均需建立云计算负载均衡问题的相关数学模型,然后找到云计算资源负载最优分配方案[11-12],故在实际应用中,这些群智能优化算法存在搜索效率低、局部最优解搜索停滞、求解精度低等问题[12].
针对当前云计算负载均衡方法的节点出现过负载或者长期空闲的局限性,本文设计了基于量子粒子群优化算法[13]的云计算负载均衡方法,并与其他群智能优化算法进行了仿真对比实验,证明了云计算负载均衡方法的可行性和优越性.量子粒子群优化算法能够避免其他群智能优化算法在求解过程中存在的缺陷,提高了云计算节点资源的利用率,使节点负载更加均衡,能够获得更为理想的云计算负载方案.
1 云计算系统负载均衡
1.1 云计算系统基本结构
云计算系统是一种为了解决海量任务的并行式处理系统,与单节点计算机系统相比,其工作模式具有比较明显的差异,云计算将服务器、存储设备、网络、打印机等抽象成资源,任何用户都可按自己的需求申请相应类型服务,能够满足不同用户服务质量要求.云计算系统的基本结构如图1所示.

图1 云计算系统的基本结构Fig.1 Basic structure of cloud computing system
1.2 云计算系统负载均衡数学模型
设用户任务集合为S={s1,s2,…,sm},其中,si为第i个用户的任务;云计算系统所有节点资源组成的集合为R={r1,r2,…,rl},其中,rj为节点资源的虚拟设备,其与实际相关物理设备相对应;云计算中具体物理设备集合为D={d1,d2,…,dn},dk为第k个物理设备.以上三个参数的相互关联集合可表示为
C={S,R,D,Mtr,Mrd}
(1)
式中:Mrd为云计算资源与物理设备之间的映射关系;Mtr为用户任务与云计算系统资源之间的映射关系.
设第i个用户的任务被分配到第j个资源上,云计算节点资源采用第k个物理设备处理该任务,任务在相应物理设备处理时间为E(si,Mtr,dk),物理设备dk开始执行第i个用户任务时间为ST(dk),则第i个用户的任务完成时间为
F(si,Mtr,dk)=ST(dk)+E(si,Mtr,dk)
(2)
物理设备dk上任务完成时间之和为
(3)
式中,cik=1为si在dk上执行;否则cik=0.云计算负载均衡求解就是找到一个用户任务完成时间最少的方案,即
(4)
2 负载均衡方法
2.1 标准粒子群优化算法

(5)
(6)
式中:w为权值;τ1、τ2为加速因子;β为搜索时间间隔.
2.2 量子粒子群优化算法
标准粒子群优化算法与其他智能优化算法一样,存在不同程度的局限性,如存在搜索后期效率低、找最优解的概率低等问题.为了克服标准粒子群优化算法的缺陷,提出了量子粒子群优化算法.

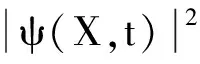
(7)
在量子力学中,粒子运动的动力学方程为
(8)
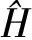
对量子粒子群优化算法的粒子收敛行为进行分析可知:算法中存在一个以点P为中心的某种形式的吸引势,把点P称为粒子的吸引子.通过在吸引子中建立一维势阱,推导出粒子在势阱中的定态薛定谔方程,解得粒子出现在相对吸引子位置Y的概率密度函数为
(9)
式中,L为粒子与种群平均最优解间的距离.
引入蒙特卡罗随机模拟方法测量粒子的位置,粒子在以P点为中心的一维势阱中运动,其位置可表示为
(10)
式中:u为一个随机数;XP为当前P点位置.
根据式(5)、(6)和(10)可以得到具有量子行为的粒子进化方程,即
(11)

为了测试量子粒子群优化算法(QPSO)的优越性,本文采用标准粒子群优化算法(PSO)进行了对比分析.选用的标准测试函数为Griewank和Rosenbrock,其定义分别为
(12)
(13)
图2为两种算法在不同测试函数下的对比分析结果.由图2可知,相对于粒子群优化算法,量子粒子群优化算法能够找到更优的解.
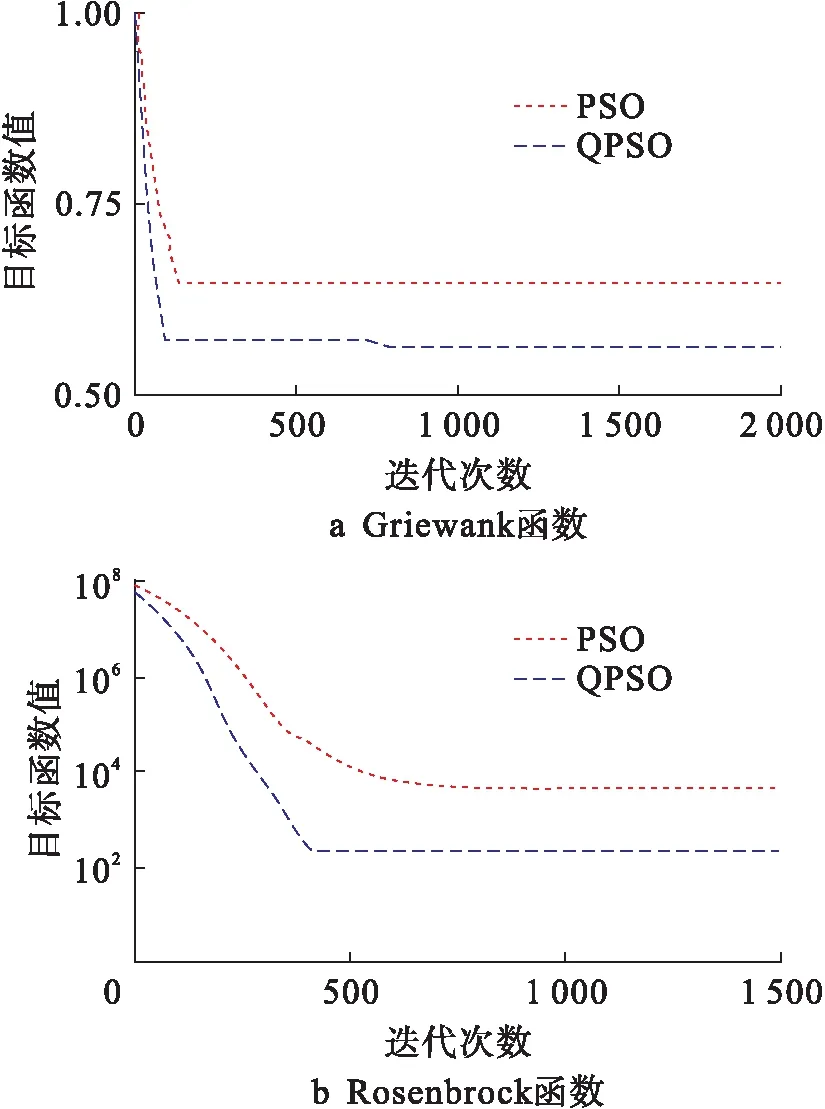
图2 量子粒子群算法和粒子群算法的性能对比Fig.2 Performance comparison between QPSO algorithm and PSO algorithm
2.3 云计算负载均衡方法
本文引入量子粒子群优化算法对云计算负载均衡问题的数学模型进行求解,具体步骤如下:
1) 建立云计算系统,确定各种云计算资源的数量、云计算任务数量以及各种云计算资源的处理能力;
2) 收集用户任务,对云计算用户调度任务进行分解,划分为不同大小的云计算任务;
3) 根据云计算任务、云计算资源以及物理设备之间的对应关系,以用户任务完成时间最短为目标函数,构建云计算负载均衡问题的数学模型;
4) 引入量子粒子群优化算法对云计算负载均衡的数学模型解进行搜索,找到最优的云计算负载均衡方案.
3 云计算负载均衡方法性能验证
3.1 实验参数设置
为了分析量子粒子群优化算法云计算负载均衡方法的性能,采用Matlab 2017工具箱编程云计算负载均衡程序,云计算系统中的节点资源类型为5类.量子粒子群优化算法的参数设置为:量子粒子数为20,搜索扩张系数为0.25,最大迭代次为300.
3.2 实验结果与分析
3.2.1 任务完成时间对比
选择文献[14]和文献[15]的云计算负载均衡方法进行对比实验.每一种云计算负载均衡方法均进行5次仿真实验,以增加实验结果的可靠性,3种云计算负载均衡方法的任务完成时间对比结果如图3所示.由图3可知,基于量子粒子群优化算法的云计算负载均衡方法的任务完成时间最短,而文献[14]和文献[15]的云计算负载均衡方法的任务完成时间均有一定的延长,量子粒子群优化算法提升了任务完成的速度.
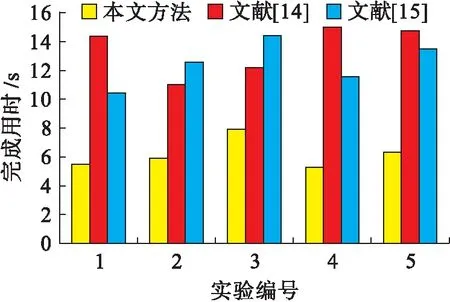
图3 云计算负载均衡方法的负载完成时间Fig.3 Load completion time of load balancing methods for cloud computing
3.2.2 资源负载分配结果对比
3种云计算负载均衡方法的资源负载分布结果对比如图4所示.根据图4结果可知,量子粒子群优化算法的云计算资源负载十分均衡,出现少量的“过负载”或者“空负载”现象;而文献[14]和文献[15]的云计算负载均衡方法均出现了大量“过负载”或者“空负载”现象,这表明量子粒子群优化算法可以保证云计算负载均衡,提高了云计算资源利用率.
3.2.3 最优方案迭代次数对比
量子粒子群优化算法与文献[14]和文献[15]的云计算负载均衡方法找到最优方案的迭代次数对比如表1所示.由表1可知,量子粒子群优化算法找到最优方案的迭代次数均值明显少于文献[14]和文献[15]的云计算负载均衡方法,量子粒子群优化算法加快了云计算负载均衡问题的求解速度,可以满足大规模云计算负载均衡应用要求.
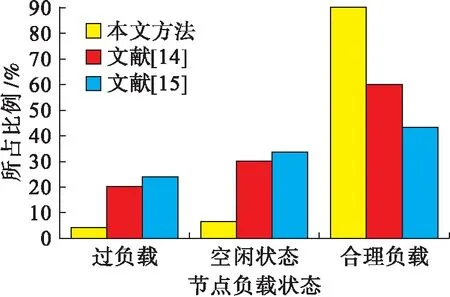
图4 云计算负载均衡方法的负载分布对比Fig.4 Comparison of load distribution among load balancing methods for cloud computing

表1 最优方案的迭代次数对比Tab.1 Comparison of iteration times for optimal solution
4 结 论
负载均衡是云计算系统中的一项关键技术,针对当前云计算负载均衡方法存在的不足,为了获得更优的云计算负载均衡效果,本文设计了基于量子粒子群优化算法的云计算负载均衡方法.测试结果表明,量子粒子群优化算法可以获得理想的云计算负载均衡方案,使云计算节点之间的负载更加均衡,加快了用户任务完成速度,具有一定的推广价值.
