初中“数学活动”育人的教学过程构建

顾广林 帅建卓

【摘 要】 初中“数学活动”将抽象的知识用鲜活的实践体现.育人的教学过程应该围绕真实情境而展开，解决问题的的过程要引导学生在“做”中体验建构，重视问题的提出和建模等数学化过程，使学生在问题解决中深化理解和拓展知识，提升数学能力和素养.

【关键词】 “数学活动”;教学过程;问题解决;教学结构

初中“数学活动”分布在教材章末，具有鲜明的“活动”特点，本质是基于真实情境的问题解决.问题的条件需要自己探索，是常规解题的逆向思考.因此，“数学活动”教学应该有别于常规数学教学，教学过程应该围绕蕴含数学本质问题的真实情境展开，引导学生在“做”中主动体验建构，能够在真实情境的问题解决中深化理解和结构化知识，提升迁移应用能力，发展数学素养.文章拟结合《“数学活动”——超市中的数学》从教学主题、教学准备、组织活动等方面阐述“数学活动”教学过程的构建.

1 确定“数学活动”教学主题

“数学活动”突出数学与生活的关联，提高学生以数学的眼光看待、分析及理解情境的能力，提高学生的独立思考、合作交流、发现问题、提出问题、抽象、建模等能力和素养，与学科教学在育人功能上相互补充.“数学活动”的情境有的主题明确，学生直接探索问题解决方法.有些情境结构复杂，具有较强的开放性，学生能够提出许多问题作为研究内容，需要明确活动的主题，活动才有针对性.对于“超市中的数学”，要求学生去超市考察，提出系列数学问题，比如，怎样设计包装纸箱使所用材料最少？这个超市应该设置几个收款通道？每天各个时段分别开放多少个收款通道？进货时选择哪些型号的商品最畅销？……，不同的主题为开展“数学活动”提供丰富的教学资源.文章拟从活动主题——开放几个收款通道，谈谈教学过程的构建.

2 制定“数学活动”教学目标

“数学活动”是一个完整的学习单位，是一个微课程，更能凸显育人价值.有了主题就要设计教学目标，目标定位作为教学活动的第一要素及最终归宿，要在数学活动课程总体目标统领下，结合活动内容、学生发展、师生活动等制定适当的活动目标.从知识和技能的角度分析，“数学活动”教学在应用中要深化理解和拓展延伸所学内容，认识数学知识的本质.从育人角度思考，要体现“数学活动”培养学生的应用意识、创新能力和社会交往能力及自我意识的唤醒、数学文化认同等育人价值.为此，确定本次“数学活动”教学目标：学生能够从超市情境中提出问题，能够根据主题拟定调查方案收集数据，培养学生提出问题、信息处理和交往等能力;在选择模型解决问题过程中深化对方程、不等式和函数等知识的理解，提升实际问题数学化的能力.

3 “数学活动”教学前期准备

“数学活动”与常规教学有所区别，需要一定的实施条件，课前应该准备好必要的硬件、软件等活动工具或素材.根据主题和学生可能提出的问题，需要了解学生活动的认知基础，具体分析解决问题过程中，学生已经具备哪些知识、技能和经验.学生能否灵活运用这些知识，也就是是否具备一定的知识迁移能力，需要根据学情对相关知识和能力进行适当的的先行组织，这样才能准确把握教学的逻辑起点，同时根据差异情况，预设“脚手架”.有些“数学活动”需要社会调查或实际测量，要加强安全管理，协调好相关场所.外出实践活动也需要组建活动小组，明确各自的任务，分工协作.解决“开放几个收款通道”的问题，学生需要能够解决“至少开放几个闸口（检票口）”的认知基础，如果欠缺，适当复习，以便解决更深层次的问题.本次“数学活动”需要以小组学习的方式走进超市，根据主题进行不同视角下的调查统计，收集相关数据，需要指导小组策划调查方案.

4 “数学活动”教学过程设计

“数学活动”教学过程设计需要宏观分析活动过程，分析“数学活动”教学结构，设计要点，能够培养哪些能力和素养，如何落实在教学过程中.

4.1 宏观分析活动过程

“数学活动”教学，一般是给定真实情境，引导学生用数学的眼光审视、思考情境与哪个数学模型具有较高的关联，提出问题，运用数学模型分析和解决问题，要注重“数学”和“活动”的有机统一，利用“活动”促进学生的探索、思考，使思维活动指向发现问题和解决问题，解决了问题，还需要引导学生抽象和反思.

4.2 “数学活动”的教学结构

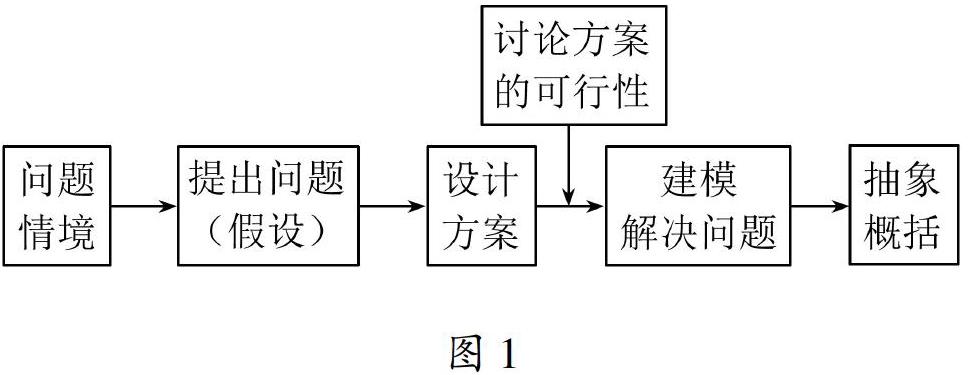
“数学活动”主要有设计、测量、实验探究、调查.根据以上教学过程宏观分析，提出不同类型的“数学活动”教学结构.

规划设计的一种教学结构，如图1.

测量的一种教学结构，如图2.

实验探究类一种教学结构，如图3.

调查类一种教学结构，如图4.

4.3 教学过程设计要点

“数学活动”具有豐富的内涵，独特的活动形式，在促进学生发展等方面，与常规数学课侧重点有所不同，形成互补关系，能够有效培养学生的应用、创新能力，是育人的重要载体，教学过程应关注：

1.重视提出问题.“数学活动”重要价值就在于其实践性的情境能够激发学生的好奇心，易产生问题，因此要尊重学生的主体性，让学生充分经历和体验，从数学的视角提出问题，并尝试解决问题.问题具有衍生性和讨论性，分析、解决问题过程中会不断提出新的问题，问题意识是创新的基础，创新能力会得到培养.

2.重视问题解决过程.“数学活动”关注现实生活，赋予学习意义.要让学生经历观察、思考、合作、修正方案、求解、反思等完整的问题解决活动，注重调动和重组已有经验将实际情境数学化的关键过程，强调在“做”中体验建构，在应用中深化理解数学本质，促进知识的内化、关联和迁移.

3.以评价发挥“数学活动”的育人功能.评价要营造活动的民主氛围，诱导活动兴趣，在丰富的“活动”经历中，获得积极的情感和良好的心理品质，积极的情感才能使学生全身心投入学习.评价要鼓励学生分析问题的创新表现，体现开放性和严谨性的有机统一.要注重表现性评价，怎样的活动才能发展学生的能力和核心素养，表现水平怎样.

4.4 “超市中的数学”教学过程设计

围绕主题“开放几个收款通道”，谈谈教学过程的设计.

这是调查类的“数学活动”，可以根据上面介绍的教学结构展开，其教学组织形式如图5.

1.课前小组调查活动

调查活动分小组实施，小组活动是学习的主阵地.各个小组拟定调查方案，要明确小组成员的职责，共同协作才能提高调研质量.调查的过程和数据可以制成视频和PPT.由于各个小组调查结果的不确定因素，教师也要参与调查，掌握必要的教学资源，充分准备教学预案.

2.小组汇报并构建数学模型解决问题

课上小组汇报调研数据，采取图片、视频和讲解等方式，既能回顾实践体验过程和劳动成果，又能调动课堂气氛，提高学生应用信息技术的能力.然后选取数学模型分析数据，体验从数据到模型解释的过程，提高数据处理能力.

课前拟定调查方案中，学生提出：开设几个通道，关键需要了解结账的速度.但各人结账速度不同，为此，建议对实际情境理想化思考，以便学习探索情境的数学问题.将购物分为购物较少、购物较多两种情况进行统计调查.

汇报一 统计部分顾客结账时间，然后取其平均值得到两种购物的结账速度，也有认为取中位数作为结账速度.

经历这个统计活动，培养学生的信息收集和处理能力，巩固相关统计学概念.知道了结账速度，还要鼓励学生进一步提出问题.汇报二 经小组讨论，需要观察两个通道的数据：A通道购物少的8人，购物多的7人，14.5分钟结算完成;B通道购物少的11人，购物多的5人，13分钟结算完成.

提出问题1：两种情况平均结算时间多长？

这个问题学生建立方程组模型，很快求出购物较少、购物较多平均用时分别为0.5分钟、1.5分钟.

应用题是根据已知条件列方程（组）解决问题，这个解决情境中的问题是应用题的逆向思考.需要自己探索平均结算时间与哪些量高度关联，需要一定的逆向思维能力和创新能力.这样的问题解决会对方程的本质得到较为深刻的理解和再建构.

怎样解决开放几个结账通道的问题呢？根据调查，有的希望通过时间不超过15分钟，也有表示不愿意等待，……

为此，提出问题2：在问题1的前提下，若顾客希望排队和结账时间不超过15分钟，超市什么情况下需要增开收款通道？

分析：设某一时刻购物较少、购物较多的顾客分别有m、n人，若对一个通道而言，要增开通道，则

0.5m+1.5n>15，即m+3n>30.

先考虑特殊情形：若全是购物较少的顾客，也就是n=0，则m>30，即当排队人数超过30人时，就需要增开.若全是购物较多的顾客，也就是m=0，则n>10.即当排队人数超过10人时，就需要增开.

一般情形如何解决呢？引发学生深度思维.启发学生考虑数形结合，从函数视角理解m+3n>30，设m+3n=30，则n=-1/3m+10，图象如图6所示，则人数满足直线上方阴影区域内的整数点时，都需要增开收款通道.这个应用环节学生再次感受到数形结合和函数思想的魅力和价值，构建了方程、不等式、函数的联系，形成新的认知结构.重要的是师生的互动，产生了积极的情感，学生的研究意识也得到加强.

由此，超市应根据每个时段的顾客人数、结账时间和顾客愿意等候的时间等因素，通过模型分析可以确定开放几个收款通道.

为了培养学生的逆向思维能力，在问题2的基础上提出问题3：如果超市必须设置三个收款通道，且购物较少与购物较多的顾客比为2∶1.能否确定该超市这时排队结账的顾客数量范围？

分析：由问题2知道，每个队伍最后一名顾客通过时间超过15分钟就需要增开通道.由于现在必须设置三个收款通道，则30<0.5m+1.5n≤45，即60

以上过程充满数学逻辑的分析、综合、归纳、推理，揭示了问题的深层结构，在用数学中提高了学生的分析、解决问题的能力.

汇报三 经过小组讨论知道，队伍消失与已有排队人数，收款通道每分钟结账人数和增加人数有关，假设队伍人数增加速度、兑换速度一定，为此，只要观察多长时间队伍消失.比如，超市某个时段兑换奖品顾客较多，专门开设通道兑换奖品.若干分钟前就开始排队，开放一个通道，20分钟队伍消失;开放两个通道，8分钟队伍消失.提出问题4：开放三个通道，队伍几分钟消失？

三个量未知，而只有两个条件，可以巧妙利用分式进行代数推理解决问题.此环节培养了学生抽象能力和整体思想.通过以上深度思维，培养了抽象、建模等多种能力和素养.

“数学活动”不能仅满足解决问题，还要设“疑”，使问题新颖和开放，通过在不同情境中的数学建模、抽象等探究活动，整合、拓展、提升知识，发展学生的应用意识和能力.解决问题要鼓励学生独立思考基础上的合作学习、质疑学习，做好过程性评价和表现性评价，对反馈的信息要及时调控，高质量落实“数学活动”的目标.

3.形成报告

通过以上问题提出和问题解决，学生对主题问题有了较为深刻的认识，需要自我反思问题的解决过程，形成调查报告.

总之，“数学活动”从学生生活出发，是一种体验课程，问题解决的特例，其教学过程设计应该具有开放性，充满创造性，应当让学生充分观察、体验、猜想、探究、讨论等自主学习，运用数学模型关联数学与现实生活，将抽象的知识用鲜活的实践体现，这是设计好“数学活动”教学的关键要素.

作者简介 顾广林（1964—），男，中小学正高级教师，江苏省特级教师，主要从事初中“数学活动”研究.

帅建卓（1984—），男，一級教师，泰州市教学能手，主要从事初中数学研究.