“植树问题”教学设计
2021-08-09林宏
林宏

[摘 要]以数学课程标准和学情为依据,采用先学后教的教学模式对“植树问题”进行再设计,突出数学思想的渗透,模型的建构和学生数学核心素养的提升。
[关键词]植树问题;数学思想;核心素养
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2021)20-0058-04
【教学内容】 青岛版教材四年级上册“智慧广场”(第106页~第107页)。
【教材分析】
《义务教育数学课程标准(2011年版)》强调:要从学生已有的生活经验出发,让学生亲身经历将实际问题抽象成数学模型,并进行解释与应用的过程。进而使学生获得对数学理解的同时,在思维能力、情感态度与价值观等方面得到进步和发展。根据课程标准的要求,“智慧广场”的教学目标可概括为以下四点:
1.感悟重要的数学思想方法。
2.运用数学的思维方式进行思考,增强分析和解决问题的能力。
3.提高学习数学的兴趣,增强学好数学的信心,养成良好的学习习惯,具有初步的创新意识。
4.在参与观察、猜测、试验、推理等数学活动中发展合情推理能力,感悟演绎推理思想,学会独立思考。
教材编排了“两端都栽时,间隔数和棵树关系”“一端不栽时,间隔数和棵树关系”“ 两端都不栽时,间隔数和棵树关系”三种不同的情况,并以学生比较熟悉的植树活动为线索,让学生选用自己喜欢的方法来探究栽树的棵数与间隔数之间的关系,经历猜想、实验、推理等数学探索过程,并启发学生透过现象发现规律、建立模型,再回归生活,利用规律解决生活中的实际问题。
【学情分析】
四年级学生仍以形象思维为主,但抽象思维能力有了初步的发展,他们具备了一定的分析综合、抽象概括、梳理规律的数学活动经验。“植树问题”放在这个学段,说明其具有很强的探究空间,需要教师的有效引领和学生的自主探究。
【教学目标】
1.经历将实际问题抽象出数学模型的过程,掌握植树问题中棵树与间隔数之间的关系,并能利用这一关系解决简单的实际问题。
2.经历观察、猜测、验证、推理等解决问题的过程,体验数形结合、一一对应、模型思想等数学思想方法。
3.感受数学在日常生活中的广泛应用,体会数学的价值,产生热爱数学的情感。
【教学重点】
引导学生发现棵数与间隔数之间的关系,使学生经历探究过程,建立植树模型。
【教学难点】
理解间隔数与棵数之間的规律并运用规律解决问题。
【教具准备】
课件、自主学习单、学具等。
【教学过程】
一、任务前置,以学定教
课前布置学习任务(学生独立完成):
“植树问题”悦学单
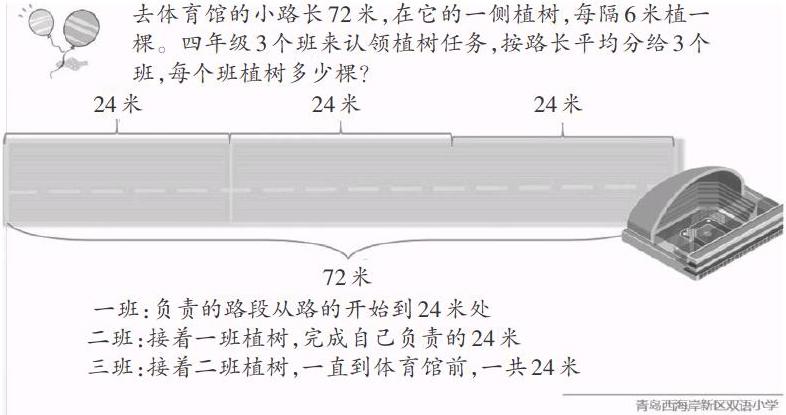
去体育馆的小路长72米,在它的一侧植树,每隔6米植一棵。四年级有3个班认领植树任务,按路长平均分给3个班来完成,每个班负责24米。
一班负责的路段从路的开始到24米处;
二班接着一班植树,完成自己负责的24米;
三班接着二班植树,一直到体育馆前,一共24米。
每个班植树多少棵?
【设计意图:这个环节是由学生课前完成的,能够给学生提供一个自主开放的空间,让学生独立思考问题,从而暴露学生的认知经验和问题。教师就可以发现问题且充分把握学情,确定教学的重难点,体现以学定教。同时,这个情境把植树问题的三种情况都包括在内,是实际生活中的真实情境,不是为了研究而研究,是基于问题解决来研究,有利于学生对知识的建构和理解。“学”在教之前,既实现了“先学后教”,也实现了“悦自主独学”。】
二、小组合作,展示交流
师:昨天大家已经独立研究了植树问题,(板书课题:植树问题)你们认为什么是植树问题?
生1:有关植树的问题就是植树问题。
生2:研究树与间隔的问题就是植树问题。
……
师:那到底是不是你们想的这样呢?今天就一起来研究。根据课件中的图示,请在小组内交流自己的研究成果。
1.一班植树棵数
(1)小组内交流自主学习的成果
师:可以用学具来试着摆一摆,说明一班植树多少棵;也可以用一条线表示小路,用小线段或圆点表示树,画一画,看看一班植树多少棵。
(2) 班内展示小组研究成果
师:请汇报你们的研究成果。
生1:我们开始研究的成果是24÷6=4(棵),也就是看24里面有几个6米,然后通过画线段图、摆小树、交流、讨论,发现一班植树应该是5棵,24÷6=4(棵),4+1=5(棵)。(在黑板上画出线段图表示小路,点上圆点表示树)
生2:我们组也认可这个结论,但是生1没有说清楚为什么加上1棵,谁能讲清楚?
生3:因为从头到尾植树的时候,最后还有一棵树,也就是第一棵树需要第一个空,第二棵树需要第二个空,第三棵树需要第三个空,第四棵树需要第四个空,最后终点还有一棵树,可是没有空了,就把最后的这棵树加上。
师:大家明白生3的讲解吗?数学上称这个空为间隔。那24÷6 表示什么?4指的是什么?为什么+1?
生4:24÷6表示有几个间隔,4是4个间隔,因为4棵树对应4个间隔,最后一棵树没有对应的间隔,所以+1。
师:咱们一致得出结论,一班植树5棵,这是两端植树的情况。因为一棵树对应一个间隔,最后一棵树没有间隔相对应,所以要加上1,这里利用了一一对应的数学思想。(板书:两端植树 一一对应)
2.二班、三班植树棵数
师:我们知道了一班植树的棵数,那二班、三班植树多少棵呢?在小组内继续交流讨论。
生5(在黑板上画图):二班为24÷6=4(棵),因为二班的第一棵树被一班植了,就不用植了,这样一棵树对应一个间隔,有4个间隔,所以植树4棵。
生6:这道题也是利用了一一对应思想。
师:你听得真仔细,还补充了数学思想,非常好。
师:一班是两端植树的情况,那二班是什么情况?
生(齐):一端植树。
师:对,是一端植树的情况。那三班植树多少棵?
生7:三班和二班一样,第一棵树被二班植了,就不用植了,这样一棵树对应一个间隔,有4个间隔,所以植树4棵,列式为24÷6=4(棵)。
生8:我不同意你的说法,三班应该植树3棵,因为最后是体育馆,也不能植树,末尾那棵树不用植,所以是3棵,列式为24÷6-1=3(棵)。
(其他学生都表示同意)
生9:我觉得三班是两端都不植的情况。
师:大家分析得很透彻,有理有据,不仅解决了二班和三班植树棵数的问题,还推理得出二班和三班分别是一端植树和两端不植的情况。
(板书:一端植树 两端不植)。
3.间隔数与棵数之间的关系
师:计算三个班的植树棵数都有算式24÷6,都是先算出4个间隔,然后再+1,或不加不减,或-1,你们发现了什么?请在组内交流一下,然后汇报。
生10:两端都植的情况,总有最后一棵树没有对应的间隔,所以“棵数=间隔数+1”;而一端植树正好是每棵树都对应一个间隔,所以“棵数=间隔数”;而两端都不植的情况就是多了一个间隔,所以“棵数=间隔数-1”。
师:说得很好!发现了规律,表达有逻辑,还总结出了“通过两端都植推理得出一端植树和两端都不植树”的结论。
(板书:棵数=间隔数+1 棵数=间隔数 棵数=间隔数-1 )
【设计意图:对于三个班植树棵数的探究是在互动中完成的,教师给学生创设了宽松的环境,学生在自主独立思考的基础上,通过与组内成员充分交流、大胆发言、探究讨论、畅谈收获、分析辩解,经历了操作、分析、推理、验证、解释、归纳的过程,最后共同解决问题,建构植树问题的模型。因为有和谐的师生关系作为基础,学生乐于展示、乐于分享和上台展示,在互动碰撞中实现对知识的认知、发现、顿悟和对自我的超越,学科素养在潜移默化中逐步提升。这样的教学开启了学生的口,活動了学生的手,也解放了学生的脑,体现了以学为主,真正起到了启发学生智慧,引领学生学习,激发学生兴趣,构建学科知识的作用,学生由“学会”慢慢向“会学”转变,并逐渐“乐学”,真正实现了“和合作群学”。】
三、教师点拨,拓展提升
1.方法提升
师:根据我们总结的规律,可以解决类似的问题,如果只记得其中一种情况,另外两种情况记不住了,怎么能很快知道另外两种情况?
生11:可以通过一种情况推理得出后,只要+1、
+2,或-1、-2就能得出结论。
师:如果三个式子都记不住了,怎么解决呢?
生12:可以通过摆学具或画图的方式发现规律,再利用规律解决问题。
生13:5指4空,可以得到两端都植的结论是“棵数=间隔数+1”;把大拇指去掉,4指4空,可以得到“棵数=间隔数”的结论;再把小手指握住,是3指4空,可以得到“棵数=间隔数-1”的情况。
师:真棒!我们完全可以借助身边的学具和自己的手指,通过操作和探索发现规律,然后利用规律解决问题。这样不仅掌握了知识,更主要的是学会了方法。
(板书:摆、画、手)
2.建立模型
师:刚才我们解决了植树的问题,知道有三种类型,生活中还有类似的现象吗?
师(课件展示军人列队、学生做操站队、公交站示意图、衣服上的纽扣的图片):大家在这里能找到“树”和“间隔”吗?
生14:队伍中的人相当于树,两个人之间的空相当于间隔;公交站牌相当于树,两站之间的距离相当于间隔。
生15:衣服上的纽扣相当于树,两个纽扣间的空相当于间隔,这是一端栽树的情况。
师:大家说的都很到位,这些都是研究“树”与“间隔”之间关系的一类问题,也就是点与线段之间的数量关系,称为植树问题。
【设计意图:有效的教学活动是学生的学与教师的教的统一。教师要发挥主导作用,处理好讲授和学生自主学习的关系。本环节在总结解决植树问题的三种类型规律的基础上,让学生用数学的眼光观察生活,找一找生活中类似植树问题的现象,并思考可以把什么看作“树”,引导学生感悟生活中“模”的存在。学生在已有成果的基础上,进一步提升、拓展,在学习掌握知识的基础上总结方法、积累数学活动经验,由“学会”向“会学”转变,实现了“悦教师引学”,达成了深度学习。】
四、多元测评,展示成果
出示题目:
(1)四年级一班教室在4楼,每层楼有20级台阶,从1楼回教室需要走多少级台阶?
(2)体育馆和图书馆之间相距60米,要在两馆之间的小路两旁摆花盆,相邻两盆花之间的距离是3米,一共要摆多少盆花?
生16:第(1)题中,从1楼走到4楼要走3层台阶,也就是相当于有4棵树、3个间隔,从而列出算式20×(4-1)=60(级)。
师:很好,找准了“树”与“间隔”,并得出是两端都植的情况,从而利用模型解决了问题。
生17:第(2)题是在两馆之间就是说两端都不能摆花,两旁就是要算出两边,所以得出(60÷3-1)×2=38(盆)。
【设计意图:当堂检测是教师了解学生对本节课知识掌握情况的一个重要手段,对教学效果的反馈有着非常重要的作用。在学生理解了植树问题的三种类型后,再让学生独立解决一些数学问题,就能紧扣学习目标,强化学习重点,学生就能充分体验学习的乐趣和获得收获的成就感,实现了“和评价促学”。】
五、拓展延伸,开放教学
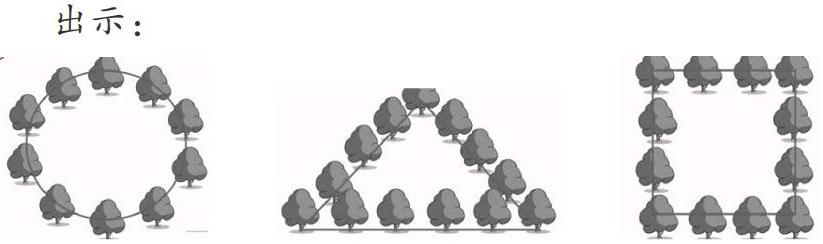
师:这些图中的植树棵数与间隔数之间有什么关系?(动态演示,把封闭图形转化为直线)请课后继续探究。
【设计意图:学生的学习不止于教材,不止于课内,不止于教室内。这样一个环节能帮助学生打开思维,拓展视野,这是开放的学习观,这是一种大学习观,这实现了“悦拓展延学”。】
六、回顾梳理,归纳总结
师:本节课首先是带着学习任务,通过摆学具、画图、交流讨论,得出植树问题的三种情况,通过一一对应、数形结合,大家理解了棵数与间隔数的关系,发现了两端植树情况的规律是“棵数=间隔数+1”,并类比迁移得出一端植树和两端不植情况下的结论,建立了三个模型,并利用模型解决了问题。最后,把封闭图形的植树问题转化为直线上的植树问题,获得了数学方法和思想。(动态出示思维导图)
【设计意图:通过回顾所学知识,学生获得数学知识的同时,获得了数学思想方法,提升了梳理、概括知识的能力。这样能使学生在交流中巩固新知,进一步体会数学与生活的密切联系,真正实现了由双基到四基,由两能到四能的转变,学生的数学素养悄然提升。】
【教学反思】
一、学为中心,以学定教
本节课采用“三环五步五学”的教学模式,凸显“学为中心,以学定教”的生本理念,学生在自主学习的基础上,与同伴共享自学资源,完整经历了研究问题的全过程,学会了学习的方法,实现了由被动学习到主动学习的转化,从而乐学、悦学。
二、追寻有思想的教学
日本教育学者米山国藏说过:“我研究了多年的数学教育,发现学生在初中、高中阶段学习的数学知识离校后不到一两年便很快忘光了,然而,无论他们从事什么工作,唯有深深铭刻于头脑中的数学精神、数学思维方法、研究方法却随时发生作用,使他们受益终身。”顾沛教授指出:“数学思想是数学科学发生、发展的根本,也是数学课程教学的精髓。”依据课程标准的要求,我在这节课中力求凸显数学思想的渗透,追寻有思想的教学。本节课重点突出以下三种思想:
1.一一对应思想
在植树问题教学中,重要的是促进学生从本质上理解模型,因为无论哪种模型,其本质就是一一对应。
2.模型思想
让学生操作学具、画图或用手指研究,自然建立植树问题三种情况的直观模型:加一、不加不减、减一。
列举生活中的摆花、上楼梯等情况,将它们与树的棵数和间隔数进行对比,也就是凸显点与段数之间的对应关系,使学生感受到,虽然情境不同,但都是一类问题,凸显数学模型。
植树问题的模型是现实世界中一类相似事件的放大,它源于生活,卻高于生活。数学思想方法和数学知识相比,知识的有效性是短暂的,思想方法的有效性却是长远的,能够使人受益终身。
3.数形结合思想
数与形反映了事物两个方面的属性。数形结合,主要指的是数与形之间的对应关系,把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,通过“以形助数”或“以数解形”,就能使抽象思维与形象思维相结合。
学生通过摆一摆、画一画,把植树问题中棵数和间隔数之间的关系呈现得一目了然,从而使复杂问题简单化,抽象问题具体化,这样不但起到优化解题途径的作用,也使数学思想方法得到渗透。
(责编 金 铃)
