通过动手操作来探寻植树问题的规律

王柳萍

[摘 要]数学知识可谓是取之于生活，用之于生活，从生产生活中总结抽象出的，最终用来解决生产生活中的相关问题的。让学生参与综合实践活动，在动手操作和体验式探究中感悟数学知识的起源和生成过程，认真观察、动脑思考，理论结合实际，手脑并用，实践与理论循环印证，有利于学生透彻理解知识本质，融会贯通，形成扎实过硬的学习技能。

[关键词]动手操作;植树问题;间隔数

[中圖分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）20-0037-02

教学中，一部分教师舍不得放手让学生去开展活动，深入体验，观察生活现象，并带着疑问和目的去动手操作，再动脑反思其中的奥秘和道理，而是将现成的结论教给学生，强制学生机械记忆和模仿练习，然后打出练习“组合拳”，以期达到理解、巩固知识的目的。这样做，无法启迪智慧，也严重阻遏了学生思维品质的提升，扼杀了学生创新精神的萌发。下面，笔者以人教版教材五年级上册 “植树问题”教学为例，引导学生动手操作，帮助学生探寻规律，让学生从中感悟数学知识的起源和生成过程，从而透彻理解知识本质，融会贯通，形成扎实过硬的学习技能。

一、动手操作参与实践活动，创设情境揭示规律

设计一：参与实践活动

【例1】学校门口有一条6米长的鹅卵石小路，一边要植上棕榈树，每隔2米植一棵（两端都要植），需要几棵棕榈树？（教师用课件展示）

师：请小组合作探究，并交流讨论。

（学生积极思索，热烈讨论，小组发言人代表发言）

组1：我们小组列式6÷2=3，故需要3棵棕榈树。

师：组1的答案是否正确？（赞成者有之，反对者有之，各执一词，相持不下）

组2：我们组的意见是需要4棵棕榈树，但不会列算式。

师：既然众说纷纭，无法统一，那么我们就做一次场景还原，模拟实验，亲自动手勘验测量，用事实说话，孰是孰非，到时自见分晓。

（让学生装扮成棕榈树，用列队方式模拟植树。教室的地板砖为正方形，每块的边长是1米，教室的宽正好是6米，每隔2米站一人，排头排尾各站一人，分别代表两个端点植树，看一共站了几名学生。）

（学生非常主动，排好队后，认真观察和清点人数：发现队伍里站了4人。

师：组2的答案正确，是怎么回事呢？怎么列式？

课件播放还原植树情境（如图1）：

填空：6米长的鹅卵石小路的一边，每隔2米植一棵棕榈树，有________段间隔，一共要植________棵树，按这种算法，植树的棵数比间隔的段数________。（学生迅速填完空，找到解题方法，并且从中总结出规律）

师：本题中，鹅卵石小路的一边两端要植树，故植树的棵数比间隔的段数多1，本题算式为6÷2+1=4（棵）。

我们总说，分析解决问题时要化繁为简，化难为易，也就是运用转化思想将复杂的问题简单化，但是，即使是最简单的基础模型，也要通过操作活动才能深刻地揭露其中的规律，然后将这个规律作为特殊案例，通过合情推理推广到一般情况，最后归纳出解决这类问题的一般法则。如先让学生通过排队的方式直观感知在两端都站人的情况下，站队人数比间隔数多1，然后通过课件展示，得出类似的规律：两端都植树的情况下，3段间隔可以植树4棵。

二、动手画图，融会贯通发展变式

设计二：动手画线段图

【例2】一根角铁长10米，工人师傅要用手锯把它平均锯成5段，每锯断一次耗时8分钟，工人师傅锯完这根角铁需要多久？（教师用课件展示）

师：大家在草稿本上画线段图来演示锯角铁的过程，小组合作探究。

组1：我们小组认为，10米长的角铁，平均锯成5段，除去两头，还有4个切口，因此需要锯4次（如图2），每锯一次用8分钟，因此，算式为（5-1）×8=32（分钟），故锯完这根角铁一共要花32分钟。

师：这一做法正确吗？

生（齐）：对。

师：组1回答得非常正确，算理也解释得非常清楚。这充分表明，大家动手画线段图时真正做到动脑思考，用心揣摩。

植树问题只是一个通用模型，如果按照集合映射的理论来考虑，就会得到很多变式：如“锯木头问题”，锯开的次数与锯成的段数相差1;“上楼梯问题”，楼层号与爬升楼梯的层数相差1;“敲钟问题”，钟声敲响的次数与停顿次数相差1;“结绳问题”，绳子打结个数与绳子分段数相差1……这些都是植树问题的变式，虽然形式各异，但是反映的都是两个相关变量（植树棵数与间隔段数）的“非一一对应关系”，其中一个量随着另一个量等差递增时，始终保持恒定为1的级差。

三、积极思考，合理猜测促使问题顺利解决

设计三：动脑思考，积极猜想

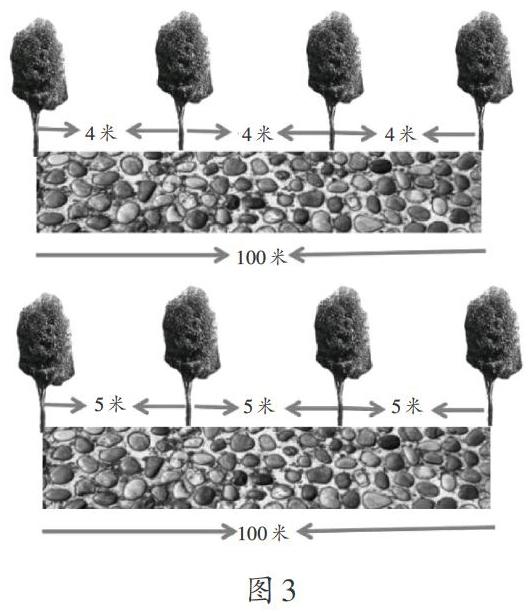
【例3】在一条长100米的鹅卵石小路一边植树（两头都植），原来每4米栽一棵女贞树，现改为每隔5米栽一棵女贞树，共有（ ）棵女贞树不必移栽。

A.4 B.5  C.6  D.7

师（用课件展示图3）：请根据前面学过的方法和总结的规律，开动脑筋、细心推算，小组合作交流。

组1：鹅卵石小路两头的女贞树不必移栽，因为每隔20米处原来的女贞树和现在的女贞树重合，因此从任意一头算起（不算两端），在20米处、40米处、60米处、80米处共4处女贞树重合，再加上两头的2棵树，共有6棵树不必移栽（如图4），故选C。

师：非常好，思路清晰，分析到位，其他同学的结论怎么样？

组2：因为算重合的女贞树时，要从一头算起，所以原来栽种的女贞树为（一头除外）100÷4=25（棵），现在栽种的女贞树为（一头除外）100÷5=20（棵），重合的女贞树数量为25-20+1=6（棵），故选C。

师：有理有据，分析精到。说明同学们做了独立思考，有了自己的主见，通过动手操作、合作探究，将难题破解，值得褒奖。

【例4】圆形水池的周长是150米，如果沿着这水池内圈一周每隔15米安装一个喷头，一共需要安装几个喷头？（教师用课件展示）

师：通过前期的研究学习，同学们对植树问题有了深刻而清醒的认识，本题属于植树问题中的圆形路线植树的变式，同学们仍然可以采取图示法或者假想推演法完成。

生1：我采用的是图示法，把150米的圆周平均分成10份，这样一来就出现10个等分点，每个等分点处安装一个喷头，一共就要安装10个喷头，所列算式是150÷15=10（个），一共需要安装10个喷头。

师：非常正确。还有其他方法吗？

生2：圆周上等距（优弧和劣弧等长）的两点可以将圆周切成等长的两段，等距的三点则能切成等长的三段，同理，等距的10点则能将圆周切成等长的10段，这样把周长为150米的圆形水池切成等长的10段，正好每隔15米安装一个喷头。算式为150÷15=10（个），一共需要安装10个喷头。

师：说得真精彩！算理揭示得一清二楚。

师（总结）：通过动手操作、细心观察、认真思考、合理猜想等，大家都熟练掌握了解决植树问题的各种技巧。其实解决植树问题是有规律可循的，这就需要我们一步步去揭晓其规律。

核心素养反映小学数学教学的魂，教师应在传授数学知识和技能的同时，注重培养学生的数学核心素养。数学核心素养的培养离不开教学的引导者——教师，离不开具体的教学内容和教学过程，离不开教学活动的评价体系。因此只有在具体的数学教学中，重视核心素养、围绕核心素养设计教学活动，带领学生参与丰富多彩的数学实践活动，使学生在实践中长知识、长才干，学会解决生活中的数学问题。

（责编 黄春香）